Анизотропия механических свойств кристалла целекоксиба: природа и особенности с позиций моделирования одноосных деформаций

Ранее было обнаружено [1], что полиморфная форма III (пространственная группа симметрии P– 1) кристалла целекоксиба или 4-[5-(4-метилфенил)-3-(трифторметил)-пиразол-1-ил]бензолсульфонамида является первой из ряда фармпрепаратов, кристаллы которого проявляют исключительные эластичные свойства. Целекосиб (рис. 1) – это селективный нестероидный противовоспалительный препарат. Авторами был проведен эксперимент по изгибу и сдавливанию для количественного определения упругих свойств данного кристаллического материала.

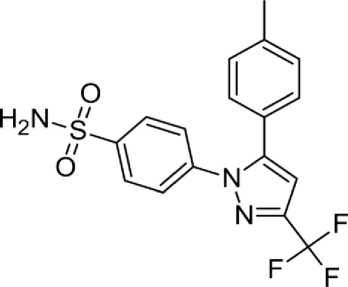
Рис. 1. Структурная формула целекосиба

Авторы синтезов данных кристаллов сообщают о получении игольчатой формы, 3…5 мм в длину и 0,05…0,1 мм в ширину при медленном испарении растворителя из раствора целекокси-ба в метаноле при комнатной температуре [1]. Определённые кристаллографические данные представлены в файле базы CSD с рефкодом DIBBUL01. При анализе данной структуры было установлено [1], что 4-метилфенильные и трифторметильные-1Н-пиразольные кольца расположены примерно в одной плоскости и приблизительно ортогональны бензолсульфоноамидному кольцу. Аминогруппа бензолсульфонамида молекулы целекоксиба связана с атомом азота пиразола другой молекулы, благодаря чему образуется димер, связанный сильной водородной связью. Сам димер ориентируется вдоль оси а, образуя одномерную цепь, которая образована водород- ными связями N–H...O, C–H...N и взаимодействиями C–H...π. Соседние одномерные цепи соединены несколькими слабыми межмолекулярными взаимодействиями C–H...F.

Кристалл имеет замкнутую изотропную упаковку без плоскостей скольжения. Кроме того, в кристалле имеются множественные дисперсионные взаимодействия в ортогональных направлениях, способствующие восстановлению разрывающихся при упругом изгибе других межмолекулярных взаимодействий.

Экспериментально авторами [1] было получено, что целекоксиб легко и многократно подвергается сгибанию при наложении нагрузки вдоль основной грани кристалла (001)/(00-1). При релаксации после снятия нагрузки кристалл возвращается в исходное состояние. Возможность заметного и обратимого изгиба объяснили наличием большого числа слабых водородных связей между димерами целекосиба, которые усиливаются сильными водородными связями внутри димера. Однако при наложении напряжения сгиба вдоль малой грани (0-11)/(01-1) кристалл разрушался еще до того, как деформация стала заметной. Отсюда был сделан вывод, что кристалл це-лекоксиба является одномерным эластичным кристаллом при деформации только по одной грани, а наличие набора сильных и слабых межмолекулярных связей может определять высокую эластичность кристаллов.

В нашей работе были поставлены следующие задачи:

• –    проведение виртуального теста растяжения кристаллической структуры целекоксиба, выявление причин различающегося динамического механического поведения (эластич-ность/пластичность/хрупкость) в разных направлениях на основе анализа структурных изменений, конфигурации и свойств нековалентных связей и цепей, а также энергии и объёма элементарной ячейки при последовательных шагах растяжения;

• –    изучение особенностей ориентации нековалентных взаимодействий и построенных на них кристаллических мотивов (цепей) в равновесной форме кристаллов целекоксиба;

• –    оценка влияния нековалентных связей и кристаллических цепей на сопротивление внешним деформациям путем анализа пространственных зависимостей модулей упругости равновесной формы кристаллов в сопоставлении с анизотропной ориентацией этих структурных элементов.

Экспериментальная часть

Для структуры кристалла целекоксиба были проведены расчёты методами Кона – Шэма (DFT) и Хартри – Фока (с дисперсионными поправками) с периодическими граничными условиями, при использовании пакета программ CRYSTAL17 (v.1.0.2). Начальные данные взяты из экспериментального cif-файла с рефкодом базы CSD DIBBUL01, приложенного к статье [1]. Расчеты проводились на уровнях HF3c/MINIX и PBE0/pob-DZVP2. Сначала выполнялась полная оптимизация координат атомов и параметров кристаллографической ячейки с сохранением пространственной группы, то есть с релаксацией координат атомов и параметров ячейки. При этом использовались следующие параметры сходимости: по энергии в SCF-цикле 10–10 aт. ед., по градиенту 10–5 aт. ед. и по смещению 3·10–5 aт. ед. Затем к оптимизированным структурам применялся алгоритм расчёта тензора жесткости, изложенный в [2] (опция ELASTCON программы CRYSTAL17) с параметрами сходимости: по энергии в SCF-цикле 10–8 aт. ед., по градиенту 5·10–5 aт. ед. и по смещению 10–4 aт. ед. Далее в работе был использован онлайн-инструмент ELATE [3] и код Cryst-Compress [4], чтобы получить значения объемных модулей для расчёта индексов анизотропии AU [5] и AL [6], собственные значения тензора и пространственные зависимости модулей упругости с информацией о минимальных и максимальных значениях модулей Юнга, линейной сжимаемости, а также декартовых осях их ориентации. С помощью инструмента CrystCompress получены данные по всем осям максимальных и минимальных значений модуля Юнга и линейной сжимаемости, а также пространственные зависимости обратных им модулей – одноосной сжимаемости и гидростатической жёсткости. Все структуры показали положительные собственные значения тензора жёсткости, что соответствует критерию устойчивости структур.

С помощью программы ToposPro [7] и её функции AutoCN были найдены все нековалентные контакты в кристаллической ячейке, отвечающие геометрическим критериям нековалентных связей. Использованные параметры программы: для водородных связей – установленные по умолчанию – r(H…Y) = 3.00; r(X…Y) = 4.00; ∠XHY = 90º; для остальных нековалентных связей – r(X…Y) = 4.00; ∠XHY = 75.0º; omega (X…B)= 5.0. При использовании функции IsoCryst была визуализирована кристаллическая ячейка и нековалентные контакты в пространстве ячейки. Для определения того, являются ли атомы в найденных контактах действительно взаимодействующими, волновые функции оптимизированных структур были проанализированы на предмет наличия связевых критических точек электронной плотности (3, –1) найденных контактов. Взаимодействия со значением электронной плотности в связевых критических точках (ρ(rbcp)) менее 0.002 ат.ед. были исключены из дальнейшего рассмотрения, как оказывающие незначительное влияние на пространственную картину механических свойств. Анализ критических точек и определение значения электронной плотности в них, ρ(rbcp), были выполнены с помощью инструмента TOPOND14, входящего в состав программы CRYSTAL17.

Для упрощения кристаллических структур с целью определения построенных на межмолекулярных нековалентных связях кристаллических цепей использовалась программа ToposPro и ее функция ADS. Нами применялся стандартный метод упрощения структур, содержащих валентные, водородные и другие специфические межатомные связи. Для этого сначала рассчитывается матрица смежности через использование функции AutoCN. В процессе упрощения структуры использовались настройки ADS по умолчанию: Common Flags – Save Simplified Net; Simplification Method – Standard; Bond Types Valence – At.; H bonds – Mol. При использовании функции IsoCryst были визуализированы кристаллические ячейки с полученными цепями и проанализировано, на каких последовательностях молекул и межмолекулярных связей строятся данные цепи. Визуальное представление фрагментов кристаллических структур осуществлялось с помощью программного пакета Chemcraft [8]. С помощью его функции «Add custom vectors and planes» были построены соответствующие оси максимумов и минимумов модуля Юнга и линейной сжимаемости, вычисленные при анализе тензора жёсткости. После построения осей были найдены значения углов между направлениями нековалентных связей и осей крайних значений модулей упругости.

Виртуальный тест растяжения кристаллических структур проводился по алгоритму, представленному А.Э. Масуновым и др. в [9]. Для фиксации определённой деформации кристалла по трем осям a , b и c , по отдельности, применялись опции CRYDEF и FIXDEF программы CRYSTAL17, с сохранением пространственной группы и всех операторов симметрии. Эти параметры позволили провести оптимизацию координат атомов и параметров кристаллической ячейки, когда один из этих параметров сохранялся постоянным во время оптимизации. Чтобы смоделировать деформацию растяжения, бралась предварительно полностью оптимизированная, с указанными выше параметрами, равновесная кристаллическая структура, один из параметров ячейки увеличивался (уменьшался) на 3 % и фиксировался при оптимизации новой, растянутой (сжатой) структуры. После того, как остальные параметры ячейки и координаты атомов были релаксированы, величина этого параметра увеличивалась (уменьшалась) ещё на 3 % относительно начальной (равновесной) величины и вновь фиксировалась, далее проводилась новая оптимизация. Эта пошаговая оптимизация повторялась десять раз, до 30 % удлинения (укорочения) кристалла по одной из осей. Далее были построены зависимости изменения объёма и полной энергии кристаллографической ячейки от процента изменения каждого параметра, и проанализированы изменения конфигурации межмолекулярных связей и структурных особенностей полученных кристаллических форм.

Обсуждение результатов

Анализ тензора жесткости кристалла целекоксиба.

При анализе рассчитанных на двух уровнях PBE0/pob-DZVP2 и HF3c/MINIX тензоров жесткости были получены данные по пространственным зависимостям модуля Юнга и линейной сжимаемости для кристалла целекоксиба (табл. 1), а также рассчитаны его усреднённые модули упругости (табл. 2), универсальный и логарифмический индексы упругой анизотропии (табл. 3). Так как полученные данные различаются в небольшой степени, для существенного сокращения необходимых компьютерных ресурсов и времени, виртуальный тест растяжения проведён на уровне HF3c/MINIX.

Таблица 1

Рассчитанные значения упругих модулей и их анизотропии для кристалла целекоксиба

Способ расчета	Модуль Юнга, ГПа				Линейная сжимаемость, ТПа–1				Модуль сдвига
	min		max		β min		β max		G min	G max
PBE0/ pob-DZVP2	6,7		23,3		8,4		48,2		2,6	9,7
HF3c/MINIX	7,1		31,2		14,3		46,9		2,7	10,1
Значение вдоль оси	a	b		c	a	b		c	–
PBE0/ pob-DZVP2	12,4	9,4		16,6	26,7	35,5		25,1	–
HF3c/MINIX	10,8	8,2		16,4	24,4	30,6		33,4
Уровень расчета	Анизотропия модуля Юнга				Анизотропия линейной сжимаемости				Анизотропия модуля сдвига
PBE0/ pob-DZVP2	3,50				5,71				3,70
HF3c/MINIX	4,39				3,28				3,68
Пространственные оси крайних значений модулей
PBE0/pob-DZVP	E min		max		β min		β max		G min	G max
x	0,715		–0,111		–0,665		0,630		0,470	–0,671
y	0,325		0,183		0,059		0,580		0,872	0,425
z	0,619		0,977		0,744		0,516		–0,137	0,608
HF3c/MINIX	min		max		β min		β max		G min	G max
x	–0,052		–0,774		0,660		0,472		–0,673	–0,621
y	–0,938		0,632		–0,721		0,616		–0,723	0,459
z	–0,343		–0,042		0,211		0,631		–0,129	0,636

Таблица 2

Усредненные значения модулей упругости для кристалла целекоксиба

Усреднение	PBE0/pob-DZVP2			HF3c/MINIX
	Объемный модуль K, ГПа	Модуль Юнга E, ГПа	Модуль сдвига G, ГПа	Объемный модуль K, ГПа	Модуль Юнга E, ГПа	Модуль сдвига G, ГПа
По Фойгту	12,9	14,4	5,5	12,9	15,5	5,9
По Ройсу	12,1	10,8	4,0	11,9	11,6	4,4
По Хиллу	12,5	12,6	4,7	12,4	13,6	5,2

Таблица 3

Индексы упругой анизотропии для целекоксиба

Форма	Универсальный индекс анизотропии, AU	Логарифмический индекс анизотропии, AL
PBE0/pob-DZVP2	1,96	1,61
HF3c/MINIX	1,92	1,56

Исходя из табл. 1, величина модуля Юнга относительно средняя для молекулярных кристаллов, в том числе, его максимальное значение, равное 31,2 ГПа. Поэтому по одному параметру сложно сделать вывод о мягкости/жёсткости кристалла целекоксиба. Величины индексов упругой анизотропии имеют невысокие значения, но они больше единицы, что указывает на некоторую вероятность проявления гибкости кристаллом целекоксиба. Для него были определены оси максимального и минимального значений модуля Юнга и линейной сжимаемости, пространственные зависимости которых изображены на рис. 2. Пространственная зависимость модуля Юнга относительно фрагментов структуры целекоксиба изображена на рис. 3.

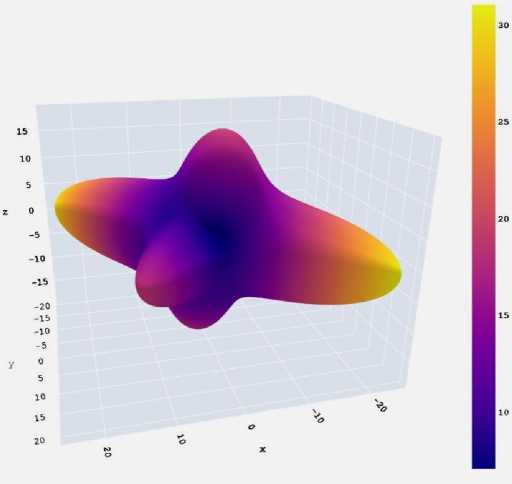
a)

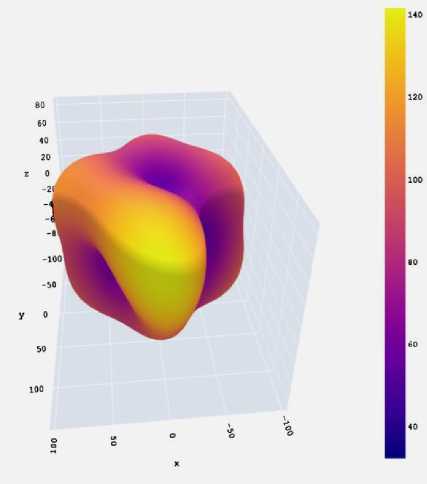
b)

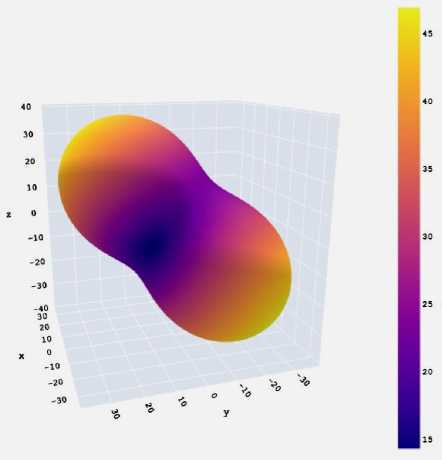
с)

Рис. 2. Трехмерные пространственные зависимости в кристалле целекоксиба: а – для модуля Юнга (в ГПа); b – одноосной сжимаемости (в ТПа–1);

с – линейной сжимаемости (в ТПа–1); d – гидростатической сжимаемости (в ГПа)

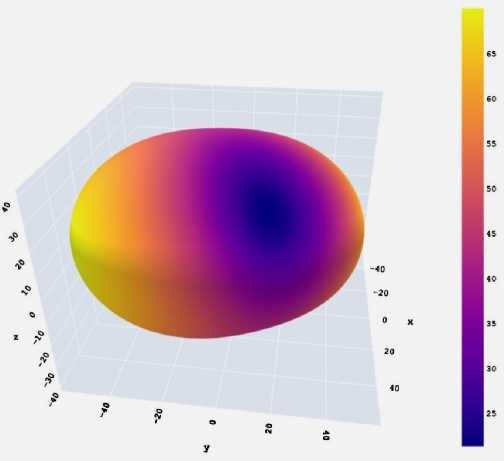
d)

Всего в кристаллической ячейке целекоксиба было определено присутствие 9 нековалентных связей (табл. 4), согласно наличию связевых путей в электронной плотности. Найденные связи показаны на рис. 4 . Из полученных результатов можно сказать, что сильная водородная связь H₁…O₂ вносит наибольший вклад в сопротивление внешнему одноосному напряжению и значение анизотропии модуля Юнга, так как ортогональна оси минимума и образует угол 51º с осью максимума модуля Юнга. Данная связь является основой прямой цепи вдоль оси а кристаллографической ячейки, которая параллельна оси а и ортогональна (табл. 5) другим осям (рис. 5). Данная цепь также была определена ранее авторами [1]. По значению электронной плотности в критической точке связи (ρ( r bcp ) = 0,026 ат. ед.) можно сказать, что эта цепь должна быть относительно прочной.

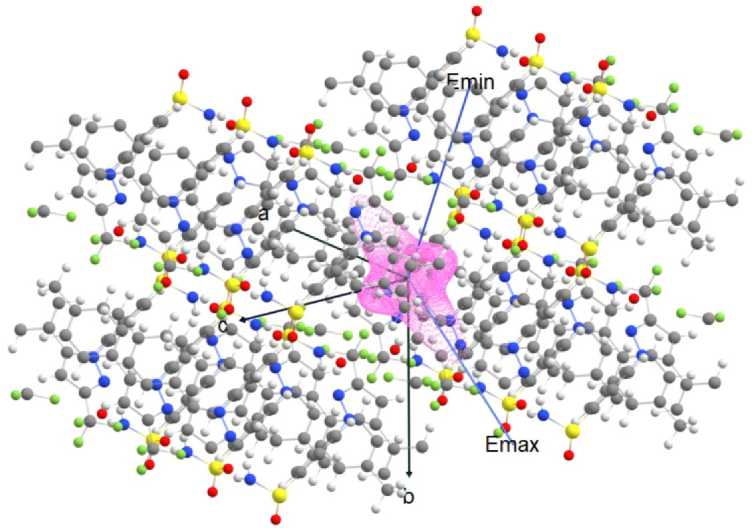
Рис. 3. Пространственная зависимость модуля Юнга относительно фрагмента кристаллической структуры целекоксиба

Косвенно на прочность цепи указывает факт, что она образует относительно большой угол с направлением максимального значения линейной сжимаемости. Однако по значению модуля Юнга, равному 10,8 ГПа вдоль оси а , мы можем говорить о податливости данной цепи, поскольку сопротивление вдоль неё близко к минимальному значению модуля Юнга. Другая сильная водородная связь, H 3 …N 1 , формирует димерные фрагменты целекоксиба, и это вносит существенный вклад в сопротивление гидростатическому напряжению, так как угол между данной связью и осью максимума линейной сжимаемости большой, а угол между ней и осью минимума линейной сжимаемости – минимальный (8º).

Таблица 4 Нековалентные межмолекулярные связи в кристалле целекоксиба и их минимальные углы с осями крайних значений модулей упругости

Связь	Длина связи, Å	Длина связи эксп., Å	ρ( r bcp ) ат. ед.	Угол между связью и Emin	Угол между связью и Е™™ и max	Угол между связью и β min	Угол между связью и β max
H 1 …O 2	1,914	2,087	0,026	90	51	63	75
H 2 …F 2	2,468	2,588	0,003	71	85	85	58
H 3 …N 1	2,034	2,187	0,024	52	60	8	77
H 5 …N 3	2,664	2,736	0,006	18	64	66	26
H 6 …F 3	2,627	2,810	0,004	45	72	79	38
H 9 …F 1	2,521	2,586	0,005	26	36	40	54
H 12 …O 1	2,385	2,560	0,010	70	74	85	67
H 13 …N 1	2,543	2,740	0,008	71	54	54	36
O 1 …O 1	3,115	3,459	0,005	77	63	56	45

Таблица 5

Значения минимальных углов между молекулярной цепью целекоксиба и модулями упругости

a	b	c	min	max	β min	β max
0	90	90	87	39	49	62

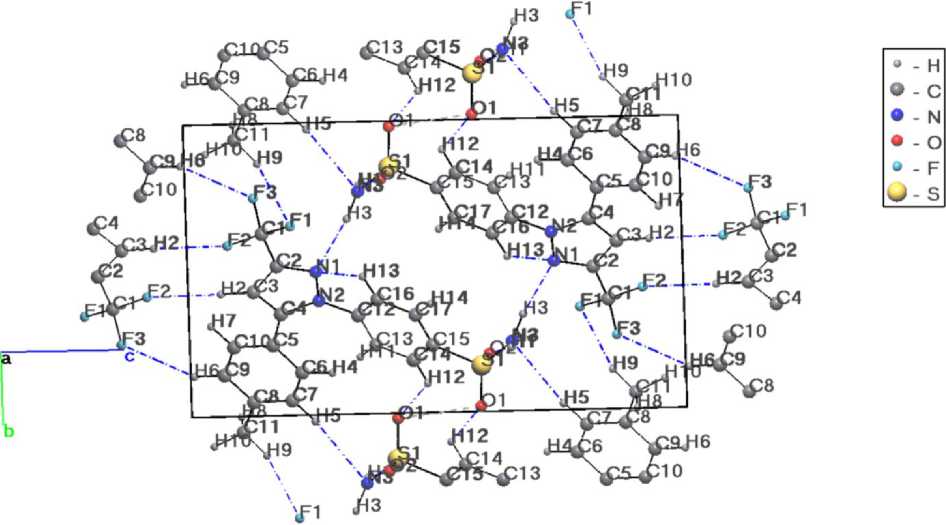
Рис. 4. Межмолекулярные нековалентные связи в кристалле целекоксиба

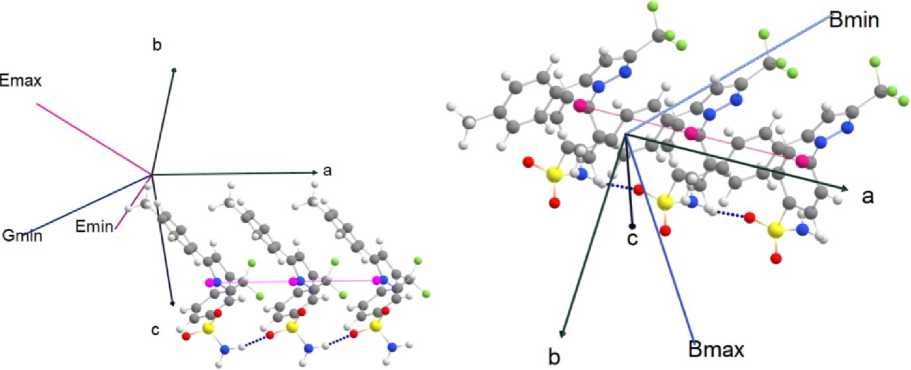
a)                                                                b)

Рис. 5. Молекулярная цепь в кристалле целекоксиба (розовым цветом отмечены центры масс молекул-звеньев цепи) относительно направления крайних значений (a) модуля Юнга (b) линейной сжимаемости

Связи разной силы (ρ( r bcp ) = 0.005…0.026 ат. ед.), например, H 1 …O 2 , H 3 …N 1 , O 1 …O 1 , H₁₂…O₁, и некоторые другие практически не влияют на минимальное значение модуля Юнга, так как углы (рис. 6) между данными связями и осью минимума модуля Юнга относительно велики, а связь H 5 …N 3 , наоборот, способствует некоторому увеличению этого значения. На максимальное значение модуля Юнга наибольшим образом влияют водородные связи – H₉…F₁ и в некоторой степени H 1 …O 2 . В целом можно сделать вывод, что максимальное значение модуля Юнга будет определять скорее молекулярная цепь, так как она образует угол с его осью меньший, чем соответствующие углы с отдельно взятыми водородными связями.

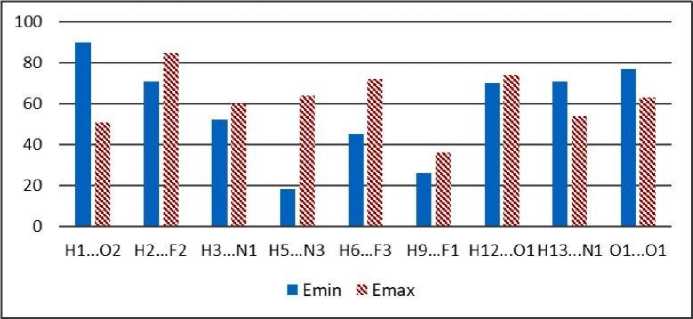
Рис. 6. Гистограмма распределения минимальных углов нековалентных межмолекулярных связей с пространственными осями значений модуля Юнга для кристалла целекоксиба

Характеристики нековалентных связей, структурные изменения и механическое поведение при виртуальном тесте растяжения кристалла целекоксиба

Мы проанализировали результаты виртуального теста растяжения кристалла целекоксиба вдоль каждой из трёх кристаллографических осей. Из приведённых в табл. 6 данных можно отметить, что при растяжении кристалла вдоль кристаллографической оси a сильная водородная связь H 1 …O 2 перестает наблюдаться уже на шаге растяжения 15 %. Это связано с тем, что данная связь ориентирована ближе к направлению приложенной деформации, поэтому её длина быстро увеличивается при росте растяжения. При разрыве этой связи образуется локальная полость, вытянутая вдоль кристаллографической оси b , которая при дальнейшем увеличении деформации не заполняется новыми нековалентными взаимодействиями. Изменение энергии кристаллической ячейки, связанное с исчезновением связевого пути, возможно, компенсируется в этом случае изменениями связи H 2 …F 2 , которая в испытанном диапазоне растяжения усиливается. Поэтому при росте растяжения изменение энергии ячейки относительно монотонно растёт, не вызывая появление экстремумов на графике (рис. 7) и не выходя на горизонтальное плато.

Таблица 6

Изменение длины связей кристалла целекоксиба при растяжении вдоль оси а

Связь/шаг	0 %	3 %	6 %	9 %	12 %	15 %	18 %	21 %	24 %	27 %	30 %
H 1 …O 2	1,914	2,002	2,136	2,299	2,489	–	–	–	–	–	–
H 3 …N 1	2,034	2,021	2,012	2,006	2,001	1,999	1,997	1,997	2,005	2,033	2,075
H 12 …O 1	2,385	2,416	2,447	2,483	2,528	2,568	2,669	2,757	2,743	2,704	2,659
H 13 …N 1	2,543	2,562	–	–	–	–	–	–	–	–	–
O 1 …O 1	3,115	3,123	3,121	3,118	3,118	3,098	–	–	–	–	–
H 5 …N 3	2,664	2,647	2,640	2,638	2,641	2,638	2,641	2,646	2,633	2,632	2,607
H 6 …F 3	2,627	2,598	2,557	2,536	–	–	–	–	–	–	–
H 2 …F 2	2,468	2,473	2,477	2,479	2,460	2,433	2,376	2,321	2,294	2,295	2,318
H 9 …F 1	2,521	2,558	2,596	2,645	2,698	2,775	2,881	2,993	–	–	–

Мы можем отметить два возможных варианта поведения кристалла при деформации. С одной стороны, во всем диапазоне растяжения вдоль оси а рост энергии самый существенный относительно изменения энергии при растяжении вдоль других осей, что указывает на высокое сопротивление кристалла внешнему напряжению и поэтому скорее эластичный характер механического поведения при деформации вдоль оси а . Четыре связи, в том числе связь H 3 …N 1 , образующая димеры молекулы, наблюдаются во всем испытанном диапазоне деформации, то есть они сопротивляются разрыву даже на большом шаге растяжения (30 %), а исчезновение других связей практически не влияет на изменение энергии ячейки, что также может указывать на эластичный характер поведения. Полученные результаты соответствуют данным эксперимента об эластичном характере кристалла при изгибе вдоль грани (001), то есть кристаллографической плоскости a0b . Однако, с другой стороны, может реализоваться и другой вариант механического поведения, поскольку одна из сильных связей разрывается при росте растяжения, и формируется незарастающая полость.

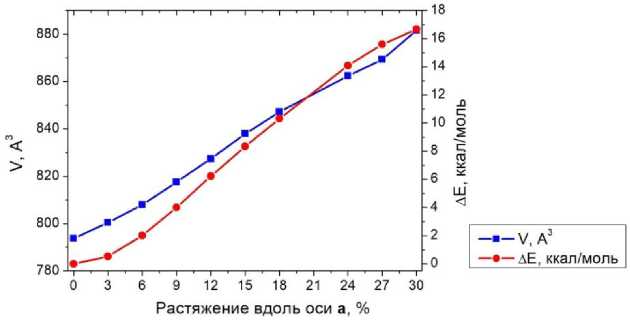
Рис. 7. Характеристики кристалла целекоксиба при виртуальном растяжении вдоль оси а

То есть возможно достижение предела эластичности на шаге ~15 %, появление трещины и проявление хрупкости данным кристаллом при высоких значениях растяжения, несмотря на тренд изменения энергии ячейки. Этот факт согласуется с экспериментальными наблюдениями при изгибе кристалла вдоль грани (0-11)/(01-1), то есть вдоль кристаллографической оси a [1], когда происходило разрушение кристалла.

Поскольку из-за морфологических особенностей особое внимание уделяется поведению кристалла при механическом воздействии вдоль кристаллографической оси а , то формально в кристалле целекоксиба нами выделено две подгруппы связей согласно их поведению именно при растяжении вдоль оси a . Так, связи H₁…O₂ и H₆…F₃, H₁₃…N₁, O₁…O₁, H₉…F₁ можно отнести к первой подгруппе. При растяжении данные связи сначала увеличивают свою длину, а затем происходит их разрыв, что, скорее всего, связано с их ориентацией близко к направлению растяжения (рис. 8а). Несмотря на то, что связь O 1 …O 1 на первых шагах растяжения сохраняет свою длину, но на шаге 15 % происходит её разрыв, поэтому она отнесена также к первой подгруппе. Ко второй подгруппе можно отнести связи H 3 …N 1 , H 5 …N 3 , H 2 …F 2 и H 12 …O 1 , так как они существуют во всем испытанном диапазоне растяжения и изменяются при растяжении незначительно. График изменения длины связей данной подгруппы представлен на рис. 8b.

b)

a)

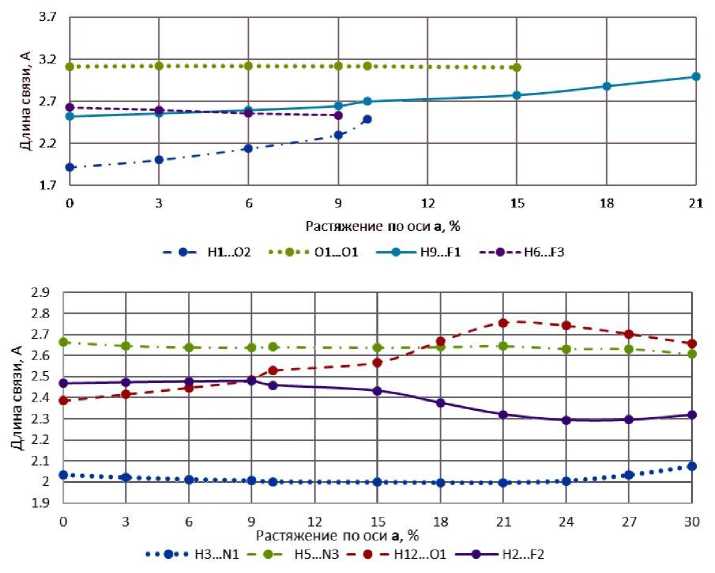
Рис. 8. Изменение длины связей: а) первой подгруппы, b) второй подгруппы в кристалле целекоксиба при растяжении вдоль оси a

При растяжении структуры целекоксиба вдоль кристаллографической оси b на графике изменения энергии и объема относительно равновесной структуры от процента растяжения (рис. 9) наблюдается появление локального максимума при 15–18 % растяжении. Этот максимум можно связать, в первую очередь, с началом роста длины сильной связи H 1 …O 2 (табл. 7), что сопровождается компенсирующим уменьшением длины, иными словами усилением прочности, связей H₅…N₃, H₁₂…O₁, O₁…O₁ и H₂…F₂. Возможно, сопротивление именно этих слабых связей приводит к резкому, но небольшому по абсолютной величине, снижению тренда в диапазоне растяжения более 18 %. Кроме этого, на шаге 15 % растяжения связи H 3 …N 1 , H 9 …F 1 перестают наблюдаться и разрываются, то есть исчезает связь, формирующая молекулярные димеры. Более слабая связь H₁₃…N₁ разрывается на меньшем шаге растяжения. Поскольку в процессе оптимизации параметр b приблизился вплотную к величине, соответствующей шагу 24 , то шаг растяжения 21 % отсутствует. Указанный выше разрыв связей и перестройка структуры приводят к уменьшению изменения энергии относительно равновесной с выходом на низкое плато, кристалл перестает сопротивляться внешнему напряжению и показывает уже скорее пластичные свойства, с формированием новой и усилением существующих связей (см. табл. 7). Мы видим, что крутизна графика изменения энергии при растяжении вдоль осей a и b практически одинакова до шага 15 %, а при большей деформации во втором случае происходит значимое изменение кристаллической структуры. Показанный тренд не противоречит эластичному поведению кристалла до шага растяжения 15 % по обеим осям, что согласуется с экспериментальными данными [1] о возможности обратимого изгиба вдоль грани (001), то есть плоскости a0b .

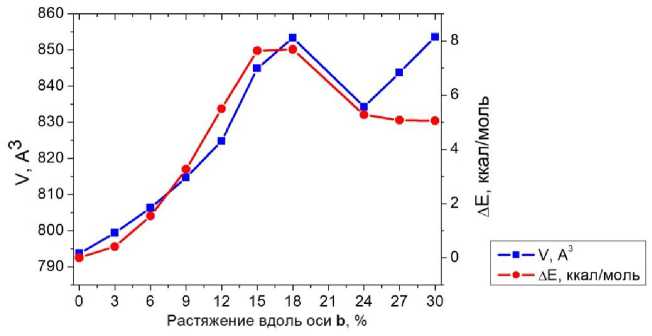
Рис. 9. Характеристики кристалла целекоксиба при виртуальном растяжении вдоль оси b

Таблица 7

Изменение длины связей кристалла целекоксиба при растяжении вдоль оси b

Связь/шаг	0 %	3 %	6 %	9 %	12 %	15 %	18 %	24 %	27 %	30 %
H 1 …O 2	1,914	1,898	1,892	1,895	1,896	1,878	1,902	2,135	2,121	2,084
H 3 …N 1	2,034	2,073	2,127	2,201	2,326	–	–	–	–	–
H 5 …N 3	2,664	2,683	2,714	2,748	2,753	2,536	2,393	2,632	2,629	2,607
H 12 …O 1	2,385	2,385	2,408	2,440	2,464	2,275	2,126	2,024	2,029	2,035
H 13 …N 1	2,543	2,577	2,613	–	–	–	–	–	–	–
O 1 …O 1	3,115	3,129	3,177	3,237	3,262	2,992	2,799	2,813	2,812	2,813
H 6 …F 3	2,627	2,670	2,703	2,736	2,760	2,904	–	–	–	–
H 9 …F 1	2,521	2,564	2,610	2,662	2,724	–	–	–	–	–
H 2 …F 2	2,468	2,461	2,458	2,453	2,446	2,408	2,412	2,366	2,378	2,393
H 3 …F 1	–	–	2,848	2,795	2,752	2,871	2,523	2,440	2,474	2,507
H 14 …F 3	–	–	–	–	–	–	–	2,568	2,493	2,453

При растяжении кристалла целекоксиба вдоль оси с наблюдается постепенное увеличение расстояния между фрагментами молекул, а именно плоскостями пиразольного и метилбензольного колец, чего не происходит при растяжении вдоль других осей. В процессе роста деформации данное явление приводит к появлению трещины вдоль всего кристалла на шаге 27 % растяжения, вытянутой вдоль кристаллографической оси b (рис. 10). То есть, по данному направлению проявляются явно хрупкие свойства кристалла при высоком значении растяжения. С этим также согласуется факт, что на зависимости изменения энергии от величины растяжения можно увидеть, что в диапазоне 27–30 % изменение энергии становится несколько меньше, начинает проявляться возможный выход на плато (рис. 11), а объём ячейки, наоборот, скачкообразно увеличивается.

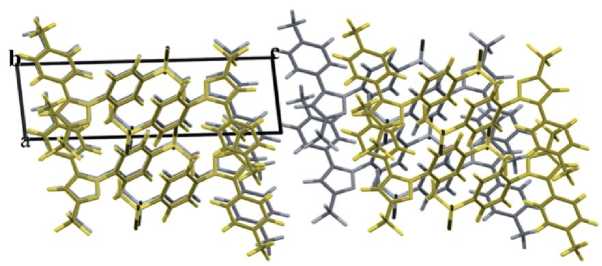
Рис. 10. Различие растянутой вдоль оси с на шаге 3 % структуры кристалла целекоксиба (серый цвет) со структурой при растяжении вдоль оси с на шаге 27 % (желтый цвет)

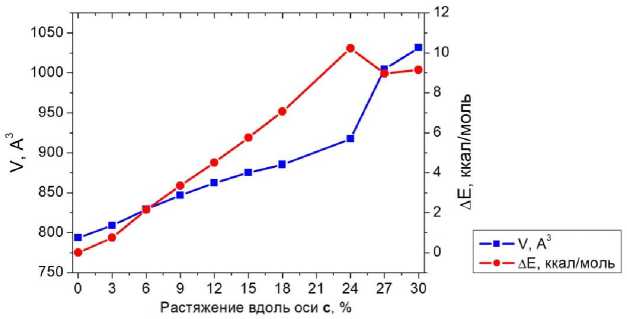
Рис. 11. Характеристики кристалла целекоксиба при виртуальном растяжении вдоль оси с

По изменению набора связей в ходе растяжения в данном направлении трудно оценить, появляется ли трещина, поскольку ещё на начальных этапах растяжения перестают наблюдаться только слабые связи H 5 …N 3 , H 6 …F 3 , H 9 …F 1 (табл. 8). Однако о возможном образовании трещины можно судить по резкому увеличению длин связей H₁…O₂, H₂…F₂, H₁₃…N₁ при 27 % растяжении, а в особенности связи H₁₂…O₁, которая во всем испытанном диапазоне усиливалась с уменьшением длины, но при 27 % резко ослабевает. Данный факт был отмечен (см. выше по тексту) при визуальном анализе структуры.

Таблица 8

Изменение длины связей кристалла целекоксиба при растяжении вдоль оси с

Связь/шаг	0 %	3 %	6 %	9 %	12 %	15 %	18 %	21 %	24 %	27 %	30 %
H 1 …O 2	1,914	1,915	1,922	1,915	1,910	1,906	1,899	1,895	1,898	1,917	1,918
H 2 …F 2	2,468	2,721	2,949	2,938	2,928	2,920	2,916	2,910	2,907	2,960	2,962
H 3 …N 1	2,034	2,054	2,050	2,054	2,058	2,062	2,069	2,082	2,079	2,051	2,048
H 5 …N 3	2,664	2,876	–	–	–	–	–	–	–	2,621	2,620
H 6 …F 3	2,627	2,800	–	–	–	–	–	–	–	–	–
H 9 …F 1	2,521	2,515	2,791	–	–	–	–	–	–	–	–
H 12 …O 1	2,385	2,361	2,267	2,214	2,179	2,154	2,137	2,134	2,134	2,418	2,419
H 13 …N 1	2,543	2,525	2,518	2,505	2,489	2,474	2,459	2,441	2,439	2,580	2,580
O 1 …O 1	3,115	3,068	2,887	2,803	2,753	2,718	2,696	2,686	2,686	3,170	3,168

Выводы

Исходя из теоретического анализа тензора жесткости целекоксиба, можно сделать следующие выводы. Для прогноза механических свойств кристалла целекоксиба недостаточно использовать только характеристики, полученные из тензора жесткости, поскольку они не подтверждают однозначно конкретные свойства кристалла. Значения индексов анизотропии упругости указывают на возможную гибкость целекоксиба. О вероятной гибкости кристалла мы можем также судить по ориентации оси измерения минимального значения модуля сдвига, которая почти параллельна плоскости a 0 b , то есть (001). Если рассматривать значения модуля Юнга по пространственным направлениям, то в направлении оси с это значение больше (16,4 ГПа), чем в направлениях осей a (10,8 ГПа) и b (8,2 ГПа). Поэтому можно утверждать, что кристалл целекоксиба нельзя считать мягким. Следует отметить, что рассчитанное на двух уровнях теории значение модуля Юнга практически совпадает с экспериментальным значением модуля Юнга для грани (001), то есть вдоль оси c – 16,27 ГПа, полученным методом наноиндентации [1]. Ориентация оси максимального значения модуля Юнга, с одной стороны, не совпадает с направлениями как молекулярной цепи, так и сильных водородных связей. Но, с другой стороны, это направление достаточно близко к плоскости фенильного и пиразоль-ного колец молекулы целекоксиба, то есть причиной максимального сопротивления одноосной деформации может быть жёсткость из-за ориентации ароматических колец.

По результатам виртуального теста на растяжение кристалла целекоксиба можно отметить, что теоретический анализ поведения нековалентных связей при проведении теста подтверждает экспериментально наблюдаемые характерные особенности различающегося поведения эластичных, пластичных и хрупких кристаллов при растяжении [9, 10]. Полученные результаты также соответствуют экспериментальным наблюдениям [1], что кристалл может проявлять эластичные свойства вдоль кристаллографической плоскости а0b наряду с явной хрупкостью вдоль оси a , в то время как вдоль оси с кристалл не может быть эластичным.