Аномалии эфемеридных и временных продуктов IGS и их влияние на решение навигационных задач

Задача высокоточного позиционирования (precise point positioning, PPP) имеет большое значение в геодезии и является одним из способов использования глобальных спутниковых навигационных систем (ГНСС). Для решения такой задачи используются фазовые и кодовые измерения с навигационного приемника, а также уточненная информация об орбитах и часах навигационных спутников. В качестве источника информации об уточненных (финальных) орбитах и часах (частотно-временных поправках к шкале времени спутника) выступают аналитические центры Международной службы ГНСС (IGS) [1]: ИАЦ ГЛОНАСС [2], CODE [3], ESA [4] и др. Информация об орбитах передается в формате SP3 на каждый суточный интервал времени в виде временных рядов данных с шагом по времени 15 мин [5], информация о часах спутника передается в формате CLK с шагом по времени 30 с или 5 мин [6]. Используемый нами метод обнаружения аномалий в орбитах ранее был подробно описан в работах [7; 8] и позволяет обнаруживать малые (сантиметровые) аномалии в орбитах навигационных спутников. Также в работе [7] отмечается, что на стыках суточных интервалах в орбитах часто присутствуют разрывы («скачки»). Обнаружение аномалий в уходах часов не представляет труда: достаточно удалить линейные и квадратичные (для больших временных интервалов) тренды методом наименьших квадратов (МНК).

Нами были предприняты попытки «исправить» обнаруженные аномалии орбит, т. е. скорректировать орбиту так, чтобы новая орбита не имела бы разрыва на стыке суток и была близка к опубликованным финальным орбитам. Однако такая коррекция не всегда приводила к повышению точности позиционирования либо ее ухудшала. Это связано с наличием подобных аномалий и во временной информации (уход часов НКА).

Метод обнаружения аномалий орбит

Методика поиска аномалий в SP3-данных (стандартный текстовый формат для эфемеридных продуктов IGS, доступны суточными интервалами с шагом 15 мин по времени) состоит в поиске разрывов орбиты (скачков временного ряда) на стыке двух суточных интервалов путем аппроксимации каждой из координат спутника для этого двухсуточного интервала полиномом высокой степени. Далее вычисляется невязка аппроксимации. Как показано в [7; 8], по полученной невязке легко определить тип аномалии («скачок» или «выброс», а также маневр спутника или период вхождения в тень). Применявшийся нами метод аппроксимации основан на использовании предвычисляемого набора дискретных ортогональных полиномов Чебышева– Хана [8]. Такие полиномы рассчитываются в метках времени анализируемого ряда до выбранной степени r (в нашем случае r = 100) , после чего легко вычисляется полином наилучшего среднеквадратичного приближения. Основная проблема состоит в вычислении полиномов Чебышева–Хана. Стандартные формулы теории ортогональных дискретных полиномов непригодны в силу накопления большой ошибки для высоких степеней и при большом количестве точек (в нашем случае 192 точки). Устойчивые алгоритмы вычисления полиномов Чебышева– Хана описаны в [8]. В данной работе мы использовали программный комплекс [9], адаптированный к задаче аппроксимации орбит. Метод полиномиальной аппроксимации существенно проще рассматривавшегося ранее в [10; 11] подхода, предусматривавшего высокоточное моделирование движения НКА с помощью решения уравнений движения с использованием множества дополнительных данных.

Для решаемых нами задач точного позиционирования важна аномалия орбиты не по каждой отдельной координате, а величина ее проекции на ось визирования между спутником и приемником. Для упрощения анализа в качестве координат приемника использовался центр масс Земли, т. е. вычислялась величина аномалии вдоль радиус-вектора НКА – центр Земли.

Аномалии, обнаруженные в финальных орбитах IGS

Вопрос аномалий в орбитах навигационных спутников обсуждается в работах [7; 8; 10; 11]. В работе [7] показаны обнаруженные аномалии в орбитах спутников ГЛОНАСС; такие же аномалии наблюдаются и в орбитах спутников GPS. Примеры обнаруженных «скачков» в финальных орбитах спутников G03 и G08 на стыке суток (точнее, их воздействие на невязки аппроксимации) по данным аналитического центра ИАЦ КВНО, показаны на рис. 1 и 2.

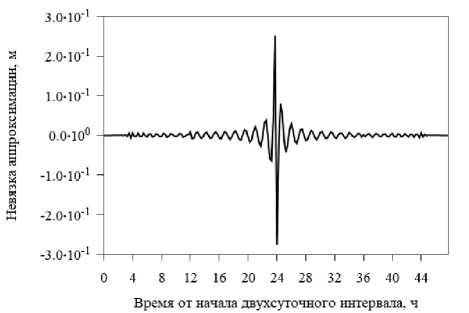
Рис. 1. Невязка аппроксимации полиномом степени 100 координаты Y спутника G03 на стыке суток 21–22 ноября 2014 г. ИАЦ КВНО

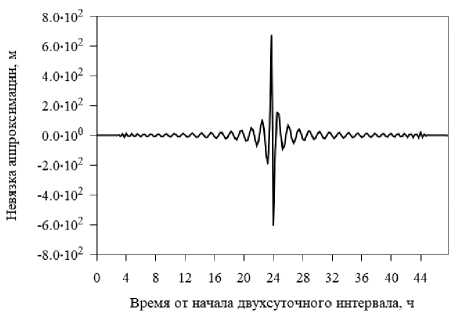
Рис. 2. Невязка аппроксимации полиномом степени 100 координаты Y спутника G08 на стыке суток 5–6 апреля 2018 г. ИАЦ КВНО

Fig. 1. Residual of approximation by a polynomial of degree 100 of the Y coordinate of the G03 satellite at the day boundary 21–22 November 2014 by the IAC PNT

Fig. 2. Residual of approximation by a polynomial of degree 100 of the Y coordinate of the G08 satellite at the day boundary 5–6 April 2018 by the IAC PNT

Согласно рекомендациям, приведенным в работе [7], определим величину «скачка» на каждом из стыков суток. Для невязки аппроксимации, изображенной на рис. 1, величина «скачка» составляет около 70 см, для невязки аппроксимации на рис. 2 величина «скачка» составляет около 1,8 км. Большие «скачки» в финальных орбитах аналитических центров встречаются не очень часто (в среднем 1 «скачок» в год для каждого спутника), тогда как маленькие «скачки» встречаются часто.

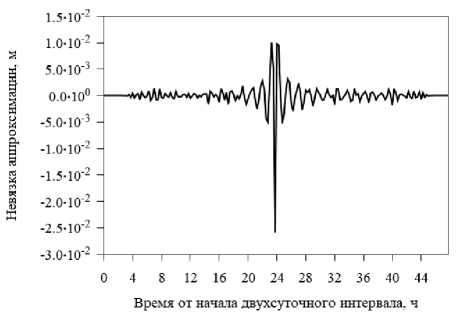
Рис. 3. Невязка аппроксимации полиномом степени 100 координаты Y спутника G04 на стыке суток («выброс») 22–23 мая 2016 г. ИАЦ КВНО

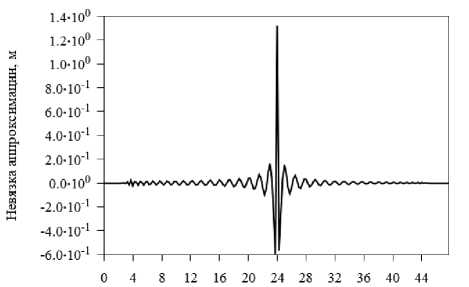
Время от начала двухсуточного интервала, ч

Рис. 4. Невязка аппроксимации полиномом степени 100 координаты Y спутника G01 на стыке суток («выброс») 7–8 ноября 2016 г. ИАЦ КВНО

Fig. 3. Residual of approximation by a polynomial of degree 100 of the Y coordinate of the G04 satellite at the day boundary 22–23 May 2016 by the IAC PNT

Fig. 4. Residual of approximation by a polynomial of degree 100 of the Y coordinate of the G01 satellite at the day boundary 7–8 November 2016 by the IAC PNT

Помимо «скачков», в финальных орбитах спутников GPS наблюдались и «выбросы». На рис. 3 и 4 показаны «выбросы» в финальных орбитах спутников GPS G01 и G04 соответственно (точнее, как и ранее для «скачков», воздействие «выбросов» на невязки аппроксимации).

Величина «выброса» в орбите спутника G04 (рис. 3), определенного по невязке аппроксимации, составляет приблизительно 3,5 см. В орбите спутника G01 (рис. 4) величина «выброса» составляет примерно 1,8 м.

Следующей аномалией, которую позволяет обнаружить данная методика - поведение финальной орбиты навигационного спутника при выполнении маневра. Подтвердить присутствие маневра у спутника GPS возможно, используя сообщения NANU (Notice Advisory to Navstar Users) [12; 13]. Спутник G15, согласно сообщениям NANU, выполнял один из маневров 20 августа 2013 г. Рассмотрим невязку аппроксимации координаты X полиномом 100 степени финальной орбиты данного спутника за 20–21 августа 2013 г. (рис. 5).

Согласно данным NANU, маневр спутника начался в 13:01 GPS Time и закончился в 19:42 GPS Time. Из временной диаграммы невязки на рис. 3 видно, что на середину этого участка приходится пик в невязке аппроксимации орбиты спутника. Отметим отличие в форме (растянутость по временной оси) аномалий невязок для рис. 3–5.

По невязкам результатов аппроксимации можно определить участки вхождения в тень, временная диаграмма невязки для такой ситуации представлена на рис. 6. Для подтверждения вхождения в тень был определен угол СОЗ (Солнце – Объект – Земля), который соответствовал на данном временном интервале присутствию теневых участков орбиты.

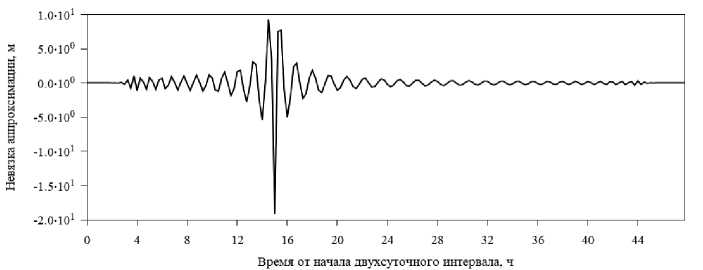
Рис. 5. Невязка аппроксимации полиномом степени 100 «маневра» координата X спутника G15 на стыке суток 20–21 августа 2013 г. ИАЦ КВНО

Fig. 5. Residual of approximation by a polynomial of degree 100 of the X coordinate of the G15 satellite at the day boundary 20–21 August 2013 by the IAC PNT

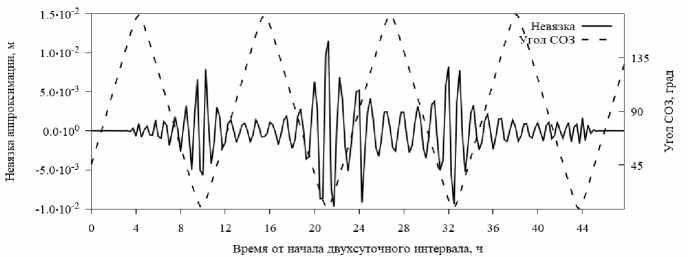
Рис. 6. Временные диаграммы невязки аппроксимации для спутника R03 для временного интервала 30–31 мая 2013 г.

Fig. 6. Residual of approximation by a polynomial of degree 100 of the X coordinate of the R03 satellite at the day boundary 30–31 May 2013 by the IAC PNT and angle SOE

В дальнейшем при накоплении статистики аномалий у различных аналитических центров мы будем рассматривать максимум модуля невязки (для каждого спутника берется максимальное значение из трех координат).

Статистика аномалий в финальных орбитах GPS

В работе [7] приведена статистика аномалий в финальных орбитах различных аналитических центров для спутников ГЛОНАСС. В данном разделе показана статистика аномалий для спутников GPS с 2010 по 2018 гг.

Разделим найденные максимумы модуля невязки (по всем трем координатам) на 2 группы: менее 10 и более 10 см.

Для группы, где величина менее 10 см, построим двумерное распределение, где в качестве одного из измерений выбираем спутник, к которому относится максимум модуля невязки на каждом двухсуточном интервале (начало интервала берется в начале каждых суток), в качестве второго – величину этого максимума модуля невязки с шагом 1 см. Накопление количества аномалий выполняется на всем временном интервале (с 2010 по 2018 г.), по каждому аналитическому центру графики строятся отдельно. Двумерные гистограммы для каждого аналитического центра представлены: на рис. 7 для CODE, на рис. 8 для ESA, на рис. 9 для ИАЦ КВНО, на рис. 10 для IGS. Справа от гистограммы показана легенда количества аномалий с 2010 по 2018 гг.

Для группы менее 10 см можно отметить, что финальные орбиты различных аналитических центров имеют различное количество аномалий, превышающих 1 см. Аналитический центр CODE имеет не более 120 аномалий на 1 спутник в диапазоне от 1 до 2 см. Аналитический центр ESA имеет в среднем от 1500 до 1800 аномалий в диапазоне от 1 до 2 см на каждый спутник. Аналитический центр ИАЦ КВНО имеет в среднем от 1000 до 1400 аномалий в диапазоне от 1 до 2 см на каждый спутник. Аналитический центр IGS имеет в среднем от 400 до 900 аномалий в диапазоне от 1 до 2 см на каждый спутник. При этом можно увидеть взаимосвязь в количестве аномалий на спутник между аналитическими центрами CODE и IGS.

Ситуаций, когда максимум модуля невязки превышает порог в 10 см, значительно меньше, для таких ситуаций также построим двумерное распределение. В качестве одного из измерений выбираем спутник, а в качестве второго - начало годичного интервала (с шагом 1 год). За каждый год накапливается число аномалий с максимумом модуля невязки более 10 см на всех двухсуточных интервалах аппроксимации, по каждому аналитическому центру отдельно. Полученные распределения показаны на рис. 11 для CODE, 12 – ESA, 13 – ИАЦ КВНО, 14 – IGS. Справа от гистограммы показана легенда количества событий.

Наиболее значимые аномалии, имеющие массовый характер (почти для всех НКА), наблюдались у аналитического центра ИАЦ КВНО в 2014 и 2016 гг. Для разных аналитических центров можно отметить, что наблюдались годы, когда для определенных спутников достигалось максимальное для данного центра количество аномалий в год. При этом такие ситуации не всегда взаимосвязаны у различных центров. Это частично объясняется, в том числе, и пропусками в публикуемых каждым центром SP3-данных (когда центр не выкладывал недостоверные с его точки зрения орбиты): сутки с большими аномалиями для одного центра могли быть просто выброшены другим центром и не присутствуют тем самым в статистике на рис. 11–14. Доступность (наличие на серверах IGS) SP3-данных для аналитического центра CODE составляет 97 %, ESA – 90 %, ИАЦ КВНО – 93 %, IGS – 95 %. В среднем по всем аналитическим центрам максимальное число аномалий, превышающих 10 см, не более 20.

G01 G02 GO3 GO4 GOS GO6 GO7 GOS G09 GIO Gil G12 G13 G14 G15 G16 G17 G1S G19 G20 G21 G22 G23 G24 G25 G26 G27 G28 G29 G3O G31 G32 Спутник

Рис. 7. Распределение количества аномалий менее 10 см за интервал наблюдения с 2010 по 2018 гг. для аналитического центра CODE

• Fig. 7.    Distribution of the number of anomalies less than 10 cm over the observation interval from 2010 to 2018 for the CODE analytical center

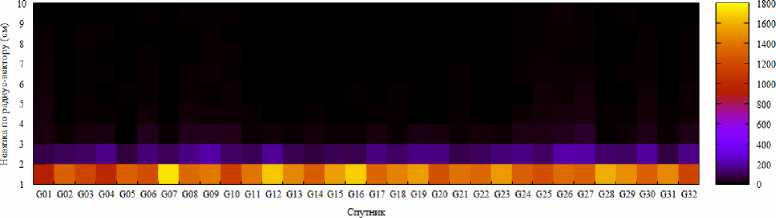
Рис. 8. Распределение количества аномалии менее 10 см за интервал наблюдения с 2010 по 2018 гг. для аналитического центра ESA

• Fig. 8.    Distribution of the number of anomalies less than 10 cm over the observation interval from 2010 to 2018 for the ESA analytical center

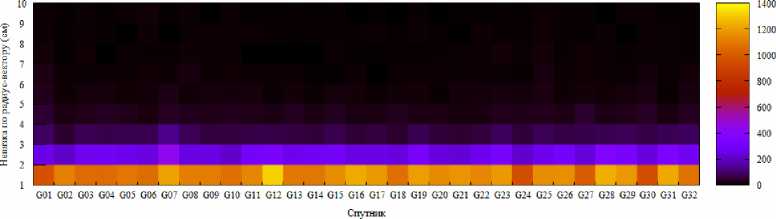
Рис. 9. Распределение количества аномалии менее 10 см за интервал наблюдения с 2010 по 2018 гг. для аналитического центра ИАЦ

• Fig. 9.    Distribution of the number of anomalies less than 10 cm over the observation interval from 2010 to 2018 for the analytical center of the IAC KVNO

Рис. 10. Распределение количества аномалии менее 10 см за интервал наблюдения с 2010 по 2018 гг. для аналитического центра IGS

Fig. 10. Distribution of the number of anomalies less than 10 cm over the observation interval from 2010 to 2018 for the IGS analytical center

mw.t;

GO! G02 G03 G04 G05 G06 G07 GOS G0 9 GIO Gil G12 G13 G14 G15 G16 G17 GIB G19 G20 G21 G22 G23 G24 G2 5 G26 G2 7 G2S G29 G3 0 G31 G32 Спутник

Рис. 11. Распределение аномалий более 10 см по годам для аналитического центра CODE

Fig. 11. Distribution of anomalies over 10 cm by year for the CODE analytical center

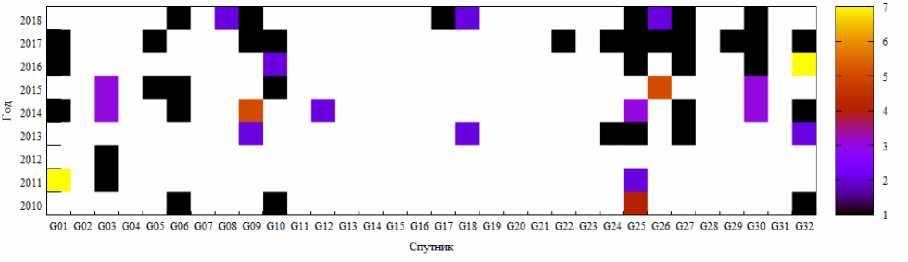
Рис. 12. Распределение аномалий более 10 см по годам для аналитического центра ESA

Fig. 12. Distribution of anomalies over 10 cm by year for the ESA analytical center

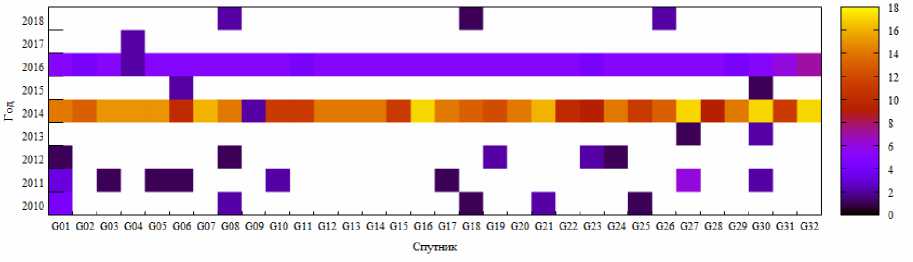
Рис. 13. Распределение аномалий более 10 см по годам для аналитического центра ИАЦ

Fig. 13. Distribution of anomalies over 10 cm by years for the analytical center IAC KVNO

Рис. 14. Распределение аномалий более 10 см по годам для аналитического центра IGS

Fig. 14. Distribution of anomalies over 10 cm by year for the IGS analytical center

Был выполнен анализ положения максимума модуля невязки в окне аппроксимации. Чаще всего максимум приходился на стык суточных интервалов, однако наблюдались ситуации у спутников GPS, когда аномалия приходилась не на стык суточных интервалов, что почти всегда было связано с маневрами спутников GPS.

Как видно из гистограмм, у всех аналитических центров встречаются как большие (более 10 см), так и малые (менее 10 см) аномалии в финальных орбитах, которые тем не менее предлагается использовать в задачах высокоточного позиционирования.

Аномалии, обнаруживаемые в уходах часов спутников GPS

Для двухсуточных интервалов на стыках суток, для которых наблюдались аномалии по максимуму модуля невязки, превышающие несколько см (для разных аналитических центров выбирались различные минимальные отклонения), были исследованы уходы часов с удалением линейного (и квадратичного для больших интервалов времени) тренда.

За период с 2010 по 2018 гг. была накоплена статистика разрывов, величина которых по радиус-вектору превышала 5 см. Для спутников GPS в данных аналитического центра CODE таких ситуаций было 42. В данных аналитического центра IGS их было 275, при этом исключались ситуации, когда разрыв превышал по радиус-вектору 10 м. На стыках суток с разрывом в орбите выполнялась аппроксимация уходов часов спутника линейной функцией и вычислялась невязка аппроксимации. Далее проводился совместный анализ невязок аппроксимации орбиты и ухода часов данного НКА. Как оказалось, при решении задачи PPP эти невязки (разрывы данных), как правило, взаимно компенсируются. Типичный пример компенсации разрывов на стыке суток в орбите и уходе часов приведен на рис. 15, 16.

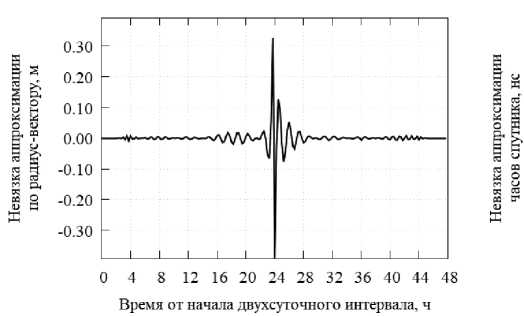
Рис. 15. Невязка аппроксимации расстояния по радиус-вектору полиномом степени 100 орбиты спутника G30 на стыке суток 30 ноября – 1 декабря 2015 г., центр CODE

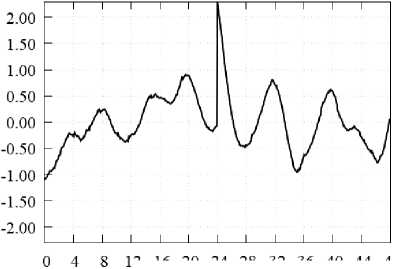
12 16 20 24 28 32 36 40 44 48

Время от начала двухсуточного интервала, ч

Рис. 16. Невязка аппроксимации ухода часов спутника G30 полиномом степени 1 на стыке суток 30 ноября – 1 декабря 2015 г., центр CODE

Fig. 15. Residual of approximation by a polynomial of degree 100 of the radius-vector orbit of the G30 satellite at the day boundary 30 November 2010 – 01 December 2010 by the CODE

Fig. 16. Residual of approximation by a polynomial of degree 1 of the G30 satellite clock at the day boundary 30 November 2010 – 01 December 2010 by the CODE

На рис. 13 разрыв в орбите по радиус-вектору составляет около 60 см, он частично компенсируется при решении задач PPP разрывом в часах (приблизительно 2 нс).

Влияние аномалий в продуктах IGS на решение задачи PPP

Задача высокоточного позиционирования (PPP) заключается в нахождении с сантиметровой точностью координат станции и её ухода часов по прямым измерениям фазы и псевдодально- сти по сигналам НКА. Для решения этой задачи необходимо использовать высокоточные эфемериды и апостериорные оценки ухода часов НКА, которые мы берём из финальных SP3- и RINEX Clock-файлов службы IGS, а также других обрабатывающих центров. Кроме того, согласно [14], для достижения адекватной точности необходим учёт следующих эффектов:

– релятивистская поправка часов [15];

• –    задержка сигнала в тропосфере (при выполнении данной работы используется модель из [15], формула (9.12), при этом параметры D hz , D wz , G N , G E моделируются с помощью кусочнолинейной функции, значения функций в узлах оцениваются вместе с координатами и уходом часов станции);

• –    смещение фазового центра антенн НКА и станций, а также вариация фазового центра в зависимости от угла, под которым передаётся и принимается сигнал по отношению к надиру и зениту, соответственно (эти поправки передаются в файлах ANTEX службой IGS);

• –    поправка на вращения фазы сигнала при повороте НКА относительно приемника;

• –    смещение наземного измерительного пункта за счёт деформаций земной коры, вызванных приливами в твёрдом теле Земли, неравномерностью вращения Земли, а также давлением океанической воды, перемещающейся под действием приливных сил Луны и Солнца [15].

Исходными данными в задаче PPP становятся измерения псевдодальности и фазы по сигналам НКА. Оцениваемыми параметрами являются координаты станции, уход часов приёмника, параметры модели задержки сигнала в тропосфере и фазовая неоднозначность. Модель измерительных данных представляет собой систему условных уравнений, связывающих измеренные и оцениваемые величины. Система решается путём линеаризации по уточняемым параметрам, линейная система решается методом наименьших квадратов.

В работе использовались измерительные данные со станций IGS [1]: KOKV, MGUE, MAD2, HRAO. Для таких станций выбирались дни, когда спутник с аномалией в орбите находился в зоне радиовидимости станции на стыке суток (аномалии определялись полиномиальной аппроксимацией). Было проведено 2 серии экспериментов, в которых оценивались такие параметры, как невязка псевдодальности между измеренной безионосферной комбинацией и смоделированной в задаче PPP, а также координаты станции наблюдения.

В первой серии экспериментов задача PPP решалась на двухсуточных интервалах с аномалией в орбите какого-либо спутника на стыке этих интервалов. В экспериментах прежде всего оценивалось влияние аномалии в орбите спутника на невязки между измеренной безионосфер-ной фазовой псевдодальностью и ее модельным значением. В невязках наблюдались аномальные «скачки», как у спутника с аномалией в орбите, так и у других спутников. На следующем этапе данной серии экспериментов мы исключили из решения задачи PPP спутники с аномалией в орбите. После чего снова проанализировали невязки псевдодальности. В результате аномалии в псевдодальностях вблизи стыка суток уменьшили свою величину или полностью исчезли. На третьем этапе данной серии экспериментов, вместо исключения спутника с аномалией в орбите, мы пытались «исправить» эту аномалию, формируя новую орбиту, используя модель движения спутника, описанную в IERS Conventions [15], согласуя ее с опубликованными финальными орбитами на двухсуточном интервале. Анализ невязок псевдодальности показал, что подобным образом исправленные орбиты не только не уменьшают величину «скачка» или «выброса» невязок, но зачастую приводят к их увеличению. Такая ситуация является следствием того, что в уходах часов спутника тоже присутствуют аномалии, при этом данные аномалии часто компенсируют аномалии в орбитах, поэтому подход, связанный с исправлением только аномалий в орбитах, не может быть применен.

Вторая серия экспериментов была посвящена оценке качества решения задачи PPP на относительно небольшом интервале, который расположен на стыке суток с аномалией. В экспери- ментах рассматривался интервал в 2 часа до и после стыка суток (рис. 17), на котором решалась задача PPP.

момент времени, на который решается задача РРР

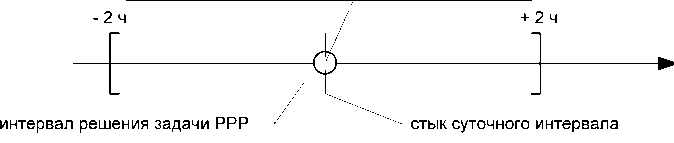
Рис. 17. Временная диаграмма решения задачи PPP во второй серии экспериментов

Fig. 17. Timing diagram of solving the PPP problem in the second series of experiments

Задача PPP тем самым решалась в трех вариантах: а) спутники с аномалией в орбите включались в решение; б) спутники с аномалией исключались из решения; в) для спутников с аномалией исправлялась орбита. В качестве эталонных координат брались координаты станции, полученные осреднением трех решений задачи PPP на двухсуточном интервале: в начале, в середине и в конце. В результате было выявлено, что в большинстве случаев исключение спутника с аномалией в орбите из решения задачи PPP, уменьшает ошибку определения координат. Попытки «исправить» орбиту спутника с аномалией в ней только увеличивают ошибку определения координат.

Для оценки качества решения задачи PPP в данной серии экспериментов также определялась евклидова норма расстояния между тремя осредненными координатами и тремя координатами, определенными в решении задачи PPP, их статистика по всем станциям на всех интервалах решения показана в таблице.

Статистика распределения евклидовой нормы расстояния между осредненными и определенными координатами

	Без аномальных спутников	С аномальными спутниками	Для аномальных спутников проведена корректировка орбиты
Максимальное	151 см	115 см	28088 см
Среднее	37 см	36 см	2682 см
СКО	26 см	21 см	3407 см

Как видно из таблицы, решение без спутников с аномалией в орбите в среднем значении на 1 см хуже решения с аномальным спутником, тогда как решение с корректированной орбитой в среднем хуже на 2682 см.

Заключение

В эфемеридно-временных продуктах аналитических центров ГНСС нередко присутствуют существенные аномалии на стыках суток, что негативно влияет на точность решения навигационных задач. Нами предложена и опробована на 9-летнем временном интервале простая методика нахождения разрывов и других аномалий в публикуемых аналитическими центрами IGS финальных орбитах. Приведенный анализ аномалий показал, что имеет место взаимная компенсация разрывов в орбите и уходе часов спутника при решении задач PPP. Попытки «исправления» орбит с целью удаления разрывов на стыке суток не имеют смысла без соответствующей коррекции уходов часов НКА, что на данном этапе не представляется возможным.