Антагонизм в вариациях солнечной активности

Солнечная цикличность представляет периодические изменения в Солнечной активности (СА) с длительностью около 11 лет [1]. Для объяснения подобной периодичности в возникновении пятен обычно используется теория Солнечного динамо [4].

Активность Солнца подвержена периодическим изменениям, в годы максимума активности Солнце ярче, чем в годы минимума. Некоторые исследователи склоняются к мнению, что основой активности являются внутренние механизмы. Анализ их данных показывает, что в ядре скорость вращения Солнца вокруг своей оси значительно выше, чем на поверхности. А неустойчивость в подавлении турбулентной теплопроводности магнитного поля может служить одним из механизмов формирования Солнечных пятен [3, 4, 11].

Другие исследователи утверждают, что 11 летний цикл и более долговременные циклы, связанные с периодическим пропаданием активности Солнца на период несколько десятков лет, можно объяснить возникновением резонансных влияний центробежных сил, возникающих при эллиптическом движении планет вокруг Солнца. Показано, что возникающие силы гравитации определяются не массой тел, а ускорением вихря среды и суммарной массой элементарных частиц взаимодействующего физического тела [6].

Вторая точка зрения выглядит логичнее. Но, нужно учитывать и то, что планеты вращаются вокруг своей оси, а некоторые имеют один или несколько спутников, которые обращаются вокруг планет. Пояса астероидов и метеоритов так же обращаются вокруг Солнца. Так же Солнечная система обращается вокруг центра галактики, вместе с которой осуществляет свой путь во Вселенной [1]. Весь этот набор центробежных сил, взаимодействуя с общим центром тяжести, вызывает нарушение динамического равновесия, в результате которого проявляется нестабильность процессов Солнечной активности.

Факторы, влияющие на изменение СА в 11-ти летних циклах, безусловно, изменяют и число Солнечных пятен (чисел Вольфа). В динамике временного ряда 11 летнего цикла СА присутствует чередование амплитуд повышенной и пониженной активности, а разница между ними в динамике временного ряда представляет вариабельность ритма активности (рис. 1). Множество факторов внешнего и внутреннего характера влияют на этот ритм [5], вот почему за многовековую историю наблюдения за СА в его цикличности не выявлено схожих форм в тенденциях и формах активности.

Замедление и учащение ритмов активности связывают так же с эпохами «пониженной» и «повышенной» СА. В 11-ти летнем цикле выделяют ветви роста и спа- да СА, которые так же имеют различия. Отмечено, что продолжительность ветвей спада более значительна в динамике большинства циклов [3].

Исследования методом долевых тенденций амплитуд прироста и спада в гармонике временного ряда (ритмах активности) позволили выявить большую СА в ветвях роста, чем в ветвях спада. Причем, в «повышенной» эпохе эта активность выше в два раза, что подтверждает факт повышения нестабильности процессов саморегуляции СА в этот период [8, 9].

Как показывают графики (рис. 1) в ветвях роста и спада ритм СА наблюдается чередование амплитуд. Возможно, эти тенденции характеризуют антагонизм в саморегуляции динамического равновесия.

Ядро – единственное место на Солнце, в котором энергия и тепло получается от термоядерной реакции, остальная же часть звезды нагрета этой энергией. Силами, ре- гулирующими активность термоядерных реакций в ядре Солнца, имеющего наибольшую долю веса, возможно, может выступать взаимодействие планетарных центробежных сил с общим центром тяжести Солнечной системы [6].

В действительности, во всех вращательных движениях центробежная сила первична, вызывая растяжение, упругую деформацию, разрыв или разрушение связей, опор, а центростремительная - есть не что иное как сила реакции этих связей. Итак, центробежная и центростремительная силы обусловлены вихрем среды, имеющим различно направленный вектор градиента скорости [2].

В данной работе представлены результаты исследований взаимозависимых тенденций ритмической активности, которые, возможно, отражаютантагонизм противодействия факторов регулирующих Солнечную активность.

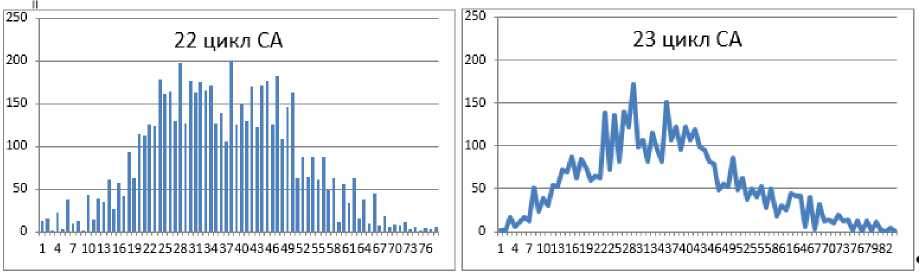
Рис. 1. Динамика Солнечной активности по числу солнечных пятен

Методы исследования.Разложение динамической вариабельности на показатели доле- вых тенденций (ДТ) приведены в схеме.

Схема последовательных вычислений:

∆± = Ci+1 – Ci. Выделение амплитуд(1)

Bi = (pi + pi+1) + n /ArccosZa.   Доля прироста(2)

By= Bi — hst .     Выбор стандарта(3)

ДУУij = Ву + Ву+1.   Доля условного участия(4)

ДУАij = ДУУij / n – 1 Доля условной активности(5)

КЕ = ДУУ * ДУА. Кумулятивная емкость(6)

РДС = 1/ [√ Σ(ДУУ i – ДУУ j )²/n – 1]. Резерв динамического сопряжения (7)

Вх = √ (Вji – ОРинт)2. Выбор тенденции гармоник(8)

НВх= Вх + Вх+1. Накопительная вариабельность(9)

КЕ-2 = ДУУх * ДУАх.   Кумулятивная емкость - 2(10)

ДСА=[(НВ i + НВ j )/НВ j ]–[(НВ i + НВ j )/НВ i ].

Диапазон системных антагонистов (ДСА)(11)

Р = limm/n. Вероятность исхода (12)

На первом этапе, в динамике СА между предыдущим и последующим показателями определяется величина амплитуды активности (формула-1), ряд которых представляет гармонику. Свойства гармоники, как показывают исследования [10], допол- няют статистику накопительной вариабельности (НВ). Из рисунка (рис. 2) мы видим, что гармоника (ОР) вариабельна по отношению к тенденции СА (НАТ), но, в 22 и 23 циклах ее динамика различается.

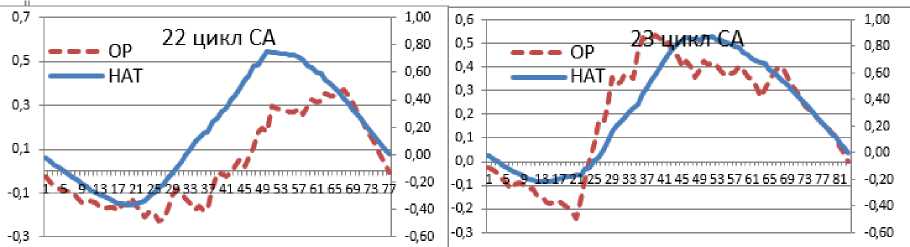
Рис. 2. Форма дуг (пассивная и активная) возрастающей и убывающей солнечной активности в динамике временного ряда (НАТ) и ее гармоника (ОР)

Различаются так же и показатели натуральных величин СА (НАТ), выраженные в показателях Долевой Тенденции (ДТ), которые состоят из двух дуг. Первая, прогнутая дуга характеризует тенденции НВ восходящей ветви, а выпуклая дуга - тенденции НВ нисходящей ветви [3].

Тенденция доли в форме дуг характеризует свойства НВ. Накопительные тенденции в системе скользящих координат (формула-2) определяют двухкомпонентную зависимость, которая состоит из тен- денции формы и тенденции итогового накопления. Графики дуг (рис. 2) отражают особенности итогового накопления, которое может быть или возрастающим, или убывающим, а сам процесс накопления может идти или активно или пассивно (рис. 3).

В дальнейшем удаление ДТ стандарта (формула-3) дает горизонтальное размещение ряда СА в Декартовой системе координат (рис. 2).

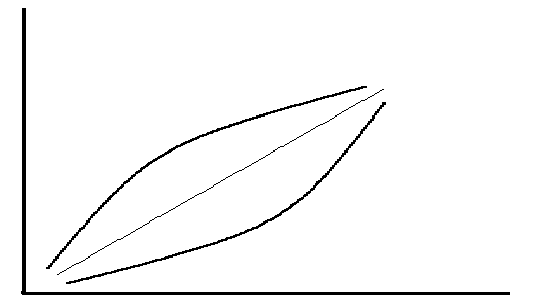
Рис. 3. Формы накопительной тенденции

Выпуклая дуга – активная, прогнутая дуга – пассивная.

На следующем этапе последовательные амплитуды в динамическом ряде гармоники, имеющие знак (+), выбираются и формируются в отдельный динамический ряд. В системной регуляции этот ряд будет характеризовать влияние факторов, способ- ствующих повышению СА. А, выделенные амплитудные значения, имеющие знак (-), будут характеризовать факторные влияния, которые уменьшают СА. Следует отметить, что как в восходящей, так и в нисходящей ветви СА (рис. 1), наблюдается поочередное то увеличение, то снижение показателя числа СА.

Двухкомпонентную зависимость тенденции формы и тенденции итогового накопления в возрастающей ветви 11 летнего цикла будет характеризовать пассив-но-возрастающую тенденцию (рис. 2), а в убывающей ветви будет представлять формы активно-убывающей тенденции.

В результате разделения ряда СА на дополнительные ряды мы получаем ряды уровневой иерархии, где натуральный ряд СА представляет 1-й уровень иерархии, гармоника - 2-й уровень, а выделенные из гармоники ряды, состоящие из (+) и (-) амплитуд, ряды 3-го уровня. Дальнейшее разделение гармоники рядов 3-го уровня дает дополнительные ряды 4-6 уровней.

Данный подход в разделении целого и изучении свойств его частей в методологии элементаризма и холизма позволяет выделить возникновение форм противоречий, которые составляют взаимозависимость и взаимоотрицание противоположностей [7].

Зависимость тенденции формы и тенденции итогового накопления [10] определяется по представленной таблице 1. Убывающее (возрастающее) накопление может иметь две формы активности: или активную, или пассивную. Например, если накопительная вариабельность показателей в восходящей ветви 11 летнего цикла СА [3] находится в отрицательной зоне (то есть ниже изолинии), то такая зависимость будет пассивно-возрастающей (Рис.2, прогнутая дуга, НАТ). Если накопительная вариабельность в нисходящей ветви показателей СА будет находится выше изолинии, то такая зависимость будет активно-убывающей (рис. 2, выпуклая форма дуги, НАТ).

Таблица 1. Определение форм антагонистических взаимодействий

Накопительная вариабельность	Тенденция формы		Итог накопления
	активная	пассивная	возрастающий	убывающий
Активно-возрастающая	+		+
Пассивно-возрастающая		-	+
Активно-убывающая	+			-
Пассивно-убывающая		-		-

Результаты исследований и их обсуждение. Как мы видим из графика (рис. 2) гармоника по отношению к общему ряду имеет достаточно самостоятельную тенденцию, что говорит о неизвестных нам факторах влияющих на изменение СА.

Используя холистический подход, нами из гармоники были выбраны в отдельные ряды показатели, имеющие положительный и отрицательный знак. Долевая тенденция (ДТ) этих рядов представлена на рисунке 4.

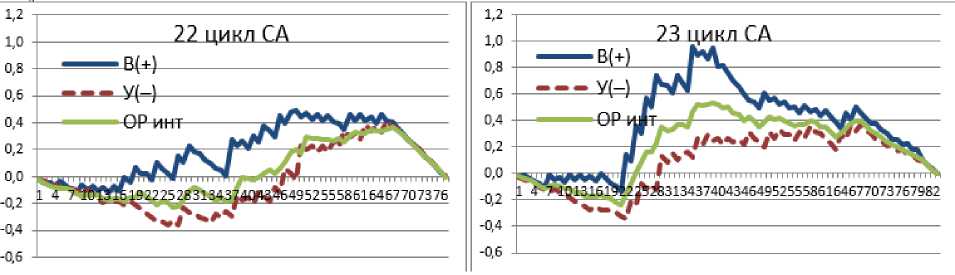
Рис. 4. Вариабельность амплитудных рядов (В (+) возрастающего и У (-) убывающего) выбранных из гармоники (ОР инт , 2-й уровень иерархии)

Тенденция ряда положительных и отрицательных амплитуд в целом характери- зуют процесс возрастающей (В(+)) и убывающей (У(-)) СА (рис. 4). Графики 22 и

23 циклов показывают большие различия между ними в тенденциях и формах, которые мы приводим к единым расчетным показателям (табл. 2). Из таблицы мы видим, что показатели кумулятивной емкости (КЕ, 3,21) 23 цикла выше показателей

22 цикла. Показатели В(+) и У(–), как мы видим (рис. 4), содержат тенденции гармоники для которой характерна, так же как и для временного ряда, пассивно-возрастающая и активно-убывающая тенденции (рис. 2).

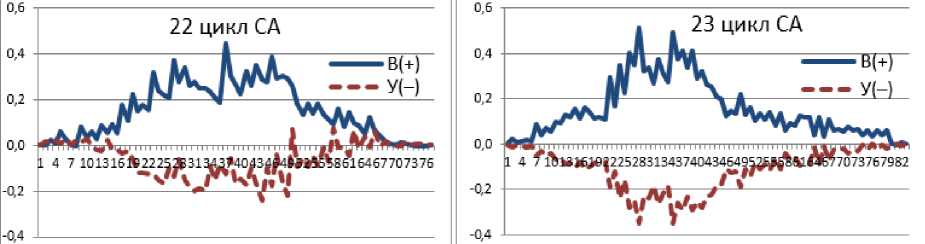
Рис. 5. Из динамических рядов 3-го уровня удалена тенденция гармоники

Удаление этой тенденции (В ji – ОР инт ) позволяет получить динамическую взаимозависимость между возрастающей и убывающей тенденциями СА (рис. 5). Из графиков видно, что в 22 цикле величина активно-возрастающей тенденции (формула-9) значительно выше тенденции пас-сивно-убывающей (табл. 2, Р нв+ 0,68, Р нв—

0,32 ), в 23 цикле различия в диапазонах тенденций значительно ниже (Табл.2, Р НВ+ 0,58, Р нв— 0,42 ).

Кумулятивная емкость (КЕ-2, табл. 2;1,77;-0,25) также подчеркивает большую нестабильность между динамическими процессами в 22 цикле (рис. 6).

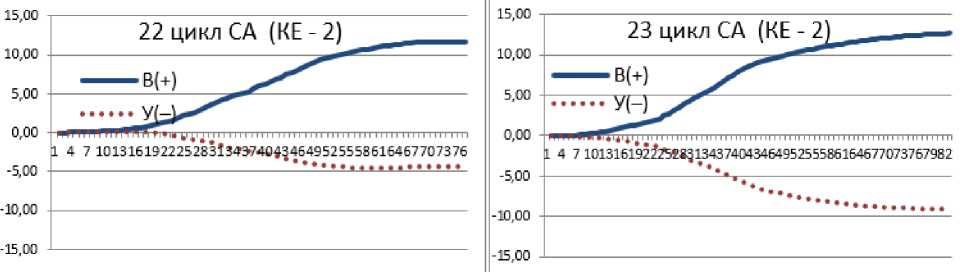
Рис. 6. Накопление (КЕ-2) активно- возрастающих (В (+) ) и пассивно-убывающих (У (-) ) тенденций в динамических рядах 3-го уровня иерархии

Нахождение возрастающих амплитуд (Рис.6,В(+)) в положительной зоне системных координат говорит об активно-возрастающих тенденциях, а нахождение убывающих амплитуд У(-) в отрицатель- ной зоне о пассивно-убывающих тенденциях (табл. 1). Преобладание в антагонизме доли активно-возрастающих тенденций (В(+)) указывает на их доминирующую роль в повышении СА [2, 4, 6].

Таблица 2. Антагонизм в динамике первичных признаков (1-3 уровень)

ТЕНДЕНЦИИ	долевые показатели	22 цикл	23 цикл
Тенд-ция СА	КЕ	2,04	8,04
гармоника	КЕ	0,08	3,21
Возраст.(+)	КЕ-2	1,77	1,95
Убывающ.(-)	КЕ-2	-0,25	-1,00
Возраст.(+)	нв+	1,47	1,72
Убывающ.(-)	нв-	3,11	2,40
Возраст.(+)	Р нв+	0,68	0,58
Убывающ.(-)	Р нв–	0,32	0,42
(в + ) + (У - )	Енв	17,2	21,7
(у - ) -(в + )	ДСА	1,63	0,68

Показатель КЕ-2 В 22 (1,77 и -0,25) и 23 (1,95 и -1,00) циклах характеризует антагонизм между активно-возрастающей и пассивно-убывающей тенденциями (Табл.1). Диапазон между этими формами в 22 цикле (1,63) значительно превосходит показатель 23 цикл (Рнв+0,68), что, соответственно, указывает на преобладающее влияние активно-возрастающей тенденции в 22 цикле (Рис.5 и 6). В антагонизме 23 цикла мы наблюдаем большее равновесие сил, которое, однако, сопровождается большим диапазоном амплитудных вариаций (2нв21,7,КЕ-21,95 и -1,00).

Дальнейшее разделение амплитудных рядов 3-го уровня иерархии (рис. 4 В (+) и У (-) ), имеющих тенденции гармоники, на дополнительные ряды 4-го - 6-го уровней позволило получить вторичные признаки возрастающих и убывающих тенденций (рис. 7 и 8).

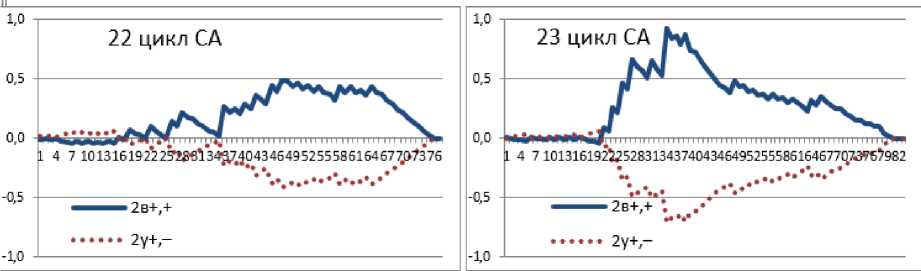
Рис. 7. Вторичные признаки возрастающих 2в+,+ и убывающих 2у+,- тенденций в дина- мике 3-го уровня иерархии (рис. 4 В(+))

После выделения дополнительных амплитудных рядов все последующие вычисления показателей долевых тенденций вновь повторяются (формулы 2-12). Полученные формы вторичных признаков позволили выявить признак взаимозаменяемости тенденции формы и тенденции итогового накопления (Рис.7 и 8). Так, например, первоначальная дуга пассивно-возрастающей тенденции (Рис.7 2в+,+), в дальнейшем заменилась активно-возрастающей формой, а противоположная ей активно-убывающая тенденция, наоборот, приобрела пассивную форму (рис. 7 2у+,-).

Более выраженные характеристики взаимозаменяемости вторичных признаков мы наблюдаем в антагонизме активно-убывающей 2у(-,-) и пассивно-возрастающей 2в(–,+) тенденции, которые во второй половине переходят в другие зоны графика изменяя форму на активно-возрастающую 2в(–,+) и пассивно– убывающую тенденции 2у(-,-) (рис. 8).

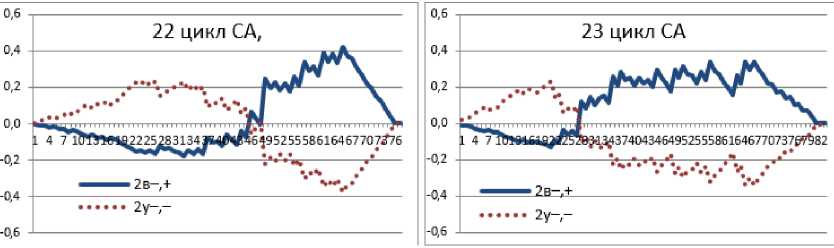
Рис. 8. Вторичные признаки возрастающих 2в(–,+) и убывающих 2у(–,–) тенденций в динамике 3-го уровня иерархии (рис. 4 У (–) )

Таким образом, антагонизм между возрастающими и убывающими тенденциями вторичных признаков имеет взаимозаменяемые активные и пассивные формы, которые различны во временных интервалах как для 22, так и для 23 одиннадцати летного цикла СА (рис. 8).

Сама принцип итогового накопления, как явление, достаточно широко распро- странено в природе [5], но, для того, чтобы выделить его в динамике временного ряда, необходимо измерение накопительной вариабельности в показателях долевой тенденции (табл. 3), которая в итоге и определяет форму взаимозаменяемости дуг (рис. 2 и 3).

Таблица 3. Антагонизм в динамике вторичных признаков (4-6 уровень)

Тенденции 22 цикла СА				Тенденции 23 цикла СА
возрастающие(+)		Убывающие (–)		возрастающие(+)		Убывающие (–)
КЕ 2(+,+) КЕ 2(+,-)	2,63 –2,01	КЕ 2(-,+) КЕ 2(-,-)	0,09 –0,01	КЕ 2(+,+) КЕ 2(+,-)	6,86 –5,40	КЕ 2(-,+) КЕ 2(-,-)	1,06 –0,73
НВ (+,+)	1,90	НВ (-,+)	2,07	НВ (+,+)	1,90	НВ (-,+)	2,09
НВ (+,-)	2,11	нв (-,-)	1,93	НВ (+,-)	2,11	нв (-,-)	1,92
Р нв+,+	0,53	Р нв,-	0,48	Р нв+,+	0,53	Р нв-,+	0,48
Р нв+,-	0,47	Р нв-,-	0,52	Р нв+,-	0,47	Р нв-,-	0,52
ЕНВ	28,5	ЕНВ	23,4	ЕНВ	45,9	ЕНВ	27,3
ДСА	0,21	ДСА	0,14	ДСА	0,21	ДСА	0,17

Из таблицы мы видим, что между вторичными признаками, как показывает диапазон системных антагонистов (ДСА), в возрастающих тенденциях (табл. 3, ДСА; 0,21 и 0,21) антагонизм между факторами более активен, чем в тенденциях убывающих (ДСА; 0,14 и 0,17).

Величина накопительной вариабельности (НВ) вторичных признаков представляет своеобразные весы равновесия в антагонизме между парами воздействующих признаков (2в+,+ и 2у+,–) и между (2в–,+ и 2у–,–).

Кумулятивный показатель (КЕ-2) в таблице указывает на преобладание в антагонизме или пассивной ( х ,–), или активной формы ( х ,+), где второй знак говорит о форме. Для 22 и для 23 цикла характерно преобладание активных форм (КЕ-2

2,63;0,09;6,86;1,06) как для возрастающих, так и для убывающих тенденций. Следует отметить большую активность возрастающих тенденций (КЕ-2 2,63 и 6,86) в динамике 22 и 23 цикла СА.

Выводы.

• 1.    В динамике временного ряда 11-ти летнего цикла СА определяется числами Вольфа. Взаимозависимость СА ветвей роста и спада в цикле может оцениваться показателями форм долевых тенденций. В результате исследований было установлено, что на 1-м уровне иерархии в 22 и 23 цикле антагонизм проявляется между тенденциями, имеющих пассивную и активную формы (рис. 2).

• 2.    Выделение из временного ряда СА возрастающих и убывающих амплитуд дает нам показатель вариации ритма актив-

• ности (2-й уровень иерархии). Долевые тенденции в отобранных амплитудных рядах представляют 3-й уровень иерархии. Антагонизм в этих рядах проявляется ак-тивно-возрастающей и пассивно-убывающей тенденциями (рис. 5).

• 3.    Дальнейшее разделение амплитудных вариаций возрастающей и убывающей

• 4.    Признак взаимозаменяемости отражает состояние временного доминирова-

• ния между активным и пассивным накоп лением, между возрастающим и убываю щим накоплением.

тенденции дает антагонизм в динамике вторичных признаков. В парах возрастающей и убывающей активности проявляется антагонизм противодействия между внешними и внутренними факторами Солнечной системы, которые влияют на вариабельность ритма Солнечной активности. Было установлено, что в возрастающих тенденциях антагонизм более активен, чем в тенденциях убывающих.