Anti-Forensics of JPEG Images using Interpolation

Published Online November 2015 in MECS

Due to advancement of computation and communication technologies, there are easily available good quality photo capturing devices and photo editing softwares. These indirectly or directly help to make visually good quality doctored images that may create intentionally or unintentionally problems in personal, political and public life. The existing methods for digital image forensics are passive and blind because they are not based on any watermark or signature. Quite good amount of research work has been done in the field of image forensics [1-5]. Farid [2] reports that splicing two images of different JPEG compression quality is helpful in detection of forgery. It is mentioned in [3] that there is re-quantization in digital multimedia content when there is tampering in it. Therefore detection of re-quantization is an important element for assessing the authenticity of a digital image.

Some researchers have developed their counter forensic, also called antiforensics technique, so that forgery cannot be detected easily [6-10]. Basically these papers do antiforensics by adding noise or blurring the image so that forgery is not detectable. Antiforensic does help in finding the limitations of the forensic techniques that in turn forces to develop more robust forensic techniques. The forensic and antiforensics techniques may be considered analogous to virus and antivirus.

The digital images are stored in various formats such as .tiff, .pcx, .png, .bmp, .jpeg. The JPEG standard is one of the most popular standards because it can provide zero (lossless) compression to any good amount of compression depending upon the requirement and at the same time it maintains good quality of image. There have been several techniques to detect forgery in JPEG images [11-17]. Forgery detection in a JPEG image is indirectly helped due to its own compression artifacts. In a JPEG image, two types of artifact appear: quantization artifacts in frequency domain and blocking artifacts in spatial domain. If image tempering is done, then the image needs to be saved two times that creates double quantization artifact in histogram of DCT coefficients and the block synchronization gets disturbed. With the help of these artifacts forgery detection can be done easily. An attacker tries to hide or reduce these artifacts so that his forgery cannot be detected. While hiding or reducing the artifacts the image quality gets compromised by these methods. In this paper we discuss interpolation techniques that hide or reduce the artifacts and at the same time maintain image quality. We compare the quality of the interpolated images with some available state of the art quality assessment measures that include mean square error (MSE), peak signal to noise ratio (PSNR), structural similarity index (SSIM) [18] and blind image spatial quality evaluator (BRISQUE) [19].

Rest of the paper is organized as follows. Section 2 reviews the related work and section 3 discusses the interpolation methods. The experimental results are given in section 4 and the paper is concluded in section 5.

• II.    Related Work

Latest developments help provide multimedia data in digital form, which can easily be spliced and cloned. It may sometime encourage digital piracy that may lead to financial losses to the owner. Sometimes a person having bad intention may misuse this capability of digital media to forge an image. This has been done in past in several cases. For example, in order to taking political benefit, Kenyan politician Mike Sonko posted an image (Figure 1) on Facebook of himself being embraced by the Mandela.

However someone ultimately found the original photo, in which Mandela was actually embracing boxer Muhammad Ali against a completely different background.

1 (a)                                 1 (b)

Fig.1. (a) Fake image in which Mandela embracing Mike Sonko (b) Original image in which Mandela embracing Muhammad Ali

In Denmark in the year 2013 the social media showed an of powerful storm image (Figure 2) to create sensational news that was ultimately found to be spliced. It was discovered that the storm cloud featured in the image closely matched with the storm of Montana in 2010.

Fig.2. Doctored Image of Storm in Denmark

Depending on the operation the image forgery may be categorized into two broad groups: image splicing and copy-move forgery. In splicing forgery, two or more different images are used to create fake image and in copy-move forgery the replication of a portion of the same image is used to create fake image. To counteract the problem of forgery, several methods have been developed for forgery detection in digital images. The paper [20] discusses that the image forgery (copy-move) can be identified in DCT domain. In this method DCT coefficients are calculated of image overlapping blocks and signs of these DCT coefficients is used as a feature. Farid [21] reports that image forgeries can be identified by calculating the lighting angle of different objects and their synchronization. Lukas et al [22] discuss that the falsified regions in an image can be detected by knowing the photo response non uniformity (PRNU) noise of the camera. If in an image various values of PRNU noise exist then image may be forged. The paper [23] discusses that only one light sensor can be used in camera instead of the three sensors due to the cost factor. Since we need three different colors (RGB), the color filter array (CFA) is used to create these colors from the data obtained by using single sensor. The different cameras have different CFA patterns and different interpolation methods. So by finding the CFA pattern and the interpolation methods, the authenticity of an image can be decided.

One of the important formats for storing digital images is JPEG standard because it perhaps provides good quality using less storage. Accordingly there have been several methods for detecting forgery in JPEG images [11-17]. JPEG image forgery detection can be based on the quantization artifacts or/and blocking artifacts. The Forensic techniques based on the quantization artifacts [11-13] identify image forgery by detecting localized inconsistencies in DCT domain. The localized inconsistency occurs only when if one of the two images used to create forgery was previously JPEG compressed image. There occur periodic/regular patterns in DCT coefficients of the corresponding regions in the image that was previously compressed. The forensic methods [14-17] find the irregularities in spatial domain based on the blocking artifacts. If the grid boundaries of the pasted regions do not synchronize with that of the background image, then the pasted regions will have different grid boundaries with respect to that background image.

Generally the tampered images have to be restored two times that creates double quantization artifacts in the histogram of the DCT coefficients and the blocking pattern, which is generally of 8x8 pixels, in the spatial domain also gets distorted. An attacker with the help of this information can make changes in the image so that traces of the forgery become non-detectable. Removing the traces of both types of artifacts is generally referred as antiforensics. Antiforensic techniques prevent proper forensic investigation process or make it much harder. These techniques reduce quantity and quality of the evidences present in a digital image thus making the analysis and examination of the evidences difficult or impossible.

For concealing the JPEG compression traces in digital images many antiforensic techniques are available. One of the most popular techniques proposed by Stamm et al. [6] is based on dithering. Dithering removes the quantization artifacts in DCT coefficients by filling the gaps. The blocking artifacts are removed by adding some signals in the image. However, the paper [7] reports that the operations performed in [6] introduce noise in the image and decrease the visual quality of the image. The singly compressed JPEG images follow the Benford’s law that states, “the probability distribution of first digits of the DCT block coefficients is logarithmic.” However the doubly compressed images do not follow this distribution [24]. Some antiforensic techniques have been discussed based on the Benford’s law. In order to make a doubly compressed image non-detectable, Milani et al. [8] modify the statistics of the first digits of the DCT block coefficients by redistributing of data in which the difference of the actual DCT coefficients and the estimated coefficients using the Benford’s law is minimized. The paper [9] discusses an anti-forensic method that conceals the traces of singly JPEG compressed image by recovering the distribution of first significant digits of the original DCT coefficients by operating on the distribution of their logarithmic remainders. However the above mentioned methods [8-9] are complex and also create distortion in the image. In [10], it is reported that the DCT coefficients do not follow Laplacian distribution for all type of images as discussed in [6]. In that paper a non-parametric method based on DCT histogram smoothing without using any statistical model is discussed. However, Fan et al [25] report that the method [10] is not suitable for the images which have large smooth regions. In that method, the DCT coefficients are calculated using the total variationbased deblocking operation. These DCT coefficients create an adaptive local dithering signal model that brings the DCT histogram of the processed image close to that of the original one. The paper [26] tries to remove the traces of JPEG compression by adding the tailored noise that converts the DCT coefficients of the compressed image such that their distribution is similar to that of the uncompressed image. However, this noise sacrifices the image visual quality. In this paper, we discuss application of interpolation techniques as image anti-forensics that can conceal the footprints of JPEG compression and also maintain good visual quality of the images.

• III.    Interpolation Methods

In this section we discuss a process to remove JPEG artifacts in images. In JPEG artifacts, the histogram of some of the DCT values does not occur continuously unlike in the uncompressed DCT values. It means that some of the DCT values in JPEG artifacts are zero that needs to be found out. For finding these missing values some interpolation methods can be applied. The interpolation methods are of two types: adaptive and non-adaptive.

Adaptive interpolation is applied based on the characteristics of image (sharp edges vs. smooth texture) to compute missing values. Non-adaptive interpolation uses the predetermined pattern of computation to recover the missing values irrespective of the image characteristics. The adaptive interpolation methods are difficult to implement and require more computation time; thus they are less preferred. On the other hand, the non-adaptive interpolation methods are simple to implement and require less computation. The most commonly used non-adaptive interpolation methods are nearest neighbor [27], bilinear [27] and bicubic interpolation methods [28], depending on the number of neighboring pixels used to calculate the missing pixel value.

• A.    Nearest Neighbor Interpolation

This is the simplest interpolation method and requires least processing time. It considers only one pixel to estimate the missing pixel value. Each interpolated output pixel is assigned the value of the nearest sample point in the input image.

• B.    Bilinear Interpolation

In bilinear interpolation, the adjoining 2×2 neighborhood of known pixel values surrounding the unknown pixel are considered. The value of the unknown pixel is obtained by taking the weighted average of these four pixels. Let I(x, y) denote the intensity of the unknown pixel at position (x, y) andI(x , y ) , I(x , y ) , I(x , y ) andI(x , y )be the intensities of its 2×2 four neighbors positioned at (x, y) , (x, y) , (x, y) and (x, y) . The value of I at the interpolated point in the image can be estimated as

I ( x , y ) = W j I ( X j , y j ) + w 2 1 ( x 2 , У 1 ) + W 3 1 ( X j , y 2 ) + W 4 1 ( X 2 , y 2 )

Where wi , i = 1 to 4 are the weights that are decided according to the distance, close pixels assigned higher weights as compared to the far pixels [27]. Since it considers the average value of four neighbor pixels, it provides much smoother looking images as compared to the nearest neighbor interpolation in which the missing pixel value is replaced by a single pixel.

• C.    Bicubic Interpolation

The bicubic interpolation considers a neighbor of 4×4 pixels for estimating the missing pixel value. The general form for a Bicubic interpolation is as follows:

I (x, y )=EE Vy = i=0 j=0

a ₀₀ + a₁₀x + a₀₁y + a_uxy + a_my + a₂₁x y +

222333 a _j2 xy + a ₂₂ xy + a ₃₀ x + a ₀₃ y + a _3j xy +

3     32     23    33

a₁₃xy + a₃₂x y + a₂₃x y + a₃₃x y

The coefficients aij , i,j=0,1,2,3 are obtained by calculating the gradients in both x and y directions and the cross derivative at each of the four corners of square. The bicubic interpolation produces sharper images than the nearest neighbor and bilinear interpolation methods both and it is perhaps the ideal combination of processing time and output quality. For this reason it is a standard in most of the image editing softwares and image capturing devices.

We will apply the above mentioned interpolation techniques to JPEG images in order to remove their artifacts. Basically these artifacts are due to some missing values in the DCT histogram, which are filled using interpolation. Once these missing values are obtained, the image forgery detection methods based on JPEG artifacts cannot identify the JPEG compression history of the image.

• IV.    Experimental Results

3(a5)                      3(b5)                     3(c5)                    3(d5)

We have used various quality parameters namely mean square error (MSE), peak signal to noise ratio (PSNR), structural similarity index (SSIM)[18] and blind image spatial quality evaluator (BRISQUE)[19].

• A.    Mean Square Error (MSE)

It is defined as the average squared difference between the reference image (P) and the distorted image (Q), each of size m×n. It is calculated pixel-by-pixel by adding up the squared differences of all the pixels and dividing by the total number of pixels. It is computed by the following formula- m-1 n-1

MSE -= Ш p ( i . j ) - Q ( i . j ) ]       (3)

^mn i - 0 j - 0

• B.    Peak Signal to Noise Ratio (PSNR)

It is defined as follows-

PSNR - 10.log₁₀ [ L/MSE ]             (4)

Where L is the dynamic range of the pixel values.

Higher PSNR value indicates higher quality of the image.

• C.    Structural Similarity Index (SSIM) [18]

MSE and PSNR are computationally simple but they don’t consider viewing conditions and the characteristics of the human visual perception. The SSIM is based on the local luminance, contrast and structural information. It is computed as follows-

(2 д и + C)(2 a + D )

SSIM -    ,  x?----' , xy , '

(U_x ² + U 2 + C )(^_x ² + ст, ² + D )

Where и. и are the mean intensity. ^. ^, are the standard deviation. ст is the covariance and C. D are the xy constants.

• D.    Blind Image Spatial Quality Evaluator (BRISQUE) [19]

This image quality assessment model is based on natural scene statistics. This model is highly correlates with human subjective scores. It computes Mean subtracted contrast normalized coefficients (MSCN) over the whole image. For an image I, the MSCN coefficient image, Î, is computed by j = I (i, j) - ^( i, j)               (6)

a ( i , j ) + C

In case of PSNR also the bicubic interpolated images have the best performance as evident from Table 2. The performance of bicubic interpolated image is followed by bilinear interpolated images and finally nearest neighbor interpolated images.

KL where Кi, j) = E E Wk,ilk,i (i, j) and k =- Kl=-L

KL

^ (i , j ) =JE E w k , i ⁽ I k , i ⁽ i , j ) - ^ ⁽ i , j ⁾⁾² V k =- Kl =- L

Here w = { w_k, J k = - K ,, K , l = - L ,, L } is a 2D circularly-symmetric weighting function and C is a constant.

With the help of MSCN, image quality is evaluated in SSIM.

The MSE, PSNR and SSIM are full-reference quality assessment measures; they require the original undistorted image to compare with the distorted image. The BRISQUE is no-reference quality assessment measure; it does not require any reference image for quality assessment.

We have compute the above mentioned performance parameters MSE, PSNR, SSIM and BRISQUE and their values are given in Tables 1, 2, 3 and 4 respectively. The smaller value of MSE and BRISQUE parameters indicate the good quality of the image, where as higher values of PSNR and SSIM indicate the good quality of the image.

We observe from Table 1 that the MSE value is best for bicubic interpolated images taken in our experiments for all images, followed by bilinear interpolated images and finally nearest neighbor interpolated images.

Table 2. PSNR of Images using Different Interpolation Methods

Test Images	Peak signal to noise ratio for the test images taken from USC SIPI database [29]
	Bicubic	Bilinear	Nearest
Stream & bridge	28.413	27.484	24.291
Tank 1	35.781	34.766	31.325
Car & APCs 1	37.494	36.451	32.991
Fishing Boat	32.596	31.525	28.252
Girl (Elaine)	32.756	31.741	28.297
Couple	33.746	32.736	29.331
Aerial	38.212	36.891	33.581
Truck	34.296	33.004	29.761
Airplane	38.264	37.048	33.348
Tank 2	31.607	30.788	27.162
Car & APCs 2	35.583	34.832	31.142
Truck & APCs 1	30.253	29.285	26.831
Truck & APCs 2	28.709	27.851	24.272
Tank 3	36.137	35.081	31.576
APC	37.338	36.607	32.98147

Same is the case for SSIM parameter as shown in Table 3.

Table 1. MSE for Different Images using Different Interpolation Methods

Test Images	Mean Square Error for the test images taken from USC SIPI database [29]
	Bicubic	Bilinear	Nearest
Stream & bridge	93.709	116.056	242.102
Tank 1	17.182	21.699	47.924
Car & APCs 1	11.576	14.721	32.663
Fishing Boat	35.763	45.761	97.247
Girl (Elaine)	34.472	43.541	96.244
Couple	27.446	34.624	75.856
Aerial	9.813	13.301	28.503
Truck	24.179	32.556	68.692
Airplane	9.697	12.831	30.076
Tank 2	44.909	54.234	124.974
Car & APCs 2	17.976	21.369	49.988
Truck & APCs 1	61.344	76.645	134.861
Truck & APCs 2	87.525	106.643	243.119
Tank 3	15.824	20.179	45.234
APC	12.001	14.202	32.729

Table 3. SSIM of Images using Different Interpolation Methods

Test Images	Structural Similarity Index ratio for the test images taken from USC SIPI database [27]
	Bicubic	Bilinear	Nearest
Stream & bridge	0.8927	0.8517	0.7706
Tank 1	0.9333	0.9075	0.8462
Car & APCs 1	0.9547	0.9375	0.8828
Fishing Boat	0.9158	0.8823	0.8097
Girl (Elaine)	0.9157	0.8832	0.8055
Couple	0.9176	0.8855	0.8099
Aerial	0.9516	0.9321	0.8869
Truck	0.9239	0.8916	0.8224
Airplane	0.9567	0.9389	0.8849
Tank 2	0.9321	0.9118	0.8513
Car & APCs 2	0.9279	0.9062	0.8492
Truck & APCs 1	0.9415	0.9223	0.8659
Truck & APCs 2	0.9321	0.9046	0.8315
Tank 3	0.9442	0.9249	0.8656
APC	0.9757	0.9689	0.9469

As per the BRISQUE parameter is concern the bicubic interpolated images either have better or comparative performance in case of most of the images as shown in Table 4.

Table 4. BRISQUE of Images using Different Interpolation Methods

Test Images	Blind image spatial quality evaluator for the test images taken from USC SIPI database
	Original	Bicubic	Bilinear	Nearest
1	13.482	15.442	23.547	23.806
2	17.223	22.888	31.297	25.701
3	29.285	33.087	40.371	35.179
4	13.295	20.768	29.557	22.544
5	16.415	23.147	31.668	24.861
6	13.408	21.258	29.375	23.271
7	22.859	25.259	30.765	27.264
8	18.037	26.456	34.894	26.662
9	26.893	31.641	39.799	31.558
10	18.609	23.414	29.181	24.098
11	15.639	5.0905	13.270	20.228
12	24.781	29.096	33.522	29.012
13	17.823	24.212	28.796	27.102
14	26.888	31.348	37.826	31.337
15	33.459	31.054	35.711	35.2661

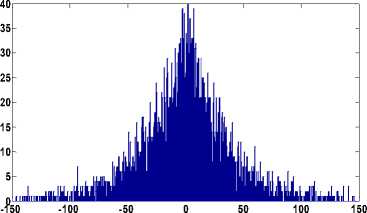
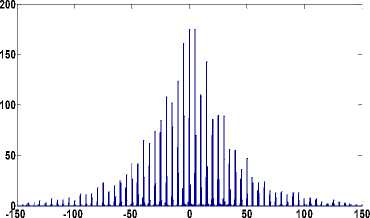
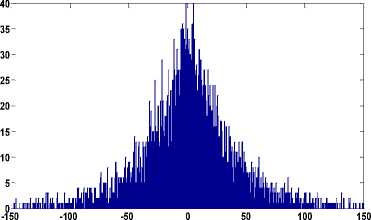
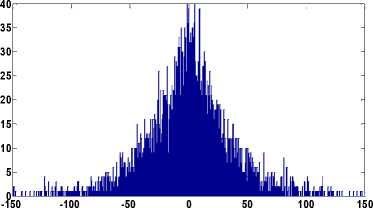
As evident from Figs. 4(d)-4(f) the histograms follow the Laplacian distribution similar to that of the uncompressed image.

4 (a)

4 (b)

4 (c)

4 (d)

4 (e)

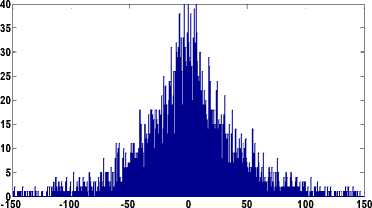
4 (f)

Fig.4. (a) Original Stream and Bridge Image (b) Histogram of (1,1) DCT Subband for (a) Image. (c) Histogram of (1,1) DCT Subband of

JPEG Compressed Image (d) Histogram of (1,1) DCT Subband of Bicubic Interpolated Image (e) Histogram of (1,1) DCT Subband of bilinear interpolated image (f) Histogram of (1,1) DCT Subband of Nearest Neighbor Interpolated Image.

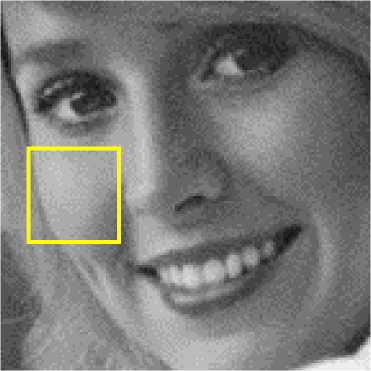
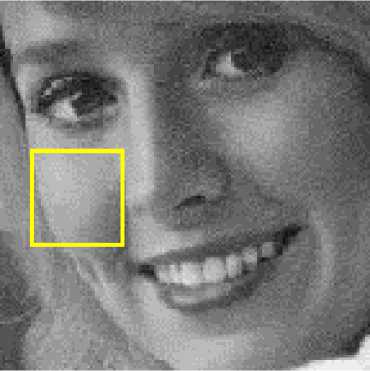
One of the artifacts of JPEG compressed images is blocking artifact as shown in Figure 5(a) inside the red rectangle. Figures 5(b)-5(d) show the bicubic, bilinear and nearest neighbor interpolated images respectively. As evident from these figures the blocking artifacts either have been removed or have been reduced significantly. Bicubic interpolated image (Fig. 5(b)) also looks best in comparison to bilinear and nearest neighbor interpolated images.

5 (a)

5 (b)

5 (c)

5 (d)

Fig.5. (a) A portion of Girl (Elaine) JPEG Compressed Image 5(b)-(d) Bicubic, Bilinear and Nearest Neighbor Interpolated Images Respectively

• V.    Conclusion And Future Work

As the JPEG compression artifacts are basis of many image forgery detection methods. So by removing these artifacts forgery detection becomes more challenging and sometimes impossible. In this paper we apply different interpolation methods and verify experimentally that JPEG compression artifacts are removed by using interpolation methods successfully. We have also verified the quality of the various antiforensic images with different state of the art quality assessment methods. We found that bicubic interpolation gives the best result for all quality assessment methods followed by bilinear interpolation and nearest neighbor interpolation methods.

This method successfully removes JPEG artifacts but it leaves traces of interpolation. To remove traces of interpolation, random selection of interpolation method can be used for each pixel. Also many other state of the art interpolation methods can be used with random selection to remove the traces of interpolation and can get the image of better quality.