Антиотражающее покрытие с металлическими наночастицами

Развитие нанотехнологии привело к взрывоподобному росту интереса исследователей (как теоретиков, так и экспериментаторов) к проблеме разработки более совершенных функциональных покрытий и структур, предназначенных для управления электромагнитными волнами. Предметом исследований стали структуры, позволяющие скрывать объекты от электромагнитного излучения [1, 2], фильтры [3], просветляющие покрытия [4], “суперлинзы” [5], электромагнитные “черные дыры” [6]. В солнечной энергетике, а также в других отраслях техники востребованы светопоглощающие (антиотражающие) покрытия, применяемые, например, для устранения паразитного переотражения и повышения эффективности фототермального преобразования. Получены высокоэффективные светопоглощающие покрытия на основе углеродных нанотрубок [7], на-ноструктурированных металлических пленок [8]. В настоящей работе исследована возможность изготовления антиотражающего (светопоглощающего) покрытия на основе гетерогенного композитного материала с металлическими наночастицами. Наличие диссипативной подсистемы -металлических частиц с плазмонным резонансом в видимой области спектра - позволяет контролировать спектральные свойства и эффективность поглощения света за счет варьирования концент-

рации и формы наночастиц. Рассмотрен случай нанокомпозита с одинаково ориентированными наночастицами в форме сплюснутых сфероидов одинакового размера.

ОСНОВНЫЕ УРАВНЕНИЯ

Одинаково ориентированные включения задают выделенное направление в композите - ось текстуры. В силу симметрии подобный композит обладает свойством двулучепреломляющего материала с оптической осью, совпадающей с ось текстуры. Свойства подобного нанокомпозита характеризуется тензором эффективной диэлектрической проницаемости следующего вида:

(£ 0 o

£ = 0 £

o

(0 0

0 ) 0

£e У

где главные значения представлены величинами £ e и £ o , отвечающими продольной и поперечной поляризации света относительно оси текстуры композита, то есть необыкновенному и обыкновенному лучам. В рамках модели эффективной среды Максвелла-Гарнета для композита с изотропной матрицей можно записать [9,10]:

£m +(g£r £m )П 1 +(g£m - 1)^ ’

£m +( g l£p I" £m )П 1 + (g£ - 1)П

где £ m и £ p — диэлектрические проницаемости матрицы и включений, П — объемная доля включений,

g || =

£

m

£ + L„ (£ - £ ) , m||p|| m

g. =         ^£ m

£ + L. ( £ . - £ ) ^.          (3)

m ± v p ± m /

Предполагается, что матрица нанокомпозита представлена непоглощающей средой с показателем преломления n _m = J£_m E ^ . В настоящей работе диэлектрическая функция металлической наночастицы рассматривается с учетом ограничения длины свободного пробега электрона из-за его столкновений с поверхностью частицы [11], поэтому диэлектрические проницаемости частиц несферической формы для продольной £ p и поперечной £ _{p ±} поляризации могут отличаться, что учтено в выражениях (3). Факторы деполяризации L для поля, направленного параллельно или перпендикулярно полярной оси сфероида, в длинноволновом приближении рассчитываются по формулам

1 7 _е arcsin 71 - ^²

■ 1 ^{1 -} ‘ ^Т" J

L i = ( 1 - L^ /2 ,            (4)

цах среда – пленка – подложка и изменение фазы ( P _p s ), претерпеваемой волной при прохождении через пленку, для p - и s -поляризации имеют следующий вид [12]:

r p

t p

t s

r 1 p ⁺ r 2 p ^eX P ^(- i2Pp )

1 + r1 pr2p exP(- i2Pp ) ’ r1 s + r2s exP(- iЖ )

1 + r1 sr2s exP(- iЖ ) ’ t 1 pt2p exP(- iPp )

1 + r1 p r2p exP(- i2Pp ) ’ t 1 st2s exP(- iPs )

^{1 +} r 1 s r 2 s exP ^{( -} i Ж ⁾ ’

где изменение фазы, отличающееся для p - и s -поляризации, определяется выражениями

P = 2 л— no-Jn ² - n ? sin² ^

Pp       Afi1        1 ’ где о есть отношение длин полярной a и экваториальной b полуосей сфероида: случай ! < 1 соответствует сплюснутому сфероиду (диску), ! > 1 - вытянутому, ! = 1 - шару. Заметим, что компоненты (2) тензора эффективной диэлектрической проницаемости нанокомпозита зависят от аспектного отношения о частицы.

В рамках приближения эффективной среды отражательная и пропускная способности композитного слоя могут быть рассчитаны на основе уравнений оптики слоистых сред. Пусть анизотропная нанокомпозитная пленка толщиной h , характеризуемая комплексными показателями преломления обыкновенного и необыкновенного лучей f i o = Jp ^ и f i e = £Т , разделяет две по-лубесконечные однородные изотропные среды с показателями преломления n 1 и n 2 . Для определенности рассмотрим случай, когда ось текстуры нанокомпозита направлена перпендикулярно границам раздела сред. Для нормального падения света отражательная и пропускная способности такой пленки не зависят от поляризации падающей световой волны.

Если падающая волна во внешней среде с показателем преломления n 1 обладает либо p -, либо s -поляризацией, то в силу симметрии рассматриваемой структуры волны, возбужденные в одноосной пленке и в подложке будут иметь ту же самую, т.е. p - или s -поляризацию. Полные амплитудные коэффициенты отражения и пропускания анизотропного слоя, выраженные через френелевские коэффициенты отражения ( r 1 p , s , r 2 p , s ) и пропускания ( t 1 p , s , t 2 p , s ) на грани-

^P s = ^{2 л} 7 7 ^{f i} 2 ^{- n} 1 ^{2 si} n² ^ 1 ’        (7)

A а френелевские коэффициенты определяются формулами

1 p

_ no n e cos ф ₁ - n 1 ^ne - n 1 Sin Ф 1 n _o n e cos Ф 1 + n 1 yjni 2 - n 1 ² Sin² Ф 1 ’

1 s

2 p

2 s

^t 1 s

t 2 p

n o - n 1 Sin Ф 1

222 ^, n o - n 1 Sin Ф 1

n e - n 1 Sin Ф 1 - n o n e cos ф 2

222, none cosф2 + n2 ^ne - n1 Sin Ф1

n o - n 1 Sin Ф 1 222 , (9)

n o - n 1 Sin Ф 1

2 n 1 C0S ф 1 pn e - ( n_e - По ) n 1 Sin Ф 1 ni _e ( fi o f _e cos ф ₁ + n 1 a] fi 2 - n 1 ² sin² Ф 1'

2 n 1 cos ф ₁

+ 7 fi o ² - П 2 sin² Ф 1 ’      ⁽¹⁰⁾

2 fi o f e ² а)п e ² - n 2 sin ² Ф 1 222  4 2222

n o n e есд Ф ₂ + n ₂ л]п_е - n , sin Ф 1 ) ^n_e - ( n e - n o ) n , sin Ф , ’

t ₂

2у no - n sin Ф1

n2 cosф2 + Jn2 - n12 sin2 ф2 .

Угол падения ф1 и угол преломления в подложке ф2 связаны законом Снеллиуса П1 SlПф| = П2 Sinф2. Отражательная R и пропускная T способности слоя рассчитываются с помощью (5)-(11) по формулам

.    , 2 T = n 2 ^C0S Ф 2

^Rp , ^ = r pp,s I ^{, p ,} s      n 1 cos ф ₁

^tp , s 2 .    (12)

ОПТИЧЕСКИЕ СВОЙСТВА

НАНОКОМПОЗИТНОГО ПОКРЫТИЯ

Принцип действия рассматриваемого светопоглощающего покрытия заключается в следующем: падающий световой луч разделяется на передней поверхности на отраженный и преломленный; преломленный луч поглощается в толще нанокомпозитного слоя; интенсивность отраженного луча максимально ослабляется за счет согласования оптических характеристик окружающей среды и слоя. В данном случае нанокомпо-зитный слой является неинтерференционным покрытием, интенсивность отраженного луча не зависит от свойств подстилающей среды и не изменяется при увеличении толщины покрытия.

Проведем оценку необходимых параметров светопоглощающего покрытия, ограничившись для упрощения анализа случаем нормального падения света. В неинтерференционном антиотражающем покрытии световой луч испытывает однократное отражение, поэтому расчет отражательной способности может быть проведен на основе френелевской формулы

R =

n1 - n n1 + n

( n 1 - n ) + k ²

-----———, где й = n + ik (n1 + n) + k есть комплексный показатель преломления покрытия (в рассматриваемом случае он отвечает обыкновенной волне). Из нее следует, что условию полного погашения отражения R = 0 при k ^ 0 невозможно удовлетворить ни при каких действительных n и n1 . Поэтому вместо полного отсутствия отражения потребуем его существенного ослабления:

( n, — n ) + k ²

/ —;2---- ^<< 1 .

( n 1 + n ) + k⁷

Неравенство (13) удовлетворяется при n = n 1,

и

k << n1 + n .

Принимая во внимание условие (14), требование к коэффициенту экстинкции покрытия запишем в следующем виде:

k <<  n 1 . (15)

Действительно, при выполнении условий (14), (15) отражение от покрытия будет существенно ослаблено:

R = -k y <<  1 .

4 n ₁ ²

Отражательная способность тем меньше, чем меньше коэффициент экстинкции светопоглощающего покрытия.

Обратим внимание на второе важное условие: преломленный луч должен быть поглощен покрытием. Несложный расчет показывает, что пленка толщиной

h > —

3k

ослабляет интенсивность волны, прошедшей через ее толщу дважды (от границы раздела с окружающей средой до поверхности подложки и обратно), более чем в 10⁴ раз, что вполне достаточно для достижения поставленной цели. Согласно неравенству (17), для оптического диапазона толщина пленки с коэффициентом экстинкции k <  0.1 должна быть не менее одного микрометра.

Наиболее интересным с прикладной точки зрения является случай, когда световой луч падает из воздуха (показатель преломления n 1 = 1 ). Этот же случай оказывается и наиболее проблемным для реализации, так как для n 1 = 1 в оптическом диапазоне практически невозможно удовлетворить условиям (14), (15) при использовании природных материалов. Однако это затруднение преодолевается при использовании плазмонного нанокомпозитного материала [4, 13].

Исследуем условия наблюдения единичного эффективного показателя преломления. Для фиксированного n = 1 действительная и мнимая части соотношений (2) образуют систему уравнений, результат решения которой зависит от величины объемной доли включений: при относительно малых з решений может не существовать, а в других случаях системе удовлетворяют одно или два значения коэффициента экстинкции k (в целях настоящего исследования выбирается меньшее из возможных значений k ). Условия формирования единичного эффективного показателя преломления для нанокомпозита с включениями вытянутой формы представлены в виде графиков на рис. 1. В качестве включений рассмотрены частицы серебра, поскольку серебро имеет наименьший коэффициент экстинкции в оптической области спектра. Расчеты диэлектрической функции серебряных частиц выполне- ны с учетом размерной коррекции [14,15]. Табличные данные для серебра приведены в работе [16].

На рис. 1 каждой длине волны X отвечает значение у ⁽¹⁾ , при котором нанокомпозит имеет единичный показатель преломления при минимально возможном коэффициенте экстинкции k W. Минимальному k W отвечает абсолютный минимум отражательной способности. Из представленных зависимостей видно, что величина n = 1 может достигаться при коэффициенте экстинкции к ⁽¹⁾ <  0 1 , чему соответствует довольно низкое значение отражательной способности R <  0.25% . Абсолютный минимум R достигается вблизи длины волны X = 450 нм при у ~ 0.1 .

Представленные на рис. 1. зависимости позволяют определить концентрацию включений и длину волны, на которой нанокомпозит будет светопоглощающим при наименьшей отражательной способности. Например, для рассматриваемого случая ^ = 1/7 оптимальным является значение у = 0.07 , если необходимо получить антиотражающее покрытие для длин волн вблизи X = 500 нм. Если объемная доля будет отличаться от указанного значения, это приведет к увеличению отражательной способности на заданной длине волны.

Изменение объемной доли включений приводит к смещению длины волны, отвечающей минимуму отражения: уменьшение концентрации включений смещает оптимальную длину волны в область более длинных волн, и наоборот. При изменении формы частиц сдвигается частота плазмонного резонанса наночастиц и, соответственно, смещается спектральная об- ласть, в которой формируется единичный показатель преломления. Таким образом, варьируя структурные параметры нанокомпозита, можно контролировать его спектральные характеристики.

На рис. 2 представлена зависимость отражательной способности нанокомпозитного покрытия от длины волны и угла падения света. Эффект слабопоглощающего покрытия наблюдается в коротковолновой части видимой области спектра вблизи длины волны X = 500 нм. В этой области спектра эффективный показатель преломления близок к вакуумному и выполняется условие (15). С увеличением угла падения отражательная способность монотонно растет для s -поляризованно-го света. Для p -поляризации угловая зависимость имеет минимум, обусловленный эффектом Брюстера, что положительно сказывается на антиотражающих свойствах покрытия.

В силу симметрии структуры для s -поляризации в композитном слое формируется только обыкновенный луч, при этом оптические характеристики слоя обусловлены только поперечным (по отношению к полярной оси сфероидов) плазмонным резонансом. Для p -поляризации при любом угле падения, отличном от 0, в композитном слое формируются обыкновенный и необыкновенный лучи, возбуждаются как поперечный, так и продольный резонансы. Частота продольного плазмонного резонанса сильно смещена в коротковолновую область (находится вне пределов видимой области), поэтому он практически не влияет на угловую и спектральную зависимости отражательной способности.

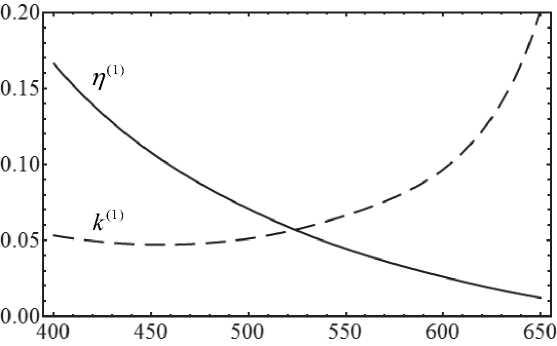
X , нм

Рис. 1. Наименьшие значения эффективного коэффициента экстинкции к ⁽¹⁾ (штриховая линия), достигаемые при объемной доле включений у ⁽¹⁾ (сплошная линия), в нанокомпозитной среде с единичным эффективным показателем преломления. Серебряные включения имеют форму сплюснутых сфероидов. Вектор электрического поля световой волны направлен перпендикулярно оси текстуры композита (случай обыкновенной волны). Параметры расчета: n m = 1.5 , § = 1/7

(а)

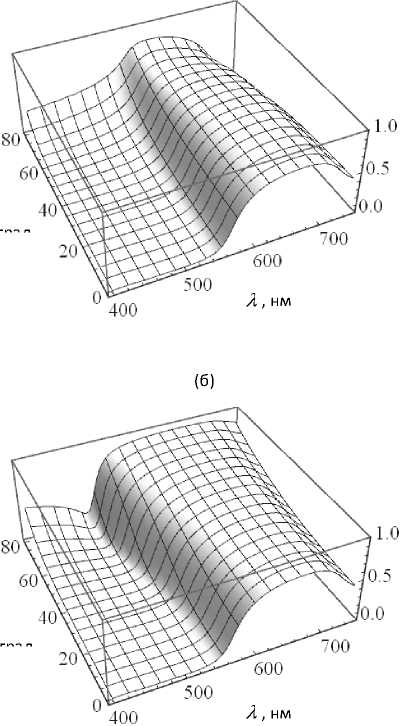
R p

R s

Рис. 2. Зависимость отражательной способности нанокомпозитного слоя от угла падения и длины световой волны для (а) p - и (б) s -поляризации света.

Значения расчетных параметров: толщина пленки h = 5 мкм, n m = 1.5 , £ = 1/7 , ^ = 0.07

Ф 1 , град.

Ф 1 , град.

В длинноволновой части спектра (в области плазмонного резонанса наночастиц) условие (14) нарушается и возникает сильное отражение падающей световой волны. Переходная область от сильного к слабому отражению смещается по частоте при изменении аспектного отношения наночастиц, что объясняется частотным смещением плазмонного резонанса. Переходная область сдвигается в коротковолновую часть спектра при приближении формы включений к сферической, и наоборот, в длинноволновую при увеличении отношения длин экваториальной и полярной осей.

ЗАКЛЮЧЕНИЕ

В настоящей работе показана возможность изготовления на основе композитного материала с металлическими наночастицами светопоглощающего покрытия толщиной в несколько микрометров. Несмотря на гладкую (неструктурированную) поверхность такое покрытие способно эффективно захватывать и поглощать излучение в широком диапазоне углов падения. Отражательная способность нанокомпозитного слоя существенно снижена за счет согласования оптических характеристик окружающей среды и нанокомпозита. Подобные покрытия могут использоваться в качестве отражающих фильтров, у которых область перехода между высокой и низкой отражательной способностью контролируется геометрией и концентрацией включений.

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований и Федеральной целевой программы “Научные и научно-педагогические кадры инновационной России на 2009-2013 годы” Министерства образования и науки РФ.