Апостериорная оценка навигационных параметров в спутниковых системах на основе инвариантной модели объекта

В настоящее время в алгоритмах обработки спутниковых измерений при формировании навигационных параметров подвижных объектов используются или различные модификации метода наименьших квадратов, или разнообразные модификации фильтра Калмана [1, 2]. Точность определения параметров движения объекта при использовании последнего оказывается выше, чем в методе наименьших квадратов (МНК), но требует обязательного знания уравнений движения каждого конкретного объекта. Это принципиально затрудняет использование существующих калманов-ских навигационных алгоритмов в подавляющем большинстве подвижных объектов, когда неизвестны ни траектория движения, ни вид физической модели, ни характер действующих на объект возмущений и т. д. В то же время очевидно, что применение методов стохастической фильтрации для обработки спутниковых измерений в самом общем случае их использования позволит значительно повысить точность определения навигационных параметров в силу ухода от различных упрощающих допущений (линеаризации, дополнительной информации об объекте, о помехах и т. п.), используемых в существующих алгоритмах спутниковой навигации.

ПОСТАНОВКА ЗАДАЧИ

Проанализируем принципиальную возможность апостериорного стохастического оценивания по спутниковым измерениям навигационных параметров любых подвижных объектов. Форми- руемые при этом алгоритмы фильтрации должны быть инвариантны к виду физической модели объекта, траектории его движения, характеру возмущений и пр. Так как существо предлагаемого подхода не зависит от вида используемого режима спутниковых измерений, то рассмотрим далее только автономный режим (как наиболее широко применяемый) и соответственно только кодовые и доплеровские измерения спутниковых навигационных систем (СНС). При этом решение поставленной задачи рассмотрим для СНС с высокой частотой поступления навигационных сообщений, позволяющей считать характер спутниковых измерений по отношению к динамике изменения навигационных параметров объекта непрерывным. (Частота приема спутниковых сообщений в отдельных приемниках GPS уже составляет 20 Гц, к концу 2012 г. — до 100 Гц с последующим ее увеличением [3]).

В стандартном (автономном) режиме информационный сигнал кодовых измерений (псевдодальность) в общем случае может быть записан как [1, 2]:

Z r = 7 (5 - 5 )² + (п - n )² + (Z c - Z ) 2 + W z_r , (1)

где ξ_c , η_c , ζ_c — известные координаты спутника в гринвичской СК (ГСК); ξ , η , ζ — текущие координаты объекта в ГСК; W_Z — белый гауссовский шум (БГШ) с нулевым средним и известной интенсивностью D_Z ( t ), обусловленный алгоритмически нескомпенсированными ошибками часов спутников и приемника, задержками сигнала при прохождении ионосферы и тропосферы, ошибками многолучевости и другими погрешностями.

В свою очередь информационный сигнал доплеровских измерений (псевдоскорости) Z_V в автономном режиме может быть представлен следующим образом [1, 2]:

z_v = [ & - z )(V ₅ C - v , ) + (П с - n ) ( V c - V ) +

+ (Z c - z )( V z c - V z ) ]x

x ( V ( Z c - Z ) 2 + (n c - n ) 2 + (Z c - Z ) 2 ) " ' + W z v , (2)

где V _{ξ c} , V _{η c} , V _{ζ c} — проекции вектора скорости спутника на оси ГСК; V _ξ , V _η , V _ζ — проекции вектора скорости объекта на оси ГСК; W_Z — БГШ с нулевым средним и известной дисперсией D_Z ( t ), обусловленный погрешностями измерения.

Очевидно, что сигналы кодовых и доплеровских измерений несут информацию как о текущих координатах объекта, так и о его скорости, т. е. могут быть непосредственно использованы при синтезе алгоритмов фильтрации навигационных параметров.

ИНВАРИАНТНАЯ НЕПРЕРЫВНАЯ МОДЕЛЬ ИЗМЕНЕНИЯ НАВИГАЦИОННЫХ

ПАРАМЕТРОВ ОБЪЕКТА

Для возможности теоретически строгого решения задачи апостериорного оценивания вектора состояния объекта необходимо прежде всего иметь его уравнения состояния, записанные в стохастической дифференциальной форме Ланжевена (причем в соответствии с вышеизложенным инвариантные к виду физической модели объекта, характеру его движения и виду действующих на него возмущений). Для решения этой задачи рассмотрим предварительно уравнение (2). Относительно вектора скорости объекта его можно переписать в виде

[ ( Z c - Z V + ( П с - n )V n c + ( Z c - Z ) V z c ]-

-V ( Z c - Z )² + (n c - n )² + ( Z c - Z )² x ( Z v - W z v ) =

= ( Z c - Z ) V z + (n c - nV + (Z c - Z ) V z             (3)

или в векторной форме

( s c - s )^T V c - [ ( s c - е ) Т ( е c - s ) ] 2 ( Z v - W z v ) =

= ( s c - s )^T V ,                                       (4)

где ^s c = ( ^Z c , n c , ^Z c ) ^Т, ^s = ( ^Z, n, ^Z f-

Очевидно, что для определения всех компонен- тов вектора скорости объекта V = s приведенного уравнения, полученного по доплеровским измерениям одного спутника, недостаточно. Для формирования недостающих уравнений предварительно введем следующие обозначения:

s _ci = ( Z_c, , n_c, , Z_c ,) , i = 1,2,3,— вектор известных координат i -го спутника в ГСК,

^V ci = ( ^V , ^V n ci , ^V Z ci ) ^Т — вектор скорости i ^-го спутника в ГСК,

Z Vi — сигнал доплеровских измерений i -го спутника, W_Z — погрешности доплеровских измерений i -го спутника.

Для возможности определения вектора скорости объекта V = s запишем систему уравнений, аналогичных (4), но построенных уже по доплеровским измерениям трех спутников:

^{( s} c , ^{- s ) T} V c , ^- [ ^{( s} c ^{- s ) T ( s} c , ^{- s} ) ] 2 ^{x x} ( Z v ^- W z_V , ) = ^{( s} c , ^{- s )T s} ,

^{( s} c ₂ ^{- s )T} V c ₂ ^- [ ^{( s} c ₂ ^{- s )T( s} c ₂ ^{- s} ) ] 2 ^x

^x ( ^Z V ₂ ^{- W} Z_{V 2} ) = ^{( s} c ₂ ^{- s )T s} ,

^{( s} c 3 ^{- s )T V} c 3 ^- [ ^{( s} c 3 ^{- s )T( s} c 3 ^{- s} ) ] 2 ^{x x} ( ^Z V 3 ^- W Z v 3 ) = ^{( s} c 3 ^{- s )T s} .

Обозначив далее для сокращения записи

[ ( s c i - s )^T( s c i - s ) ]2 = p i , i = 1,2,3;

p (s_c , s_c , s_c , s ) = с ₁ с ₂     с ₃

ρ 1 0

0 ρ ₂

ρ ₃

^Z V 0 =

Z V 1

Z V 2

Z V 3

W

Z_{V 0}

W

Z V 1

W

Z_{V 2}

W

Z V 3

опишем полученную систему уравнений в матричном виде:

( s c , - s )^T V c ,

(s_c - s )^T V_c с ₂              c ₂

^- P ^{( s} c , , ^s c ₂ , ^s c ₃ , ^{s ) Z} V 0 ⁺

(s_c - s )^T V_c с ₃                c ₃

•

+р <£с , £ , £ , £) Wz с1 с2    с3            ZV0

( ε с 1	— £ ) Т
( ε с 2	— £ ) Т
( ε с 3	— £ ) Т

ε .

Данная система легко допускает разрешение относительно вектора скорости объекта V = £ :

—

—

—

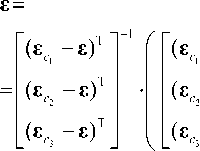
ε )^Т V c ₁

ε )^Т V c ₃

ε )^Т V c ₂

—

А (6)

— р ( £ , £ , £ , £ ) Z_{v 0} + р ( £ , £ , £ , £ ) W_z с ₁ с ₂ с ₃            V 0              с ₁ с ₂ с ₃              Z_{V 0}

У

^£ 0 = ^{£ (0)},

( ε с ₁

—

ε )^Т

1—1

где

( ε с ₂

—

ε )^Т

^{( £} с 3 ^{— £ )} Т

ратная матрице

= Ф ( £ с 1 , £ с 2 , £ с 3 , £ ) — матрица, об-

^{( £} с , ^{— £ )Т}

(£_с — £ ) Т с ₂

^{( £} с 3 ^{— £ )Т}

(см. Приложение 1).

Полученные уравнения описывают динамику изменения только вектора координат объекта, в то время как в большинстве практических приложений требуется оценить еще и его скорость.

Для синтеза уравнений линейной скорости объекта уравнения (6) запишем в следующем виде

по времени. При этом откажемся от предположения возможности представления вектора помех доплеровских измерений в виде БГШ, заменив его на допущение возможности более точного описания данного вектора системой нелинейных стохастических уравнений в форме Ланжевена:

^W , v о = ф ( W V ₀ , t ) + S ,             (7)

где φ ( W _Z , t ) — известная нелинейная вектор-функция, ς — центрированный БГШ с известной матрицей интенсивности D _ς , что справедливо при предварительной калибровке приемника (например, для спутниковых приемников специального назначения). Дифференцируя приведенные выше уравнения, имеем:

.                                                                                                        .             .             .

V = о ( £ , £ , £ , V , V , V , V , V , V , с ₁ с ₂ с ₃ c ₁ c ₂ c ₃ c ₁ c ₂ c ₃

•

W Z V ₀ , ^Z V 0 , ^Z V 0 , ^£ , ^{V ) +}

+ ФЕ (£с,,£с2 ,£с3 , £)Р (£с1 ,£с2 ,£с3,£) ^.

Вид вектор-функции .             ..

θ(ε ,ε ,ε ,V ,V ,V ,V ,V ,V ,W  ,Z с1    с2    с3     c1     c2     c3     c1     c2     c3      ZV 0

Z _{V 0}, ε , V )

и вывод уравнений (8) приведены в Приложении 2.

Для возможности синтеза алгоритмов апостериорной оценки вектора скорости V объекта, зависящего, как видно из (8), от вектора координат объекта ε , необходимо построить единую систему уравнений вектора состояния объекта, объединив системы уравнений (6), (8) и дополнив их уравнением (7) вектора помех доплеровских измерений:

£ = Ф_£ ( £ , £_с , £_с , £ ) 1В(£_с , £_с , £_с , V_c , V_c , V , £ ) — ε с ₁ с ₂ с ₃                с ₁ с ₂ с ₃ c ₁ c ₂ c ₃

1^ с

—

ε )^Т V c ₁

•.

^— Р ^{( £} с , , ^£ с 2 , ^£ с 3 , ^{£ )} Z V 0 ⁺ Р ^{( £} с , ^{, £} с 2 ^{, £} с 3 , ^{£ )} W Z V ₀ } ;

_   .

V = ^Ф _Е ^{( £} с , , ^£ с 2 , ^£ с 3 , ^{£ )}

—

ρ ( ε , ε , ε с ₁ с ₂     с ₃

( ε с ₂

—

ε )^Т V c ₂

—

Ц(^$ с 3

—

ε )^Т V c ₃

, ^{£ ) Z} V 0 ⁺ Р ^{( £} с , , ^£ с 2 , ^£ с 3 , ^{£ )}

W

Z V 0

А

V = о (£_с , £_с , £_с , V , V , V , V , V , V , w_z , с 1     с 2     с 3      c 1      c 2      c 3      c 1      c 2      c 3        Z V 0

•

^Z V 0 , ^Z V 0 , ^£ , ^{V ) +}

^{+ Ф ( £} с 1 ^{, £} с 2 , ^£ с 3 , ^{£ )} Р ^{( £} с , , ^£ с 2 , ^£ с 3 , ^{£ )} ? ;

^W Z V 0 = Ф ( W Z V 0 , t ) + S

^ (9)

У

= Ф (f ,£ ,£ ,е)1В(е ,£ ,£ ,V ,V ,V ,е) ε      с ₁ ,    с ₂ ,    с ₃ ,                 с ₁ ,    с ₂ ,    с ₃ ,     c ₁ ,     c ₂ ,     c ₃ ,

—

или в векторной форме Ланжевена

Y = F ( Y , t ) + F , ( Y ) _S ,

—

ρ ( ε , ε , ε с ₁ с ₂     с ₃

, ^{£ ) Z} V 0 ⁺ Р ^{( £} с , , ^£ с 2 , ^£ с 3

, ε ) W

Z V 0

где Y = [ £ ^Т, V ^t , W _z ; о ] Т , Y o = Y ( 0 ) ,

и продифференцируем обе части данной системы

F 1 ( ^Y ) =

Φ _ε ( ε _{с 1} , ε _{с 2} , ε _{с 3} , Y ) ρ ( ε _{с 1} , ε _{с 2} , ε _{с 3} , Y )

Е 3

F ( Y , t ) =

■ Ф _£ ( E с , e с 2 , e с 3 , Y ) { h ( e с , e с 2 , e с 3 , V , V _c 2 , V c 3 , Y ) -— P ^{( E} с ^{, E} с ₂ , ^E с 3 , Y Z V 0 + P ^{( E} с ^{, E} с ₂ , ^E с 3 , Y ^W Z_{v 0} }

0 ( E с , E с 2 , E с 3 , V. , V _c 2 , V _c 3 , Z v 0 , Z V 0 , Y )

φ ( Y , t )

Е ₃ — единичная матрица размерности 3.

Принципиальными особенностями полученных уравнений (10) являются, во-первых, их общий характер (т. к. при их выводе не было сделано никаких упрощающих допущений о физической модели объекта, характере его движения и виде действующих на него возмущений), а во-вторых, возможность использования на их основе методов нелинейной стохастической фильтрации, обеспечивающих оптимальность оценок навигационных переменных при обработке информации с СНС.

УРАВНЕНИЯ НЕПРЕРЫВНОГО НАБЛЮДЕНИЯ ВЕКТОРА СОСТОЯНИЯ ОБЪЕКТА

С целью использования данной возможности необходимо получить, следуя [2, 4], уравнение наблюдателя за вектором Y (т. е. аналитическую модель сигнала, несущего информацию о компонентах вектора Y ). Для этого воспользуемся сигналами измерения кодовых дальностей (1), которые в общем виде представим как

Z r = 7 Z - Z )² + (П с - n )² + (Z с - Z )² + W z₈ =

= H ( E с , Y ) + W z_r .                          (11)

Анализ наблюдателя (11) показывает, что сигналы измерения даже одного спутника явно зависят от вектора координат объекта (обеспечивают его полное наблюдение), т. е. для теоретически строгого решения задачи апостериорного оценивания координат объекта достаточно измерений кодовых дальностей, полученных от одного спутника. Но т. к. для формирования вектора состояния объекта все равно необходимо наличие измерений с трех спутников, то целесообразно для увеличения информативности наблюдателя использовать при синтезе уравнений наблюдения также измерения кодовых дальностей с трех спутников.

В этом случае размерность наблюдателя увеличивается до трех:

Z r 1 = 7 ( Zd- Z)² + П - n )² + ( Z d - Z )² + W z r 1 =

= H , ( E ., Y ) + W z_r 1 ,

Z r 2 = 7 (Z с 2 - Z )² + ( П с 2 - П )² + ( Z с 2 - Z )² + W z_r 2 = ₍₁₂₎ = H 2 ( E с 2 , Y ) + W z_r 2 ,

Z r 3 = 7 (Z с 3 - Z )² + ( П с 3 - П )² + (Z с 3 - Z )² + W z r 3 =

= H3(E с 3, Y) + Wzr 3, где ZRi — сигнал кодовых измерений i-го спутника, WZ — погрешности кодовых измерений.

Но в данных наблюдениях не содержится в явном виде информация о векторе скорости V объекта. В связи с этим для возможности явного наблюдения вектора скорости объекта V необходимо привлечь доплеровские измерения четвертого спутника Z_V :

Z_v = {( e_c - e ) ^t V_c - (e_c - e ) ^t V} X

V ₄          с ₄             c ₄        с ₄

_ 1

^{X[ ( E} с 4 ^{- E )T( E} с 4 ^{- E ) ]   2 + W} Z v 4 =

= HV4(E с4, Vc4, Y) + WZv 4, где WZ — БГШ с нулевым средним и интенсивностью DZ . При этом измерение кодовых дальностей четвертого спутника ZR целесообразно тоже включить в общий вектор наблюдения, что только повысит его информативность.

Тогда вновь полученный наблюдатель в векторной форме имеет вид:

	г z«a Zr 2		"    H 1 ( E с , Y )   ' H 2 ( e с 2 , Y )		" Wz  " Zr 1 W Z r 2
Z RV =	Z R 3	=	H з ( е с 3 , Y )	+	Wz Z R 3	=
	Z R 4		H 4 ( E с 4 , Y )		Wz Zr 4
	Z v 4		. H V . ( E с 4 , V c 4 , Y ) _		Wz Z V 4

= H RV ( E с 1 , E с 2 , E с 3 , E с 4 , V_c 4 , Y ) + W rv . (13)

Полученное представление уравнений состояния объекта в форме "объект—наблюдатель" (10), (13) позволяет построить для вектора Y апостериорную плотность p_z ( Y , t ) , знание которой, по существу, решает проблему определения любых вероятностных оценок вектора координат Y .

Процедура формирования p_Z ( Y , t ) в общем случае сводится к решению интегро-дифференциального уравнения с частными производными (уравнения Стратоновича), которое в общем случае не имеет аналитического решения. Поэтому в теории нелинейной фильтрации для получения оценок нелинейных процессов вида (10) используют различные приближенные (субоптимальные) методы [4], наиболее известным и востребованным из которых является обобщенный (нелинейный) фильтр Калмана. Его использование, как правило, позволяет достичь необходимого компромисса между требуемой точностью и вычислительными затратами в реальных системах навигации и не встречает никаких принципиальных трудностей как в бортовых вычислителях общего назначения, так и специализированных.

Согласно [4], уравнения (10, 13) в форме "объект—наблюдатель" позволяют записать обобщенный фильтр Калмана для исследуемой НС:

Y = F ( Y , t ) +

+ K ( Y , t ) [ Z RV - H RV ( s ., ® с 2 , S с 3 , S с 4 , V 4 , Y ) ] ,

K ( Y , t ) — R ^{d H R} V ^{( s} с ¹ , ^s с 2 , ^s с 3 , ^s с 4 , V 4 4 , ^Y ) D-. ,

\ /d

RfY - ^dF^{( Y} , t )       +     t^F ^{( Y} , t ) +

R Y, t —----x R Y, t + R Y, t -----x+ dY    \ ) \   )

+ F 1 ( Y ) d F T ( Y ) - к ( Y , t ) d RV K T ( Y , t ) ,

^ (14)

где Y — оценка вектора состояния Y ( t ) , R ( 'Y , t ) — апостериорная ковариационная матрица, 'Y 0 — — M ( Y o ) , R о — M { ( Y o - Y _o )( Y o - Y _o ) T } , D _R v —

D 0000

Z R 1

0 D 000

Z R 2

0  0 D 00

Z R 3

0    0    0 D 0

Z R 4

0    0    0   0   D _Z

Т. к. здесь созвездие спутников содержит m >  3

спутников, то возникает возможность одновременного синтеза С_m ³ различных уравнений координатного вектора объекта, но, кроме этого, еще и С_m ³ различных уравнений вектора скорости объекта. При этом вектор наблюдения содержит кроме m измерений кодовых дальностей еще и доплеровские измерения с оставшихся спутников, не использованные при синтезе уравнений состояния объекта. Это приводит к возможности параллельной реализации большого числа нелинейных фильтров, выходные оценки которых могут быть дополнительно обработаны известными статистическими методами (например, робастного оценивания) с целью еще большего повышения точности решения навигационной задачи.

По сравнению с применяемым в настоящее время для вторичной обработки спутниковой информации МНК [1, 2] предложенные алгоритмы обладают всеми известными преимуществами фильтра Калмана перед ним, вытекающими из дополнительного использования уравнений движения объекта и независимости от особенностей градиентной матрицы измерений, что позволяет повысить в целом точность определения параметров движения наблюдаемого объекта.

ПРИМЕР

Для иллюстрации эффективности предложенного подхода было проведено моделирование алгоритма фильтрации (14) на временнóм интервале t е [ o;iooo ] (с) с шагом A t = o.oi с методом Рунге—Кутта 4-го порядка. Движение объекта задавалось по локсодромической кривой с азимутальным углом 45 ° из точки с долготой 3o ° , широтой 45 ° , s _o — ( 2 254 963.52, 4 5o9 927.o5, 3 9o5 711.39 ) ^Т(м) и законом изменения проекции скорости объекта на плоскость меридиана V М = 10 (1+sin 0.005 t ) (м/с) .

В качестве модели помех измерений был использован аддитивный гауссовский вектор-шум с нулевым мат. ожиданием и интенсивностью для кодовых измерений — (10 м)2, доплеровских измерений — (0.25 м/с)2. По окончании временнóго интервала моделирования максимальные ошибки компонентов навигационного вектора составили

A ^ — 3.4 м, A n — 4.2м, A Z — 3м, A V , — o.45 м/ с,

AV — o.14 м/ с, AVZ — o.34 м/ с, что свидетельствует о возможности весьма эффективного практического использования предложенного подхода.

ПРИЛОЖЕНИЕ 1

При обозначениях

( Z Ci- Z ) - Z i , ( П C i

-n)-ni,(ZCi-Z)-Zi, i = 1,2,3, матрица Φ(εс ,εс ,εс ,ε) имеет вид

^{Ф ( £} C 1 , ^£ C 2 , ^£ с 3 , ^£ ) =

= { z , ( n ₂ Z ₃ - n.z ) - пД 2 Z 3 - Z 3 Z 2 ) + Z 1 ( Z 2 П 3 - ^ з П 2 ) }^{- 1} X

n 2 Z 3   n 3 Z 2       n 1 Z 3 + n 3 Z 1 X Z 3 Z 2 - Z 2 Z 3     - Z 3 Z 1 + Z 1 Z 3 _ Z 2 П 3 - Z 3 n 2    - Z 1 n 3 + Z 3 П 1

n 1 Z 2 - n 2 Z 1 1 Z 2 Z 1 - Z 1 Z 2 Z 1 n 2 - Z 2 П 1 j

ПРИЛОЖЕНИЕ 2

При обозначениях

Q - ^. C1 Sc 2 ε , Q'- sc .C1 ^^ с 2 Sc , c = \V= 1 C1 VC2 , c'- \'Ve C1 Vc с2 с3 с3 • VV-3 J V S S с3 процедура дифференцирования уравнения вектора скорости такова:

. |д Ф ( £ , £ , £ , £ ) A J _f

^{V £          C 3} ^ ^W C 1 , £ C 2 , £ C 3 , ^У . , VC 2 , V 3 , E ) - P ( £ C 1

, £ , £ , £) Zy0 + p (£ , £ , £ , £) Wz  1 + с2   с3         V 0          с1 с2   с3           ZV 0

+ Ф_£ ( £ , £ , £ , £> ε с ₁ с ₂ с ₃

б E(£_c , £ , £ , V , V , V , £ ) с ₁ с ₂     с ₃      c ₁      c ₂      c ₃

a

Q c

®

Q '

c

-

(^{д p ( £} c i, ^£ c 2 , ^£ c 3 , ^{£ )} a )

(     d Q      ® ^{Q Z} V ⁰

-

- P ^{( £} с 1 , ^£ с ₂ , ^£ с ₃ , ^{£ ) Z} V 0 ⁺

( ^d P ^{( £} C 1 , ^£ C 2 , ^£ C 3 , ^{£ )} _v a q

ˆ

•

® Q ' W_z  + p ( £ , £_c , £_c , £ ) W_z

Z V 0           с 1 с 2     с 3           Z V 0

( д Ф (£_c , £_c , £_c , £ ) a ------^C 1’ ^C 2’ ^{C 3}’ ' ^

( д Q

' c 1)

^V J j

{ ^{B ( £} C 1 , ^£ C 2

, £c , Vc , Vc , Vc , £) - p (£c , £c , £c , £) Zv0 + p <£c , £c , £c , £) Wz  1 + с3      c1      c2      c3                  с1    с2    с3           V 0             с1    с2    с3             ZV 0

^{+ Ф} s ^{( s} с 1 , ^s с 2 , ^s с 3 , ^{s )} ‘

a s ( s , £_с, £_с, V , V , V , s ) с ₁ с ₂     с ₃      c ₁      c ₂      c ₃

д

Q с

®

с

V

с

—

'^д P ^{( s} с , , ^s с 2 , ^s с 3 , ^{s )}

к

д Q

®

с

V

1 \

^Z V 0

J )

^— P ^{( s} с 1 , ^s с 2 , ^s с 3 , ^{s ) Z} V 0 ⁺

( д p (£_c , £_c , £_c , s ) „ ^с 1     ^{с 2 с 3}        ®

к д Q

с

V

1\

л)

W_z  + p ( s , s , s , s ) (ф( W_z , t ) + s) ' =

Z V 0             с 1 с 2     с 3                  Z V 0

•

•

= 0 ( s , s , s , V , V , V , V , V , V , W_z , Z_{v 0}, Z_{v 0}, s , V ) + Ф_£( s , s , s , s ) p ( s , s , s , s ) s , с ₁     с ₂     с ₃       c ₁       c ₂       c ₃       c ₁       c ₂       c ₃        Z_{V 0}       V 0      V 0                     ε     с ₁      с ₂     с ₃              с ₁      с ₂      с ₃

где ® — знак блочного произведения матрицы на вектор. Здесь производная матрицы

χ ₁

Л= [ Л ₁ Л ₂ „. Л m ] , где Л i — i -й столбец матрицы, по вектору х =

χ ₂

, где χ_i — i -й элемент вектора,

χn имеет следующую блочную структуру:

алГал, дл2 ^ дЛт дх _ дх дх    дх а блочное произведение матрицы на вектор — соответственно дЛ

— ® х = д х

^ х

L д х

дЛ

2 χ д х

дЛ т • д х ^х

.