Апостериорная оптимизация псевдоградиентной процедуры оценивания межкадровых деформаций изображений

При псевдоградиентном оценивании параметров изображений характер сходимости оценок и вычислительные затраты зависят от объема локальной выборки отсчетов изображений, используемой для нахождения псевдоградиента. Рассмотрено несколько алгоритмов апостериорной оптимизации объема локальной выборки при оценивании межкадровых геометрических деформаций изображений, способствующих выводу псевдоградиентной процедуры из локальных экстремумов целевой функции.

Перспективным направлением [1] при оценивании параметров межкадровых геометрических деформаций изображений (МГДИ) является использование псевдоградиентного подхода. Псев-доградиентную процедуру (ПГП) в общем виде можно записать как [2]:

где а - вектор оцениваемых параметров преобразования изображения Z(1) в изображение Z(2), задающий геометрические деформации изобра- жения Z(1); t = 1, T, - номер итерации; Лt - матрица усиления, et (•) - псевдоградиент целевой функции (ЦФ) J(-), характеризующей качество оценивания. В ПГП оценивания МГДИ псевдо- градиент βt находится по локальной выборке Zt объема ц , представляющей собой отсчеты z(2 деформированного изображения Z(2), попавшие в локальную выборку на t-й итерации, и отсчеты ~ (i) 2

z jt, at-i , взятые из некоторого непрерывно го изображения Z(1), полученного из Z(1) (например, оцениванием или интерполяцией), где jt е Q -jt eQ - - координаты отсчетов z(^); Q -jt -план локальной выборки на t-й итерации.

Псевдоградиентные процедуры применимы к обработке изображений в условиях априорной не-определенности,предполагаютнебольшие вычислительные затраты и не требуют предварительной оценки параметров исследуемых изображений. Формируемые ими оценки устойчивы к импульсным помехам и сходятся к оптимальным значениям при довольно слабых условиях. Недостатком ПГП при обработке реальных изображений является наличие локальных экстремумов оценки ЦФ, характеризующей качество оценивания, что в процессе сходимости оценок на отдельных реализациях существенно замедляет скорость сходимости или даже может привести к ее срыву. Характер сходимости оценок и вычислительные затраты во многом определяются объемом локальной выборки (ОЛВ) отсчетов изображений, используемом на различных итерациях оценивания для нахождения псевдоградиента ЦФ.

Оптимальный по заданному критерию ОЛВ, рассчитанный априорно [3], обеспечивает выполнение этого критерия лишь в среднем. При конкретной реализации изображения оценка ЦФ кроме глобального экстремума может содержать еще и множество локальных экстремумов. Последние могут быть вызваны, например, коррелирован-ностью отдельных протяженных объектов на изображении и проявляются, если большая часть отсчетов локальной выборки попадает в эти области, т.е., в конечном счете, обусловлены ограниченностью ОЛВ. Поэтому увеличение объема или замена локальной выборки Z_t способствует выводу ПГП из локального экстремума. Таким образом, на каждой итерации оценивания целесообразна проверка признаков локальных экстремума ЦФ, а при их наличии - увеличение объема или смена локальной выборки. При этом ОЛВ становится адаптивной величиной. Поэтому целесообразно найти признаки локальных экстремумов ЦФ и на их основе синтезировать процедуры оценивания параметров МГДИ, в которых ОЛВ в ходе выполнения процедуры автоматически адаптируется на каждой итерации.

Рассмотрим несколько подходов к построению ПГП оценивания параметров МГДИ, в которых ОЛВ μ в ходе выполнения процедуры автоматически регулируется (адаптируется) на каждой итерации. В этих алгоритмах очередная итерация оценивания параметра осуществляется при выполнении некоторого условия. Если при минимальном для выполняемой итерации ОЛВ условие не выполняется, то ОЛВ μ последовательно увеличивается до тех пор, пока условие не будет выполнено. Таким образом, для каждой сложившейся на данной итерации локальной выборки ее объем минимален для удовлетворения условия выполнения итерации. Если задача оценивания параметров МГДИ является частью задачи идентификации, то для достижения требуемой доверительной вероятности идентификации может потребоваться большой ОЛВ М ид , который не оп-

- равдан в процессе сходимости оценок а . В этом случае при адаптивном регулировании ОЛВ в качестве его максимального значения цтах можно выбрать цmax = цид. Тогда достижение цmax одновременно будет означать и решение задачи идентификации.

Для нахождения численных величин, применяемых в условиях выполнения итерации, будем использовать значения оценок ЦФ, найденные по локальной выборке. Введем также следующие обозначения: qt (Mt) = q(zt, Mt) - оценка значения ЦФ на t итерации, вычисленная по от- z?(1) (jt, at-i) локальной выбор-

2) _ счетам z ^xt_t и

ки объема Mt; q± (Mt) - оценка значения ЦФ на вычисленная по отсчетам z(M и jt

t -ой итерации, „X - ^

z ± ¹⁾(j t , a i, t - i , ... a i , t - i ±A _ai , ... a m,_t - 1 ) , то-есть при задании оценке параметра α _i некоторого положительного (отрицательного) приращения.

В первом примере алгоритма адаптации ОЛВ зададим следующее условие выполнения очеред-нойитерациинахожденияоценки a i , t + 1 параметра α _i . Итерация не выполняется, а ОЛВ μ_{t min} увели-чиваетсянаединицу(влокальнуювыборкудобав-ляется новая пара отсчетов _z^ и z ⁽¹⁾ ( j t , a _t - i ) ), если на очередной t -й итерации оценка q t (м m i n ) ЦФ при локальной выборке объема ^μ t min больше некоторого критического значения q _Kp . Затем это условие проверяется с увеличенным на единицу ОЛВ ( M t min +1). Если оно вновь выполняется, то ОЛВ увеличивается еще на единицу и т.д. вплоть до значения M max • Если же при некотором ОЛВ условие не выполняется, то очередная, ( t + 1 ) -ая итерация формирования оценки a i , _{t + 1} параметра a i при псевдоградиенте Ду _{+ 1} формируется в соответствии с правилом ^e i , t + i = sgn ⁽ q + ( Mt ) “ q t ( M t ) ) . Процедуру оценивания параметра МГДИ в этом случае можно записать как

2    2

^a i , t + 1     ^a i , t     ^ t + 1 ^в i , t + 1 ⁽ M t ) ;

⎧⎪_⎨ μ k + 1, ⎪⎩ ^μ k ^,

если qt (Mk) ^ qKp, в другом случае;

Av+i = sgn (qt (Mt)- qt (Mt)), где k = 0,(kmax - kmin) .

Экспериментальные исследования показали, что в ПГП целесообразно также ввести дополнительно условие, обеспечивающее увеличение ОЛВ, если q t ( мк ) больше обоих значений q t ( м к ) и q t ( я к ) . Тогда

( q t ( ^ k ) ^ q^ ) или

μ _t =⎨

μ _k +1, если

jqt U) > qt (A))л (qt U) > qt (мj)

⎪⎩μ _k ,      в другом случае .

На рис. 1 приведены усредненные по 250 ре- ализациям экспериментальные зависимости рассогласования £hx = hxt - h от числа итераций. Кривая 1 соответствует результатам, полученным с помощью ПГП (2), а кривая 2 получена при пос тоянном μ = μcp , где μcp = ∑ μk - средний ОЛВ k =1

при изменении t от 1 до 2000. При небольшом числе итераций наблюдается даже проигрыш в точности оценивания (на 50 итерации примерно в 1,1 раза), что объясняется большей скоростью сходимости алгоритма с постоянным ОЛВ на начальных итерациях за счет в среднем большего ОЛВ. Однако при равных вычислительных затратах (к 2000 итерации) обеспечивается выигрыш в точности уже приблизительно в 4,6 раза. При этом ОЛВ ^μ t при больших рассогласованиях оценки сравнительно небольшой (для отношения сигнал/шум g = 100 при t = 10 – примерно 4,2; при t = 500 – примерно 4,4). С ростом числа итераций t в среднем монотонно увеличивается, достигая при t = 2000 примерно 10,2. В эксперименте использовалось реальное изображение оптического диапазона с радиусом корреляции, равном примерно 5 шагам сетки отсчетов. Оценивался вектор параметров МГДИ, включающий угол поворота ϕ = 0 ^o , параллельный сдвиг h = ( h x = 10, h y = 0.4 ) T и коэффициент масштаба κ = 1 при параметрах ПГП: элементы матрицы Л t : X ht = X x = X hyt = 0.1 , Л кt = 0.15/ ( 1 + 0.05 t ) , 4 t = 8 o /( 1 + 0.05 t) , приращения по параметрам МГДИ: A hxt = A hyt = Л_ы , A k t = Л к t , А _ф t = Л _ф t ,

μ min = 2, μ max = 10, q кр = 0,97, q ид = 0.995, t = 1, 2000 . Деформированное изображение дополнительно зашумлялось независимым гауссовским шумом с нулевым математическим ожиданием.

Таким образом, при равных вычислительных затратах предложенная ПГП с регулируемым ОЛВ позволяет существенно увеличить скорость сходимости оценок параметров МГДИ по сравнению с ПГП с постоянным ОЛВ.

Недостатком рассмотренной ПГП является то, что при оценивании нескольких параметров МГДИ в пределах одной итерации локальная выборка формируется отдельно для каждого оцениваемого параметра.

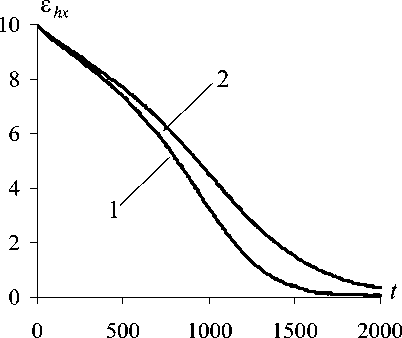
Рис. 1. Зависимость ОЛВ ПГП (2) от числа итераций

Рассмотрим процедуру, при которой независимо от числа параметров ОЛВ за итерацию формируется один раз. При этом воспользуемся результатами работы [4], в которой исследовано три способа вычисления псевдоградиента ЦФ. В первом используется оценка производной ЦФ через приращение оцениваемого параметра, что использовано в рассмотренном выше алгоритме. Второй способ основан на аналитическом дифференцировании ЦФ и приближении производных по яркости конечными разностями. Он применим при известной модели МГДИ, но тоже не позволяет однозначно сформировать ОЛВ. Третий способ использует нахождение полной производной ЦФ через приближение производных по координатам конечными разностями:

Pt = z j∈Ωt

d J( a, Z) dx(j,, a) d J( a, Z,) dy(j, a) ⎜⋅+⋅⎟ ⎜⎝∂x∂α∂y∂α⎟⎠ т/л?          TT где ------® jxt"jyt+1-------jxt, jyt -1 ■ При за- djy (jt, a)

данной модели МГДИ оценки производных dx(jt, a)    dy(j t,a)

^t и         можно найти по модели. В

∂α частности, для аффинной модели получаем:

^dx ( j_t , ^a )

_дк ~ ( j xl ^- j xo ) cos Ф - ( b yl - j y0 ) sin Ф , ^d y ( d K ^a ) ” ( j xl - ^j x 0 ) sin ^ ⁺ ( b yl - ^j y 0 ) cos ^ , ^" ( d^ ) ~ ^K ( ( j xl - ^j x 0 ) sin ^ ⁺ ( b yl - ^j y 0 ) cos ^ ) , d y ( j., a )

—----- » ^K ( ( id ^- j x o ) cos Ф ^- ( b yl ^- j_y 0 ) sin Ф ) ,

∂ϕ где j0 – заданный центр поворота. Тогда для нахождения βt остается найти только

Jx( a, Zt)2 J( а' Zt>и Jy( а, Z)-a J( “-Z) dx                       dy по одной и той же локальной выборке.

РассмотримпримералгоритмаадаптацииОЛВ для ПГП идентификации фрагмента на изображении с оцениванием параметров его местоположения, основанного на третьем способе и использующего в качестве ЦФ выборочный коэффициент межкадровой корреляции. Зададим следующее условие выполнения очередной итерации уточнения оценке а t вектора а . Итерация не выполняется, а ОЛВ M t min увеличивается на единицу в одном из двух случаев:

• а) на очередной t -ой итерации

q + (м) - q X (Mt) =q+(Mt) - q y Cm)=0, где q±(y) (mi) - оценка значения ЦФ на t-й ите- рации, вычисленная по отсчетам  z (22

z^ ( j t , h x(y),t - i ± i, a t - i ).

и

б) оценка

μ

¹X z z г

μl qt =-----------

^^^^^^^B

μμ

X =T X z ?'

^ l = 1        l = 1

2 2

T z 1 T z 2

больше некоторого порогового значения qkp, где zl(1) = ^(i)(jl, j0,at-1) - l-й отсчет изображения Z(1) в локальной выборке Z, t,.

Второе условие при q t Vt = М max ) - q ug обеспечивает идентификацию фрагмента. Если q t См ^М max ) <  q ug , то набирается новая локальная выборка. Если условия не выполняются, проводится очередная, итерация формирования вектора оценок at с ^e t = ^{( e} hx , ^e hy , ^в к , ^в _Ф ) T , где:

^e hx , t = sgn ⁽ q + ( ^ t ) - q X ( ^ t ) ) , ^e hy , t = sgn ⁽ q + ( ^t ) - q y ( ^t ) ) ,

⎛

β _κ = sgn _⎜ ^⎜ ∑ ⎜ β _{hx , t} ⋅

⎝ j ∈ Ω _t ⎝

⎛⎛

β _ϕ = sgn _⎜ ^⎜ ∑ _⎜⎜ β _{hx , t} ⋅ ⎝ j ∈ Ω _t ⎝

x jt , ^a V_R   Mjt , ^a ) )

+ β hy,t ⋅⎟

∂κ                ∂κ⎠ ⎟

⎠

У jt . ^a ).,,      ^d- >'( ^j. ^a ) )

∂ϕ     + βhy,t ⋅     ∂ϕ⎟⎟

⎠

,

.

Таким образом, ^a t = ^at-i^{- л}, ^et ( M t ) ;

для ПГП можно записать

( q, ( M k ) >  qkp) V ( ( M t <  M max ) a

μk+1, если ⎨

μ _t =⎨

⎩ μ _k ,    в другом случае;

На рис. 2 приведена усредненная по 250 реализациям экспериментальная зависимость ОЛВ ^μ t от числа итераций, полученная с помощью ПГП (3). Оценивались параметры МГДИ: h = ( h x = 4.8, h y = 5.1 ) T , ф = 10 o и к = 1.12 при

^ min =3, M max =200, q kp =0,97, q^ =0,995, A hxt =A hyt = 1 , T = 2000 , 2 hxt = \yt = 0.04 , Z _{K t} = 0.001 , Х _фt = 0.17 o , g =100. Видно, что на начальном этапе оценивания ОЛВ в среднем сравнительно небольшой, а с ростом t монотонно увеличивается, достигая при t =2000 примерно 150.

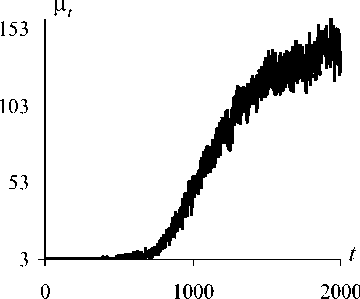
Рис. 2. Зависимость ОЛВ ПГП (3) от числа итераций

Погрешность оценок параметров, полученных с помощью ПГП (3), сравнивалась с погрешностью оценок, полученных при ОЛВ, обеспечи- вающем заданную доверительную вероятность идентификации (в данном случае ц = 200). Анализ результатов показал, что как при адаптивном ОЛВ, так и ОЛВ ц = 200). Для достижения суммарной погрешности, равной 0.4, требуется примерно 2000 итераций. Однако в первом слу-2000

чае ОЛВ всех итераций составляет

X ^ t « 1.2 - 10 5 ,

t =1

что позволило

во втором - Х ^ ^ = 200 ) ~ 4 ' 10 5 ,

t=1

примерно в 3,3 раза сократить вычислительные затраты.

Априорно рассчитанные, оптимальные по некоторому критерию ОЛВ, обеспечивают выполнение этого критерия лишь в среднем. Для конкретной реализации изображения ЦФ качества оценивания, кроме глобального экстремума, может содержать еще и множество локальных экстремумов, вызванных, например, наличием на изображении областей протяженных объектов. Поэтому на каждой итерации оценивания целесообразна проверка признаков локального экстремума ЦФ, а при их наличии - увеличение объема или смена локальной выборки. Проведенные исследования показали, что предложенный подход к апостериорной оптимизации ОЛВ ПГП оценивания МГДИ позволяет существенно со- кратить вычислительные затраты по сравнению с ПГП с постоянным ОЛВ.

Работа выполнена при поддержке РФФИ (грант 07-01-00138-а).

• 1.    Ташлинский А .Г. Псевдоградиентное оценивание пространственных деформаций последовательности изображений // Наукоемкие технологии, Т. 3, № 3, 2002. – С. 32-43.

• 2.    Цыпкин Я З. Информационная теория идентификации М.: Наука. Физматлит, 1995. – 336 с.

• 3.    Самойлов М. Ю. Оптимизация процедур псев-доградиентного оценивания параметров межкадровых геометрических деформаций изображений // Радиолокация, навигация, связь. Труды XII МНТК. Воронеж: Саквоее, 2006. – С. 162-167.

• 4.    Минкина Г. Л. Выбор целевых функций при псевдоградиентном оценивании межкадровых деформаций изображений // Тезисы докладов ВНТК «Информационно-телекоммуникационные технологии». М.: МЭИ, 2004. – С. 24-26.