Аппаратная реализация двумерного параллельно-рекурсивного КИХ-фильтра

yfn^np = Jo \ (,fJ8>6DkX (П. " П= - ”=)•              <1)

гдеу(п.п)- отсчет выходного изображения в точке с координатами 1    2

(п,. п2) ;

Dk - прямоугольная область суммжрования для к-го параллельного звена фильтра;

К - число параллельных звеньев.

Рекурсивная организация суммирования по областям Dk подразумевает, что устройство должно работать как часть конвейерной вычислительной системы обработки изображений (например, такой, какая описана в [4]). Отсчеты входного изображения подаются на вход устройства последовательно, и на каждый поступивший отсчет вычисляется одно значение выходного изображения.

Реализуемый таким образом ПРФ может содержать К структурно идентичных устройств, вычисляющих суммы по областям Dk (параллельные звенья), и арифметический блок, выполняющий взвешенное суммирование выходных отсчетов паралелльных звеньев. Арифметический блок, в свою очередь, состоит из К умножителей на весовые коэффициенты ж сумматора на К входов. Структурная схема такого ПРФ изображена на рис.1.

1*ис. 1. Структурная схема параллельно-рекурсивного фильтра.

Обозначения: 1 - рекурсивные звенья; 2 - умножители на коэффициент; 3 - сумматор

Умножители на весовые коэффициенты и сумматор являются известными устройствами, описание их реализации можно найти, например, в [5, 6]. Поэтому подробно следует остановиться лишь на структуре устройств, реализующих параллельные звенья фильтра. Как показано в [2], суммирование по прямоугольным областям Dk выполняется рекурсивно, раздельно, в два эта-па:

zk(n,.n2) - zjn, - l.n2) + x(n, + i“’.n2) - х(п, + i“'.n2).         (2)

SM(ni>n2> ■ %(",•", - 1) * W, + i’”) - ^„(П^п,* i“*).     (3)

где zk - промежуточная сумма отсчетов исходного изображения по координате п ;

s(n.n) - выходной отсчет звена ПРФ; k 1   2

ikn i^2), i^3), V4)- координаты границ k - окна суммирования (рис. 2).

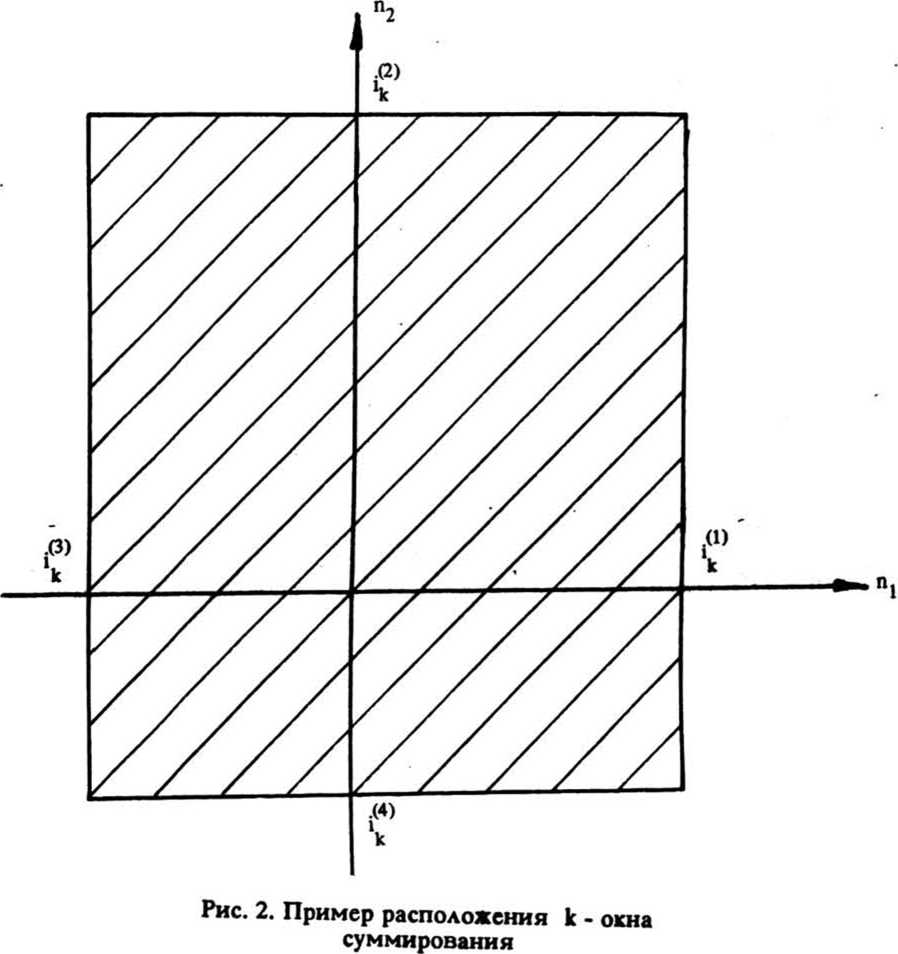
В конвейерной вычислительной системе на вход устройства подается одномерная последовательность отсчетов, полученная построчной разверткой исходного изображения. Пусть длина строки развертки равна L отсчетов, тогда выражения (2) и (3) принимают следующий вид:

zt(n) = zjn - L) + x(n + i^11- L) — x(n + 1"’- L),          (4)

sk(n) + sk(n - 1) + zk(n + i“’) - zk(n + i'*’),               (5)

где zk(n), sk(n) - текущие значения сумм по области Dk> Выражениями (4) и (5) определяется структура вычислительного устройства, изображенная на рис.3. Оно содержит четыре элемента задержки, два сумматора и регистр. Первым сумматором вычисляются отсчеты z^, вторым - отсчеты sk. Элемент задержки 4 обеспечивает подачу на вход сумматора 1 отсчетов входной последовательности с индексами, различающимися на величину L*(ik - ik ),

Вход

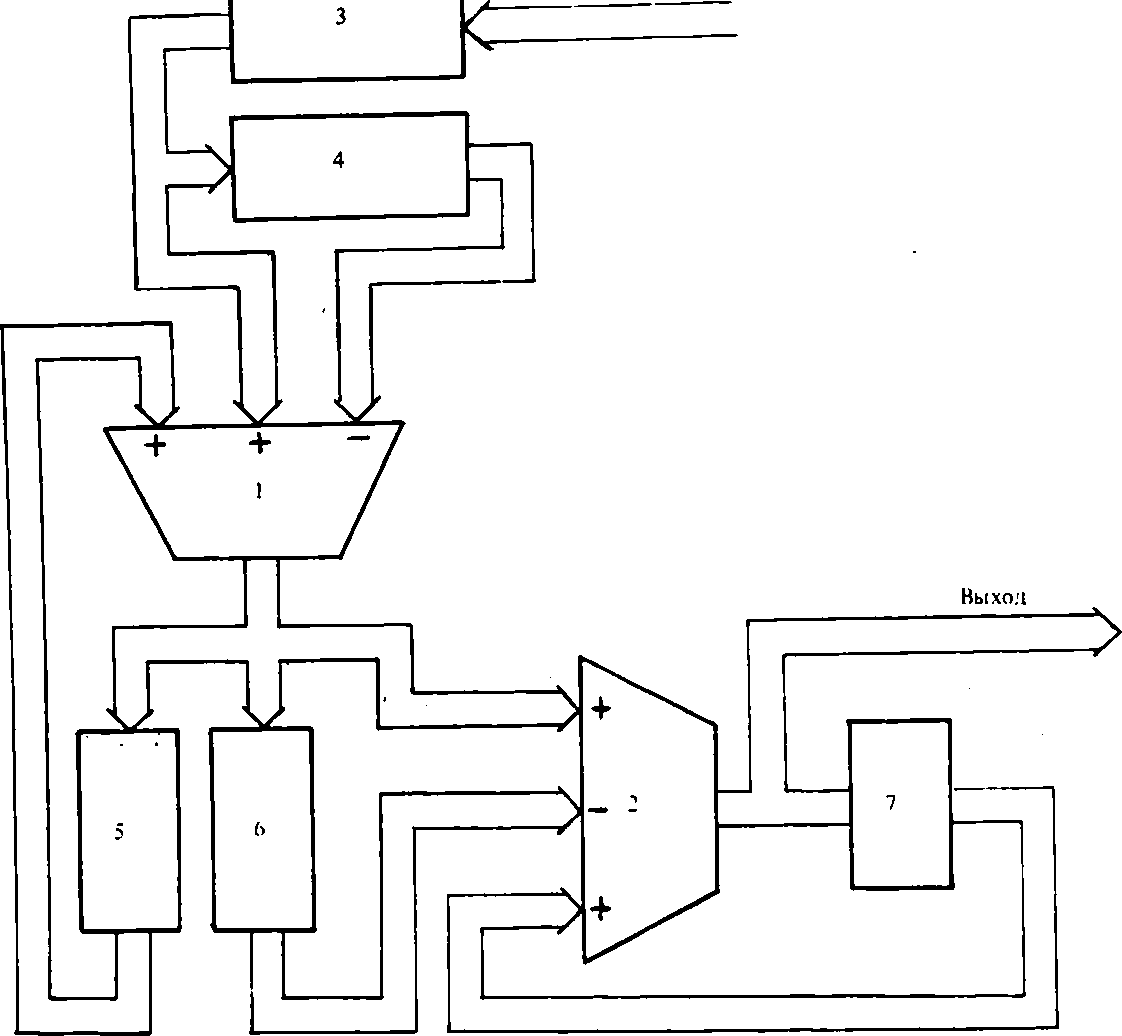
Рис. 3. Структурная схема звена ПРФ. Обозначения: 1, 2 - сумматоры: 3, 4, 5, 6 - элементы задержки; 7 - регистр

а элемент задержки 5 - отсчетов последовательности z , задержанных на строку. Аналогично элемент задержки 6 обеспечивает подачу на вход второго , . (2) сумматора отсчетов zk с индексами, различающимися на величину (1 к~ i^4’)» а регистр выполняет задержку последовательности sk на один такт. Для согласования работы звеньев во времени, т. е. для одновременного получения отсчетов sk с одинаковыми номерами на выходах звеньев, введен элемент задержки 3, который обеспечивает запаздывание сигнала х(п) на величину

Р = I-L + J - Vn-L - i/2), к            к

1(1)  .(2)(К = к к предусмотреть

6, а также

где I, J - соответственно максимальные значения величин = 0, ... К - 1).

При разработке ПРФ с изменяемыми параметрами следует возможность регулировки величины задержек в элементах 3,  4, загрузку величин весовых коэффициентов Qv в умножители.

Элементы с изменяемой величиной задержки могут быть выполнены на основе оперативного запоминающего устройства (ОЗУ), например, с использованием интегральных микросхем статического ОЗУ. Структурная схема возможной реализации элемента задержки приведена на рис. 4.

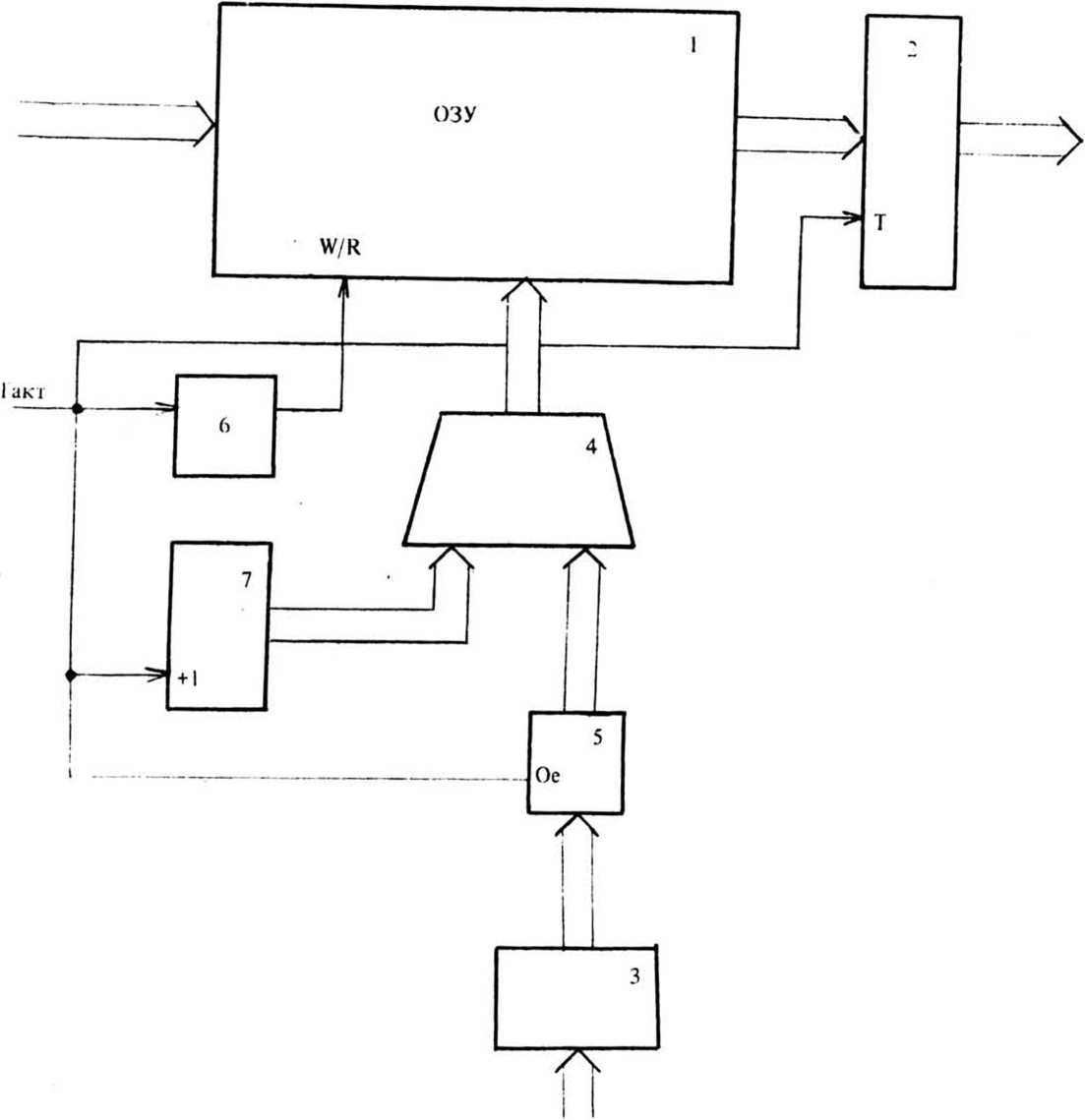
Рис. 4. C i руктурная схема элемента задержки. Обозначения: 1 - блок ОЗУ; 2. з - регистр: 4 - сумматор; 5 - ключ; 6 - одновибратор; 7 - счетчик

Важным достоинством звена ПРФ с прямоугольным базисом является возможность выполнять все вычисления в формате с фиксированной точкой. При этом не требуется округлять результаты арифметических операций, и все вычисления могут быть выполнены без погрешностей. Однако при использовании формата с фиксированной точкой возникает опасность переполнения разрядной сетки сумматоров, что недопустимо из-за значительных искажений выходного сигнала. Оценим длину разрядной сетки первого и второго сумматоров, требуемую для исключения переполнения. Пусть отсчеты входного изображения представлены b-разрядными двоичными числами, а размер окна суммирования не превышает М х N отсчетов.

Максимальное значение входного сигнала в этом случае равно 8-(2ь-1), где 8 - шаг квантования. Максимальные значения сигналов z^ и sk равны соответственно

3(2ь-1)-М       и      8(2b-l)-M-N.

Для их представления необходимо соответственно b = b + < log М >(6)

и b2 = b + < log2M*N > двоичных разрядов,( где знак <С> означает в данном случае ближайшее целое, не меньшее С. Длина разрядного слова данных, хранимых в элементах задержки 3 и 4  (см.

рис.3), равна Ь, для элементов задержки 5 и 6 требуемая разрядность определяется согласно (6), а для регистра 7 - согласно (7).

Сложность аппаратной реализации звена ПРФ, при прочих равных условиях, определяется разрядностью обрабатываемых данных. Объемы ОЗУ, необходимых для реализации элементов задержки 3, 4 и 5, 6, соответственно пропорциональны величинам b и Ь^ Сложность сумматоров также связана с разрядностью слагаемых. Несколько уменьшить сложность аппаратуры можно, выполняя усечение разрядной сетки в различных точках на пути прохождения данных в фильтре. Следует отметить, что в конвейерных системах обработки изображений обычно используется представление данных в одном формате на входе и выходе модулей, что также делает необходимым усечение разрядной сетки данных. В ПРФ усечение длины чисел может быть выполнено по крайней мере в четырех точках: на входе ПРФ, на выходе первого или второго сумматоров звеньев ПРФ и на выходе фильтра. Усечение разрядной сетки на выходе ПРФ не дает какой-либо экономии аппаратных средств и далее не рассматривается.

Очевидно, что любое усечение разрядной сетки данных приодит к появлению погрешности в выходном сигнале ПРФ, которую принято считать аддитивным белым шумом, вносимым в сигнал и имеющим дисперсию [7, 8]:

где 8 - шаг квантования. Для случая, когда уже квантованный сигнал подвергается усечению разрядной сетки, дисперсия дополнительной ошибки оценивается выражением

°кв = 12 (2     1)l                              (9)

где q - количество усекаемых разрядов;

5т - шаг квантования сигнала до усечения разрядной сетки.

При квантовании данных на входе ПРФ оценка погрешности на его выходе может быть получена согласно выражению

: = <• Ei ^2^^' (m , m )€D

1    2

где h(roi>m2) - отсчеты импульсной характеристики фильтра;

- дисперсия ошибки, внесенной квантованием на входе ПРФ и оцениваемой по формуле (8).

При квантовании на входе или выходе вторых сумматоров звеньев ПРФ ошибки, вносимые в сигналы звеньев, можно считать независимыми, поэтому для оценки погрешности на выходе ПРФ воспользуемся выражениями где о"2 и аз - дисперсии ошибок, вносимых усечением разрядной сетки соответственно на входе и выходе вторых сумматоров звеньев ПРФ;

\ - шаг квантования сигнала на входе ПРФ;

Ч^ Ч2»Чд ” величина усечения разрядной сетки соответственно на входе

ПРФ, на входе и выходе второго сумматора звеньев;

Qk - весовые коэффициенты согласно выражению (1);

Nk - размер к - окна суммирования по координате п .

Задаваясь допустимыми значениями ст погрешности (или отношением сигнал - шум при известных статистических характеристиках обрабатываемых изображений), из выражений (8-12) можно определить допустимое усечение разрядной сетки в различных точках ПРФ. Распределение усечений разрядной сетки в структуре ПРФ следует выполнять, исходя из требования наибольшей экономии аппаратных средств. При условии, что сумматоры, счетчики, регистры и схемы управления могут быть выполнены на основе технологии заказных и полузаказных СБИС, экономия аппаратных средств будет определяться, в основном, уменьшением числа БИС ОЗУ, необходимых для построения устройств задержки. Считая, что на каждый бит слова данных в элементах задержки приходится одна БИС ОЗУ, получим оценку сложности ПРФ:

V = 2ЬК + 2-Ь^К, где величины Ь и b - разрядность данных в элементах задержки 3, 4 и 5, 6

соответственно.

Рассмотрим в качестве примера ПРФ, предназначенный для восстановления изображений. Выберем из [3] модель наблюдения с импульсной характеристикой искажающей системы вида «Гаусс» и отношением дисперсий ошибки и изображения 0,01.

Реализации ПРФ с разным числом параллельных звеньев обеспечивают различные величины относительной ошибки восстановления. Выбрав в качестве точки отсчета погрешность восстановления с помощью КИХ-фильтра, реализуемого прямой сверткой, в окне размером 9x9 отсчетов, определим необходимую разрядность данных в ПРФ, не уступающих по точности КИХ-фильтру. Оценки погрешности, приведенные в [3], получены для неквантованного представления отсчетов изображения. Применение в ПРФ арифметических устройств с конечной длиной разрядной сетки вызовет дополнительные ошибки в выходном сигнале. При расчете погрешностей воспользуемся формулами (9), (10). Дисперсию ошибки, вносимую квантованием, будем оценивать по формуле где U - размах квантуемого сигнала;

В - число разрядов в слове данных.

Полагая, что входной сигнал имеет нормальный закон распределения, выразим размах сигнала через дисперсию изображения и получим из (14) выражение для относительной ошибки, вносимой квантованием:

.2 КВ 2

22В

И

В таблицу сведены рассчитанные с учетом выражений (9), (10) и (15) допустимые значения длины разрядной сетки на входе ПРФ. Величина относительной ошибки, вносимой квантованием, определялась как разность между оценками ошибки для КИХ-фильтра, реализуемого прямой сверткой в окне 9x9 отсчетов, и оценками ошибки для ПРФ, взятыми из [3]. Оценки сложности вычислены по формуле (13) с учетом того, что максимальный размер окна суммирования не превышает 15 х 15 отсчетов, и величина Ь1 должна быть, согласно выражению (6), больше, чем Ь, на 4.

Наименьшей сложностью обладает ПРФ с 5 рекурсивными звеньями, хотя теоретически достаточную точность обеспечивает ПРФ, имеющий 4 звена. Применение в ПРФ обычного для систем обработки изображений представления данных 8-разрядными словами позволяет считать погрешности, вызываемые квантованием, пренебрежимо малыми.

С целью проверки работоспособности ПРФ с разработанной структурой (см. схемы на рисунках 1, 3, 4) был изготовлен макетный образец фильтра. РекуР"

Параметры параллельно-рекурсивного фильтра для восстановления изображений

К а2 /а2 кв' и В V 4 0 00 00 5 0, 0014 6 160 6 0,0018 5 168 7 0,0019 5 196 8 0, 0020 5 224 9 0,0022 5 252 10 0,0022 5 280 сивное звено ПРФ при реализации на микросхемах средней степени интеграции занимает одну плату в стандарте КАМАК (около 70 микросхем). Испытания макета показали его работоспособность и высокую производительность.