Application of Cosmos's law of Merge and Split for Data Encryption

Published Online May 2017 in MECS

Sensitive data are always flowing amidst the huge bulk of data over the internet and are always prime target of intruders. These data can belong to government, defense department, business organizations, or to others. But initially data encryption was utilized in military services and in government procedures to ensure secret data communication. But now with time its area of application has become wider. Now it has expanded in many arenas. As a sample corporate arena is one of the application zones which deal with large amount of precious data on a daily basis. Therefore a robust protection mechanism is required for both moving as well as static data. Static data can be also called as data at rest, stored in storage devices as USB flash drives, hard disk. Conservation of valuable static data turns simple files into encrypted files. But information is still not secure as adversaries are always active and tries various ways to crack encrypted files. Some common type of cryptographic attacks are stolen cipher text attacks, attack on encryption keys, insider attacks, data corruption attacks or integrity attacks, data destruction attacks and ransomware attacks. To ensure security from these kinds of attacks data fragmentation and active defense data protection technologies are used. In this type of technologies cipher texts are distributed or moved or mutated. Hence it becomes tough for hackers to recognize, steal, and destroy data. Protecting only static data is not enough, movable data also need protection that means data in transit. Data flowing through massive networks also used to be intercepted. These kinds of interception have become too common. Hacking tools are being modernized day by day and as a result processors are becoming more powerful and fast. Hence an active step towards the encryption technique is required to take the challenge of shielding data from the pernicious attempts of adversaries. “Graph theory” is a very newly evolved sub-branch of discrete mathematics having a span of less than 300 years, but has proven to be one of the most superior tools for developing varied kinds of techniques in the field of networking and information security. In this context, the discussion begins with the intellectual property protection (IPP). Watermarking techniques can be exploited in intellectual property protection (IPP). This is done by evaluating watermarking techniques for the graph coloring problem [5, 7]. Ad-hoc networks are the basis of modern networking infrastructure. Their protection is one of the most challenging tasks, yet can be resolved with the aid of graph based tools as via selective encryption mechanism using a message specific key and spanning tree notion of graph theory. In selective encryption mechanism only selected data packets used to be encrypted [12]. Data encryption algorithm can also be emerged as a combination of notions. The data can be transformed to a structure that consists of numbers and letters by applying basic mathematical concepts like Venn-diagram and graph theory [6]. Graphs can be utilized for designing block ciphers, stream ciphers or public-key ciphers. Graph based Modified Data Encryption Standard (GMDES) algorithm is a graph automorphism oriented partial symmetric key algorithm which is not totally reliant on secret key and generates distinct cipher text by applying similar key on the similar plain text [2]. The proposed technique in this paper employs the dynamic node fusion property of graph theory. Here fusion is one of the properties of graph theory that states a pair of vertices x, y in a graph “G” can be called as fused that is merged or identified, if these two vertices can be substituted by a single new vertex so that, the edges that were incident on either x or y or both are still incident on the new merged vertex. So the fusion property as per the explanation given above is not associated with the modification in the number of the edges but is associated with the reduction in the number of vertices by one [15]. The proposed technique considers isolated vertices that used to form disconnected graph where each vertex possesses zero degree and hence after fusion also possess zero degree. It is a universal truth that static things are more recognizable than dynamic ones. Cryptography is a field where confidentiality rules. The importance of confidentiality activates the sense of using dynamic keys rather than static ones. The solid evidences which exist behind this notion are expressed in several recent research papers. The presented paper includes small collection of some of them. The very first among them states the essentiality of dynamic keys or one-time used symmetric cryptographic keys in improvising the security of cryptographic systems. As per the dynamic key theory, the dynamic keys play a vital role in enhancing the security of symmetric cryptography. A significant reduction in the probability of breaking the cryptographic system is observed which is:

2 ^s

to ms+s

.

Where “s” is the bit length of cryptographic key and “m” is the number of remembered parameters [4]. The second collection unit illustrates a symmetric key based security system in which dynamic key is generated from a multimedia file to encrypt any kind of multimedia data [10]. The third component of the collection elaborates a block cipher technique, which utilizes Linear Congruential Generator (LCG) for generating dynamic key that assists the implementation of the symmetric cryptographic system [13]. The last component of the collection elaborates about the Secure Data Storage Manager (SDSM) system that employs a dynamic approach to determine encryption key, which eliminates the single instance of encryption key [9]. Hence, brute force attacks performed with the assistance of even fastest processors can be restricted with the support of various kinds of dynamic keys generation techniques. The proffered technique can easily take the challenge of handling large length data along with the flexibility in terms of choosing encryption strength determination factor with least computational effort. The technique is also capable of reducing the network load on packet transmission. Technique proposed is the result of intense observation of the rule followed by the cosmos that emerges the conception of data hiding based on the merging of billions of particles forming one structure and then again followed by splitting to generate those constituent particles. And this phenomenon goes on with other sets of particles in a cyclic mode. The creative logic behind the presented technique makes it simpler to understand as well as to implement. The robustness of the presented algorithm makes it unique among other encryption techniques as even in the situation where multiple users send the same message at the same time using the same encryption strength determination factor the encrypted data for each users varies, thus making it difficult for the intruders to retrieve the actual data sent as even if the intruder gets access to the set of encrypted data of the same plain data he/she will not be able to determine the actual algorithm used to encrypt the data hence will fail to retrieve the actual data. At each layer of the dynamic layered encryption technique data used to be hidden in the dynamic number of nodes in the haphazard manner. The soul of the technique resides in the two basic procedures “merging” and “splitting”. The degree of flexibility that is exhibited by the proposed technique is competitively more than any other technique. This flexibility resides in terms of usage as well as implementation. In terms of usage means each time user is given a chance to decide the value of encryption strength determination factor, that is the extent to which ordered constituents of data are tightly packed in a node, however its value changes in each iteration as well as the as the components of the ordered constituents of data also changes. Flexibility in terms of implementation means with slight changes in the parameters and conditions of the algorithm we can make it to behave differently at different situation as per our needs. The adaptable property of the algorithm which makes it independent of the input size is the notable achievement which keeps it ahead of all the present available techniques of textual data encryption.

• II.    Comparison With Earlier Workings

• III.    Basic Terminologies

This section covers all necessary terminologies that are significant in clarifying the understanding of the proferred algorithm along with references whereever required.

• A.    Cryptography

Cryptography or Cryptology is related to the conception of examining and exercising the techniques that insures the reliable communication even in the existence of attackers. After deep investigation protocols are made to restrict the unauthorized people from reading preserved information. Cryptography is majorly applied for computer keyword, ecommerce, ATM cards etc.

• B.    Symmetric-key cryptography

Common key is shared between the sender and the receiver. The effectiveness of the technique solely depends upon the key and its length [14].

• C.    Asymmetric-key cryptography / Public-key cryptography

• D.    Intruders/ Adversaries/ Attackers/ hackers

The unauthorized persons who try to have an illegal access over the communication network to disrupt the communication or to steal the information.

• E.    Plain Text

The actual message is called as “plain text”, which is actually sent by the sender.

• F.    Cipher Text

After alteration the message is called as cipher text.

• G.    Encryption

It is the procedure of transformation of plain text to the cipher text.

• H.    Decryption

It is the procedure of transformation of cipher text to the plain text.

• I.    Key

It acts as determinant that ascertains the functional output of a cryptographic algorithm.

• J.    Cryptanalysis

It is the performed with the target to find the breaches that exists in the cryptographic system. It is actually integration of mathematics, curiosity, intuition, continuance, hardware and other systems capabilities. Often cryptanalysis is practiced by commercial or noncommercial sectors to reveal the hidden information of opponents. Some common kinds of cryptanalysis attacks are Known-plaintext analysis, Chosen-plaintext analysis/ differential analysis, Cipher text-only analysis, man-in-the-middle attacks, timing/ differential power analysis. To generate a secure and flexible cryptographic system a deep analysis of all aspects are necessary that takes care of maximum kind of possible attacks.

• K.    Node

Here Node can also be considered as isolated vertex in terms of graph theory, is the real world entity which is supposed to keep data inside it [15].

• L.    DivisionFactor / Encryption Strength determination Factor

It indicates the total number of characters of the textual data that will be present in each node.

• M.    SentMergeNode

It indicates the node which contains the data which is to be sent with respect to a particular iteration.

• N.    SentNodearray

It is an array which contains SentMergeNode as an array element where each successive array element that is SentMergeNode is obtained as a result of successive iterations.

• O.    ResidualMergeNode

It is the node which contains the combined data of all the nodes which are not intended to send in a particular iteration.

• P.    Parray

It is the array which contains “P” that is number of nodes available with respect to each iteration as its array element.

• Q.    Pnarray

It is the array which contains “Pn” that is number of nodes which is to be sent with respect to each iteration as its array element.

• R.    Sequencearray

It is the array which used to contain the sequence of “Pn” amount of nodes out of “P” amount of nodes with respect to a particular iteration.

• S.    DivisionFactorarray

It is the array which used to contain the DivisionFactor value with respect to particular iteration as its array element.

• T.    ReceivedMergeNode

It is the node which contains the combination of ordered nodes in the order as indicated by the Sequencearray of the current iteration or it is the combination of the array elements of the Receivedarray.

• U.    Receivedarray

It can represent either an arranged sequence of nodes at particular layer of dynamic layered encryption technique or it can represent the final arranged set of decrypted nodes.

• V.    InitialReceivedMergeNode

It is the node which contains the combination of ordered nodes in the order as indicated by the Sequencearray of the current iteration.

• W.    Split1array

It is the array which contains array elements which used to be distributed in the Receivedarray to fill it.

• IV.    Fundamental Steps Related to the Presented Technique

• A.    Finding total number of nodes (P)

On the basis of the length of the data (l) that is to be sent by the sender and the value of the DivisionFactor, the total no of nodes (P) is found.

Then, P =------ l ------+ rfactor where

DivisionFactor rfactor = 0, if (l % DivisionFactor == 0 ).

rfactor = 1 , if ( l % DivisionFactor == 1 ) .    (1)

• B.    Finding total number of nodes to be sent (Pn)

As per requirement, it can be implemented in different ways by imposing different conditions. That is in case when total number of nodes (P) is less than or equal to 10 then number of nodes to be sent (Pn) will be equal to the total number of nodes(P) or if it is greater than 10 and is less than or equal to 50 then total number of nodes to be sent (Pn) will be found by dividing the value of total number of nodes (P) by 2 or if it is greater than 50 and is less than or equal to 100 then total number of nodes to be sent (Pn) will be found by dividing the value of total number of nodes (P) by 4 or otherwise total number of nodes to be sent (Pn) will be found by dividing the value of total number of nodes (P) by 6. As described below in algorithmic form:

if ( P <  10 ) then

Pn = P

Else if ( P <  50 ) then

P Pn = — 2

Else if (( P ^ 50 ) & &  ( P <  100 )) then

Else

• C.    Selection of “Pn” amount of nodes from “P” amount of nodes

The Selection of “Pn” amount of nodes that is number of nodes to be sent from “P” amount of nodes that is total number nodes is done by following the steps mentioned below:

Step 1:   Create a set of odd numbers and a set of even numbers by considering the boundary limit as l.

Step 2:   Selection of elements from odd set of numbers and even set of numbers is done on the basis the dynamic factor (f), which is obtained by extracting the last digit of the current milliseconds value (milli), and then putting that value in the formula:

_{log10 e}milli _.

And then from that obtained value the 3rd digit after decimal is extracted.

Step 3:    [initialization] set i = 1

Step 4:   While i <  P

Step 5:    if ( f % 2 == 0 ) then

Step 6:   Select an element from the ordered index of the even set of numbers by maintaining the cyclic order, in case when there is no element at that particular index then any immediate next index is chosen which possess an element and store it in the array named actualarray.

Step 7:   Index value with respect to even set of numbers is incremented by 2.

Step 8:   End if

Step 9:    if ( f % 2! = 0 ) then

Step 10: Select an element from the ordered index of the odd set of numbers by maintaining the cyclic order, in case when there is no element at that particular index then any immediate next index is chosen which possess an element and store it in the array named actualarray.

Step 11: Index value with respect to odd set of numbers is incremented by 2.

Step 12: End if

Step 13: Value of milli is incremented by 0.1.

Step 14: The dynamic factor (f) is obtained by putting the value of milli in the formula:

_{log10 e}milli _.

And then from that obtained value the 3rd digit after decimal is extracted.

Step 15:  Set i = i + 1

Step 16:  End

Step 17:   if ( P ^ 31 ) then

Step 18: Select Pn amount of nodes on the basis of the Calculated Index Position of the actualarray.

Step 19: End if

Step 20:   if ( P <  31 ) then

Step 21: Select Pn amount of nodes on the basis of the very First Index Position of the actualarray.

Step 22: End if

• D.    Logic behind the Calculated Index Position

We have found the Calculated Index Position by considering 3 parameters; we have set the first parameter with value 20 by assuming that in any iteration of the algorithm the Pn will be less than or equal to 20, we have set the second parameter “store” as the last digit of the current millisecond value and the 3rd parameter is volatile in the sense that we have to find the maximum prime number (prime) which satisfies the condition:

20 + store + prime <  P .

On the basis of the value of the prime found from the previous step, the Calculated Index Position is found as:

Calculated Index Position = store + prime

• E.    Finding the sequence of Pn amount of nodes

For finding the actual sequence of Pn amount of nodes from P amount of nodes, we have generated random graphs by successively choosing some amount of nodes from Pn amount of nodes until all Pn amounts of nodes are chosen. It renders the sense that a kind of cycle is followed in which each time random graph is generated consisting of number of nodes (nodecount) such that:

nodecount x Pn .

where in each turn except the last one nodecount value is obviously similar.

Random graph is generated in a dynamic manner such that for each user among the group of users who are sending the same message at the same time using the same value of DivisionFactor/ Encryption Strength determination Factor, different random graphs will be generated.

As random graph generation depends upon the two factors: current value of the millisecond factor and which number of user is active in a particular session. These two factors make the proffered algorithm much more robust and dynamic in nature. As per the results observed a wide range of variations is found in the cipher text for same length of data, sent at same time using same DivisionFactor/ Encryption Strength determination Factor value.

Distribution of data among P nodes as per DivisionFactor value

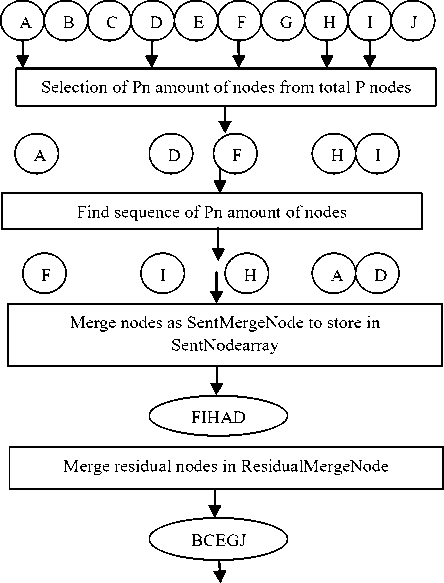
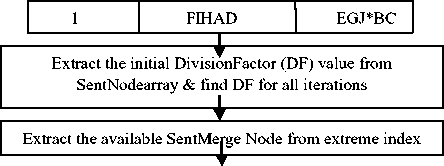
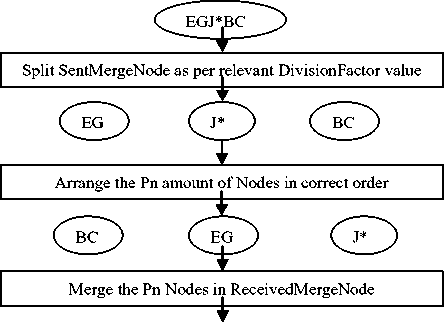
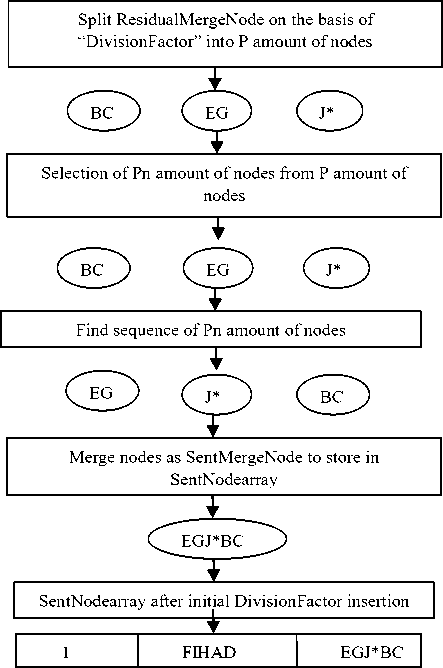
Fig.1. Diagrammatic Representation of Data Encryption

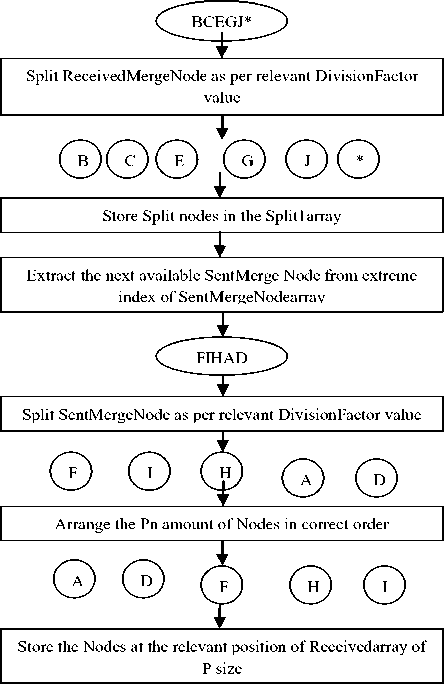
A

D

F

H

I

Distribute Split1array in vacant positions of Rec e ivedarray

A

B

C

D

E

F

G

H

I

J

Fig.2. Diagrammatic Representation of Data Decryption

• V.    Propoed Algorithms

The proposed technique is illustrated in terms of data encryption algorithm and data decryption algorithm as described below:

• A.    Encryption Algorithm

Steps mentioned below depict the proposed data encryption algorithm:

Step 1:   Take the data from the user and find the total length of the entered data and store it as “l”.

Step 2:   Take the “DivisionFactor” value from the user that is the total number of characters in each node

Step 3:    [initialization] set n = l

Step 4:   Repeat steps 5 to 12 while n is not equal to zero.

Step 5:   Find the total number of nodes (P) on the basis of “DivisionFactor” and “n”.

Step 6:   Distribute the (whole/ ResidualMergeNode)

data in the “P” number of nodes, last node may contain special characters (*) to maintain the uniformity of number of characters in each node.

Step 7:   Find the total number of nodes to be sent (Pn).

Step 8:   Find the “Pn” amount of nodes from “P”

amount of nodes and order of “Pn” number of nodes.

Step 9:   As per the found order of “Pn” number of nodes, arrange them and merge in a single node named as “SentMergeNode” and store it in the “SentNodearray”.

Step 10: Merge the residual nodes in a single node named as “ResidualMergeNode”.

Step 11: Decrement the value of” n” on the basis of “Pn”.

Step 12:  Increment the “DivisionFactor” by 1.

Step 13:  End

Step 14: Add the “DivisionFactor” value entered by the user as the key in the”SentNodearray”.

Step 15: Send the “SentNodearray” as encrypted data.

• B.    Decryption Algorithm

Step 1:   From the encrypted data received through

“SentNodearray” find the total length of the data as “l” by ignoring special characters (*) if any.

Step 2:   Extract the key that is the initial

“DivisionFactor” value that is totaling number of characters in each node as primarily set by user from the “SentNodearray”.

Step 3:   Set iterationcounter = 0

Step 4:    initialization set n = l

Step 5:   Repeat the steps from 6 to 14 while n is not equal to zero

Step 6:   Find the total number of nodes (P) on the basis of “DivisionFactor” and “n”.

Step 7:	Store the value of “P” in the “Parray”.
Step 8:	Find the total number of nodes to be sent (Pn).
Step 9:	Store the value of “Pn” in the “Pnarray”.
Step 10:	Find the “Pn” amount of nodes from “P” amount of nodes and order of “Pn” number of nodes and store them in the “Sequencearray”.
Step 11:	Store      the      “DivisionFactor”      in “DivisionFactorarray”.
Step 12:	Increment the “iterationcounter” value by 1.
Step 13:	Decrement the value of” n” on the basis of “Pn”.
Step 14:	Increment the “DivisionFactor” by 1.
Step 15:	End.
Step 16:	Set flag = 0
Step 17:	[initialization] set it = iterationcounter
Step 18:	Repeat steps 19 to 43 while it >  1
Step 19:	if ( flag == 0 ) then
Step 20:	Extract the itth “SentMergeNode” from the “SentNodearray”.
Step 21:	Split the “SentMergeNode” according to the itth value of the “DivisionFactorarray” into “Pn” amount of nodes as indicated by the itth value of the “Pnarray”.
Step 22:	Arrange the disordered nodes through the sequence represented by the itth “Sequence array”.
Step 23:	Merge the ordered nodes found from the previous step into a single node named as “ReceivedMergeNode” and copy it to the “InitialReceivedMergeNode”.
Step 24:	Split the “InitialReceivedMergeNode” array on the basis of (it-1)th value of the “DivisionFactorarray” and store it in the “Split1array”.
Step 25:	End if
Step 26:	if ( it - 1 ) th level is zero then
Step 27:	If “Receivedarray” exists then
Step 28:	Merge the “Receivedarray” in to a single node named as “ReceivedMergeNode” and it is the decrypted data hence break the process.
Step 29:	End if
Step 30:	If “Receivedarray” does not exists then
Step 31:	Send the “ReceivedMergeNode” and it is the decrypted data hence break the process.
Step 32:	End if
Step 33:	End if
Step 34:	if flag = 1 then
Step 35:	Merge the “Receivedarray” into a single node named as “ReceivedMergeNode”.
Step 36:	Split the “ReceivedMergeNode” on the basis of (it-1)th value of the “DivisionFactorarray” and store it in the “Split1array”.
Step 37:	End if
Step 38:	Extract the (it-1)th “SentMergeNode” from the “SentNodearray”.
Step 39:	Split the “SentMergeNode” according to the (it-1)th value of the “DivisionFactorarray” into “Pn” amount of nodes as indicated by the (it-

1)th value of the “Pnarray”.

Step 40: Arrange the disordered nodes through the sequence represented by the   (it-1)th

“Sequencearray”.

Step 41: Store the “Pn” nodes obtained from the previous step in the same order at the location represented by them in the “Receivedarray” of size “P” of the (it-1)thlevel.

Step 42: Distribute the “Split1array” at the vacant positions of “Receivedarray” and set flag = 1.

Step 43:  Decrement “it” by 1

Step 44:  End

• VI.    Complexity Analysis of the Algorithm

The execution time of the proffered algorithm does not depend upon the input size, hence possesses a constant execution time. To examine this fact two situations are analyzed and concerned algorithmic steps are revealed below in data driven mode. In the first case it is supposed that user enters data of length 100 characters long and gives DivisionFactor value as 5. Processing of the assigned values in the encryption algorithm takes two rounds to convert the entire pain text into the cipher text in which in the first iteration out of 20 packets 10 are sent and in the second iteration out of 9 packets all 9 packets are sent. In the second case it is supposed that user enters data of length 60 characters long and gives DivisionFactor value as 5. Processing of the assigned values in the encryption algorithm takes two rounds to convert the entire pain text into the cipher text in which in the first iteration out of 12 packets 6 are sent and in the second iteration out of 5 packets all 5 packets are sent. The signature algorithmic steps are expressed below in the data driven mode as:

Initially, DivisionFactor = 5

if P <  10 then Pn = P .

P if P ^ 10 then Pn = — .

• Case 1:

Length of data ( l ) = 100

Then from (1)

P = 20 And Pn = 10.

Current value of l = 50

Current value of DivisionFactor = 6

Then from (1)

P = 9 And Pn = 9.

Current value of l = 0

Total number of iterations = 2

• Case 2:

Length of data ( l ) = 60

Then from (1)

P = 12 And Pn = 6.

Current value of DivisionFactor = 6

Then from (1)

P = 5 And Pn = 5 .

Current value of l = 0

Total number of iterations = 2

It is clear that whether the length of the data is 100 or 60, the total number of iterations is 2. This renders the sense that the algorithm has no dependency on the input size. So, the algorithm has achieved a complexity of O(1).

• VII.    Expermiental Results of Presented Algorithm

The experimental result of the proffered algorithm is examined using Intel ® Core™ i3 processor. Here the supported system is a 64 bit machine with 6GB RAM capability. The programming language which is selected for implementing the algorithm is “C++” and the compiler used for this purpose is Dev-C++ compiler. The conditions which are imposed for implementing the proposed algorithm are as:

if ( P <  10 ) then Or if ( P <  2 ) then

Pn = P

Else if ( P <  50 ) then

P

Pn = —

Else if ( P ^ 50 & &  P <  100 ) then

P Pn = —

Else

P

Pn = —

The experimental results are presented below in the both graphical and tabular form to make the understanding of the execution of the algorithm clearer for different parameter values and different implementation conditions.

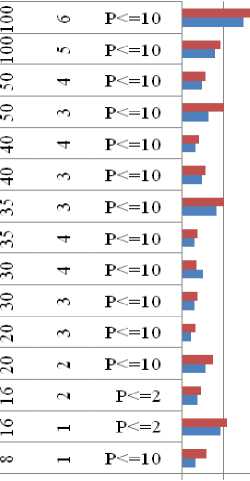
Here the first column represents the actual length of the data entered in terms of number of characters, the second column represents the DivisionFactor (DF) value, the third column represents the chosen condition for implementation and the fourth and fifth column represents the encryption and decryption time in seconds respectively.

Table 1. Encryption and Decryption Time for Chosen Data Length and Condition for Implementation

Length (l)	DF value	Chosen Condition (CC)	Encryption time(Sec)	Decryption time(Sec)
8	1	(P<=10)	0.626	1.164
16	1	(P<=2)	1.838	2.132
16	2	(P<=2)	0.734	0.886
20	2	(P<=10)	1.101	1.483
20	3	(P<=10)	0.439	0.632
30	3	(P<=10)	0.579	0.717
30	4	(P<=10)	1.025	0.687
35	4	(P<=10)	0.601	0.717
35	3	(P<=10)	1.616	1.983
40	3	(P<=10)	0.938	1.079
40	4	(P<=10)	0.638	0.784
50	3	(P<=10)	1.281	1.984
50	4	(P<=10)	0.93	1.086
100	5	(P<=10)	1.604	1.834
100	6	(P<=10)	2.97	3.285

1 D С 0    2   4

F С

■ I) ecryption Time

Encryption

Time

Fig.3. Graphical Representation of Tabular Data Showing Variations in Encryption and Decryption Time with Change in Value of Parameters

• VIII.    Conclusion

Data encryption algorithms are the center of attraction for those who are really concerned about their data. To them data means the resource that generates information that can help them to make further decisions in the path of their progression and if leaked can give a chance to their rivals to take disastrous steps against them. The huge demand of robust data encryption algorithm can only be fulfilled if a dynamic algorithm is designed which possesses less space complexity and time complexity, which is flexible and easy in terms of implementation, where it is not easy to determine the technique used behind the generation of cipher text even in the worst situations. Keeping all these requisitions in mind, the proffered algorithm is developed. The presented algorithm works in a dynamic manner. Each time user is given a chance to determine the initial Encryption Strength determination Factor / DivisionFactor that is initially how many characters will be present in each node, following this step nodes are dynamically selected, merged, sent and residuals are merged if present, the cycle goes on, till all nodes are not sent, with another set of nodes that are generated after diffusion of ResidualMergeNode. The proposed algorithm can be implemented in different ways if certain conditions are changed as condition set on the number of nodes to be sent in any iteration and number of nodes that will be selected for the random graph generation for determining the actual sequence of nodes to be sent. The presented algorithm is independent of the input size, due to its dynamic nature data are stored temporarily, hence possesses least space complexity as well as least time complexity which is O(1). The algorithm is highly resistible, even in the worst case situation when multiple users send the same message at the same time using the same DivisionFactor value then too it will be able to generate unique ciphers for each user.