Application of the Chaotic Ergodicity of Standard Map in Image Encryption and Watermarking

Published Online November 2010 in MECS

The fascinating development in digital image processing and network communications during the past decades makes digital image information used extensively. It has created a great demand for real-time secure transmission over the Internet and through wireless network. The security issue of digital images has attracted more attentions consequently. To meet the demand of real-time secure image transmission, a variety of encryption algorithms (for example, see [1-10] and the references therein) have been studied and developed. Among them, chaos-based encryption algorithms have been considered to be a significant technique in application thanks to the good properties of chaotic systems in many concerned aspects regarding security, complexity, speed, computing power and computational overhead, etc. As a matter of fact, due to some intrinsic features of digital images, such as bulk data capacity and high correlation among adjacent pixels, traditional encryption algorithms such as DES, IDEA and RSA are not suitable for practical digital image encryption. The fundamental features of chaotic systems, such as ergodicity, pseudo-randomness and high sensitivity to initial conditions and control parameters, are close to confusion and diffusion in the cryptography [4,8-9].

As an approach of image encryption, digital image shuffling technology is a research emphasis all the time. It can be used directly in digital encryption, and can also be used as the preprocessing and post-processing to enhance the robustness of digital image hiding and digital image watermarking. So the research of digital image shuffling technology is a fundamental work and needs more concerns. The basic idea of the technology is changing the image pixel positions through matrix transforms or position permutation to achieve the visual effect of disorder. The idea can also be expanded to the color space and frequency domain. Many image shuffling schemes have been proposed in the literature, such as Arnold map, Baker map, Standard map, Fibonacci-Q transform, Conway game, automata cellular [4-5, 8-11]. In this paper, two novel image shuffling schemes are proposed according to orbits of the chaotic Standard map. Different from the conventional shuffling schemes based on the discretized Standard map, we disorder the pixel positions by the orbits of its continuous version. After setting the initial positions and the control parameters, one can get an orbit by iterating the Standard map. Thanks to the chaotic ergodicity, the orbit will generically fill the square [0, 2 π )² ; the points on the orbit have their corresponding order numbers which can be used to permute the pixel positions. The proposed schemes do have at least three advantages compared with the traditional ones. 1) The scheme owns longer transformation period; 2) it is simpler to implement and can be generalized to any images with different width and height; 3) the key spaces are larger since the initial conditions are considered to be the additional cipher keys compared with the traditional shuffling schemes with just considering the control parameters as keys. Therefore the proposed schemes in this paper will thereby strengthen the security.

Digital watermarking provides an effective approach for copyright protection and content authorization. Many watermarking schemes are proposed in recent years [1119]. The basic principle of watermarking is to embed a weak signal in the host data without altering it significantly. The watermark is imperceptible usually, but it can be detected or extracted by specific algorithm, even after some manipulations to the watermarked data. In contrast to encrypted data, watermarked data can still be used while remaining protected. It does not necessarily prevent the copying of digital data, but should rather identify the original data source, so that copyright violations can at least be detected. The hidden signal travels with the data, which thus remains “marked” and protected, until the intended receiver removes the watermark. There are two methods of performing digital image watermarking, one in spatial domain, and the other in frequency domain. Watermarking in the spatial domain is easy to implement by embedding a watermark in selected areas on the texture of the host image by changing the gray values of the selected pixels. The disadvantage of this kind of watermarking is that the inserted information may be easily detected using computer analysis and the watermark cannot effectively resist image processing attacks such as cropping, compression, noise, and filtering, etc.

In order to enhance the robustness against malicious attacks, a variety of improved watermarking schemes have been proposed recently, see for example, [20-24]. Regarding watermarking in the spatial domain, the common way is to perform preprocessing to the host image and/or the watermark by performing some shuffling schemes, which makes the watermark transparent and strongly robust [11, 25-26]. The shuffling process has two advantages. On one hand, it makes the watermark bits spread uniformly all over the host image. Therefore, it can resist the attacks such as cropping, noise, compression, tampering effectively. On the other hand, it can also enhance the security of watermarking schemes by setting the cipher keys. Only the authorized consumers know the secret keys to restore the watermark and the original host image, while the non-authorized consumers fails even if knowing the watermarking scheme since they do not have the cipher keys. In this paper, a watermarking scheme with the preprocessing of host image by the proposed shuffling schemes is presented. The extracted watermarks shown that the proposed watermarking scheme is robust against attacks.

The rest of the paper is arranged as follows. Section II reviews the Standard map. Section III describes the details of the orbit based shuffling and encryption schemes proposed in this paper. A watermarking scheme using the proposed shuffling schemes as preprocessing is presented in Section IV. Attacking tests are presented in Section V. Some concluding remarks are outlined in Section VI.

• II.    S TANDARD MAP

The classical Standard map is described with the following mathematical formula [4]:

x n + 1 = ⁽ x n ⁺ У п ) mod² ^ ,

.Уп+1 = (Уп + c sin(xn + Уп )) mod2n, where c is a positive constant. The Standard map is commonly used in the design of almost all block symmetric ciphers. It can be discretized in a straightforward way by substituting x = i2n / N , y = j2n / N , c = C2n / N into (1). The discretized version of the Standard map is as follows:

5 1 = ( i + j ) mod N ,

SN

5 ₂ = ( j + C sin ——) mod N , 2 n

where C is a positive constant, and N is the height or width of the square image processed. ( i , j ) and ( S ₁ , S ₂ ) are the pixel coordinates of the original image and the shuffled image respectively. The conventional shuffling scheme based on Standard map changes the original image pixel at ( i , j ) to the shuffled image pixel at ( S ₁ , S ₂ ) . The Lena image and the shuffled image by applying the discretized Standard map one round with C = 3000 are shown in Figs. 1(a)-(b).

(a) Lena image

(b) Shuffled image based on the discretized Standard map

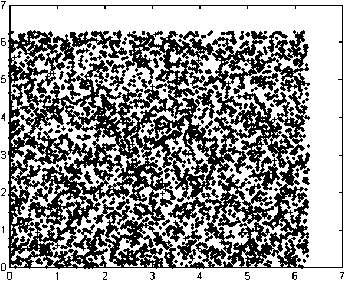
(c) The chaotic orbit ( X i , y i ) , i — 0, L , 6000

(d) Shuffled image based on shuffling scheme I Figure 1. The Standard map’s shuffling

• III.    A PPLICATION OF S TANADRAD MAP IN IMAGE ENCRYPTION

• A. Shuffling based on orbit ergodicity of Standard map

In this subsection, we propose a novel approach to shuffle digital images. It is well known that the Standard map (1) is chaotic in the square[0,2n) x [0,2n). The ergodic property of the chaotic map means that for most of the initial values (x0 , y0) , one can get chaotic orbits filling the square, which implies that a sufficient long orbit will almost fill the square. For any discrete pixel position (i, j) e[0, N -1] x [0, N -1] , there exists (Xk, Ук ) e [0,2n) x [0,2n) approximating (i2n / N, j2n / N). This ergodic property can be used to get an order number for every point (i2n / N, j2n / N) , i, j — 0,L , N - 1 . The obtained order number for pixel (i, j) , namely k , can be applied to change the pixel position (i, j) to the new position ([k/N] , mod(k, N)) , where [x] refers to the largest integer not larger than X and mod(к, N) is к — N *[к / N ]. If the same procedure is employed to all the pixels, one will get a shuffled digital image at last. The shuffled image owns a better shuffling result than that by conventional Standard map shuffling method. Another advantage for this kind of schemes is that it owns more secret keys, that is the initial position (x0 , y0) . From the security point of view, the proposed scheme in this paper is superior. Suppose that the original image is A with size N x N and the shuffled image is B with the same size. The proposed shuffling scheme I is outlined as follows.

Shuffling scheme I:

Step 1. Set the values of x ₀ , y ₀ and c .

Step 2. Iterate the Standard map (1) to get the orbit of (X0, У0) , say {(Xn, Уп ): n — 0,1,L , M} for a large number M ; discard the transitional part of the orbit {(Xn, yn ) : n — 0,L , T} to get an new orbit sequence {(Zn, Wn ) — (X„+t , Уп+t ): П = 1,L , M - T}•

Step 3. Decide the order number k for pixel position ( i , j ) by the first number k such that

Nz Nw

([ ^k ],[ ^k

2 n   2 n

]) — ( i , j ) •

Step 4. Let B ([ k / N ],mod( k , N )) = A ( i , j ) .

We note that one can get the order numbers for all the pixel positions theoretically as long as the orbit is long enough. In practice, in order to save the computational time and the storage space, one can’t get the order numbers for all the pixel positions. If there are pixel positions not ergodic, they can be put in the remainder part in the shuffled image orderly. The experimental results are shown in Figs. 1 (c)-(d), where we set ( x ₀ , y ₀ ) = (1.3123, 0.9001), M =230000, c =3000 and apply the scheme with one round. We discard the transitional part of the orbit {( X n , y n ) : n — 0, L , T } to get a new orbit. In this paper , we choose T — 1000 for all the experiments. One can observe that the shuffling effect is pretty good compared with the encrypted image shuffled by the traditional scheme based on the dicretized Standard map (2) .

It is well known that a good encryption algorithm should be sensitive to the cipher keys. In order to test the sensitivity of the cipher keys, namely, x ₀ , y ₀ , c , some experiments are performed. In Fig. 2(a), we set x ₀ = 1.3123+1.0e-15; y ₀ =0.9001, M =230000, c =3000 and apply the scheme one cycle as well. The difference between Fig 1(d) and Fig. 2(a) is 99.32%. In Fig. 2(b), we set x ₀= 1.3123; y ₀ =0.9001+1.0e-15, M =230000, c =3000 and perform the scheme one round. There is a difference of 99.33% between Fig. 1(d) and Fig. 2(b). In

Fig. 2(c), we set x ₀= 1.31231; y ₀ =0.9001, M =230000, c =3000+1.0e-12 and perform the scheme one round. The difference between Fig. 1(a) and Fig. 2(c) is 99.26%. The obtained results imply that shuffling scheme I is sensitive to the initial value ( x ₀ , y ₀ ) as well as the parameter c . The proposed shuffling scheme I has a better disordering effect compared with the traditional shuffling scheme based on the discretized form (2). Furthermore, one can employ more iteration rounds and use different initial values of x ₀ , y ₀ , c in each round to strengthen both the shuffling effects and the security.

(c)

Fig. 2. Results based on shuffling scheme I

Shuffling degree is another index to evaluate shuffling schemes [11]. Assume that the size of digital image P is H x W . We first compute the gray difference between pixel ( i , j ) and its four neighboring pixels by

GD ( i , j ) = 1 L t P ( i , j ) — P ( i ', j ')] 2 ,

⁴ i ' , j'

where ( i ', j ') = {( i - 1, j ), ( i + 1, j\ ( i , j - 1), ( i , j + 1)}.

Calculate all GD ( i , j ) for the whole image except those pixels at four sides and take the mean

(a)

H - 1 W - 1

LL GD ( i , j )

E ( GD ) = i = 2 ^j = 2 -----------.

( H - 2) x ( W - 2)

Let E ( GD ), E ^' ( GD ) be the mean gray differences of the original image and the shuffled image respectively. The shuffling degree is defined as follows.

GDD = E •( GD ) - ^{E (} GD )          (3)

E '( GD ) + E ( GD )

The value of GDD lies in [-1,1]. We note that if GDD is more near 1, the better shuffling effect is obtained. The conventional shuffling scheme (2) and the proposed shuffli ng scheme I are compared at the same iteration round.

The shuffling degree calculated by Fig. 1(a) and Fig. 1(b) is 0.3872. The shuffling degree yielded by Fig. 1(d) and Fig. 1(a) is 0.4388. The other three shuffling degrees calculated by Fig. 2(a) and Fig. 1(a), Fig. 2(b) and Fig. 1(a), Fig. 2(c) and Fig. 1(a) are 0.4392, 0.4405 and 0.4402, respectively. From the results, one can conclude that the proposed scheme is superior in shuffling effect.

B. Shuffling based on sorting of the orbit of Standard map

In this subsection, we propose another approach to shuffle digital images. Thanks to the chaotic nature of the Standard map in the square [0, 2.П )² , one can easily get one chaotic orbit {( X_n , y_n ): n = 1, L , H x W } for most of the initial values ( x ₀ , y ₀ ) with given control parameter c . We rearrange all the x_n ( y_n ) values of the orbit to get one new sequence { x n ( y_n ): n = 1, L , Hx W } according to the order from small to large. As a result, we also get an index order number for every x_n ( y_n ) in the new sequence. The index order number sequence can be applied to permute the image pixel positions and therefore scramble the image to get a encrypted image. The shuffling scheme II is outlined as follows.

Shuffling scheme II:

Step 1. Set the values x ₀ , y ₀ and c .

Step 2. Iterate the Standard map (1) to get the orbit of ( X 0 , У 0 ) , say {( X n , У п ): n = 0,1, L , H X W } where H , W are the sizes of the considered image.

Step 3. Rearrange { X n : n = 1, L , H X W } to get an index order sequence { Ix n : n = 1, L , H X W } ; the same process is applied to { y n : n = 1, L , H X W } to get the corresponding index order sequence { Iy n : n = 1, L , H x W } .

Step 4. Reshape the gray scale values of the digital image A sized H X W to one vector V with length H X W ; permute the vector V by { Ix n } first and then by { Iy_n } to get one new vector V ₁ .

Step 5. Reshape V ₁ back to one 2D matrix and we can get the shuffled image B .

The reconstruction process is just the inverse and it is easy to implement. The experimental results are shown in Fig. 3. In Fig. 3(a), we set ( x ₀ , y ₀ ) = (2.3123, 0.3201), k = 2000 and apply shuffling scheme II just one round. One can observe that the shuffling effect is also better than Fig. 1(b).

(a)

(b)

(c)

(d)

Figure 3. Results based on shuffling scheme II

The sensitivity of the cipher keys for shuffling scheme II is also simulated. In Fig. 3(b), we make a small change at x ₀ with a perturbation 1.0e-15 and set the other initial conditions unchanged. The difference between Fig. 3(b) and Fig. 3(a) is 99.29%. In Fig. 3(c), we just replace y ₀ by 0.3201+1.0e-15 and perform the scheme one time as well. There is a difference of 99.29% between Fig. 3(c) and Fig. 3(a). In Fig. 3(d), the only changed value is c with a difference 1.0e-12. The difference between Fig 3(d) and Fig. 3(a) is 99.44%. The experimental results imply that shuffling scheme II is very sensitive to the initial values x ₀ , y ₀ and the control parameter c . The proposed shuffling scheme II has a better disordering effect compared with the traditional schemes. Furthermore, one can employ more iteration rounds and use different initial values x ₀ , y ₀ , c in each round to enhance both the shuffling effect and the security.

• C. A novel image encryption scheme and its security analysis

The two shuffling schemes presented in Subsection A and Subsection B are employed to form an image encryption scheme with a small revision to shuffling scheme II. We use the chaotic sequence

{ y „ : n = 1, L , H x W } to make a pseudo-random image R with the same size and gray scale level as those of the plain image Lena. The gray value matrix R is then XOR-ed with the shuffled image to change the pixel gray values of the whole shuffled image, which makes the histogram of the resulted cipher image B different from that of the plain image Lena A . The encryption scheme is proposed as follows.

Encryption scheme:

Step 1. Apply shuffling scheme I to scramble the plain image A to get a shuffled image B ₁ .

Step 2. Set the values x ₀ , y ₀ and c . Iterate the Standard map (1) to get the orbit of ( x ₀ , y ₀ ) , say {( X_n , y_n ): n = 0,1, L , H x W } where H , W are the sizes of the considered image.

Step 3. Rearrange { X_n : n = 1, L , H x W } to get an index order sequence { Ix_n : n = 1, L , H x W } ; quantize { y_n : n = 1, L , Hx W } with mod([ q x y_n ],256) to get a pseudo-random vector and then reshape the vector to be a gray scale image R with the same size and gray scale level as those of the plain image Lena. In the experiments, we set the quantization parameter q =1000.

Step 4. Reshape the gray scale values of the shuffled image B ₁ yielded by Step 1 to one vector V with length H x W ; permute the vector V by { Ix_n } to get one new vector V ₁ .

Step 5. Reshape V ₁ back to one 2D matrix and we can get a shuffled image B ₂ . B ₂ is then XOR-ed with the pseudo-random gray-scale image R to get the encrypted image B .

As mentioned in Subsection A and B, the two shuffling schemes are very sensitive to the initial conditions and the control parameters. In the encryption scheme, the same conclusion is also satisfied although we modify shuffling scheme II with XOR-ing operation to change the histogram of the processed image. It is also known that a good cryptosystem requires the key space sufficiently large to make brute-force attack infeasible. In the propose encryption scheme in this paper, the key space is at least (10 16 x10¹⁶ x10¹⁶)² = 10 96 derived from the initial conditions x ₀ , y ₀ and the control parameter c without considering the value T used in shuffling scheme I and the quantization parameter q . If we perform the encryption scheme with more rounds, it will be more secure to resist brute-force attacks. The experimental results are shown in Fig. 4. The parameters are the same as those in Fig. 1(d) and Fig. 3(a).

Figure 4. The encrypted image

Shannon pointed out in his masterpiece [27] that it is possible to solve many kinds of ciphers by statistical analysis. Therefore, passing the statistical analysis on cipher image is of crucial importance for a cryptosystem. Indeed, an ideal cipher should be robust against any statistical attack. In order to prove the security of the proposed encryption scheme, the following statistical tests are performed.

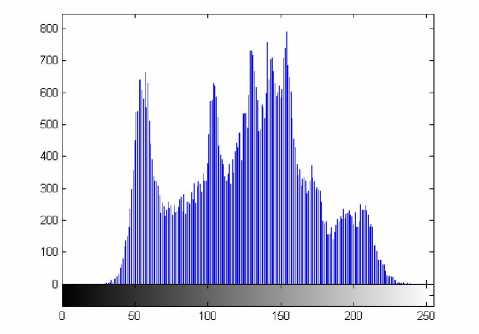
• (i)    Histogram: Encrypt the test image Lena with one round, and then plot the histograms of the plain-image and cipher-image as shown in Figs. 5(a)- (b), respectively. The latter figure shows that the histogram of the cipherimage is fairly uniform and significantly different from the histogram of the original image Lena and hence it does not provide any clue to employ any statistical analysis attack on the encrypted image.

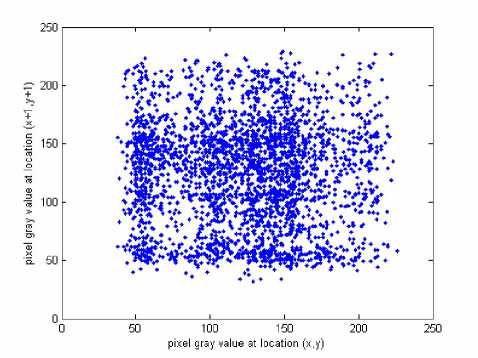
• (ii)    Correlation of adjacent pixels: To test the correlation between two adjacent pixels, the following performances are carried out. First, we select 3000 pairs of two horizontally adjacent pixels randomly from an image and then calculate the correlation coefficient r_xy using the following formula:

cov( x , y )

rxy    D(x) D(y)

where

• 1    ^{N 0}

cov⁽ x , y ) = — ^ ⁽ x - E ^{( x ))(} y i - E ⁽ У )) , N о

1 ^{N 0}                   1 ^{N 0}

E ⁽ x ) =— ^ X , D ⁽ x ) =—E⁽ X ^- E ^{( x})) .

N 0 i = 1                N 0 i = 1

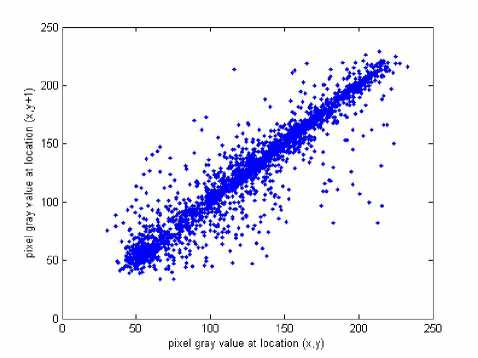
• x , y are the grey scale values of two adjacent pixels in the image and N ₀ =3000 is the total number of pixels randomly selected from the image. The same operations are performed along the vertical and the diagonal directions, respectively. Table 1 lists the correlation coefficients of the plain image Lena and its encrypted image, while their correlation distributions are depicted in

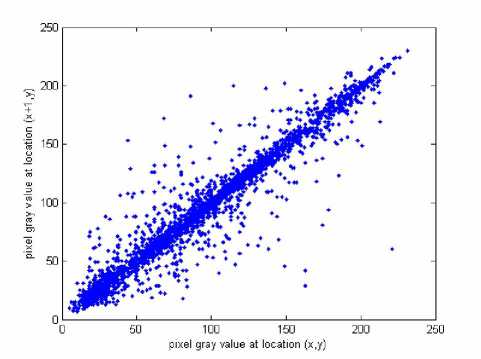
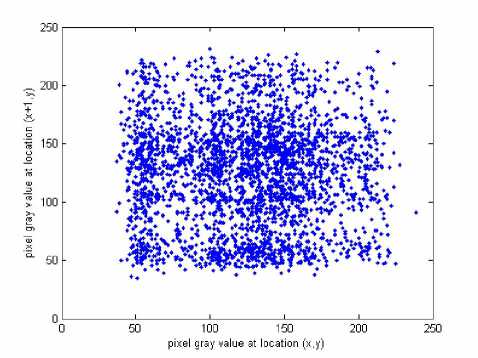
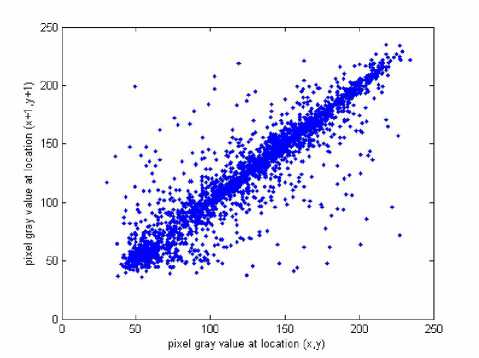
  Fig. 6. The correlation coefficients of the encrypted image are very small, implying that no detectable correlations exist between the original image and its corresponding encrypted image. Therefore, the proposed scheme owns high security against statistical attacks.

  
  
  
  

  (a) Horizontal direction of the plain image.

  
  
  

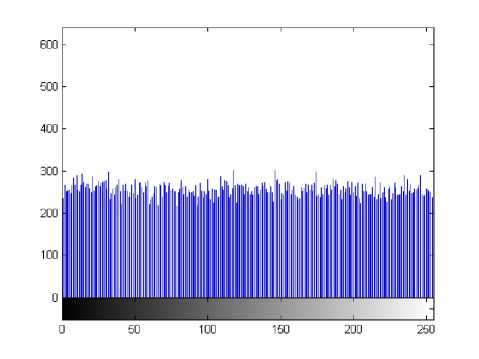
  Figure 5. The histograms of the plain image and the encrypted image

  
  
  

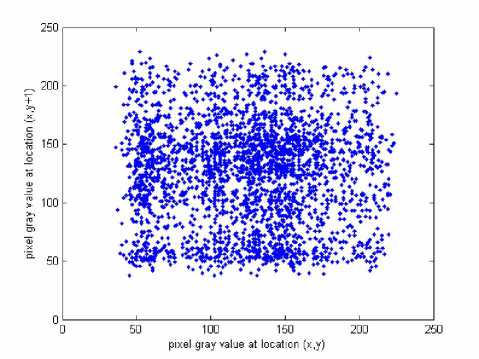
  (b) horizontal direction of the encrypted image.

  
  

  Table 1. Correlation coefficients of two adjacent pixels in the plain image and the encrypted image

  	plain image	shuffled image
  Horizontal	0.94630	0.00044
  Vertical	0.96349	-0.00129
  Diagonal	0.91788	-0.00646

  
  
  

  (c) Vertical direction of the plain image

  
  
  

  (d) Vertical direction of the encrypted image.

  
  

the entropy H ( m ) of a message source m can be measured by

L - 1

H ( m ) = - ^ p ⁽ m jlog p ⁽ m )

i = 0

where L is the total number of symbols m_t E m , p ( m ) represents the probability of occurrence of symbol m and log denotes the base 2 logarithm so that the entropy is expressed in bits. For a random source emitting 256 symbols, its entropy is H ( m ) = 8 bits. For the encrypted image of Lena, the corresponding entropy is 7.9973bits. This means that the cipher-image is close to a random source and the proposed algorithm is secure against the entropy attack.

(e) diagonal direction of the plain image.

• IV.    W ATERMARKING SCHEME

A watermarking scheme is proposed in this section. We first use the two shuffling schemes I and II proposed in Section III to scramble the host image and then imbed the watermark in the shuffled host image. The watermark image can be detected or extracted easily. The watermark embedding scheme is proposed as follows.

Step 1. Apply the shuffling scheme I to shuffle the original host image P sized m 1 x n 1 , we get a shuffled host image P ₁ ;

Step 2. Apply the shuffling scheme II to shuffle image P ₁ , we get a shuffled image P ₂ ;

(f) diagonal direction of the encrypted image.

Figure 6. Correlation distributions of two adjacent pixels in the plain image and the encrypted image.

Step 2. Assume the watermark image W with size m ₂ x n ₂ , which is usually smaller than the host image. We take the left-top part P ₃ of the shuffled image P ₂ with the same sizes as those of W :

P 3 = { P ₂ ( i , j ) 10 2 -1,0< j <  n 2 -1} .

The following formula is applied to imbed the watermark image into P ₃ :

P s = (1 - 1)W + tP 3 , t e (0,1) .

Step 3. Put P_s back to the left-top part of P ₂ and apply the inverse shuffling schemes to get an image imbedded watermark.

We also perform the information entropy analysis for the proposed encryption scheme. It is well known that

We note that t E (0,1) should be chosen suitably in the imbedding scheme. If t is too small, the quality of the watermarked image will be influenced. If t is too large, the information of the watermark image becomes weak and it is difficult to extract the watermark image. The extraction scheme is just the inverse of the imbedding scheme and is easy to work. Fig. 7 shows the image imbedded watermark with t =0.9, the watermark image and the extracted watermark image.

(a) Watermaked Lena image

(b) Cropping attack with cut-off 128X256 at the top half

/Ш^ /Ш^

(b) Original watermark (c) Extracted watermark

Figure 7. The watermarking results

• V.    ATTACKING TESTS

  In this section, experiments are performed to test the robustness of the proposed watermarking scheme. Attacks in the experiments are cropping, salt and pepper noising, Gaussian noising, and JPEG compression, etc. Experimental results show the proposed scheme is robust against the mentioned kinds of attacks. All the attacking tests are applied to the watermarked image with parameters ( x ₀ , y ₀ ) = (1.3123, 0.9001), M =230000, c =3000 in shuffling scheme I and ( x ₀ , y ₀ ) = (2.3123, 0.3201), c = 2000 in shuffling scheme II. The parameter t in the watermarking scheme is 0.9. The experimental results are shown in Fig. 8.

(d) JPEG compression attack with quality 60

(a) Cropping attack with cut-off 128X128 at the left-top corner

(e) Daubing attack

(f) Gaussian noising attack with mean 0 and variance 0.01.

(g) Speckle noising attack with mean 0 and variance 0.02

Figure 8. Results of attacking tests.

• VI.    CONCLUSION

In this paper, we apply the chaotic characteristics of the Standard map to image encryption and image watermarking. The proposed shuffling schemes are based on the continuous Standard map instead of the discretized one. As a result, the proposed schemes own more advantages, mainly including: 1) it is easy to implement without needing to discretize the map; 2) the key space is larger compared with the traditional ones. The proposed shuffling schemes are then employed in the pre-processing of watermarking scheme. Experimental results demonstrate that the host images embedded watermark are robust against various attacks and the scheme is simple to manipulate. Multi-watermark can be developed from our watermarking strategy as well because of the sizes of the watermark images are usually smaller compared with the host images. Several watermark images can be placed in non-overlapping regions of the shuffled host images. We will explore the algorithm on other transforms in the future work.

A CKNOWLEDGMENT

This research was supported by National Natural Science Foundation of China (No. 11071152) and Natural

Science Foundation of Guangdong Province (No. 10151503101000023).