Application of the entropy theory for electric connection schemes reliability analysis of traction substations

The main consumer of the electric power on railway transport is the alternating current electric train (ACET). Therefore, the functions of the traction substation (TS) are transformation of the electric power from one voltage level to another and power distribution through contact network by means of a feed line, with its subsequent transfer on the ACET current collector. Besides this ACET, traction substations implement the electric power supply of railway stations, locomotive and carriage depots, communication devices and automatic lock-outs, adjacent houses and the industrial enterprises. The violation of power supply and distribution, in turn, involves violation of the schedule and idle time of trains, shutdowns of the adjacent enterprises operation and the electric power supply of non-traction consumers, etc [1].

The comparative analysis and abilities assessment of the existing methods shows the necessity to develop the method of TS’s functioning reliability and effectiveness analysis as a complex technical system with a large number of states, basing on traditional methods, considering on features of construction and functioning of this system.

The purpose of the issue is the development of the method based on entropy assessment and its application reliability assessment of electrical connections traction substations of 110–220 kV schemes.

The following tasks are solved in the present article:

• •    the research of entropy estimates using possibility for the analysis of TP reliability;

• •    the calculation of entropy indicators of reliability for various TP 110–220 kV schemes;

• •    scheduling the reconstruction of TP 110–220 kV schemes.

Application of an entropy theory for the electric installations reliability analysis

The sets variety degree of any elements (events, states) depends on total number of the elements entering this set and their specific gravity in this set. Specific weights of various elements usually are defined by the probability to receive an element of this type at random sampling of this set.

There is the entropy of this set A elements determined by expression [2] serves in cybernetics for the variety measurement of a set:

n

H ( A ) =- g p i log p i ,                                           (1)

where H(A) – the entropy of the set A ; p _i – emergence probability of an element i at random sampling

n of a set of A. Toting is made with all elements of the complete set of elements ^pi = 1.

i = 1

The entropy defined on (1) has the following properties:

• •    the entropy reaches in zero when emergence of one element of a set is reliable, and others is impossible;

• •    at the given number of various elements the entropy has a maximum when emergence of these elements has the same probability;

• •    the entropy increases at increasing in number of elements in a set;

• •    the entropy has property of additivity: when sets of independent elements (events) unite in one, their entropy is summarized, and the sum is an entropy of the integrated set.

The entropy can be used as reliability assessment of a system by definition of indeterminacy measuring of system conditions in the quantitative look through its probabilistic characteristics [3].

Entropies for the difficult sets (for the difficult sets of their entropy) are calculated by means of tables of a higher transcendental function n( p ) = - p log 2 p .

Under union of two sets A and B with possible elements, a 1 ,…, a n and b 1 ,…, b m is understood a set ( A , B ) which elements represent all possible combinations of the a_i and b_j elements which number is equal to n·m .

Designating through p_ij the emergence probability of the a_ib_j element in a set ( A , B ).

The definition (1) represents an entropy of a set ( A , B ):

nm

^HU,B) =^-^ й p j ^log2 p j .

The united entropy is equal to the sum of items’ entropies at uniting of independent events sets (elements, actions):

^H ( A , в ) = H ( A ) + H ( B ).                                              (2)

We receive the equation in case of uniting dependent sets:

H ( A , B ) = H ( A ) + H ( B I A ) = H ( B ) + H ( A / B ),                          (3)

here are H(A/B) , H(B/A) - average conditional entropies of sets А and В.

The conditional entropy of a set of B provided that in a set of A the a i , element appeared, is called the value determined by the equation:

H ( B / a i ) = j^n [ P ( b j I « i ) ] , y= 1

where P(b_j /a_i ) – the conditional probability of emergence of the b_j element a set of B if in a set A the a element appeared.

i

The average conditional entropy H(B/A) is defined as an expectation of the conditional entropy:

n н(вм) = ^ рН ( в / ai) = 1 or nm H(B/A) = ^ £ p , n( b j /af).                                           (4)

i = 1 j = 1

The inequality is called the main inequality of Shannon:

H(B/A) < H(B).                                                           (5)

From (5) and (3) follows that H(A, B) < H(A) +H(B), H(A,B,C) < H(A) +H(B) +H(C).

Thus, the entropy is a measure of the elements variety of any sets. If these elements are casual events or conditions of any physical or technical system, then the entropy is a measure of indeterminacy – 316 – of a condition of this system. As shown in [4], the entropy can become also a measure of unreliability of a system under some conditions.

If the task of all system entropy determination in general is set, the information measuring for a set of elements n (everyone from which has two states) can be determined by expression:

H = - £ ( P i log 2 p_t + q jog 2 q i ) ,                                         (6)

i = 1

where p i – the probability of non-failure operation; q i – the probability of i -element failure of the system.

Expression (6) reflects existence of the general measure of information or the generalized entropy.

Stati tical data on behavior of a system are necessary to be used in this formula: the number of failures and restitutions, a response time in operating condition, in the condition of failure, etc.

Any power supply system or traction substation which is exposed various accidents and devices of relay protection and false drops of automatic relaying protection equipment (ARPE) can be presented by the following scheme (Fig. 1). D is a set of potential damages and accidents; L is a system of couplings and conditions in electric installation (EI); E is a set of conditions of EI; R is a set of possible actions of ARPE.

According to [5] the following condition is satisfied for the specified sets:

H ( E ) >  H ( D ) + H ( R / D ) - H ( R ),                                     (7)

where H(E) – the entropy of the conditions set of EI; H(R), H(D) – the entropies of sets of R and D ; H(R/D) – the average conditional entropy of sets of R at the influence determined by the managing director from a great number of D .

Inequality (7) is a formula of a law of requisite variety [5]. According to (7) entropy of conditions of H(E) has a minimum, and this minimum will be the least if R is the single-valued function from D , i.e. ARPE has fault-free operation:

H ( E ) = H ( D ) – H ( R ) when H ( R / D ) = 0.                                (8)

It is possible to claim that the minimum value of an entropy of states H(E) can be reduced concerning an entropy of indignations of H(D) only due to the same increase in an entropy of actions of ARPE. The entropy of a set of conditions of EI H(E) is defined both its normal operational, and the critical conditions and is a measure of indeterminacy of conditions of EI. Therefore, (8) is the expres-

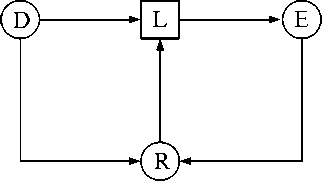
Fig. 1. Relations between sets of D, E and R sion for minimum unreliability which can be provided at the given set of accidents D and a set of the chosen influences R ARPE on condition of their non-failure operation.

The expression (7) allows to estimate a minimum of unreliability of the automated and operated EI taking into account a set of damages, a variety of the revolting influences of a variety of actions and reliability of its ARPE, because the entropy of H(R/D) is a measure of unreliability of actions of ARPE. Probabilities of element’s emergences of a set E can be connected with probabilities of EI elements finding in various states: normal (admissible) p_i and the emergency q_i . Then the entropy will be readiness measurement, measuring the indeterminacy to find EI in operational or non-operational state of its elements.

As the availability quotients of electric equipment are close to 1, the value of H q (E) is close to zero and its application is limited. Having determined probabilities of P and Q for all EI, it is possible to consider H q (E а ) as an uninterrupted operation measure.

The probabilities of elements’ appearance in set E can connected with probabilities of the failure events leading to non-operational conditions of Q(t) , and non-failure operation of P(t) during the given time of t . In this case the entropy H Q (E) will be non-failure operation measurement, measuring the indeterminacy to get non-failure operation or any EI’s failures.

The entropy H Q (E) is the function of time. H Q (E) is close to zero due to high probability of nonfailure operation by consideration of an infinitesimal interval of time. H Q (E) grows increasing the considered interval of time due to increasing in probabilities of failures and accidents and its maximum comes with a frequency of failures close to 1.

If in EI there are not any element’s failures leads to failure of all installation or to accident, then having connected entropy size only with two probabilities of P a and Q a = 1 – P a , where P a – the probability of fault-free operation, and Q _a – the probability of failure emergence, we will receive a failsafety measure H Q (E а ).

The probability of elements emergence of a set D can be connected with probabilities Q(t) of various elements failures in installation or probability of lack of any failures P(t).

The entropy of H Q (D) will be defined as an entropy or an indeterminacy measurement of damages and failures, and the entropy of indignations [6].

Entropies of readiness and uninterrupted operation of one element H_q(E_а) = H_q(E ) and

H q ( E ) = n( r ) + n( q ),                                                       (9)

where p is availability quotient; q – idle time coefficient, here p + q=1 .

The equation (10) is in case of one element for assessment of an entropy of non-failure operation H Q (E) and fail-safety of H Q (E а )

H q ( e ) = n( P ) + n( Q ),                                               (10)

where P ( t ) + Q ( t ) = 1, P ( t ) – the probability of non-failure operaion during t time; Q(t) – failure probability during t time.

In case of a Poisson stream of failures:

P(t) = e–a, where a – the average number of failures during t time; in case of the simplest stream a = λt.

There are various methods of assessment of reliability of power supply systems. However many of them were developed for a research of reliability of electric installations at design stages [4]. The analysis of the existing methods shows that assessment of system’s reliability of traction power supply under operating conditions and also in the course of reconstruction is expedient to use entropy criteria when scheduling versions of schemes of traction power supply.

Example. Schemes of systems of traction power supply of 110–220 kV are provided on Fig. 2.

The first scheme (Fig. 2a) is more prime and cheap. An alternative for this scheme is the scheme with application of more expensive, but also more reliable gas-insulated switches (Fig. 2b) instead of cheap one, but less reliable devices OD-KZ [7].

The scheme “Two Blocks with OD-KZ, and a Non-automatic Crossing Point from Lines” is forbidden by the modern norms of technological projection of PS [8] to application. However, it often meets on traction substations, and still is on stream for a delivery of contact network of the railroads. It is necessary to use alternating-current vacuum switches with the spring drive without oil isolation according to the requirements established by the owner of infrastructure [9], both on again constructed, and on the reconstructed linear devices of traction power supply.

Indicators of reliability of settlement elements of schemes are given in Table 1.

Estimating effectiveness of these actions by means of entropy indicators [4, 10]:

• •    H Q (E а ) is an entropy of fail-safety;

• •    H Q (D) is an entropy of indignations;

• •    H Q (R) is an entropy of actions of ARPE and a control system.

It is necessary to estimate those values to calculate presented indicators:

• a    – median number of repayments of consumers;

• Т t.av – average time of restitution of a delivery;

• q it – the value of coefficient of idle time.

For TS schemes (Fig. 2), calculated by a table and logical technique [4] at t_p = 1 year, the value of the specified indexes are provided in Table 2.

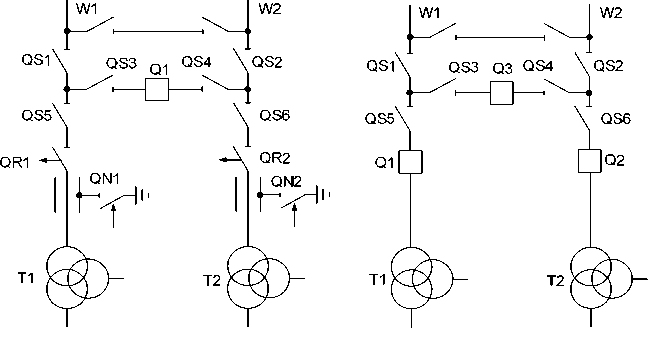
a )                                     b )

Fig. 2. a) scheme “Two Blocks with Separators and a Non-automatic Crossing Point from Lines”; b) scheme “Two Blocks with Switches and a Non-automatic Crossing Point from Lines”

Table 1. Indexes of reliability of the capital equipment of 110 kV [7].

Equipment	λ , 1/year	Тr, hours	Tpl, hours/year
The transformer, damage with short circuit (s.c.)	0,014	70	28
Disconnector, damage with s.c.	0,01	11	8
Separator, damage with s.c.	0,01	3,5	10
Short-circuit-maker, damage with s.c.	0,01	6	6
Gas-insulated switch 110 kV, damage with s.c.	0,2	30	25
Power line 35-220 kV	0,81	8,4	12

Note: λ – intensity of equipment failures; Т_r – restoring time; t _pl – delivery break time because of scheduled repairs.

Table 2. Indexes of reliability of traction substations (Fig. 2)

Scheme by the Fig. 2	λΣ	a, 1/year	Т t.av, hours	qab
a	0,8340	0,1325	1,21	0,18·10-4
b	0,2125	0,0229	5,32	0,14·10-4

The TS failure will be considered as the complete short and long periods of lost power. The reservation is carried out in case of refusal only one line of 110 kV. It means that the system will pass to a delivery from other line (reserved) in the absence of tension on a base line of a delivery, in the automatic mode.

For the scheme in Fig. 2 b we will consider calculations of entropy indicators in more details (index Q from H Q ( E ) and other indexes we will lower for record reduction).

From Table 2 for the scheme (Fig. 2b) of a = 0.0229, then by definition

H ( E a ) = ⁿ⁽ e - a ) + ⁿ⁽l - e - a ) = W⁷⁷⁴ ) + W226) = 0156

^H ( D ) = _§ H ( D ) =_§M e --) + ^[n(1 - e -" - )] = [ⁿ⁽ e -•■) + ^[n(1 - e -и +

+ [n( e + [n(1 - e -"“)] + [П( e   ) + [n(1 - e^-“1\ +

+ [n( e -•'=) + [n(1 - e -"-)] = 1 , 8602;

The entropy of actions of relay protection of a source

H (R) = n( Qsd) + п(1 - Qsd), где Qsd – the probability of a source shutdown

Qsd = ^Lqt, where q – the probability of finding element in a repair state during the year.

Qsd = 0,0041.

H ( R ) = n(0,0041) + n(1 - 0,0041) = 0,038 .

Table 3. Indexes schemes’ reliability

Scheme according to Fig. 2	H ( E a )	H ( D )	H ( R )
a	0,541	1,338	0,0398
b	0,156	1,8602	0,038

Entropy indicators were defined by using this technique. Results of similar calculations of these two schemes on the Fig. 2a are presented in Table 3.

Conclusions

It is possible to draw the following conclusions analyzing the results given in Table 3:

• 1.    The scheme in Fig. 2 b is the best by entropy estimates in terms of fail-safety. Entropy indicators are more sensing and allow to judge a condition of the traction power supply system, and its structural reliability.

• 2.    It is possible to estimate a share of presence of an entropy of a disabled state in total amount of the obtained information inherent in all structure of a system of traction power supply, comparing indicators. Such indicators are very useful as criterion at problem solving of reconstruction and modernization of traction substations. Thus, the entropy can be used as the size characterizing the level of structural reliability of a system of traction power supply.