Applying Quaternion Fourier Transforms for Enhancing Color Images

Published Online March 2012 in MECS DOI: 10.5815/ijigsp.2012.02.02

Fourier analysis is fundamentally a method for expressing a function as a sum of periodic components, and for inversely recovering the signal from those components. When both the function and its Fourier transform are replaced with discretized counterparts, it is called the discrete Fourier transform (DFT). Fourier transforms have been widely used in signal and image processing ever since the discovery of the Fast Fourier Transform (FFT) which made the computation of discrete Fourier transforms feasible using a computer [1]. It allows us to perform tasks which would be impossible to perform any other way; its efficiency allows us to perform other tasks more quickly. The Fourier transform provides, among other things, a powerful alternative to linear spatial filtering; it is more efficient to use the Fourier transform than a spatial filter for a large filter. As general, there are two main approaches to filtering an image. The first is the convolution of an image and kernel in the spatial domain. The second is the multiplication of an image's Fourier transform with a filter in the frequency domain. The fast Fourier transformation (FFT) algorithm, which is an example of the second approach, is used to obtain a frequency-filtered version of an image. Processing images by filtering in the frequency domain is a three-step process:

• 1.    Perform a forward fast Fourier transform to convert a spatial image to its complex Fourier transform image. The complex image shows the magnitude frequency components. It does not display phase information.

• 2.    Enhance selected frequency components of the image and attenuate other frequency components of the image by multiplying by a low-pass, high-pass, band-pass, or band-stop filter.

• 3.    p erform an inverse fast f ourier transform to reconvert the image from the frequency domain to the spatial domain.

According to the convolution theorem, filtering in the frequency domain can be performed by element wise multiplication of the Fourier transform by a suitable “Filter matrix”. The Fourier transform also allows us to isolate and process particular image “frequencies”, and so perform low-pass and high-pass filtering with a great degree of precision.

With the advances in the computing power and memory, color image processing has attracted much interest over the past few years. In this subject area, color image filtering is still an elusive challenge. Due to the multichannel nature of the color images, the key issue is how to couple the information contained in the given color ( e.g . red, green and blue) channels. Accordingly, conventional methods are used to separate a color image into three scalar images ( f_r(x,y),f_g (x,y) and f_h(x,y) ) and compute the two dimensional fast Fourier transforms of these images separately ( F_r(u,v"), F_g(u,v) and F₆(u,v) ) . Once these images are transformed into the frequency domain, filters can be applied to each image by convolutions. 2D FFT turns the complicated convolution operations into simple multiplications:

( F_r(u, v)H(u, v), F_g(u,v)H(u,v) and F_b(u,v)H(u,v) ).

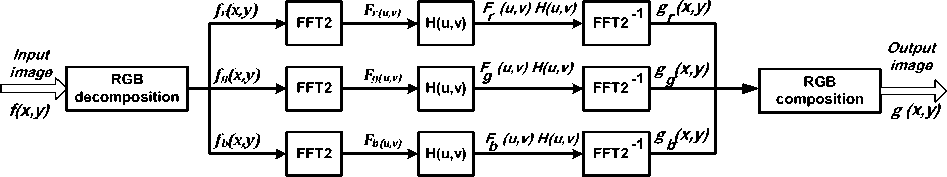
Fig.1 : filtering of color image in the frequency domain based on RGB decomposition

The inverse Fourier transform ( FFT2 - ) can then be computed for each channel yielding three output components ( g_T (x,y),g g (x,y) and g_b(x,y) ) . These components can be used to compose the filtered image g(x,y) (Fig.1). However, this approach fails to notice the inherent correlation between the components and results in color artifacts or blending. To avoid this, noise reduction process should be performed in a common and coherent way. The computing of the Hypercomplex 2D Fourier transform of a color image as a whole unit has only recently been realized. The quaternions have been proposed to be used to model color images [2,3], and it has been successfully applied in digital image processing [4-6]. Quaternions provide a new way to process color in combination. The advantage of the quaternion representation for color, as proposed by Sangwine [7,8], is that it combines a color 3-tuple (RGB) into a single hypercomplex number. A color can then be processed as a unit, rather than as three separate channels. Using quaternion operations, higher color information accuracy can be achieved because a color is treated as an entity. In this paper, the quaternion framework will be adopted for filtering color images since it offers scope to process color images holistically, rather than as separate color space components, and thereby handles the coupling between the color channels naturally. In this paper, firstly, a mathematical background concerning quaternions will be reviewed. This leads to the quaternion or complex representation of color image. The discrete quaternion Fourier transforms will be discussed as well. The second part of this paper address the problem of filtering color image in frequency domain using quaternion Fourier transforms. The Gaussian filter will be applied for color image filtering in the frequency domain. At last, evaluation results of typical filtering algorithms in MATLAB environment are summarized and presented.

• II.    BACKGROUND

A. Quaternions

The quaternions were discovered by Hamilton in 1843 [11]. They combine by the normal rules of algebra with the exception that multiplication is not commutative. A quaternion has four components, one real and three imaginary. The usual notation, extended from that of the complex numbers is:

q = w + xi + yj + zk(1)

where w, x, y and z are real, and i, j and k are complex operators which obey the following rules:

i2 = y2 = k2 = ijk  = -1

ij = k,   jk = i,   ki= j(3)

ji = -k,  kj = -i, ik= -j(4)

The pattern of signs in the products of different operators is easily remembered if the operators i,j and k are imagined on a clock face, arranged clockwise in alphabetical order. Multiplication of any pair of operators in a clockwise sequence produces a positive product, while multiplication in anti-clockwise sequence yields a negative product. The quaternion conjugate is:

q = w - xi-yj - zk                         (5)

And the modulus of a quaternion is given by:

|q| = 7w² + x² + y² + z²                           (6)

A quaternion with zero real part is called a pure quaternion, and a quaternion with unit modulus is called a unit quaternion. The imaginary part of a quaternion has three components and may be associated with a 3-space vector. For this reason, it is sometimes useful to consider the quaternion as composed of a vector part and a scalar part, thus: q = S(q) + V(q) , where the scalar part, S(q) , is the real part, and the vector part is a composite of the three imaginary components, V(q) = xi + yj + zk .

The product of two quaternion expressed in terms of their scalar and vector parts is given by:

qr = S(q) S(r) - V(q).V(r) + S(q)V(r) + S(r)V(q) + V(q)x V(r)                                          (7)

Where . and x operators denote the vector dot and cross products respectively. It follows from this that the dot and cross products of two pure quaternions, u and v are given by:

и x v = 2 (uv - vu)                             (8)

• 1 ,

и . v = - 2 (uv + vu)                              (9)

B.    Complex or quaternion representation of color images

It is possible to utilize hypercomplex numbers, in particular, quaternions, and to represent color image pixels as quaternions. Color image pixels have three components, and to model color images in quaternions, the real part is set to zero and the three color components are assigned to the imaginary parts. For example, a pixel at image coordinates (x,y) in an RGB image can be represented as:

f(x,y) = r(x,y)t + g⁽x,y)j + b⁽x,y)k (10)

Where r(x,y) is the red component and g(x,y) and b(x,y) are the green and blue components respectively. The image here is represented as a multivariate image of three vector components. So the resulting representation is a quaternion vectors of dimension the same as the number of pixels in the image.

f(x, y) = 7^ I'M 2 y=0 F r (u, v^M     (15)

Two-side IDQFT:

f(x,y) = Ж SSS y- ¹ e ^ ² "( ^XU)F L-R (u,v)e ^ ² "( ^Vy) (16)

• III.    filtering with quaternion fourier

TRANSFORMS

The process used to apply filters to an image is known as convolution, and may be applied in either the spatial or frequency domain. Within the frequency domain, convolution can be performed by multiplying the FFT (Fast Fourier Transform) of the image by the FFT of the kernel, and then transforming back into the spatial domain. For a digital image f ( x,y ) the basic filtering

Figure 2: Filtering of color image in frequency domain based on quaternion Fourier transforms

C.    Discrete quaternion Fourier transforms

Based on the concept of quaternion multiplication and exponential, the Quaternion Fourier Transform (QFT) has been introduced. Due to the non-commutative property of the quaternion, there are three different types of QFT defined: the left side QFT, the right side QFT and the two sides QFT. The earliest definition of QFT is the two-side form as following [9].

F q ⁽u,v) = f ” _m f ” _m e ^,uxf(x,y)e ^jVydxdy            (11)

And this equation can be generalized as:

F r (u,v) = ^ I^ l i y i f(x,y)e ^'X'     (12)

Two-side DQFT:

F l-r (u,v) = ^ I " _{ 1 l X 1 e '^l2,ri^

Similarly, the Inverse Discrete Quaternion Fourier Transforms (IDQFT) can be defined for the three types of QFT respectively as Left-side IDQFT:

f(x, y)= ^ I- i i y-1 е^И F_L (u, v)     (14)

Right-side IDQFT:

equation in the frequency domain is:

g ( x, y ) = 3^-1 { H ( U, V ) F ( U, V )} (17)

Where F ( u,v ) and H ( u,v ) are DFTs of the image and of the filter respectively. Their product is defined by array (element-by-element) multiplication. The quaternion convolution operation in the spatial domain corresponds to the product operation in the frequency domain [1014]. This is the same as the case of the conventional convolution. The basic model of filtering in the frequency domain is shown in Fig.2. Each RGB pixel of the input color image f(x,y) is transferred to a quaternion number, and then the 2D Fast Quaternion Fourier Transform (FQFT2) is applied to the image as whole unit yielding to F_q(u,v . The selected quaternion filter transfer function H_q(u, v) is then multiplied (element-by-element) by F_q(u, v). The filtered image g(x,y) can then be obtained simply by computing the inverse quaternion Fourier transform of the product F q (U,V)H q (U,V) .

To illustrate the practical application of quaternion Fourier transforms in the field of image processing, two filtering techniques will be investigated here as examples of noise reduction of color images. The first one, the Gaussian band-pass filter, deals with the problem of reducing the noise in color images. The Gaussian filter will be used as an example of noise reduction techniques. The second technique will address the problem of edge detection in color images.

A.    Noise reduction using gaussian filter and quaternion fourier transforms

The transfer function of the Gaussian low pass filter in two-dimensions is given by:

H(u,v) = e-^"^^/2a2                          (18)

Where a measure of spread about the center. Let a = D_o , then :

H(u, v) = e " ^D2(M,p)/2D ° ²                                 (19)

where Do is the cutoff frequency.

Since Gaussian filters have the very nice mathematical property that a Fourier transform of a Gaussian is a Gaussian, we should get exactly the same results as when using a linear Gaussian spatial filter. And therefore, it does not incur the ringing effect in the spatial domain of the filtered image. The derivation of a Gaussian band-pass filter starts from the low-pass filter:

H_LP(u,v) = _e - ^D2 ( ^M,v) / ^2D2                                (20)

And the high-pass filter:

H_HP(u,v) = 1 - e " ^D2(M ' ^v)/2D H                         (21)

And, the band-pass filter:

H_B p (u,v)= H lp (u,v)* H hp (u,v), D l > D h (22)

Where   DL and DH are the cutoff frequencies of the low and high pass filters respectively.

Images are often degraded by noises. Noise can occur during image capture, transmission, etc. Noise removal is an important task in image processing. Image Noise is classified as Amplifier noise (Gaussian noise), Salt-and-pepper noise (Impulse noise), Shot noise, Quantization noise (uniform noise), Film grain, on-isotropic noise, Speckle noise (Multiplicative noise) and Periodic noise. Accordingly, the images presented in Fig.3 demonstrate the effect of applying the Gaussian filter to these images using the previously described quaternion Fourier transform method. The image in Fig.3a is used as test image and is exposed to different types of noise as following:

• •    In Fig.3b-1, Gaussian zero mean noise with 0.01 variance is added to the original image. The produced image is transferred and represented as quaternions numbers which in turn is transferred to the frequency domain using the fast quaternion

Fourier transforms. The product is then multiplied element-by-element with the Gaussian filter. The filtered image is then obtained simply by computing the inverse quaternion Fourier transform of the obtained product yielding to the image represented in Fig.3b-2.

• •    In Fig.3c-1, Salt & pepper noise with 0.05 noise density is added to the original image. The previous procedure is applied to this image yielding to the image represented in Fig.3c-2.

• •    In Fig.3d-1, Speckle uniformly distributed noise with mean of 0 and variance 0.04 is added to the original image. The previous procedure is applied to this image yielding to the image represented in Fig.3d-2.

a) Original image

b) The original image (left) with Gaussian zero mean noise and its filtered image (right). PSNR = 20.284601

d ) The original image (left) with Speckle uniformly distributed noise and its filtered image (right). PSNR = 20.284069

Fig.3: The results of applying the Gaussian filter to color image based on the quaternion Fourier transforms.

B.    Image qualty estimation

To estimate the quality of the filtered image, the Peak Signal to Noise Ratio (PSNR) is computed. PSNR is the value of the filtered image with respect to that of the noisy image. The value of PSNR and RMSE (Root Mean Square Error) for the proposed method is found out experimentally. The PSNR and the Root Mean Square Error of the retrieved image can be calculated by using the following equations:

PSNR = 20 log io Ol^                     (23)

where

ЕГ-i \xt-x_t |

RMSE = 1=^  ---

• 3 r c

X i and Xt represent the original and the estimated image vectors respectively. r and c represent number of rows and columns of the image respectively.

Figure 5 shows the results of applying the Gaussian band-pass filter in the quaternion spectral domain to the quaternion fast Fourier transform of an image (Fig.4). The higher cutoff frequency of the filter is changed gradually from 110 down to 20. The filtered images are shown in Fig.4-1 to Fig.4-10 accompanied with the image of the filter.

The results show that the PSNR value decreases with each decrease in the higher cutoff frequency of the Gaussian filter. This can be explained as: the noise pixels have high frequency components in the frequency domain, the number of rejected pixels will increase when the cutoff frequency decreases. This leads to a higher difference between the noisy image and the filtered image and accordingly lower PSNR value.

Fig.4 The original noisy image used as test image yielding to the images in Fig.5

Fig.5 The results of applying the Gaussian band-pass filter to the noisy image of Fig.4 with different cutoff values (part-2).

6:

D 0 =0 D 1 =60

PSNR= 20.67

IV.    Conclusion

The Fourier transform of Hypercomplex provides a tool to analyze color images in the whole view. Color images can be represented mathematically as quaternion valued images which can be transformed into the frequency domain using the Quaternion Fast Fourier Transform (QFFT) allowing different image processing techniques to be carried out. The advantage of the quaternion representation for color is that it combines a color 3-tuple (RGB) into a single Hypercomplex number.

• ^7:        This work demonstrates the application of the Gaussian

D0=0 D1=50

PSNR= 20.14 band-pass filter on the basis of QFT. Filtering in quaternion frequency domain allows higher color information accuracy to be achieved because a color is treated as an entity.