Introduction . The implementation of the potentialities included in the design of the combine harvester, achievement of high quality performance of harvesting and productivity are only possible with a correct technological adjustment of working units and observance of operating rules. Complex and changing environmental conditions grain harvesters operate under require the operator to find optimal solutions promptly. Non-optimal decisions, made in the field, downtime due to technical and technological reasons result in substantial loss of resources and potentialities [1].

To develop optimal algorithms of technological adjustment, it is necessary to know accurate values of environmental factors, as well as regularities between adjustable parameters and environmental factors. These interrelationships are quite of-

The work is done on the thematic research plan of the RF Ministry of Education and Science no. 1.12.12; state registration no. 01201255338.

^Работа выполнена по тематическому плану Министерства образования и науки РФ № 1.12.12; № госрегистрации 01201255338.

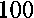
ten known approximately. As a result of the operator’s inability to perform technological adjustment, the harvester operates with unregulated working units and with the exceeded level of grain loss.

There are some investigations where the problem of the technological adjustment is solved with the help of mathematical modeling, in particular, using regression models [2 – 4]. However, the application of the given approach has considerable drawbacks, and its application is limited. Among the reasons reducing these models application, we can mention low reliability of the obtained results, narrow area of the model validity, and the limited number of channels (of only numerical information). It is obviously difficult to describe the properties of the technological process completely and accurately using previously developed regression models. The authors of the suggested models also note this fact and suggest using equations only for evaluating techniques.

Among formal approaches of developing models, the experimental and statistical approaches using correlation and regression analyses have got greater distribution. To eliminate the drawbacks of the traditional approach, they use empirical formulae developed as a result of processing experimental data [2, 3, 5, 6]. In [6] on the basis of processing experimental material, obtained in the course of testing, empirical dependencies of quality performances were plotted such as loss after the harvester, loss after the thresher, shattering of grain, impurities on the external factors. Such external factors as straw humidity, mass of 1000 grains, harvester speed, crop yield, grain humidity, and others are considered. The feasibility of empirical formulae for forecasting the values of operation quality indicators is a positive property of the given approach. However, it has some drawbacks. The forecast accuracy is determined by the accuracy of the input factors values, fluctuations of which in the experiment are reduced to a minimum. Therefore changes in output characteristics are stipulated, to a great extent, by uncontrolled inputs, and this calls into question the adequacy of the mathematical problem itself. Moreover, in these models it is necessary to take into account correlation factors, and to determine the effect of one of the factors with the fixed values of others is rather a difficult problem in the experiment. All this results in that the available correlation-regression models represent rather bulky mathematical constructions (and they don’t always adequately reflect the reality), and their real-time application under complex practical conditions is complicated.

At present, grain harveters rather widely use the facilities of control and management automation. Harvesters are also included into the automated system of “precision agriculture”. Although application of a number of automatic cont rol systems by important working units, devices and systems of the harvester is certainly effective, one can’t help mentioning insufficie nt development and operational capability of some of them. Besides, the available automatic systems mainly solve the problems of the harvester movement control and don’t provide decision -making support for the operator when performing technological adjustment of the harvester working units.

Problem definition . Complexity of the harvester operation system results in that its mathematical model is difficult to be constructed in the traditional sense, and the available approximate models are practically unsuitable in the field. This makes us turn to fuzzy modeling which methodology is directed to fuzzy information, its approximate character, as well as an expert method of forming solutions. In fuzzy models, a linguistic approach is used to formalize real systems, and the relationship among sets of input and output variables is described on the quality level in the form of statements by way of production regulations. Fuzzy models have already proved to be good in various areas [7 – 9].

Процессы и машины агроинженерных систем

The problem of selecting an adequate formal language is very important; therefore we should note the advantages of the decision-making process description in a complex multi-level hierarchy system on the basis of the theory of fuzzy sets. This language makes it possible to reflect adequately the essence of the decision-making process itself under fuzzy conditions for a multi-level system, to work with fuzzy limitations and aims, as well as to set them with the help of linguistic variables. Thus, a mathematical apparatus of the theory of fuzzy sets is expedient to be used as the main tool for describing a multi-level hierarchy system – a grain harvester, processes of decision-making and control of technological processes in complex systems. The suggested approach of the decision-making processes modeling when performing technological adjustment and updating of technological adjustments of the harvester working units on the basis of fuzzy models meets the requirements of the system analysis – consistency of consideration of a complex hierarchy system (harvester) on the basis of accounting basic elements and processes in the system of relations between them, and the sufficient degree of simplification during modeling allowing reflect a real process adequately and take into account the determining factors in this system.

Problem solution . The technique of modeling the decision-making process while performing technological adjustment of the harvester is based on the application of mathematical apparatus of the theory of fuzzy sets [10, 11] and contains the stages of fuzzification, composition, and defuzzification.

At the stage of fuzzification, it is necessary to give the conditions of problem solving in a linguistic form. At the stage of composition, all the fuzzy sets specified for each term of each input variable unite, and the sole fuzzy set is formed – a value for each output linguistic variable (LV). As a result of applying the rule set – fuzzy knowledge base – we calculate the truth value for supposition of each rule on the basis of certain fuzzy operations corresponding to the conjunction or disjunction of terms in the left part of the rule. The main point of the defuzzification stage is in working out, on the basis of fuzzy logic output, certain recommendations on determining certain values of the adjustable parameters of the machine.

Let us consider the problem when depending on possible values of the input situation ( 4 j ) an expert draws a conclusion about the output situation ( В j ) (about the values of the adjustable parameters). Let { X } denote a set of values of input parameters, i.e. value part of the environmental factors which substantially influence the value of the output parameter V (adjustable parameter). To solve the given problem, it is necessary to solve the questions of modeling expert information about relations of characteristics under consideration, and also about the decision-making procedures.

According to the logic- linguistic approach [12, 13], we have developed the models of input and output characteristics X, V in the form of semantic spaces and corresponding to them membership functions (MF):

{ X i , Т ( X i ), U , G , M }, {РV , T V , V , G V , M V },

ЦR ( x 1 , x 2 , …, x i ,) е(0; 1),

ЦR ( v 1 , v 2 , …, v j ,) е(0; 1).

As a result of the analysis, a generalized domain model “preliminary adjustment of the harvester” is co nsidered in the form of the fuzzy relations composition of the semantic spaces under consideration.

R = X -> V .

where R is a fuzzy relation between environmental factors and adjustable parameters R{ X i , т ( X i ), U , G , M }‹ рV , T V , V , G V , M V ›( x , v ) XV .

Relation R can be regarded as a fuzzy set on the direct product XV of the complete space of suppositions X and the complete space of conclusions V .

As a result of fuzzification of the studied characteristics, MF of the adjustable parameters and external factors are plotted. Let us consider normal fuzzy sets for which height is equal to 1, i.e. upper bound of the membership function is equal to 1 ( sup цA(x) -1 ). Fuzzy sets can be both unimodal, i.e. only on one x of E, and possessing an area of tolerance. To describe xE the terms, we used typical functions of the triangle and trapezoidal type [14].

The problem solution of choosing adjustable parameter values is considered by an example of selecting the rotational speed values of the threshing drum. It is known that this parameter is significally affected by the following environmental factors: crop yield, grain humidity, rough straw, grain dockage [15]. The analysis of the subject domain allowed us to define a linguistic description of the external factors under consideration [12]:

LV tuple « Crop yield - 50 » has the form:

CY ={CYL50, CYA50, CYM50}.

LV tuple «Stand of grain humidity» has the form:

SGH ={DrSG, NorSG, HumSG}.

LV tuple «Rough straw» has the form:

RS ={SmRS, NorRS}.

LV tuple «Stand of grain dockage» has the form:

SGD ={LwSGD, LgSGD, %}.

Table 1 presents the values of MF parameters of the external factors under consideration.

Table 1

Values of the MF parameters a, b, с [14] for the external factors

	Values of NF parameters
Kind of the term	Crop yield – 50	Stand of grain humidity	Stand of grain dockage	Rough straw
Left	a = 44 b = 50	a = 11 b = 14	a = 10 b = 30	a = 45 b = 55
Central	a = 44 b = 56 c = 50	a = 11 b = 17 c = 14
Right	a = 50 b = 56	a = 14 b = 17	a = 10 b = 30	a = 45 b = 55

The tuple of the output LV “Rotational speed of the threshing drum for wheat - 50” (i.e. for crop yiel d approximately 50 q/ha) has the form:

– 940] >

RSTD ={VLRSTD, LRSTD, LNRSTD, NRSTD, HNRSTD, HRSTD, VHRSTD, rev/min} (fig. 1).

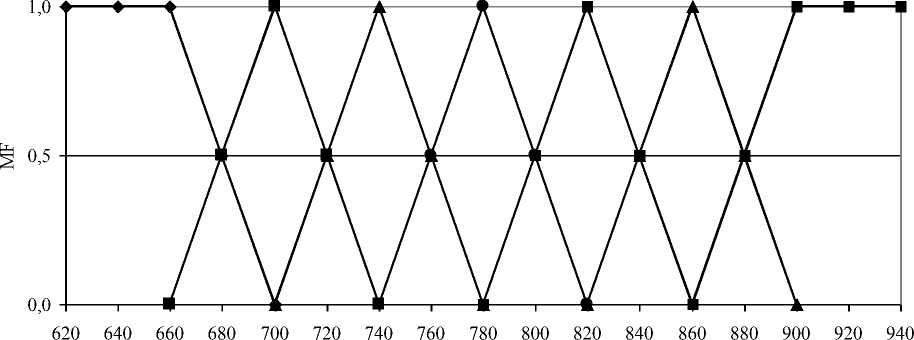
RSTD. rev/min

VL -■- L LN -е- N -■- HN   H —■- VH

• Fig. 1.    Membership functions of LV terms “Rotational speed of the threshing drum for wheat”

With the pre-set system of logical statements for the values of input parameters, the values of the output parameter V are such a set V ₀ ⁽¹⁾ , for each element of which v е V ₀ ⁽¹⁾ a derivation scheme

_L ~ (1)

А – true; '

В – true has the greatest truth degree ц(m1p)    of the fuzzy rule modus ponens which is determined by the expression:

н mp(1) = min{l,[l-piW1 (w ') + Ц V1 (v')],...,[1-ЦWm (w ') + цVm (v')]} .

Процессы и машины агроинженерных систем

The value ц ( _m 1) _p ,(1) is a truth degree of the modus ponens rule for a fuzzy system of expert statements. This concept reflects the correspondence degree of the value of the output parameter V to the value of the generalized input parameter w ’ when expert information is set by the fuzzy system (1). Let us designate the statements < рW is аWj > and < РV is аVj > through A _j and B j . Then the system fuzzy statements will be written in the form of:

	~ (1)		~	~
	L 1 :	if	л 1 , then	В 1 ,
~(1)	~ (1)		~	~
L = <	L 2 :	if	л 2 , then	В 2 , .	(1)
	... ~ (1)		~	~
	L m :	if	л m , then	вm
Fuzzy statements correspond to the general	form:

~~

A j :<р W is а W_j >  и B_j :<1 V is а V j , where а _V , а _V* ^а_V are corresponding values of the terms of the output LV [16].

In the basis of the solutions output mechanism of intelligence information system there is a model of the given subject domain representing a composition of fuzzy relations of semantic spaces of input and output parameters.

An expanded form of the fuzzy logic inference for the system of knowledge in the form of (1) can be presented as follows:                                                                                                             103

Ц B- =kKjJ Ц Bkj yj ) iI \ц Aki ( x _i ’)) . k е Kj е J       iI

As a result of the analysis of the subject domain, a knowledgebase is created. A logic inference of the solution is based on it. A fragment of the knowledgebase is presented below:

• 1.    If (crop yield is less than 50) and (rough straw is low) and (dockage is low) and (stand of grain humidity is dry) then (rotational speed is very low) (1)

• 2.    If (crop yield is less than 50) and (rough straw is low) and (dockage is low) and (stand of grain humidity is normal) then (rotational speed is less than nominal) (1)

• 3.    If (crop yield is less than 50) and (rough straw is low) and (dockage is low) and (stand of grain humidity is damp) then (rotational speed is nominal) (1)

• 36.    If (crop yield is more than 50) and (rough straw is high) and (dockage is high) and (stand of grain humidity is damp) then (rotational speed is very high) (1).

At the stage of defuzzification, accurate values of the resulting LV are calculated. For these calculations, a “cent er of gravity” method is used [17]. This method is implemented in Matlab with the help of Fuzzy Logic Toolbox a pplication package, or with the help of approximation technique [18] possessing rather high accuracy. For the fuzzy logic inference, we used Matlab, in particular Fuzzy Logic Toolbox application package [19].

Fuzzy inference is an application of a maximin composition as a compositional rule of fuzzy inference, and the operation of taking minimum as a fuzzy implication.

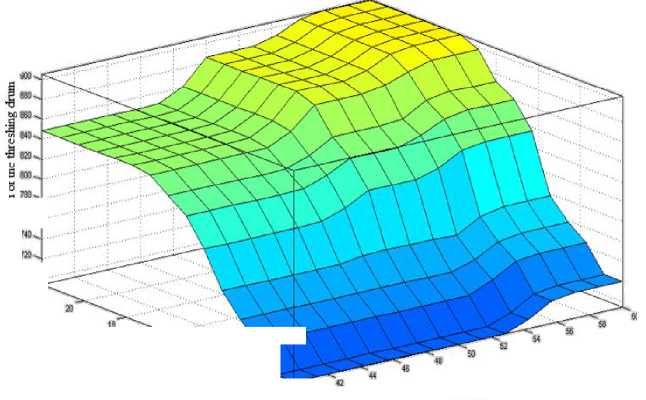
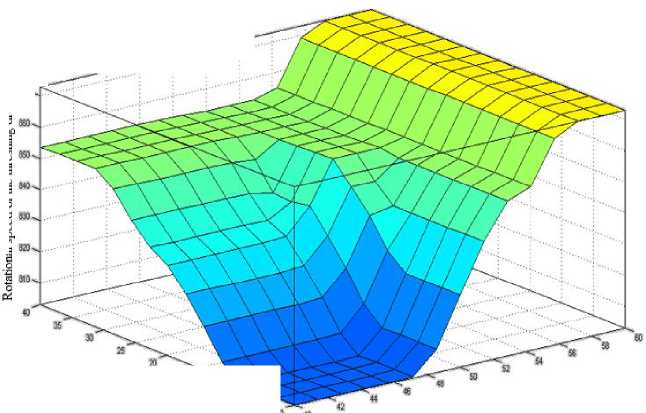
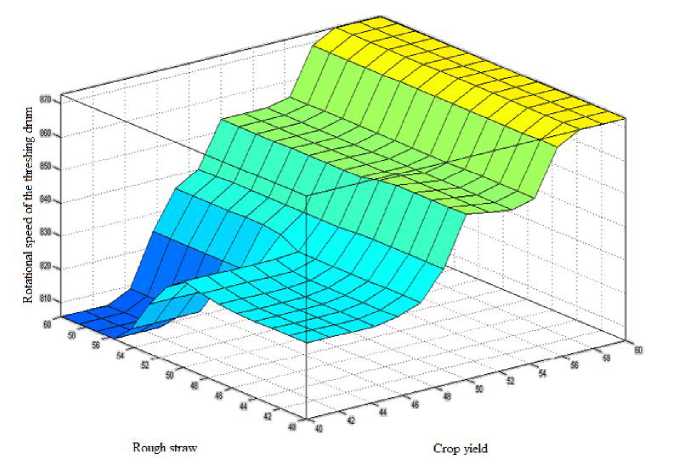
Figure 2 presents surfaces “inputs - output”, and figure 3 presents graphs corresponding to the synthesized fuzzy system of production rules.

10    48 Stand of grain humidity I • csSsB-SSr^O5^ £                           / ^                                   25-\ ■ ci у                                                5 ^                                                                         0  40 Stand of grain dockage b 104

Crop yield ) "-     —         58     ' 56 54 Crop yield )

c)

• Fig. 2.    Response surfaces:

• a) interrelation: rotational speed of the threshing drum-humidity-crop yield; b) interrelation: rotational speed of the threshing drumdockage-crop yield; c) interrelation: rotational speed of the threshing drum-rough straw-crop yield

  
  
  

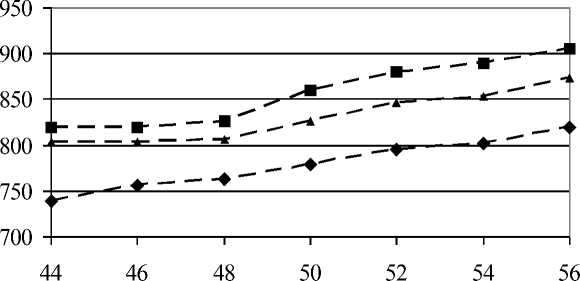
  Grop yield. q/ha

  
  

  ^^^ ^^^™ H=14% — *— H=16% —■- H=18%

  
  

  a)

  
  
  

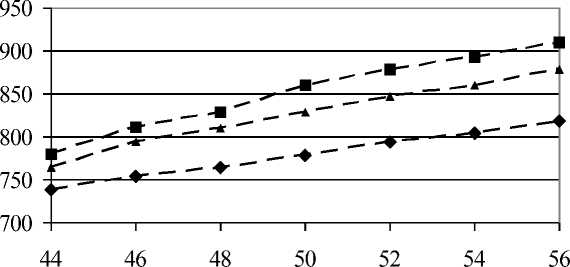
  Grop yield. q/ha

  
  

  H=14%

  
  

  — *— H=16% —■- H=18%

  
  

  Процессы и машины агроинженерных систем

  
  

  b)

  Fig. 3. Dependency of the threshing drum rotational speed on crop yield and grain humidity a) if rough straw is 50%, dockage is 10%; b) if rough straw is 40%, dockage is 0%

  
  

From figures 2 and 3, we can see that the system of fuzzy expert statements adequately describes relations: adjustable parameter – input factors.

Conclusion. The analysis of papers on the theoretical and applied aspects of the theory of fuzzy sets shows that the application of fuzzy models makes it possible to represent the properties of the initial system properly, and to simplify the process of its analysis. The accepted degree of abstraction is the most reasonable as a wider generalization will be fruitless from the point of view of practice. And an insufficient degree of abstractness will result in impossibility of solving the problem – it will be too complicated. In the context of the considered example, the possibility of applying fuzzy inference is displayed. It represents ascending derivations from suppositions to conclusions while solving the problem of the harvester technological adjustment. Modeling of relations “external factor – value of the adjustable parame ter” is carried out by the way of maximum minimum composition, and also by calculating the gravity center of inference results according to the each rule. On the basis of this approach, the formalization of the subject domain is performed, and the mechanism of fuzzy inference of the expert system solutions is constructed for solving the mentioned problem under the conditions of uncertainty.

The knowledgebase and the inference mechanism created on the model basis make up the core of the expert system. The application of this system in the field allows reducing time for technological delays and decreasing the yield loss. Practical implementation of the developed algorithms is creation of software tools for automatic problem solution, intellectual property certificates being obtained for them (№ 2006613272, №2006612454, № 2006613274, № 2007610651). The application of the expert system in practice while performing technological adjustment makes it possible to reduce this period two-fivefold compared to the traditional methods.