Аппроксимация данных, порожденных декартовым произведением
Автор: Беляев М.Г.
Журнал: Труды Московского физико-технического института @trudy-mipt
Рубрика: Математика, информатика, управление, экономика
Статья в выпуске: 3 (19) т.5, 2013 года.
Бесплатный доступ
В работе предложен метод построения аппроксимации для выборок, имеющих структуру декартова произведения произвольного числа многомерных факторов. В подходе используется модель линейного разложении по словарю (некоторому набору) функций, сформированному с помощью тензорного произведения словарей функций меньшей размерности. Для контроля гладкости аппроксимации вводится штраф на изменчивость полученной модели, а коэффициенты разложения по сформированному словарю ищутся оптимальным образом в смысле среднеквадратичной выборочной ошибки. Параметры регуляризации, задающие уровень гладкости модели в каждом из факторов, вычисляются с помощью ошибки скользящего контроля. Специальная структура данных позволяет производить все вычисления со сформированным словарем эффективно. Основанный на предложенном подходе алгоритм успешно используется при решении актуальных прикладных задач.
Аппроксимация многомерной функции по выборке, тензорное произведение, словари функций
Короткий адрес: https://sciup.org/142185924
IDR: 142185924 | УДК: 519.651
Текст научной статьи Аппроксимация данных, порожденных декартовым произведением
Работа, посвящена, задаче аппроксимации, которая заключается в восстановлении некоторой неизвестной зависимости по обучающей выборке — заданному набору пар «точка» -«значение функции в точке» (см. раздел 2). Эта. задача, широко распространена, в инженерных приложениях и является одной из основных составляющих суррогатного моделирования [1]. Для ее решения разработано большое количество подходов [2], которые эффективно работают в широком диапазоне требований прикладной области.
В работе рассматривается специальный случай задачи аппроксимации, в котором множество точек обучающей выборки является декартовым произведением некоторого количества. факторов (множеств) произвольной размерности (см. раздел 2.1). Выборки такого рода, распространены в практических задачах в силу некоторых особенностей задач инженерного проектирования, обуславливающих выбор именного такого дизайна, эксперимента. Большинство методов аппроксимации предназначены для выборок произвольной структуры и не учитывают особенности выборок, порожденных декартовым произведением, что не позволяет в этом случае строить аппроксимацию вычислительно эффективно (обзор методов приведен в разделе 2.2).
Среди многообразия подходов к решению задачи восстановления зависимостей можно выделить классический метод интерполяции двумерных данных с помощью тензорного произведения сплайнов [3], который рассчитан на. выборку, порожденную декартовым произведением двух одномерных множеств (двумерная сетка). Использование этого метода, учитывающего структуру данных, позволяет уменьшить вычислительную сложность построения аппроксимации по сравнению с универсальными подходами.
Реальные задачи зачастую обладают существенно более сложной структурой, чем двумерная сетка. Цель работы — предложить метод аппроксимации для выборок, имеющих структуру декартова произведения с несколькими многомерными факторами, сохранив при этом преимущество в меньшей вычислительной сложности построения аппроксимации. В разделе 3 вводятся некоторые операции с многомерными матрицами, необходимые для дальнейшего изложения. Основные результаты формулируются в разделе 4, где предлагается рассматривать тензорное произведение словарей функций и вводится (в подразделе 4.1) штраф специального вида на изменчивость модели. В подразделе 4.2 представлено утверждение, определяющее условие на существование и единственность решения задачи аппроксимации в рассмотренном классе функций. Предложенный алгоритм построения аппроксимации описан в разделе 4.3, а результаты вычислительных экспериментов приведены в разделе 5.
2. Задача аппроксимации
Рассмотрим задачу аппроксимации функции по конечному набору ее значений в заданных точках. Пусть g — это некоторая непрерывная многомерная функция, g : (X С R^ ^ R^ (в дальнейшем будем рассматривать случай dy = 1, который легко обобщается на случай dy > 1). Будем называть обучающей выборкой S совокупность множества точек S (мош,ности W) и значений функции g в точках из этого множества:
S = {ж G Е,щ = д(хі)У=1 = {s, g(X)}.
Задача 1 (аппроксимации). По заданной обучающей выборке S найти функцию f* G F для некоторого функционального класса F, минимизирующую среднеквадратичную ошибку аппроксимаиуш Q. подсчитанную в ??гонках множества S
f* = argmin(Q(f, S, g(S))) = argmin V(gM - f(ж))2.
f eF f eF t^
Отметим, что эта постановка задачи аппроксимации включает в себя интерполяцию как частный случай при Q(f, S, g(S)) = 0.
Задача 1 позволяет найти такую аппроксимацию f* G F, которая приближает обучающую выборку наилучшим образом. Однако в этом случае может произойти переобучение [2]: значения аппроксимации f * будут значительно отличаться от значений функции g в точках, не принадлежащих S Стандартный подход к решению этой проблемы — введение некоторого штрафа, который ограничивает изменчивость модели и позволяет получить более гладкие решения. Например, в качестве такого штрафа может быть выбрана норма вторых производных f (см., например, сглаживающие сплайны [3]) или норма f в некотором гильбертовом пространстве функций (ядерная гребневая регрессия [4]). В этом случае задача аппроксимации также может быть сформулирована как задача минимизации, но с другой целевой функцией.
Задача 2 (аппроксимации со штрафом на изменчивость). Пусть заданы обучающая выборка S и штрафная функция Рх : F ^ R+- Необходимо найти f* G F для некоторого заданного класса F, минимизирующую функцию ошибки со штрафом R(f, S,g(S)) = Q(f, S,g(S)) + Px(f), а именно:
f * = argmin(Q(f, S, g(S)) + Px(f )) = argmin V(g(ж) - f (ж))2 + Px(f ).
feF feF t^
Заметим, что штрафная функция принадлежит некоторому семейству и задается с помощью параметра А, который определяет вклад штрафного слагаемого в общую целевую функцию. Как правило, Рх зависит от А линейно. Например, задача ядерной гребневой регрессии сводится к следующей оптимизационной задаче:
f* = argmin V(g(ж) - f (ж))2 + A|f ||F.
f eF t^
2.1. Структура данных
Опишем более формально структуру данных, которую мы будем рассматривать в рамках этой работы. Пусть заданы некоторые множества, точек ak = G Xk, ik = 1,...,nk}, Xk е I,1', k = 1,...,К.
Определение 1. Будем называть мносисества ak факторами, а размерность dk каэюдого элемента множества — размерностью фактора ak-
Определим множество точек X как декартово произведение всех факторов: X = ai х a2 х- • -х ак • Тогда элементы множества X — это вектора размерности d = ^k=i dk (а объем этой выборки равен N = пК=і ^-.
X {^ Фгі, ®І2 , . . . , Р к 1 ’ {Pfc G ak }k=1}.
Описанная структура, данных встречается в реальных задачах достаточно часто. Например, распространен случай расположения данных на. многомерной сетке, поскольку он удобен при планировании эксперимента, и обеспечивает равномерное покрытие пространства дизайна точками [!]• в введенных обозначениях такому дизайну соответствует декартово произведение К одномерных факторов.
Также в инженерных приложениях часто встречаются задачи, в которых все переменные можно разбить на. две группы: первая из них соответствует условиям эксперимента, а вторая часть определяет конкретное измерение, сделанное в ходе этого эксперимента. Например, при исследовании аэродинамики крыла, первой группе переменных может соответствовать его геометрическое описание, второй группе — угол атаки крыла, или скорость воздушного потока, а. в качестве выходной переменной может выступать подъемная сила, которой обладает крыло. Сложность изменения значений переменных в первой и второй группах может быть существенно разной (в смысле подсчета, нового значения выходной характеристики для модифицированного входного вектора.). В описанном примере изменение геометрии крыла. — это достаточно дорогая операция (особенно при экспериментах в аэродинамической трубе), в то время как скорость потока, набегающего воздуха, и угол атаки могут быть изменены большое количество раз для каждого крыла. Эта. особенность делает целесообразным использование одинаковой, достаточно плотной сетки значений (набора, векторов) переменных из второй группы для каждого зафиксированного значения вектора. переменных из первой группы. В таком случае выборка, данных будет иметь структуру декартова, произведения с двумя факторами. В некоторых задачах факторизация имеет более сложную структуру и переменные разбиваются на. большее число групп, чем две. Следует заметить, что несимметричная сложность изменения значений переменных из разных групп часто приводит к возникновению анизотропии: переменные из «недорогих» групп переменных (угол атаки) принимают существенно больше различающихся значений, чем переменные из «дорогих» групп (геометрия крыла).
Вернемся к задаче аппроксимации и рассмотрим ее частный случай: пусть множество точек обучающей выборки есть декартово произведение К > 1 факторов, X = ai х а2 х • • • х ак- Тогда область определения функции g также будет декартовым произведением: X = Xi х X2 х • • • х Хк- Поставим в соответствие задачам аппроксимации 1, 2 аналогичные задачи с ограничением на. структуру выборки.
Задача 3. Решить задачу 1 при условии, что множество точек X есть декартово произведение: X = а1 х а2 х • • • х ак-
Задача 4. Решить задачу 2 при условии, что множество точек X есть декартово произведение: X = а1 х а2 х • • • х ак-
2.2. Обзор методов аппроксимации
Для решения задач 1 и 2 существует множество общих подходов, которые могут быть применены к выборкам с произвольным дизайном, в том числе и в случае, когда X есть декартово произведение. Например, это могут быть следующие распространенные методы:
• линейная регрессия [2];
• гауссовские процессы (или кригинг), см. [5];
• разложение по словарю нелинейных параметрических функций, см. [6];
• сплайны (для d = 1), см. [3].
3. Тензорное произведение и многомерные матрицы
Однако универсальность этих методов не позволяет добиться высокой эффективности для частных задач 3 и 4. Сплайны предназначены для решения одномерных задач и по определению не могут быть использованы для размерности d > 1. Линейная регрессия предлагает крайне простую модель, которая может быть востребована при малом количестве данных, но, как правило, выборки, порожденные декартовым произведением, имеют достаточно большой объем, который может доходить до нескольких миллионов точек. Большие значения N затрудняют использование и остальных техник.
Гауссовские процессы имеют вычислительную сложность O(dy N 3 + dN 2), что ограничивает использование этого метода при объемах выборки более 1000 точек. Разреженные гауссовские процессы [7] предназначены для решения этой проблемы и снижают вычислительную сложность до O(dy N m2 + dN m) (где m — это размер некоторой подвыборки из обучающей выборки). Как правило, в качестве m надо брать некоторую не стремящуюся к нулю долго от N, что позволяет расширить область применимости гауссовских процессов лишь до объемов выборки порядка 10 000 точек.
Модели, основанные на разложении по словарю нелинейных параметрических функций (включая искусственные нейронные сети), в основном зависят от объема выборки N линейно (за исключением регрессии на основе радиальных базисных функциях, сложность которой может доходить до O(N 3)). Однако вычислительная сложность этих методов существенно зависит от объема словаря р и размерностей данных d, dy. В зависимости от метода настройки параметров функций словаря сложность может варьироваться от O(Nр (d + dy )) до O(Npdy + Nр2 d? + р3 d3). Зачастую р выбирают пропорционально N, что приводит к (как минимум) квадратичной зависимости от объема выборки. В противном случае зависимость остается линейной, но множитель перед ней принимает достаточно большие значения. Кроме того, необходимо учесть итеративный характер обучения (настройки параметров) таких моделей (количество итераций может доходить до нескольких тысяч), что еще сильнее увеличивает масштабный множитель.
Помимо высокой вычислительной сложности следует отметить еще одну проблему универсальных методов в рассматриваемом классе задач аппроксимации. Большинство из этих методов явно или неявно предполагает, что точки множества X распределены в пространстве дизайна равномерно. Это условие нарушается в случае анизотропных данных (мощности различных факторов существенно отличаются) и построенные универсальными методами модели могут иметь крайне низкую точность в областях, удаленных от точек обучающей выборки, но находящихся внутри выпуклой оболочки множества X. Такая особенность не формализуется строго, однако этот недостаток универсальных нелинейных методов проявляется в подавляющем большинстве реальных задач.
Существует подход, учитывающий наличие структуры декартова произведения в обучающей выборке данных. Этот метод основан на тензорном произведении сплайнов [3] и предназначен для решения задачи интерполяции данных, заданных на двумерной решетке (частный случай задачи 3 для двух одномерных факторах). Вычислительная сложность этого метода составляет O(n3 + n3 + N (тц + T72)dy), г де rii и П2 — это количество точек в соответствующих факторах, пі П2 = N. Так как для сплайнов можно явным образом построить базис, то метод не требует итеративного обучения и константа перед оценкой сложности мала.
В работе будет предложен метод, основанный на. тензорном произведении некоторых наборов функций, построенных в каждом из факторов. Такой подход является обобщением тензорного произведения сплайнов и позволяет как строить аппроксимацию для выборок. в которых X есть декартово произведешк? общего вида (произведение К многомерных факторов), так и решать не только задачу 3, но и более общую задачу 4 со штрафом.
Для изложения предлагаемого подхода, к решению задачи аппроксимации необходимо ввести некоторые определения. В этом разделе будет описано понятие тензорного произведения, а также рассмотрено обобщение матричных операций на К-мерные матрицы.
3.1. Тензорное произведение
Пусть функции /1(ж1) и /2(ж2) определены на Х1 G R^1 и X2 G R^2 соответственно.
Определение 2. Функцию /([ж1, ж2]), определенную на Х1 х Х2, будем называть тензорным произведением функций /1(ж1) и /2(ж2) и обоз начать /1 0 /2, если /([ж1,ж2]) = /1(ж1) /2(ж2).
Несложно показать, что тензорное произведение ассоциативно, коммутативно и билинейно. Кроме того, оно обобщается и на. другие математические объекты. В частности, нас будет интересовать тензорное произведение матриц, которое носит название произведение Кронекера, и обладает как указанными выше, так и другими свойствами [8].
3.2. Многомерные матрицы и операции с ними
Определение 3. Введем обобщение понятия матрицы. Будем называть У К-мерной матрицей с размерами п1 * п2 * • • • * пк, если
У = {Уіі,І2,...,ік, {ік = 1,• • • , пк }к=1}.
Введем операцию развертки К-мерной матрицы вдоль направления к, которое ставит в соответствие многомерной матрице У матрицу У (к) раз мера П г=к п і * п к- Строки матрицы У(к) — это срез значений тензора У размера 1*п к при зафиксированных ik+1 = 1, • • •, і к = 1, І 1 = 1,... ,і к — 1 = 1 іі пзмешіющемся і к = 1,...,пк- В случае обычных матриц (К = 2) операция развертки сводится к транспонированию: У (1) = У т, а У (2) = У.
Стандартные операции (сложение К-мерных матриц и умножение на скаляр) вводятся естественным образом (поэлементно), как и скалярное произведение:
kZ, У) =
Е
Хіх,і2,...,і к У іі,і2,--.,і к •
і1,І2,...,і к
Помимо этих операций введем еще одну: умножение К-мерной матрицы на матрицу вдоль направления. Пусть B — это некоторая матрица размера п к * п к- Тогда будем говорить. что К-мериая матрица. Z размеров П1 * • • • * П к - 1 * п к * П к+1 * • • • * п к — это результат умножения У вдоль направления к на матрицу B, и обоз начать Z = У 0kB, если Z (к) = У (к)В. Отметим. что умножение вдоль отличающихся направлений коммутативно, а вдоль одинаковых может быть сведено к одному умножению:
(У 0kB) 01C = I
(У^С) 0kB, к = I;
У0k(BC), к = I.
Умножение многомерных матриц вдоль направления тесно связано с произведением Кронекера. Пусть У — это многомерна я матрица размера rii * • • • * пк, а В^, к = 1,..., К — матрицы размера п^ *pk- Рассмотрим операцию vec, которая ставит в соответствие многомерной матрице вектор-столбец, содержащий все ее элементы. Тогда справедливо vec(У 01В1 ... 0кВк) = (В1 0 В2 0 ... 0 Вк)vec(У). (2)
Сравним вычислительную сложность обеих частей равенства (2). Для упрощения предположим, что все матрицы В^ квадратные и имеют размер п^ * п^ а N = Пп. Тогда вычисление левой части требует O(N ^п^ ) операций, в то время как для подсчета правой части необходимо O(N2) операций. Таким образом, использование умножения вдоль направления позволяет получить заметно меньшую вычислительную сложность.
-
4. Тензорное произведение словарей функций
Для решения задач аппроксимации 3 и 4 необходимо выбрать класс функций F, в котором будет искаться решение соответствующей оптимизационной задачи. Рассмотрим подход, основанный на тензорном произведении словарей (некоторых наборов функций). Вернемся к методам аппроксимации, перечисленным в разделе 2.2 (сплайны, линейная регрессия, гауссовские процессы, разложение по словарю параметрических функций). Все эти методы аппроксимации объединяет общее свойство: полученную модель можно выписать в виде f(ж) = 52 ^=1 aj0j (ж), гДе ВИД функций 0j (ж) зависит от конкретного метода аппроксимации. Таким образом, аппроксимация f для каждого из этих подходов может рассматриваться как разложение по словарю {0j (ж)}^=1.
Теперь определим класс функций, в котором будем искать решение задач 3 и 4. Введем следующие обозначения для всех к = 1... К:
-
• Hk = {ж^к Е Xk }"fefe=1, Xk 0 Rdfe — фактор декартова произведения;
-
• Ak = {0jk}^к =1 — словарь фуіікщгіі. определенных на Xk-
- Предположим, что словари функций Ak заданы. Сформируем словарь функций, определенных на Xi х • • • х Хк- с помощью тензорного произвелеиия фупкщш из Ak:
-
4.1. Штрафная функция
Значения функции g в точках из X параметризуются индексами 2102 ,...,гк и могут быть представлены в виде многомерной матрицы У с размерами п * п * • • • * пк-
- g(H. ,ж22 ,...,жКк 1) = Ш^.-гк ^ g(X) = У. Н)
Atensor = {^ц 0 ^22 0 • •• 0 ^к , {jk = 1, . . .,Pk }K=1}.
Пусть линейное пространство функций Ftensor состоит из всех возможных линейных комбинаций функций из AtensoT. Выпишем представление некоторой функции f Е Ftensor в общем виде с использованием многомерных матриц:
f (ж) = А 0101 (ж1) 0202(ж2) . . . 0K0K(жк), (3)
где 0k (ж) — это вектор-столбец 'значений фупкщш из словаря Ak в тонко ж. ;.г А — многомерная матрица коэффициентов разложения по этому словарю. Далее мы будем искать решение задач 3 и 4 именно в классе функций Fterasor.
Обозначим как Фk матрицу значений функций словаря Ak в точках из Hk (размер матриц Фk будет равен пk * Pk) и выпишем функцию ошибки Q, используя выражения (3) и (4):
Q^f, X, g(X)) = £ (д(ж) - f (ж))2 = (У -У, У -У), У = А 0^1 02^2 ... 0^к. (5)
жез
Задача аппроксимации 3 сводится к минимизации (5) по f G Ftensor- Рассмотрим более общую задачу со штрафом 4, которая включает задачу 3 как частный случай. Для постановки этой задачи необходимо задать не только класс функций F, в котором будет строиться аппроксимация, но и вид штрафующего слагаемого P\(f )• В вьіборе P\( f ) есть некоторая свобода, поэтому обычно штрафное слагаемое выбирают таким образом, чтобы оно позволяло контролировать изменчивость аппроксимации f и получить вычислительноэффективные формулы. Предложим подход, удовлетворяющий этим соображениям.
В качестве иллюстрации рассмотрим штраф, ограничивающий изменчивость аппроксимации в Xi — первом факторе декартова произведения. В качестве меры изменчивости будем использовать квадрат выборочной нормы второй производной f по ж1, подсчитанной в точках множества X:
p(f ) =
Ш^ЕX = f Е Е «зі,32,..,зк т^Ж (X )^22 (ж2) ../ф^ (жК .
1 1 5 \Ф-,<к 31,-,3к 1 1 /
Теперь обобщим этот штраф и будем ограничивать изменчивость аппроксимации в произведении некоторого числа факторов Х^1 х • • • х Xkq. Введем бинарный вектор Ө, ненулевые компоненты которого будут соответствовать индексам ki,... ,kq, определяющим вид штрафа. Штраф из примера (6) эквивалентен p(f) = pg(f ), где у Ө не равна нулю только первая компонента: Ө1 = 1. Для Ө с несколькими компонситами, отличными от 0. штраф определяется аналогично (6), но порядок частной производной f будет равен не 2, а 2||Ө||о (под L q нормой понимается количество ненулевых элементов). Перепишем выражение (6) для произвольного бинарного вектора Ө в терминах многомерных матричных операций:
Рө (f) = (Л, Л0і(ӨіПі + (1 - Өі)фТфі) ... 0к(Өк Пк + (1 - Өк )ФКФк))• (7)
Каждая матрица П (размера рк * рк) в (7) — это выборочная норма1 вторых частных производных функций словаря Ак. Пусть д2Фк/дж^джт — это матрица значений частных производных функций словаря Ак в точках из а к по компонентам вектора жк, тогда
Пк
dk dk /
∑︁∑︁
1=1 m=1
Э2Фк Әжкджкт
)■(
Э2Фк джк джт
.
Теперь введем вектор параметров регуляризации А размера К * 1, с помощью которого будем взвешивать рө(f ) для разных Ө при формировании окончательного штрафа P\(f )• Каждая компонента Ак будет определять штраф на изменчивость аппроксимации в соответствующем Хк. Пусть Ө — это множество всех бинарных векторов длины К за исключением нулевого. Тогда, определим штрафную функцию следующим образом:
Px(f ) = Е ^Рө(f) П (Ак Өк + (1 - Өк ))). өеө к=1
Введение вектора А дает возможность явно определять относительный вклад ошибки аппроксимации Q^f, X,g(X)) и изменчивости P\(f ) в общую функцию ошибки. Кроме того, использование именно такой параметризации позволяет штрафовать изменчивость в различных факторах по-разному, что может быть крайне востребовано в задачах с анизотропией (мощности факторов Пк сильно отличаются для разных k). Например, если устремить Ак к 0, то в штрафной функции P\(f ) устремятся к нулю все коэффициенты перед слагаемыми, включающие частные производные с использованием жк, и изменчивость в факторе Хк не будет штрафоваться.
4.2. Вычисление оптимальных коэффициентов разложения
Утверждение 1. Решение задачи 4 6 классе Ftensor со штрафом P\(f ) вида (8) существует и единственно, если матрицы ^T Фk + XkПk не выроэюдены. Кроме того, тензор коэффициентов разложения этого решения по словарю Atensor вычисляется по формуле
Л* = У01Ф1Т (^T Ф1 + X1П1)-1 02^2T (^T Ф2 + X2Q2) -1... 0кФкТ (ФК Ф к + X k П к ) -1. (9)
Доказательство. При заданных словарях Ak и, соответственно, известном классе функций Ftensor поиск оптимальной аппроксимации в этом классе сводится к минимизации функции ошибки по коэффициентам разложения. В свою очередь, задача поиска многомерной матрицы оптимальных коэффициентов разложения Л может быть сведена к обычной задаче линейной регрессии. Действительно, пусть Ф — это матрица значений функций из словаря AtensoT в точках X. Тогда выражение (5) для функции ошибки Q может быть переписано в виде Q = (vec(T) — Фvec(Л))T(vec(T) — Фvec(Л)). Штрафное слагаемое из (8) в матричных операциях будет выглядеть как P = vec(Л)TП vec(Л) для некоторой матрицы П (которая подсчитывается на основе (7)). Тогда задача 4 будет переписана как задача поиска оптимальных коэффициентов Л*:
Л* = argmin [(vec(T) — Ф vec(Л))T (vec(T) — Ф vec(Л)) + vec(Л)TП үее(Л)].
Это стандартная задача гребневой регрессии и ее решение может быть найдено явно: vec(Л*) = (ФТФ + П)-1Ф^ес(Т).
Заметим, что матрица Ф может быть подсчитана с помощью произведения Кронекера: Ф = Ф1 0 • • • 0 Фк- Учтем структуру Ф и перепишем второй сомножитель в (10) по (2):
ФTvec(T) = vec(T 0^T 02ФТ ... 0кФК)•(
Выпишем представление штрафной матрицы П, используя (7):
П = ^(Ө1(Х1ПД + (1 — 01)ФТФ1) 0 ••• 0 (Өк(XkПк) + (1 — Өк)ФКФк).(12)
өеө
Теперь упростим первый множитель в (10), используя свойства произведения Кронекера:
(ФТФ + П)-1 = ((ФТ 0 • • • 0 ФК ) (Ф1 0 • • • 0 Ф к ) + П)-1 = ((ФТФ1) 0-- - 0 (ФК Ф к ) +П)-1.
Обратим внимание на вид (12) штрафной матрицы П и примем во внимание билинейность произведения Кронекера:
(ФТФ + П)-1 = ((ФТФ1) 0 • • • 0 (ФК Ф к ) + П)-1 = ((ФТ Ф і + Х1П1) 0 ...
-
• • • 0 (ФК Ф к + Х к П к ))-1 = (ФТФ1 + Х1П1)-1 0 • • • 0 (ФК Ф к + Х к П к )—1 . (13)
Теперь объединим (11) с (13) и перепишем выражение для оптимальных коэффициентов (10), преобразовав его в многомерную матрицу:
Л* = У 01ФТ ... 0кФК 01(ФТ Ф1 + Х1П1)-1... 0к(ФК Ф к + Х к П к )-1.
Используя свойство (1) умножения многомерной матрицы вдоль направлений, получаем итоговую формулу (9).
Условия на существование и единственность следуют из аналогичных условия для обычной гребневой регрессии. Действительно, матрица ФТФ + П представима в виде произведения Кронекера (ФТФ1 + X1 П1) 0 • • • 0 (ФК Фк + Х к Пк)- Это означает, что ФТФ + П не вырождена тогда и только тогда, когда не вырождены все ФТ Фк + XkПк- ■
Рассмотрим вопрос выбора вектора регуляризации А. Применим для его оценки стандартный подход — скользящий контроль (leave-one-out) [2]. Этот метод позволяет оценить ошибку аппроксимации линейной регрессии на тестовых данных, используя только точки обучающей выборки:
N 2
Qioo = ^ (у - ^ ( xi )vec( A-i^ , г=1
где коэффициенты разложения vec(„4-i) оцениваются по выборке, из которой исключена точка {жг,Уг}- Эта формула может существенно упрощена с помощью матричных преобразований [2]:
Qioo
N /
=Е г=1 \
Уг — 0 ( Х і>ес( А )
1 — Li,i
)
L = Ф(ФTФ + Q) 1фТ
Адаптируем формулу (14) к особенностям нашей задачи, приняв во внимание специальную структуру матрицы регрессоров Ф. Это позволит нам воспользоваться вычислительноэффективными формулами, основанными на операциях с многомерными матрицами.
Утверждение 2. Ошибка скользящего контроля при использовании (9) момсет быть подсчитана по формуле
Qioo = (У —У (У —У) * (z —Z0idiag(Li) ... 0Kdiag(LK)) 2); (15)
где L/ = Ф/ (Ф^Фк + А/^к) 1 Фт diag(Lk) — диагональная матрица, совпадающая с диагональю Lk, «I тензор размера п1 * • • • * пк-
Доказательство. Найдем выражение для матрицы L из (14) с учетом специфики задачи:
L = Ф(ФТФ + П) 'Ф Т = Ф10. • .0 Фк (ФТФ1 + А1П1) 1 0 - • -0 (ФКФк + Ак ^к) А1' 0...
••• 0 фк = ФФ1(ФТФ1 + А1П1)Ay'j 0 ••• 0 (фк(фкФк + Ак^к)-1фк). (16)
4.3. Алгоритм построения аппроксимации
Для подсчета, ошибки скользящего контроля необходимы только диагональные элементы матрицы L, которые согласно (16) выражаются через матрицы Lk из (15): diag(L) = diag L1 0 • • • 0 diag(Lк)• Используя связь (2) между произведением Кронекера и умножением многомерных матриц, преобразуем (14) к скалярному произведению многомерных матриц и получаем искомую формулу (15). ■
Вычислительная сложность формулы (15) составляет 0(22Р/ + N )>что позволяет использовать эту оценку ошибки аппроксимации на. тестовой выборке для выбора, вектора, регуляризации А. В силу факторизованной структуры функции Qioo использование метода покоординатного спуска, для ее минимизации будет достаточно эффективным.
В предыдущем разделе предполагалось, что словари А/ заданы, однако это справедливо только для одномерных факторов, в которых можно явным образом построить базис в пространстве сплайнов. Рассмотрим задачу построения словарей А/ по заданной обучающей выборке S. Как уже было указано выше, универсальные методы аппроксимации могут быть представлены как разложение по некоторому словарю параметрических функций. Построение аппроксимации для этих методов сводится к определению оптимальных (в смысле минимизации некоторой функции ошибки) параметров функций, составляющих словарь. Зафиксируем словари А/, к = I и рассмотрим задачу нахождения словаря А/.
Функция ошибки Q в этом случае может быть переписана следующим образом:
nt Pl 2
QU, Д9(Щ = £ £ (g,i * - £ £ о,, 1КШ )...&« )) = il=1 ik ,fe=l jl=1 jk ,fe=l
-
nl Pl 2
-
= £ £ У^1 - £ = ^« )) =trace( ( у (l) - ф і В і) т ( у (l) - ФіBi)). (17) ik,k=l it=1 jt=1
Задача минимизации (17) по функциям {ф,і }p;l=i = Al (точнее, по их параметрам) эквивалента решению задачи 1 по выборке S i = {си , У (l)}. Таким образом, построение словарей Afe сводится к К задачам аппроксимации, которые могут быть решены с помощью универсальных методов.
Сформулируем полный алгоритм построения аппроксимации, предполагая, что обучающая выборка действительно представляет собой декартово произведение с известной структурой.
1) Формируем из значений функции {yi}i=i многомерную матрицу У = 5 (Е).
2) Для всех к = 1,...,К строим аппроксимацию, используя обучающую выборку Sk = {ск, У(к){- Решаем эту задачу с помощью одного из стандартных методов аппроксимации. Выбор метода должен быть основан на параметрах получившейся задачи. Например, для dfe = 1 логично использовать сплайны, а для больших nfe при dfe > 1 — словарь нелинейных параметрических функций.
3) Находим оптимальный параметр регуляризации А*, минимизируя (15).
4) Подсчитываем по (9) коэффициенты разложения „4* по словарто Atensor для А*.
5. Экспериментальные результаты
Рассмотрим предложенный алгоритм с точки зрения вычислительной эффективности. Оценим сложность нахождения словаря Afe в каждом факторе. При решении задачи аппроксимации по выборке Sfe = {ск , У(fe)} размерность у будет достаточно велика и равна N/nk, а объем обучающей выборки составит nfe. Если в к-м факторе словарь строится с помощью сплайнов, то сложность будет O(nfe + nfe(N/nk )) = O(nfe + Nnfe) Заметим, что для повышения вычислительной эффективности можно использовать В-сплайны [3], которые позволят понизить вычислительную сложность до O(nfe + N) за счет ограниченного носителя соответствующих базисных функций. Для гауссовских процессов критически важным является объем выборки, который в силу факторизации существенно сокращается. Вычислительная сложность решения подзадачи аппроксимации в к-м факторе с помощью этого метода будет равна O((N/nk)nfe ) = O(N nfe ). При использовании разложения по словарю параметрических функций в зависимости от метода обучения сложность составляет ОТ O(nfePfe (N/nk )) = O(NPfe ) до O(nfepfe (N/nk)+nkpfe dfe +pfe dfe) = O(N pfe+nfepfe dfe +pfe dfe). Следует заметить, что объем словаря Atensor равен Р = HPfe>что позволяет выбирать достаточно малые pk. Таким образом, учет структуры выборки позволяет получить линейную зависимость от объема выборки для всех методов аппроксимации и уменьшить коэффициент перед некоторыми линейными слагаемыми (в частности, множителями с pfe для последнего метода).
Сложность вычисления оптимальной К-мерной матрицы коэффициентов разложения 4 по (9) будет равна O ^2==! pfe + Е==1 N (nfe + pfe ) Пі=! p i /n^ . Так как для всех методов pfe/п 6 1, то вычислительная сложность не будет превосходить O(2k=i(nfe + N nfe )). При минимизации (15) дополнительная стоимость каждой итерации (по сравнению с вычислением 4) составляет O(2==1 nfe П/=1 p i ) 11 110 превосходит O(N 2,==1nfe )•
Для упрощения анализа будем предполагать, что число точек nfe одинаково во всех факторах и равно N1/К. Тогда наиболее тяжелой операцией будет построение регрессии с помощью гауссовских процессов со сложностью O N1+2/=). Если же использовать другие методы аппроксимации, то сложность не превысит О N1+1/ку Кроме того, если в задаче есть одномерные факторы (а в подавляющем большинстве прикладных задач это условие выполняется), то сложность вычисления У и минимизации ошибки скользящего контроля будет уменьшаться за. счет использования В-сплайнов.
Таким образом, вычислительная сложность метода, относительно объема, выборки будет несущественно превышать линейную, а. константа, перед этой зависимостью будет достаточно мала.
Рассмотрим ряд прикладных задач из области аэрокосмического проектирования. Типичным примером таких задач является зависимость некоторой аэродинамической характеристики от условий полета, и конфигурации объекта. Структуры множеств точек обучающей выборки X рассматриваемых задач представлены в табл. 1.
Таблица!
Факторизация задач
|
Задача |
К |
d |
dk |
N |
Пк |
|
1 |
3 |
3 |
1 х 1 х 1 |
780 |
10 х 26 х 3 |
|
2 |
3 |
5 |
1 х 3 х 1 |
502460 |
679 х 148 х 5 |
|
3 |
7 |
7 |
1 х 1 х 1 х 1 х 1 х 1 х 1 |
540000 |
25 х 12 х 4 х 6 х 5 х 3 х 5 |
Сравним предложенный метод аппроксимации с линейной регрессией (оценка, коэффициентов с помощью гребневой регрессии), разложением по словарю параметрических функций (однослойная нейронная сеть, обучаемая алгоритмом Левенберга—Марквардта [9]) и регрессией на. гауссовских процессах (пакет GPML [10], разработанный автором книги [5]). Для оценки ошибки аппроксимации будем использовать стандартный подход: разобьем выборку данных на. обучающую и тестовую части. Первая из этих подвыборок будет использоваться для построения модели, а. вторая — для определения качества, построенной аппроксимации. Заметим, что тестовую выборку необходимо выделять таким образом, чтобы сохранить структуру декартова, произведения точек обучающей выборки. В качестве ошибки аппроксимации будем использовать среднеквадратичную ошибку, нормированную на ошибку аппроксимации константой (#Х — мощность множества X):
КёёэУё—^ҒУЁУё 1 ^
E(f,X,g(X)) ^ E _ _( x)) 2 , g(X) #x E*)-
2t^
Будем подсчитывать ошибку не только на. тестовой выборке, но и на. обучающей, а. также учтем время обучения модели. Построение аппроксимации с помощью регрессии на. гауссовских процессах для задач 2 и 3 не представляется возможным в силу большого объема обучающей выборки (как было отмечено выше, этот метод требует O(N3) операций и работает разумное время для N порядка тысячи точек). Результаты экспериментов приведены в табл. 2.
Т а б л и ц а 2
Ошибки аппроксимации и время построения модели
|
лин. регр. |
нейрон, сети |
гаус. проц. |
предл. подход |
|||||||||
|
t |
Etr |
Etest |
t |
Etr |
Etest |
t |
Etr |
Etest |
t |
Etr |
Etest |
|
|
1 |
0.003 |
0.81 |
0.65 |
12.5 |
0.04 |
0.38 |
28.0 |
0.002 |
0.42 |
0.11 |
0.05 |
0.12 |
|
2 |
0.08 |
0.83 |
0.84 |
9500 |
0.048 |
11.6 |
^^~ |
_ |
_ |
74.5 |
0.021 |
0.022 |
|
3 |
0.02 |
0.14 |
0.13 |
3800 |
0.002 |
0.003 |
^^~ |
_ |
_ |
2.96 |
0.0003 |
0.0009 |
Заметим, что увеличение ошибки на тестовой выборке по сравнению с обучающей в задачах 1 и 2 для универсальных нелинейных методов аппроксимации связано с анизотропией данных. В силу существенной неравномерности распределения точек по пространству дизайна построенные этими методами модели обладают нерегулярным поведением, см. пример среза аппроксимации гауссовскими процессами для задачи 1 на рис. 1. Схожая проблема возникает и для искусственных нейронных сетей в задачах 1 и 2. В то же время предложенный метод построения аппроксимации позволяет получить качественную аппроксимацию не только для задачи 1 (рис. 2), но и для более сложных зависимостей, см. срез построенной модели для задачи 2 на рис. 3. Истииная функция f (ж) в задаче 3 имеет не очень сложную структуру, что косвенно помогло избежать резкого скачка ошибки на тестовой выборке для искусственной нейронной сети, хотя метод все же уступил в точности предложенному подходу. Также следует отметить время построения моделей — для предложенного подхода оно существенно меньше, чем для универсальных нелинейных методов аппроксим ации.
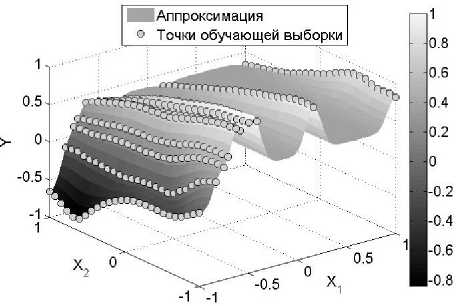
Рис. 1. Регрессия на гауссовских процессах: срез модели в задаче 1
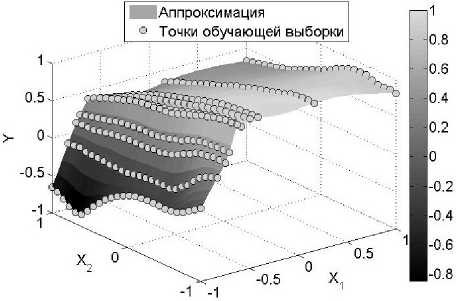
Рис. 2. Предложенный подход: срез модели в задаче 1
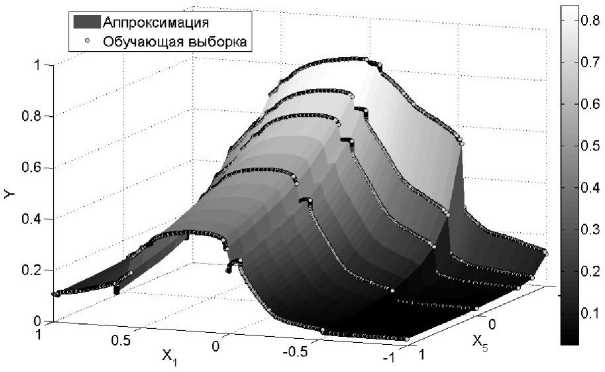
Рис. 3. Предложенный подход: срез модели в задаче 2
6. Заключение
Предложенный в работе метод формирования словаря с помощью тензорного произведения позволяет как свести одну задачу аппроксимации к ряду более простых, так и получить богатый класс функций, способный хорошо приближать сложные многомерные зависимости. Изменчивость модели ограничивается с помощью штрафа специального вида, который построен таким образом, чтобы дать возможность контролировать гладкость модели в каждом факторе независимо от других. Для нахождения оптимальных коэффициентов разложения получены вычислительно-эффективные аналитические формулы.
Низкая вычислительная сложность алгоритма, позволяет быстро строить модели даже для крайне больших объемов выборки, а. контроль гладкости полученной модели успешно решает проблему анизотропии, характерную для прикладных задач. В качестве основного недостатка, можно отметить существенное ограничение на. структуру выборки, которое, впрочем, выполняется для многих задач инженерного проектирования. В частности, предложенный подход был успешно применен для решения ряда, актуальных задач из аэрокосмической отрасли.
Работа, выполнена, при поддержке Лаборатории структурных методов анализа, данных в предсказательном моделировании, МФТИ, грант правительства. РФ дог. 11 .G34.31.0073.
Список литературы Аппроксимация данных, порожденных декартовым произведением
- Forrester A.I.J., S´obester A., Keane A.J. Engineering design via surrogate modelling: a practical guide. -New York: Wiley, 2008.
- Tibshirani R., Hastie T., Friedman J. The elements of statistical learning: data mining, prediction and inference, 2nd edition. -New York: Springer, 2009.
- de Boor C. A Practical Guide to Splines, 2nd edition. -Berlin: Springer-Verlag, 2001.
- Sch¨olkopf B., Herbrich R., Smola A. A generalized representer theorem//Computational Learning Theory. -2001. -V. 2111. -P. 416-426.
- Rasmussen C.E., Williams C.K.I. Gaussian processes for machine learning. -Cambridge: MIT Press, 2006.
- Беляев М.Г., Бурнаев Е.В., Любин А.Д. Методика формирования функционального словаря в задаче аппркосимации многомерной зависимости//Сборник докладов конференции «математические методы распознавания образов «ММРО-15». -2011. -С. 146-149.
- Бурнаев Е.В., Янович Ю.А. Разреженные гауссовские процессы//Труды 54-й научной конференции МФТИ «Современные проблемы фундаметальных и прикладных наук». -2011. -Т. ФУПМ-2. -С. 85-86.
- Graham A. Kronecker Products and Matrix Calculus: With Applications. -New York: Wiley, 1982.
- Matlab Neural Network Toolbox. http://www.mathworks.com/products/neural-network/index.html
- Gaussian processes for machine learning toolbox. http://www.gaussianprocess.org/gpml/code/matlab/doc/index.html


