Аппроксимация функций плотности распределений с тяжелыми хвостами методом Прони

Введение. Метод Прони

Метод Прони – это метод моделирования выборочных данных в виде линейной комбинации экспоненциальных функций (экспонент). При помощи данного метода осуществляется аппроксимация функций с использованием некоторой детерминированной экспоненциальной модели [1].

Пусть статистические характеристики интервалов времени между пакетами и случайные длительности обслуживания подчиняются распределениям с «тяжелыми» хвостами: Вейбулла, Парето, логнормальное. Необходимо найти аппроксимацию этих законов рядами экспоненциальных функций.

Функция распределения Вейбулла имеет вид:

F(x) = l-e р ; х > О, а > О, Р > О, где – параметр формы;   – масштабный пара метр [2], которому соответствует плотность распределения:

.                        (1)

Используя метод Прони (общего вида), аппроксимируем функцию ПРВ Вейбулла суммой экспонент [3].

Выберем известные значения (отчеты) функции при

Будем искать аппроксимирующую функцию V^;

к

± jo где               .

Пусть функция     такова, что существуют коэффициенты [3]

q ^,(1-, ... ct_](; X।,X2 ... Х_к и СГ|,сг₂ ... ст_к, при которых сумма в (2) интерполирует в узлах            Пусть многочлен

1 + dxz + diZ1 +...+dkz (3) /I ± jo имеет нулями числа Z[ = e 1 1, I = 1; 2... k. Тогда для каждого j-V^.-.k имеет место равенство [3]:

JU') + dJU +1) + -+ «(7 + ^) = 0 . (4)

Решим систему (5) при известных значениях fUY найдем коэффициенты d и затем вычислим нули z₍ , используя многочлен (3).

Отсюда найдем искомые значения величин:

2_Z = In z ; cr, = argz_z, I = 1; 2 ... k. (5)

Если значение 2_;>0, берем его со знаком минус. Преобразуем (2) в следующем виде. Если 2 I – экспонента с вещественным показателем, то соответствующее слагаемое оставим без изменения. Если _2l и z_m образуют комплексносопряженную пару \ ± J^z, то заменим Z[ на

X X e 1 sin t^ , zux на e 1 scosg.

Для упрощения примем x, = i, тогда по известным значениям z_f и f (i) найдем коэффициенты h , решив систему уравнений

к

/(0 = 52 h^ , i = 1... N.

z=i

Алгоритм аппроксимации функцииПРВ с помощью метода Прони

Для аппроксимации произвольной ПРВ методом Прони необходимо выполнить следующие действия.

• 1.    Решить систему уравнений (4), чтобы найти коэффициенты ^к .

• 2.    Найти нули функции z i по формуле (3).

• 3.    Вычислить через (5) коэффициенты X^ G(.

• 4.    Решить систему уравнений (6), найти коэффициенты И и записать выражение (2).

Реализуем данный алгоритм для функции ПРВ Вейбулла fw (1) при Ct = 10 И /3 = 2 (см. рис. 1). В нашем случае рассматриваем отчеты

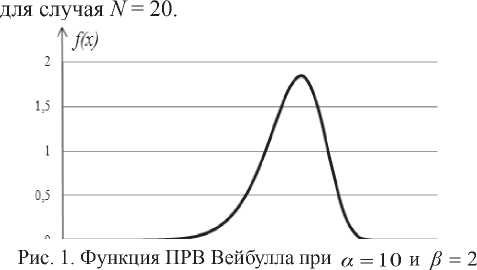
Численные значения искомых коэффициентов представлены в таблице 1.

Таблица 1. Значения коэффициентов ПРВ Вейбулла

/	Искомые значения
	X;	а/	h,
1	-0,4318	-1,0001	1,232
2	-0,4318	-1,0001	-556,152
3	-0,4203	-2,8656	-13330
4	-0,4203	-0,2760	-166000
5	-0,3097	0,3813	405,396
6	-0,3097	2,7603	9444
7	-0,2216	2,2225	7111
8	-0,2216	0,9191	-48,22
9	-0,1690	1,3609	1,038
10	-0,1690	1,7807	167000

При построении модели (см. рис. 2) учтено, что аппроксимирующее выражение для ПРВ должно удовлетворять условию нормировки

J ц/^dx = 1. Выражение нормирующей кон-

станты

const =

к h z ln(z )

Z = 1 / z

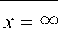
k< №2..

Результат аппроксимации ПРВ Вейбулла ( const = 63371, при нижнем пределе x = 0 и верхнем х = 4) представлен на рис. 2. Аналитическое выражение аппроксимирующей функции имеет вид:

V^ =

52(

X (V - 1)

h e ' cos(cr (x -1))

a-ht e^1^ nsin(crz(x-l))).

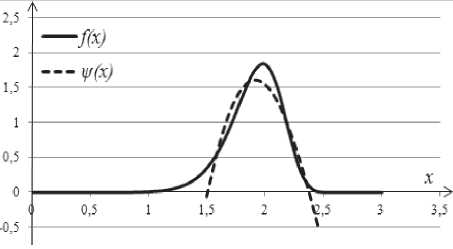
Рис. 2. Сравнение двух ПРВ Вейбулла

После построения аппроксимирующей функции к^) заметим, что некоторые ее значения находятся в отрицательной области. Для удовлетворения свойству ПРВ будем искать исправленное значение И*) из условий

J(^(x),^(x)) = w, Уу(х)~у(х))2 dx +0

x2                                              (8)

+ w2 J(^(x))2t/x^ min,

где C^) – это отрезок, при котором ^/(x) < 0, a w;,w,  – положительные веса, определяемые экспериментально из необходимых условий минимума функционала полученной системы линейных алгебраических уравнений (СЛАУ). Находим СЛАУ, решая d J(^(x),^(x))                           ~

-----------------= U, / = 1   1 и относительно i'll " a

Для нашего случая

J^^x^i/z^x^ = w_x I (^(x) — 22 /г,-,^1- У dx +

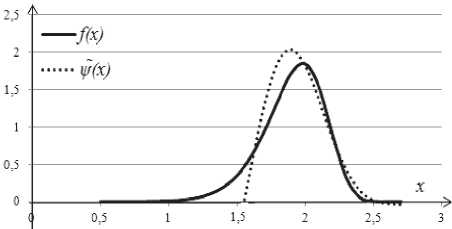
Рис. 3. Сравнение двух ПРВ Вейбулла с учетом условия (8)

Для распределения Парето реализуем аналогичный алгоритм аппроксимации ПРВ методом Прони. Плотность распределения Парето имеет следующий вид (см. рис. 4):

/(x) = -^-(—)“+l,x> p, a>Q, P>0, P x где a – параметр формы, P – масштабный параметр [2].

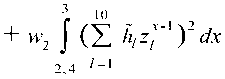
где 1 = 1 ...к; к < NH;

d Jp/fixPyHx))

d h.

з                io

= 2^ jHx)- Hh^ *)z_;' 'dx +

0,5                / = i

з io

+ 2w₇ J( X pz^ ¹ )z_;' 'dx, 2,4 / = i

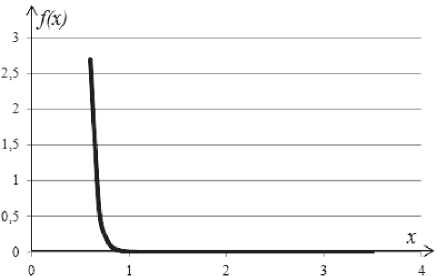
Рис. 4. Функция ПРВ Парето при « = 10 и P = 0,5

io            з

Tji (w f z^{x 1}

/      1 J / i

= 1          0,5

dx -

Jz-

2,4

z‘j dx) — w} ^i//(x)Zj dx.

2,4

Затем подставляем в (7) найденные значения А/ , приравнивая весовые функции Wj “ W2 “ 1’ получаем следующую аппроксимацию.

Погрешность отклонения аппроксимирующей функции ^(x) от /(x) зависит от некоторых величин ^ и Ц. В наше м случае, если учесть при построении функции WU) величины отклонений 4 = 2,5 ; ц = 2,5 ; аппроксимация ПРВ Вейбулла ^to наиболее близка к реальной.

io

V^y = 2 (А/ е^Л'^(л-^-1_/'⁾ cos^^x^ -1 - //) +

+ у _e^^(x^~^x~^ sin(cr_/(x^ -1 - ц)).

Таблица 2. Значения коэффициентов ПРВ Парето

№ nn	Искомые значения
/		Cl	in
1	-1,705	-1,946	7,86E+09
2	-1,705	-1,194	-l,46E+09
3	-1,683	-2,7447	8,37E+08
4	-1,683	-0,396	-5,85E+09
5	-1,706	0,449	-2,74E+07
6	-1,706	2,691	6,67E+08
7	-1,876	1,303	8,40E+05
8	-1,876	1,837	-3,63E+09
9	-3,563	1,570	l,03E+09
10	-8,0721	1,570	2,92E+12

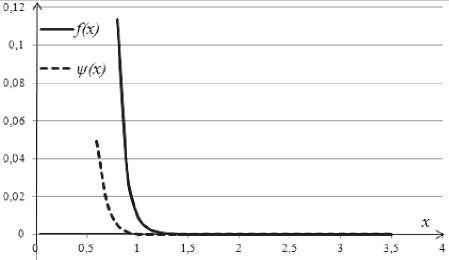
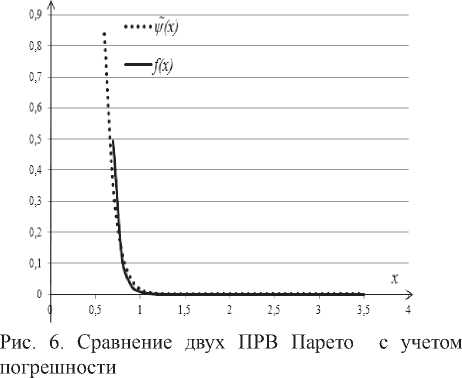
Рис. 5. Сравнение двух ПРВ Парето

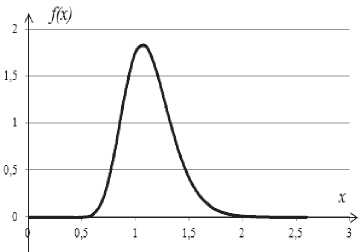
Рис. 7. Функция ПРВ логнормального распределения при ц = 0,1 и <7 = 0,2

Результат аппроксимации ПРВ Парето (const = 8,82912E+14, при нижнем пределе x = 0 и верхнем х = 4) представлен на рис. 5. С учетом отклонений 5 = 1 И JLl = 0,3 получим аппроксимирующую функцию v^, которая наиболее близко приближается к реальной ПРВ Парето

/ (-V) – см. рис. 6.

Для логнормального распределения реализуем аналогичный алгоритм аппроксимации ПРВ методом Прони. Плотность логнормального распределения имеет вид:

e ' ° f (x) = ---,         -, X > 0, - CO < W < oo ст > 0, где о – параметр формы, Ц – масштабный параметр [2].

Результат аппроксимации ПРВ логнормального распределения ( const = 2,52725E+11, при нижнем пределе x = 0 и верхнем х = 3) представлен на рис. 8. В нашем с лучае, если учесть при построении функции ^(x) условие (8) и величины отклонений £ = 1,4 и // = 1,7 ; получим результат, показанный на рис. 9.

Таблица 3. Значения коэффициентов логнормальной ПРВ

	Искомые значения
/	7,	О/	hi
1	-1,182	-1,931	-2,45Е+09
2	-1,182	-1,210	2,38Е+08
3	-1,259	-0,544	1.64Е+09
4	-1,259	-2,597	1,93Е+09
5	-1,3062	0,032	7,78Е+08
6	-1,306	3,108	-8,71Е+08
7	-1,284	2,485	-1,74Е+09
8	-1,284	0,656	-1,52Е+06
9	-1,317	1,864	L50E+09
10	-1,317	1,276	1,66Е+05

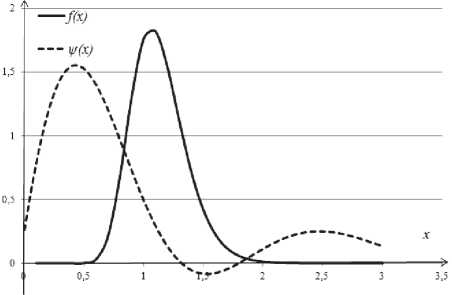
Рис. 8. Сравнение двух ПРВ логнормального распределения

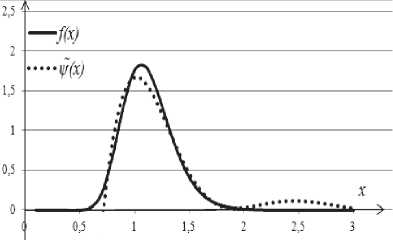
Рис. 9. Сравнение двух ПРВ логнормального распределения с учетом (8)

Заключение

При реализации данного алгоритма точность аппроксимации зависит от количества выбранных на начальном этапе отчетов N функции /и которую необходимо интерполировать. В статье рассмотрены частные случаи для наиболее известных распределений с «тяжелым» хвостом, так как на практике и в многочисленных публикациях доказано, что реальный трафик сети по своим свойствам приближен к ним.

Таким образом, аппроксимация суммой затухающих экспонент может описать функцию ПРВ. Анализ и расчет характеристик мультисервисно-го трафика, поступающего на вход и обслуживаемого в звене системы, является актуальной задачей. Данный алгоритм может также подходить для исследования частных случаев аппроксимации ПРВ, по законам которых циркулируют пакеты трафика в системе СМО типа G/G/1, при условии вещественного значения ^ / . При исследовании функции ПРВ [4] необходимо учитывать свойства самоподобия трафика [5] и произвольный процесс обслуживания.