Аппроксимация распределения плотности вероятности мультимидийного трафика узла МСС

Аппроксимация     распределения     плотности     вероятности мультимедийного трафика узла МСС. Рассмотрим случай обслуживания реального мультимедийного трафика в СМО, представленном узлом MСС.

Вначале введем следующие обозначения плотности вероятности, аппроксимированные суммой экспонент. Обозначим функцию плотности вероятности временных интервалов между прибытием пакетов как a( τ ), а функцию плотности плотности вероятности временных интервалов для обработки пакетов (длины пакетов) как b( ξ ) в соответствии с обозначениями, принятыми .

Мы используем следующие аппроксимирующие выражения плотностей вероятностей временных интервалов между пакетами а ( т ) и времени обслуживания Ъ( ^ ):

а{т}^^аке~акТ, где k =1,...n, n = 5 и k =1,...l, l =5 соответственно.

Пример

Мы аппроксимируем плотности вероятности временных интервалов между прибытием пакетов и временем обслуживания видеотрафика IPTV оборудования абонентского доступа.

Гистограммы плотностей вероятностей видеопотока IPTV на входе приемника IPTV показаны на рис. 3.14, 3.17, 3.18. Гистограмма плотности вероятности временных интервалов между пакетами аппроксимируется распределением Коши, длиной выборки временных интервалов между пакетами i т , где i - моменты прибытия пакетов, i = 1, 2, ..., 100000.

Решая задачу аппроксимации распределения Коши для параметров, задаваемых суммой убывающих экспонент, аналогично тому, как это делается, получаем выражение в виде:

а(т) = ауе~а'т + а2е~О1Т + п3е“"зГ + a4^’^r + a5e~asT, с коэффициентами: // = 5,   ^=0,5240, а2 =-3,3552,   «3 =22,2058,

«₄ =-58,6077, а₅ =65,4504, а_к = — , /и = 0,044.

m

Результат аппроксимации функции плотности вероятности временных интервалов между пакетами видеопотока IPTV и ( т ) показан на рисунке

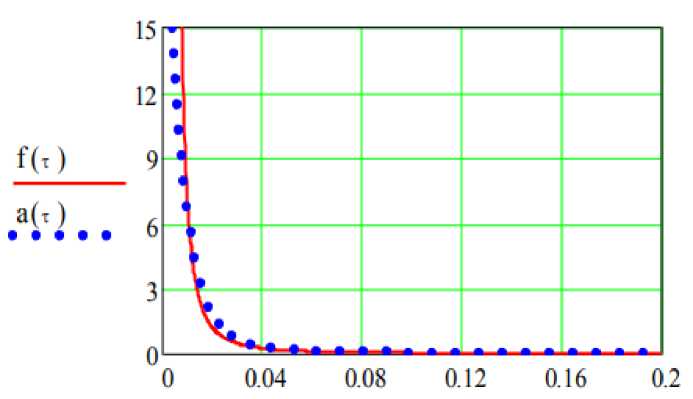
Рис. 1. Плотность вероятностей интервалов времени между пакетами видеотрафика IPTV на входе ресивера IPTV (линия – исходная, точки – сумма экспонент)

График абсолютной погрешности вычисления R( τ ) для функции плотности вероятностей a( τ ) приведен на рис. 2.

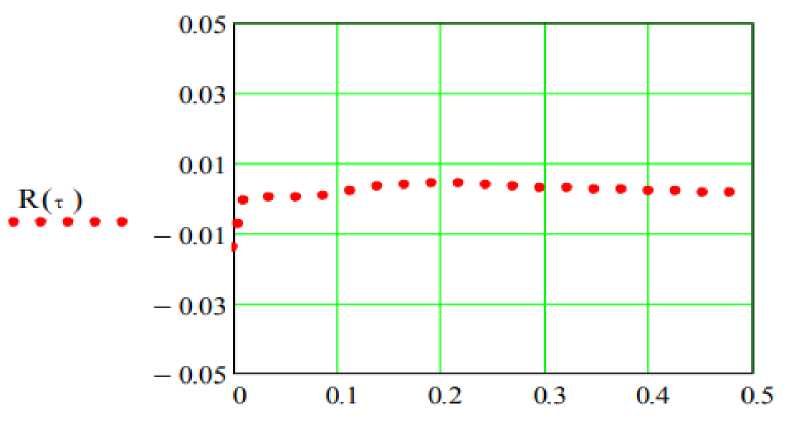
Рис. 2. График абсолютной погрешности R( τ )

Расчет показывает, что  аппроксимация функции плотности вероятности имеет максимальное значение ошибки R (τ ) = 0,01.

Далее мы приближаемся к плотности вероятности временных интервалов для обслуживания пакетов видеотрафика IPTV на входе приемника IPTV j ξ, 104, где j - время прибытия пакетов для услуги, j =1, 2, ..., 10000. На предыдущем рисунке показана гистограмма, выраженная суммой двух функций, в которой второй пик обозначен дельта-функцией для простоты. Осталось аппроксимировать суммой убывающих экспонент первое слагаемое в распределении смеси.

Аппроксимируя распределение Дагума, представленное на рисунке, суммой затухающих экспонент, из получаем выражение:

b(^) = ble № +b-,e   + b3e ^ +b4e ^ + b5e с коэффициентами: / = 5,^ =35,179, b2 =-136,257, b3 =305,545, b4 =-270,161,

/>5 =109,389, Л =-> w = 0,32. m

График аппроксимации суммой затухающих экспонент плотности вероятностей времени обслуживания видеотрафика IPTV b( ξ ) представлен на рисунке ниже:

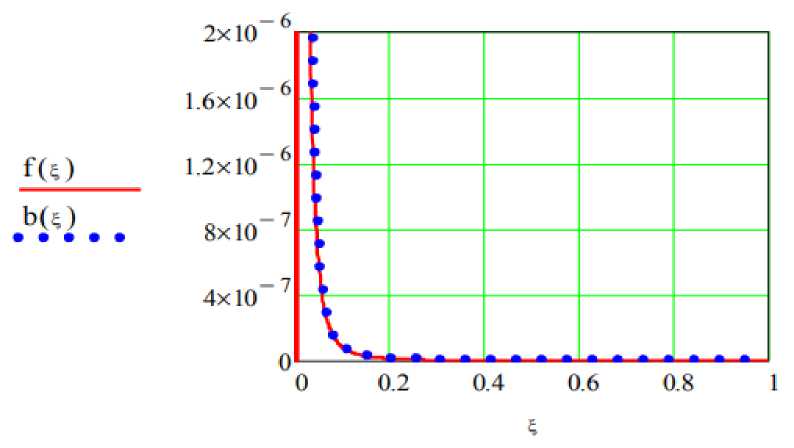
Рис. 3. Плотность вероятностей времени обслуживания видеотрафика IPTV на входе ресивера IPTV (линия – исходная, точки – сумма экспонент)

График абсолютной погрешности вычисления R( ξ ) функции плотности вероятностей b( ξ ) приведен на рис. 4.

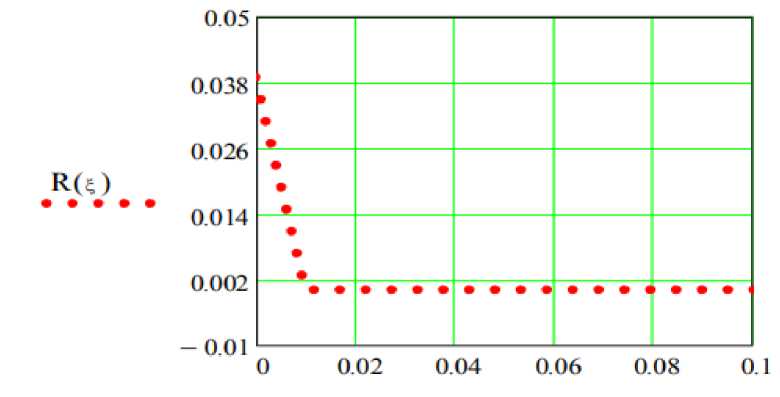
Рис. 4. График абсолютной погрешности R( ξ )

Максимальное значение абсолютной погрешности аппроксимации функции плотности вероятности пакета из суммы разлагающихся экспоненциальных показателей R (ξ) = 0,038 (рис. 4). Таким образом, использование алгоритма для аппроксимации функции случайной плотности вероятности суммой разлагающихся показателей позволяет получить выражения, приемлемые для использования в аналитических методах расчета узлов МСС как в СМО. Дальнейшие исследования показывают, что значения ошибок R (τ) и R (ξ) можно считать удовлетворительными, используя доступные приближения в спектральном методе Линдли решения IE.