Аппроксимация сопряжения кривых Безье с сохранением порядка гладкости и дополнительными ограничениями

В настоящее время конструирование и технологическая подготовка высокосложных изделий невозможна без использования систем автоматизированного проектирования (CAD). При повсеместном применении этих систем постоянно возникают задачи по развитию и совершенствованию «геометрического ядра» – набора программных компонент, отвечающих за математическое представление и преобразования геометрических объектов. Одним из таких преобразований является аппроксимация сопряжения двух заданных кривых Безье, то есть аппроксимация соседних кривых при заранее заданных ограничениях на аппроксимирующую кривую, при этом в общем случае кривые могут быть не смежными. Задачи аппроксимации гладкого сопряжения не смежных кривых являются типовыми при использовании CAD-систем для разработки технологий соединения элементов оболочки внешней поверхности летательных аппаратов, элементов наружной обшивки корпуса судов и т. д. В этих задачах кроме требования гладкости сопряжения, всегда присутствуют заданные из технологических и функциональных требований ограничения на аппроксимирующую кривую.

Кривые Безье находят широкое применение в моделировании, например, в работе [1] приводится обширная библиография областей применения кривых Безье (18 ссылок) и предлагается алгоритм построения замкнутой кривой, проходящей через заданные точки, при этом кривая формируется из сегментов кривых Безье второго порядка. В обзоре [2] рассматриваются многочисленные применения кривых Безье в различных областях производства (траектории движения инструмента, конструирование сложных поверхностей, реинжиниринг, уменьшение объема данных при обмене информацией и т. п.). В [3] строится сплайн, состоящий из кубических кривых Безье, сглаживающий ломаную линию и обеспечивающий непрерывность первой и второй производных. В работах [4, 5] графоаналитическими методами строятся плоские и пространственные кубические кривые Безье, проходящие через заданные точки, в которых эти кривые стыкуются с учетом заданных заранее направляющих векторов и радиусов кривизны. Столь широкое использование кривых Безье объясняется тем [6, 7], что по сравнению с B-сплайнами кривые Безье сохраняют все степени непрерывности во внутренней области определения параметрической переменной и у этих кривых отсутствует вопрос об определении точек смены поддиапазонов параметрической переменной (interior knot values в терминологии [6, 7], breakpoints в терминологии [8]).

Задачи аппроксимации сопряжения кусочнополиномиальных функций возникают в дизайне [9] и при конструировании устройств со свободными поверхностями [10], при этом в современных CAD-системах методы сопряжения обеспечивают не более четвертого порядка гладкости [11]. Кроме этого, при использовании CAD-систем, постоянно происходит обмен графическими данными между CAD- и CAM- ( Computer-Aided Manufacturing ) системами [2], совместная обработка графических объектов и интеграция результатов в графические объекты более высокого уровня, что требует преобразования графической информации, к которому предъявляются требования высокой точности, минимальных потерь и уменьшения объема. Задачи, возникающие при преобразовании графических данных в форматы иных CAD-систем и при уменьшении объема графической информации, рассмотрены в работе [12], в которой указывается на необходимость использования процедуры аппроксимации, которые применяются к полиномиальным и/или кусочнополиномиальным функциям и включают в себя следующие преобразования:

• 1)    понижение степени: аппроксимацию заданной параметрической кривой степени п кривой степени т (т < п);

• 2)    сопряжение: аппроксимацию отдельных полиномиальных сегментов, сегментом одной кривой.

Алгоритмам понижения степени кривых Безье посвящено достаточное количество работ [13–15], включая ставшую классической монографию [8]. Разработки алгоритмов сопряжения кривых Безье приводятся в довольно незначительном числе работ. Так, например, в обзорной работе [2] рассматриваются всего лишь 2 работы по сопряжению кривых Безье [16, 17]. В работе [16] предлагается алгоритм аппроксимации нескольких смежных Безье кривых с различными степенями одной кривой преобразованием параметров заданных кривых к несовместной системе линейных уравнений, которая решается методом псевдообращения Мура – Пенроуза. На аппроксимирующую кривую не накладываются какие-либо ограничения, а также в предлагаемом подходе отсутствует метрика отличия аппроксимирующей кривой от заданных кривых, что является обязательным условием применения метода в геометрическом ядре CAD-системы. В работе [17] предлагается подход к аппроксимации двух соседних (смежность не требуется) Безье кривых с равными степенями одной Безье кривой той же степени, для чего предлагаются две различные метрики, которые минимизируются при наличии ограничений в виде равенств, используя метод множителей Лагранжа. На аппроксимирующую кривую накладываются простейшие ограничения в виде задания точек на заданных кривых, через которые должна проходить аппроксимирующая кривая. Настоящая работа базируется на постанове задачи из работы [17] и является дальнейшим развитием этой работы.

Целью настоящей работы является разработка математических методов сопряжения двух кривых Безье произвольных степеней с сохранением в точке сопряжения порядка гладкости (непрерывности), соответствующего степени заданных кривых, и последующая замена двух сопряженных кривых одной кривой Безье той же степени. При этом на сопряженные кривые и аппроксимирующую кривую могут быть наложены дополнительные ограничения в виде полного совпадения с одной из заданных кривых или прохождения аппроксимирующей кривой через заданные точки и равенства производных в этих точках заданным значениям.

В настоящей работе решаются следующие задачи. Формулируются условия полностью гладкого сопряжения двух кривых Безье произвольной степени с учетом дополнительных ограничений, вводятся две различные метрики разности заданных и сопряженных кривых Безье, выполняется аппроксимация сопряжения как минимизация одной из метрик методом множителей Лагранжа и описывается подход к переходу от двух сопряженных кривых Безье к одной кривой Безье той же степени. В отличие от [17], для решения всех представленных задач предлагается единый подход, основанный на представлении кривых Безье как линейной комбинации базисных функций В-сплайнов, что позволяет решить сформулированные задачи единым методом и воспользоваться для решения задач программными функциями, входящими в геометрическое ядро современных CAD-систем. Это существенно упрощает получение производных всех степеней для кривых и, без существенных изменений в последующем, позволит распространить результаты на задачи сопряжения B-сплайнов. Использование базисных функций В-сплайнов позволяет в предлагаемом подходе выразить равенство производных в точке слияния кривых не через конечные разности, как в [17], а через производные базисных функций, которые в геометрическом ядре современных CAD-систем рассчитываются «автоматически» при расчете базисных функций [8] B-сплайнов. Кроме этого, в отличие от [17], в настоящей работе предлагаются подходы, позволяющие учитывать дополнительные ограничения не только в виде заданной точки на исходной кривой, через которую должна пройти аппроксимирующая кривая, но и такие ограничения, как равенство производных в этой точке производным заданной кривой и «запрет» на изменение одной из заданных кривых (то есть требование полного совпадения аппроксимирующей кривой с одной из заданных). В настоящей работе приводится математический подход к замене двух сопряженных кривых одной кривой того же порядка с сохранением порядка гладкости, что отличает данную работу от [17], в которой приводится вычислительный алгоритм без каких-либо пояснений. Предлагаемые алгоритмы позволяют гладко сопрягать с учетом ограничений как 2D, так и 3D кривые Безье.

Постановка задачи

Заданы две кривые Безье Р(и) и Q(v)1 степени п, представление которых будем рассматривать как ча- стный случай В-сплайнов:

Р(и) = Е^Р . ^Чи), и Е [0,1],                             (1)

Q(v) = V4 o Q i N " (v), v Е [0,1],                          _(2)

где u, v - параметрические переменные; N” - i-я базисная функция В-сплайнов степени п; Р., Q., i = 0, п - контрольные точки (многоугольники) кривых Р и Q соответственно.

Так как кривые Безье рассматриваются как частный случай В-сплайнов, то узловые векторы кривых

(1) и (2) задаются как u, v = 0,... 0 ,0,1, 1,... 1 .

И          и

Если для расчета кривых Безье (1) и (2) используются алгоритмы и программные функции NURBS [8] (Non-Uniform Rational B-Splines), то веса wi, i = 0,п контрольных точек Р., Q., i = 0,п полагаются тожде- ственно равными 1.

Необходимо выполнить сопря пени п, которая минимизирует зада! кение кривых Р(и) и Q(v), то есть определить кривую Безье R(t) стенную метрику d(R,R) между R(t) и R(t), где ” ЧАЧЕ™"©- °stsA- «(0 = . i=o и qOEq.nCA), AStS1. v               i=o где А Е (0,1) - параметр, выбираемый как середина интервала либо пропорционально длинам сторон контрольных многоугольников [6].

Минимизация метрики d(R,R) выполняется на всем диапазоне изменения параметрической перемен ной t Е [0,1].

Нахождение аппроксимирующей кривой R (t) будем выполнять в два этапа.

Этап 1 . Гладкое сопряжение кривых Р(и) и Q(v), то есть расчет новых контрольных точек Р . , Q . , i = 0, п, по которым строятся новые сопряженные кривые Безье Р(и) и Q(v). При этом кривые Р(и) и Q (v) должны удовлетворять условиям полного гладкого сопряжения:

Р(г)(и)|м=1 = Qw(v)L=o, г = cm,(3)

где г - порядок производной (нулевая производная (г = 0) соответствует значению функции).

Кривые Безье Р(и) и Q(v) определяются следующим образом:

Р(и) = V/ Р. N'(u) = V' (Р. + £i) N”(u), и Е [0,1],

_        Q(v) = E”=o Qi N”(v) = V=o(Qi + 6.) N”(v), vЕ[0,1], где £., 6., i = 0, п - приращения координат Р., Q., i = 0, п соответственно.

Этап 2 . Замена без погрешности (абсолютно точно) кривых Безье Р(и) и Q (v) одной кривой Безье R(t) степени п, для чего рассчитываются ее контрольные точки R . , i = 0, п.

На кривые Р(и) и Q (v) (и соответственно на R(t)) могут быть наложены следующие дополнительные ограничения:

1)полного совпадения с одной из заданных кривых:

Р(и) = Р(и), и Е [0,1]

~       ~ Q(v) = Q(v), vЕ [0,1];(7)

2)сопряженные кривые Р(и) и Q(v) должны проходить через заданные точки исходных кривых с сохранением значений производных вплоть до некоторого порядка в этих точках:

(Р^Чи)^) = (Р^Чи)^), кр = 0Д, г1 = 0угр,

(Q^v^^J = (p^v)^^), kq = 0,m, r2 = 0,rq,             (9)

где rp, rq - максимальный порядок производных (как и ранее, нулевая производная соответствует значению функции).

Очевидно, что максимальное значение порядка производных не должно превышать и. Как показано в [17], ограничения (8) и (9) должны удовлетворять условию:

_                  [(Z + 1) + (m + 1)] < (и + 1)

Метрику d(R, R), как и в [17], запишем в двух формах:

1)дискретная коэффициентная норма:

О^Л) = ^^(Не.Н2 + II^H2) ^ min;

2)интегральная квадратичная норма:

O(et,8t) = Jo1(R(t) — R(t))2 dt = £ [(Е^^ЧО)2 + (E^Wto)2] dt ^ min

Метрика (11) минимизирует отклонение контрольных точек P , и Q , от P , и Q_t , i = 0, и. Метрика (12) минимизирует площадь между кривыми P(u), Q (v) и P(u), Q(v).

Таким образом, сформулирована задача полностью гладкого сопряжения, которая состоит в оптимизационной задаче (11) или (12), при наличии ограничений (3), где также дополнительно могут присутствовать ограничения (8) и (9).

Метод

Условия полностью гладкого сопряжения (3) с учетом представления кривых в развернутом виде (4), (5) представляют собой систему (и + 1) равенств:

V . ^- (P . ■ Л . ) V . (1) V . ^- (Q . ■ 5 . ) V . (0;. r = 0^, (13) где М” ^(Г ) (1), V_t ^/(r) (0) - производные порядка r i-й базисной функции порядка и при значении параметрической производной 1 и 0 соответственно.

Использование в (13) производных базисных функций В-сплайнов, в отличие от конечных разностей в [17], позволяет отказаться от довольно сложной рекурсивной процедуры расчета этих конечных разностей, что позволяет существенно упростить построение коэффициентной матрицы системы линейных уравнений за счет единообразия расчетных выражений и воспользоваться существующими в современных геометрических ядрах CAD-систем программными функциями и классами расчета базисных функций В- сплайнов и их производных.

Рассмотрим оптимизационную задачу (11) при ограничениях (13), для решения которой применяется метод неопределенных множителей Лагранжа [18]. Функция Лагранжа имеет вид:

Ь = Е^(Не , Н² + Н5 . Н²) +

_               ■ V -    /'.  V . ^-   (P .   ■ Л . ) V . ' (1)    V . ^-   (Q .   ■ 1> ; V . ;0;|.                             ⁽ )

где Лг, r = 0,и - множители Лагранжа.

Находя частные производные функции (14) по переменным е , , 5 , , Л_г, i,r = 0, и и приравнивая их нулю, получаем систему линейных алгебраических уравнений относительно неизвестных переменным е , , 5 . , Л_г, i,r = 0, и:

= 2е,+E;yo4V4'41) = 0, i = 0^,

Uc £

~^= 25,—ELo^^d)) = 0, i = 0^,

UO £

^ = V.- [(P, + е,Ж"(г)(1) - (Q, + 5,Ж"(г)(0)], r = 07Й.(17)

Выполнив в уравнении (17) перенос слагаемых, не содержащих искомых переменных, в правую часть, получаем:

Е^^Ж^!)— 5Ж;('Ч0)| =—V^IW'd!) ЖЖ^^^      r = 07Й.

Таким образом, получили систему 3(и + 1) линейных уравнений (15), (16) и (18).

Следует указать, что в уравнениях (15), (16) и (18) производные r-го порядка базисных функций (M” ^(r) , r = 0,и) обладают тем свойством, что только (r + 1) базисных функций отличны от нуля [6, 8]. В нашей работе это свойство не используется, что позволяет упростить (сделать более единообразным) заполнение коэффициентной матрицы и вектора правых частей, тем самым упростив программную реализацию соответствующей функции геометрического ядра.

При использовании оптимизационной задачи (12) при ограничениях (13) система линейных уравнений выглядит следующим образом:

ЕЖЖ+Х;Ж,.Ж'Ч1) = 0 , i = G/й,                     (19)

E"^4_i—X ; ^; -o4 V / ^;( ''4 0) = 0, i = 0^,                          (20)

V .' '^ . V .'^d ) 8 . V.^'(0)|   -^[P i N^n-Q i N^)], r = 0,п,        (21)

где интеграл I j _t = 2 / ^ N j (T)N_t(T)dT вычисляется численно.

Дополнительные ограничения

• 1.    Ограничение в виде полного совпадение с одной из заданных кривых.

• 2.    Ограничение в виде «закрепления границ».

• 3.    Ограничение в виде прохождения сопряженных кривых через заданные точки исходных кривых с сохранением производных.

Рассмотрим ограничения (6) или (7), выполнение которых является тривиальным, для чего из оптимизационных задач исключаются соответствующие неизвестные (_£i, i = 0, п при ограничениях (6), либо 8 ^ , i = 0, п при ограничениях (7)) или, применяя другой способ, уравнения (15) и (19) записываются как £ ; = 0, i = 0, п (при ограничениях (6)) и уравнения (16) и (20) записываются как 8_t = 0, i = 0, п (при ограничениях (7)).

Часто встречаемое в реальных задачах сопряжения требование «закрепления границ» (неизменности начальной точки кривой Р(й) и конечной точки кривой Q(v)) реализуется записью первого и 2(п + 1)-го уравнений системы как £_o = 0 и 8₂ = 0 соответственно.

Дополнительные ограничения (8) и (9) в развернутом виде выглядят следующим образом:

Х;Д(Р, + ^Ж^Ч^р) = Z'LoPiNi"(rl)(ukp), kp = 0,1, r1 = 0,rp,

Z?=o(Qi + 8f) <(г2) (vkq) = ZL Qi N^ (vkq), kq = 0^, r2 = 0^.(23)

Раскрыв в (22) и (23) суммы и, выполнив взаимное уничтожение, получаем:

Z”=o £i N”(rl)(ukP) = 0, kp = 0,1, r1 = 0,rp,

Z”=o 8i N”(r2)(vkQ) = 0, kq = 0/m, r2 = 0,rq.(25)

Добавив эти [(Z + 1) + (m + 1)] слагаемые с соответствующими дополнительными множителями Лагранжа в функцию (10) и выполнив по аналогии с (15)–(17) расчет частных производных, получаем систему [3п + (Z + 1) + (m + 1)] линейных уравнений. При использовании интегральной квадратичной нормы выкладки аналогичны.

Расчет кривой R(t)

Переход от двух гладко сопряженных кривых Безье Р(ы) и Q (v) степени п к одной кривой Безье R(t) той же степени выполняется без какой-либо погрешности с помощью расчета контрольных точек R_t, i = 0, п, по которым в последующем строится кривая R(t). Рассматривая расчет кривой R(t) как процедуру, обратную к процедуре разбиения кривой Безье [6, 7, 19], можно записать следующую систему уравнений:

для нечетного п:

p ^ko R ^(ko) (0) = p ^(ko) (0), k0 = 0, [ 2 ], p ^kl R ^(kl) (p) = P ^(kl) (1), k1 = 0, [ 2 ],

где

• [ 2 ] - целая часть числа 2 .

Для чётного п система имеет тот же вид, что (26) и (27), за исключением диапазонов изменения индексов: k0 = 0,]

k1 = c,( 2 -1)

Уравнения (26) и (27) описывают равенство как самих кривых R и Р, так и их производных в начальных точках этих кривых (уравнения (26)) и в точке окончания кривой Р (уравнения (27)). Значения параметра р определяет интервал репараметризации [20], и в последующих примерах его значение было задано как 0,5.

Результаты и обсуждения

Рассмотрим результаты применения представленных выше математических подходов на конкретной задаче аппроксимации сопряжения кривых Безье сохранением порядка гладкости и дополнительными ограничениями.

На рис. 1 представлены две заданные кривые Безье третьей степени, для которых будут выполнены различные виды полностью гладких сопряжений при различных дополнительных ограничениях.

На рис. 2 приведены результаты полностью гладкого сопряжения кривых, представленных на рис. 1, с использованием дискретной коэффициентной нормы (11) без дополнительных ограничений.

На рис. 3 представлен переход от двух гладко сопряженных кривых Безье /(и) и Q(v) (см. рис. 2) к одной кривой Безье R(t).

На рис. 4 представлено решение той же задачи (полностью гладкое сопряжение кривых, при-

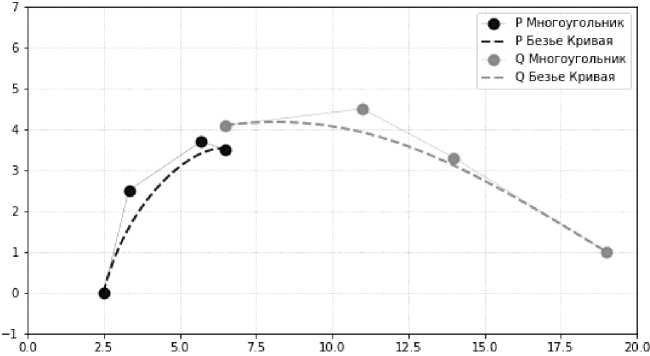
Рис. 1. Заданные кривые Безье Р(и) и Q(v)

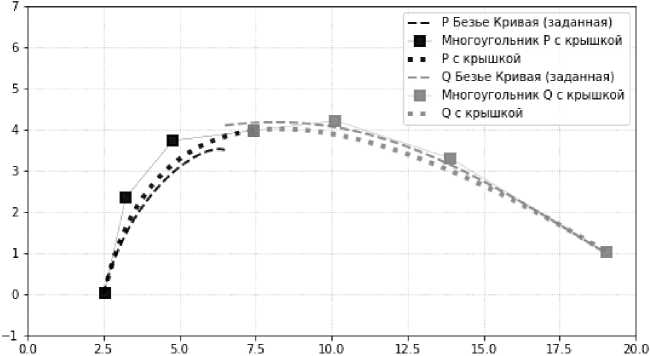
Рис. 2. Заданные кривые ( Р(й) и Q(v) ) и эти же кривые после сопряжения ( Р(м) и Q(v) ) (дискретная норма)

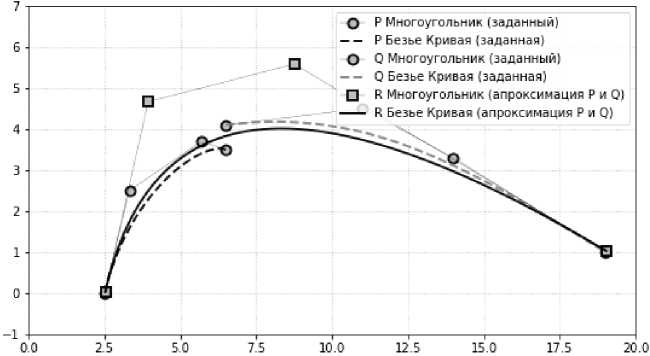
Рис. 3. Замена двух гладко сопряженных кривых (см. рис. 2) одной кривой R(t) (дискретная норма)

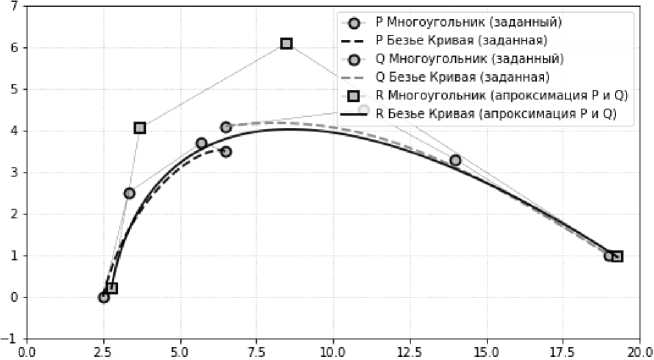
Рис. 4. Замена двух гладко сопряженных кривых (см. рис. 2) одной кривой R(t) (интегральная норма)

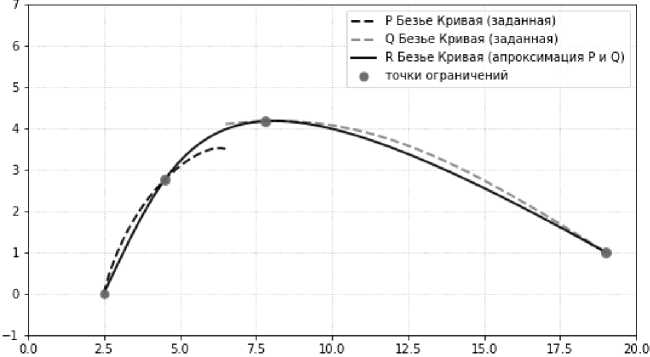
Рис. 5. Сопряжение при ограничениях (28) (дискретная норма)

веденных на рис. 1) с применением интегральной квадратичной нормы (12) без дополнительных ограничений. Как видно из рис. 4, при интегральной норме начальная и конечная точки аппроксимирующей кривой отклоняются от соответствующих точек заданных кривых. Эти отклонения могут быть легко устранены введением дополнительных ограничений в виде закрепленных границ.

На рис. 5 приведены результаты сопряжение для дискретной коэффициентной нормы при сле- дующих ограничениях:

P(v o ) = P(u o ), ы₀ = 0,

P(U1) = P(U1), Q(Vo) = Q(Vo), 0(V1) = Q(V1), и1 = 0,5, Vo = 0,1, V1 = 1,0.

На рис. 6 приведены результаты сопряжения для интегральной квадратичной нормы при последовательном добавлении следующих ограничений при u0 = 0,4:

P(Uo) = P(«o),

P(1)(uo) = P(1W

P(2)(Uo) = P(2)(Uo).

Дополнительное ограничение (29) устанавливает требование прохождения аппроксимирующей кривой (кривой R) через заданную точку u_o на кривой P(u). Совместные ограничения (29) и (30) задают требование прохождения через точку u_o с сохранением первой производной в этой точке. Совместные ограничения (29), (30) и (31) – прохождение через точку u_o с сохранением двух первых производных.

Из сравнения сопряжения без ограничений (см. рис. 4) с сопряжением при различных ограничениях (см. рис. 6) можно заключить, что ограничение в виде задания второй производной существенно влияет на отклонение аппроксимирующей кривой (см. рис. 6, в) от аппроксимации без ограничений (см. рис. 4).

Выводы

В работе предложен математический подход к задаче полностью гладкого сопряжения кривых Безье, что позволяет в точке сопряжения сохранить непрерывность как самой функции, так и всех ее производных до порядка, равного степени заданных

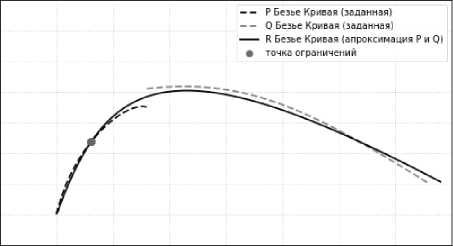
а)

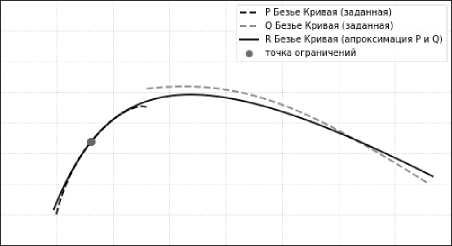
б)

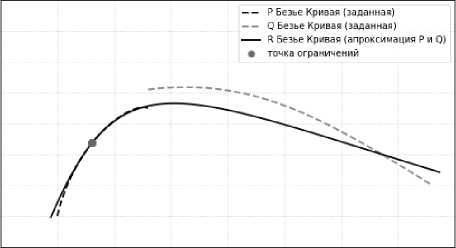
в)

Рис. 6. Сопряжение с ограничениями (интегральная норма), а – ограничение (29), б – ограничения (29-30), в – ограничения (29–31)

кривых Безье. Подход позволяет наложить на аппроксимирующую кривую дополнительные ограничения в виде прохождения через заданную точку и равенства производных в этой точке заданным значениям. Подход основан на формулировке экстремальной задачи при ограничениях в виде равенств, которая решается методом множителей Лагранжа и сводится к системе линейных алгебраических уравнений. В общем виде сформулированы дополнительные ограничения и приведен способ их включения в задачу сопряжения через дополнительные слагаемые функции Лагранжа. Кривые Безье и все ограничения записываются как частный случай В-сплайнов, для чего используется математический аппарат базисных функций В-сплайнов, что позволит в дальнейшем развить предлагаемый метод для задач сопряжений В-сплайнов и NURBS. Приводятся примеры аппроксимаций с учетом различных ограничений.