Аппроксимационная модель динамических жесткостных характеристик гидравлических виброизоляторов

Проблема снижения уровня вибраций, возникающих при работе различного оборудования, представляет достаточно актуальную задачу. Силовые установки, технологическое оборудование, транспортные системы являются источником широкого спектра колебательных процессов, оказывающих отрицательное воздействие на элементы машин, а также на операторов. Научные исследования в данном направлении продолжают проводиться, ведется поиск и разработка виброизолирующих элементов, а также методов расчета новых и оптимизации существующих конструкций систем виброизоляции.

Одним из перспективных направлений виброизоляции вибраций является применение в системах подрессоривания силовых установок гидравлических виброопор. В настоящее время в подавляющем большинстве систем подрессоривания силовых установок (вентиляторов, насосных станций, дизельгенерато-ров и т.п.) используются резинометаллические амортизаторы. Практический опыт их применения был обоснован простотой конструкции, что обусловило сравнительно низкую себестоимость изготовления. Однако их применение ограничивается узким спектром частот внешнего возмущения.

Применение гидравлических виброопор позволяет обеспечить эффективную виброизоляцию агрегата, который подвергается широкому

диапазону возмущающих частот. Конструкция опоры, выбранная жидкость и гидравлический механизм обеспечивают специфическое, широкополосное демпфирование. Конструкционные особенности гидравлических виброопор предопределяют их жесткостные и демпфирующие свойства, характер изменения которых имеет в большинстве случаев нелинейный вид и зависит от частоты и амплитуды внешнего воздействия. Эти факторы вносят влияние на динамическое поведение механической системы, что необходимо учитывать при расчете и проектировании систем виброизоляции. Так как жесткостные характеристики являются нелинейными, определенную трудность представляет их математическое описание.

В связи с этим, в настоящей работе рассматривается возможность моделирования динамической жесткости амортизационных опор на основе аппроксимирующих функций.

ПРЕДПОСЫЛКИ ИСПОЛЬЗОВАНИЯ ДИНАМИЧЕСКОЙ ЖЕСТКОСТИ

ПРИ ИССЛЕДОВАНИИ МЕХАНИЧЕСКИХ СИСТЕМ С ГИДРООПОРАМИ

Для примера рассмотрим широко используемые в настоящее время гидроопоры серии VL производства компании Simrit (или аналоги). Гидроопоры VL подходят для широкого спектра применения, например для крепления кабин и двигателей сельскохозяйственных и строительных машин, подъемно-транспортных средств, а также для крепления силовых установок и устройств со сложными процессами резонанса. Гидравлический механизм гидроопоры имеет характеристики жесткости и демпфирования, зависящие от частоты и амплитуды. Опорный элемент, в основном, предназначен для нагру- зок в осевом направлении, а также в радиальном, но может выдерживать небольшие карданные деформации. При небольших амплитудах возбуждения гидроопора имеет существенно меньшее демпфирование.

Работы многих авторов, посвященных изучению гидравлических опор, подтверждают актуальность и перспективность данного направления [1-3]. Большое внимание исследованию характеристик гидроопор посвящена работа Прониной Ю.О. [4; c. 47-51], где в качестве исследуемой была рассмотрена гидравлическая виброопора серии VL 03618704 (артикул 49028134). В работе приводятся результаты испытаний указанной опоры на вибростенде и получена амплитудно-частотная характеристика при гармоническом нагружении гидроопоры с закрепленной массой (рис. 1). В результате анализа полученных результатов эксперимента сделан вывод о возможности рассматривать гидроопору как одномассовый линейный элемент системы виброзащиты. Для проведения эксперимента использовались грузы массой 50 кг и 100 кг. При этом экспериментально выведенные значения коэффициентов жесткости и демпфирования виброопоры составляют соответственно K=0,7 кН/м и C=3,1 кН ^. с/м.

Полученные экспериментальным путем коэффициенты жесткости и демпфирования были в дальнейшем использованы в теоретических расчетах, и результаты показали хорошую сходимость.

При проектировании новых конструкций в расчет обычно берутся параметры жесткости, приводимые в справочниках. Причем, как правило, для упрощенных расчетов используют статические коэффициенты. Характеристики приведенной в качестве примера опоры VL 03618704 приведены в таблице 1.

На рисунке 2 приведены графики динамической жесткости в зависимости от амплитуды перемещений и частоты внешнего воздействия (рис. 2), которые имеют явный нелинейный характер.

В предварительном математическом моделировании можно использовать простейшую одномерную модель. Представим гидроопору с закрепленным грузом (M) как одномассовую механическую систему с одной степенью свободы, имеющую связь с неподвижным основанием через пружину (K) и демпфер (C) (рис.3).

Если внешнее возмущающее воздействие задано гармонической функцией, то приведенное уравнение установившихся колебаний, описывающее динамическое поведение системы, будет выражено следующим соотношением:

-v ■ 2/)х ■ с) л =Гш , (1)

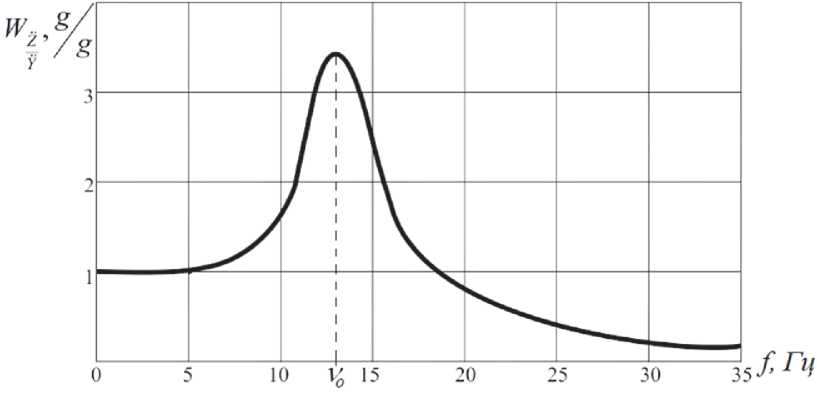
Рис. 1. Частотная передаточная функция гидравлической виброопоры VL (по Прониной Ю.О.)

Таблица 1. Справочные характеристики гидроопоры VL 03618704 (артикул 49028134)

Номинальные величины максимальных значений		Жесткость
Осевое давление		Радиальный сдвиг	Осевое давление
F z max	S z max	K x,y	K z
		S z =0	S z =5
[Н]	[мм]	[Н/мм]	[Н/мм]
6200	10	1050	600

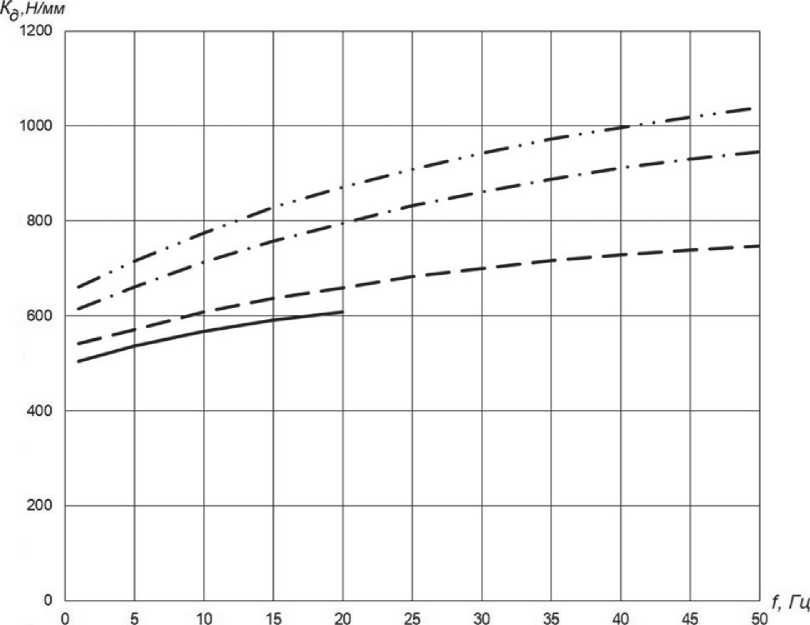
S = 5+0.1 мм; — ---s = 5±0.5 мм;

S = 5+2.0 mm; --S = 5+4.0 мм.

Рис. 2. Динамическая жесткость гидравлической гидроопоры

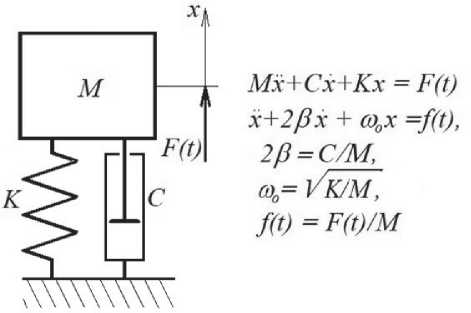
Рис. 3. Одномассовая система с параллельным соединением упругого и демпфирующего элемента

где  to0 = ^ KM - собственная циклическая частота системы,

β = 0,5⋅Χ/Μ - безразмерное относительное демпфирование.

Внешнее возмущающее воздействие задано функцией f(t) = F₀Cos(wt)/M , где to =2nv , v - частота внешнего возмущения,

F₀ – максимальная амплитуда внешнего воздействия. При этом амплитуда вынужденных колебаний вычисляется по формуле

A =

F 0

M ( го 0 - го² ) ² + 4р²®² "

При массе груза M=100 кг и коэффициенте жесткости гидроопоры K=0,7 кН/м значение собственная частоты колебаний юо = 83,666 рад/с или v о = 13,316 Гц, что подтверждается экспериментальной амплитудно-частотной характеристикой [1] (рис. 1). Если же при проектировочном расчете использовать справочное значение коэффициента жесткости для данной опоры K=0,6 кН/м (600 Н/мм), то значение собственной частоты колебаний составит юо = 77,46 рад/с (v о = 12,32 Гц), что отличается от экспериментальных данных. Предположительно, что такое расхождение в значениях собственных частот объясняется тем, что гидроопоры, обладая переменной жесткостью в зависимости от частоты внешнего воздействия, сдвигают частоту собственных колебаний системы в большую сторону. Следовательно можно сделать вывод о том, что при проектировании систем виброизоляции необходимо оперировать динамической жесткостью опор.

ВЫБОР АППРОКСИМИРУЮЩИХ ФУНКЦИЙ ДЛЯ МОДЕЛИРОВАНИЯ ДИНАМИЧЕСКИХ ЖЕСТКОСТНЫХ ХАРАКТЕРИСТИК

В связи с тем, что в большинстве случаев гидравлические виброопоры имеют нелинейные характер изменения жесткости, при проведении расчетов возникает необходимость замены их реальных характеристик математическими моделями на основе аппроксимирующих функций. В работе [5] рассматривается возможность использования аппроксимирующих функций при математическом моделировании подвески транспортных средств. Приведен сравнительный анализ различных методов аппроксимации рабочих характеристик упругих элементов. В работе [6] исследуются нелинейные жесткост-ные характеристики резинометаллических шарнирных соединений звеньев гусеничного движителя.

В настоящей работе так же предлагается аппроксимировать графики динамической жесткости, в качестве аргумента принимая частоту воздействия. Для рассматриваемой в качестве примера гидравлической опор VL (рис. 1) наиболее подходящими аппроксимирующими являются функции вида K = K₀ (a +b ■ ln( v +c)) , где K₀ – начальное (табличное) значение коэффициента жесткости. В результате проведенных расчетов методом наименьших квадратов [7] получены следующие коэффициенты, приведенные в таблице 2.

В дальнейшем полученные коэффициенты аппроксимации можно использовать при расчетах динамического поведения механических систем с амортизаторами, имеющими нелинейные характеристики. Для примера выбран режим, соответствующий наибольшей амплитуде внешнего воздействия. На рисунке приводятся графики частотной передаточной функции опоры, полученные экспериментальным [4] и расчетным путем с использованием только статического коэффициента жесткости и с параметрами динамической жесткости (рис. 4). Как видно из рисунка, использование динамической жесткости дает большее схождение с экспериментальными данными. Подставив аппроксимирующую функцию для вычисления значения коэффициента жесткости в выраже-

Таблица 2. Коэффициенты аппроксимации графиков динамической жесткости гидроопоры VL 03618704 (артикул 49028134)

s, мм a b c 5±0.1 -0,2780 0,4416 17,0653 5±0.5 -0,1621 0,4075 15,9493 5±2.0 0,3305 0,2553 12,4505 5±4.0 0,4252 0,2236 11,9234 ние (2), можно вывести зависимость для расчета собственной частоты системы:

а₀ = 2nv₀ = K₀ (a + b • ln( v₀ + c ) ) / M , M ( 2nv₀ ) ² / K₀ - a - b • ln( v₀ + c ) = 0 . (5)

Решая уравнение (5) методом последовательных приближений с точностью до 10^-3, получаем значение ν ₀ = 13,203 Гц, что сопоставимо с экспериментальными данными.

ЗАКЛЮЧЕНИЕ

В заключении можно сделать следующие выводы: предложенный подход с использованием при расчете систем виброизоляции функций, аппроксимирующих реальные нелинейные жесткостные характеристики, позволяет наиболее точно описать физические процессы работы ₅ гидравлических виброопор. Это позволяет уже ^. на этапе проектирования дать наиболее оптимальные результаты расчетов. Предложенный подход можно использовать для моделирования нелинейных жесткостных характеристик других типов гидравлических виброопор, имеющих бо- 6. лее сложный закон изменения в зависимости от частоты внешней нагрузки.