Аппроксимативные свойства слабо выпуклых множеств в пространствах с несимметричной полунормой

Хорошо известна, важная роль выпуклого анализа, при исследовании задач оптимизации и аппроксимации. В последнее время развивается параметрически выпуклый анализ, который в отличие от классического выпуклого анализа, рассматривает выпуклость не только как качественное понятие, но и путем введения характеристик сильной и слабой выпуклости придает этому понятию количественный характер. Анализ количественных характеристик (параметров) выпуклости приводит к более детальному исследованию задач и позволяет применять данные методы не только к выпуклым, но и к невыпуклым (слабо выпуклым) объектам. Исследованию различных классов сильно и слабо выпуклых множеств посвящены работы [1], [2], [5], [7] - [9], в которых сильная и слабая выпуклость множества, определяется через норму банахова пространства. В работе [3] показано, что методы параметрически выпуклого анализа, можно развить и для так называемой несимметричной нормы, при этом роль шара, играет несимметричный квазишар. В настоящей работе мы отказываемся не только от симметричности, но и от ограниченности квазишара, что позволяет применять развиваемые здесь методы к надграфикам функций, которые являются неограниченными множествами. Здесь под квазишаром понимается выпуклое замкнутое множество, для которого ноль является внутренней точкой. Функция Минковского такого квазишара представляет собой несимметричную полунорму и используется в определениях опорных условий сильной и слабой выпуклости.

2.    Определения и обозначения

Пусть Е - банахово пространство. Через int X, ЭХ и X будем обозначать соответственно внутренность, границу и замыкание множества X С Е. Значения функционала р Е Е * на векторе ж Е Е будем об означать (р, ж).

Определение 2.1. Суммой Минковского множеств X С Е и У С Е называется множество

X + У = {ж + у | ж Е X, у Е У } .

Определение 2.2. Диаметром множества X С Е называется величина diam X = sup ||ж — уЦ.

х<у^Х

Определение 2.3. Шаром радиуса d >  0 с центром в точке а Е Е называется множество

Вд(а') = {ж Е Е : ||ж — а| 6 d}.

Определение 2.4. Квазишаром М в банаховом пространстве Е называется выпуклое замкнутое множество М С Е, для которого 0 Е int М .

Заметим, что квазишар М является шаром относительно некоторой нормы, эквивалентной исходной норме пространства Е, тогда и только тогда, когда он ограничен относительно исходной нормы Е и симметричен, т.е. —М = М .

Определение 2.5. Функцией Минковского квазишара М называется функция Цм : Е ^ [0; +то) такая, что

Цм (ж) = inf {t > 0| ж Е ІМ }    V ж Е Е.

Определение 2.6. Функция р : Е ^ R называется несимметричной полунормой, если она полоэюителъно однородна;

р(Аж) = Ар(ж)    V ж Е Е V А > 0

и субаддитивна;

р(ж + у) 6 р(ж) + р(у)    V ж, у Е Е.

Замечание 2.1. Известно, что функция ц : Е ^ [0, +то) является несимметричной полунормой тогда и только тогда, когда она является функцией Минковского некоторого квазишара.

Определение 2.7. Пусть М С Е - квазишар. М-расстоянием от множества X С Е до множества У С Е называется величина ум(Х,У) =   inf   Мм(ж — У).

хех, ^еУ

В частности, М-расстояние от точки ж Е Е до множества У С Е определяется формулой ем (ж, У) = inf Цм (ж — у).

уеУ

Замечание 2.2. Непосредственно из определений следует, что ум (ж, У) = inf {t > 0| ж Е У + ІМ} = inf {t > 0| У Q(t — ІМ) = 0^ .

Определение 2.8. Пусть М С Е - квазишар. М-проекцией точки ж Е Е на множество У С Е называется множество

Рм (ж, У) = У р|(ж — ем (ж, У )М).

Также при е >  0 опреледим е-М-проекцию точки ж Е Е на множество У С Е;

р м (ж, у ) = У Р^ж — (ем (ж, У) + е)М ).

Определение 2.9. Будем говорить, что множество X С Е удовлетворяет опорному условию сильной выпуклости относительно квазишара М С Е, если

X — ж СМ-- ^У, * V у ЕЕ \ X Vж ЕРм (У,Х ). ем (у,х )

Определение 2.10. Будем говорить, что множество У С Е удовлетворяет опорному условию слабой выпуклости относительно квазишара М С Е, если

У Р (у + ^ж— VА — intм) = 0 ем (ж, у )         /

V ж ЕЕ \У V у ЕРм (ж,У ).

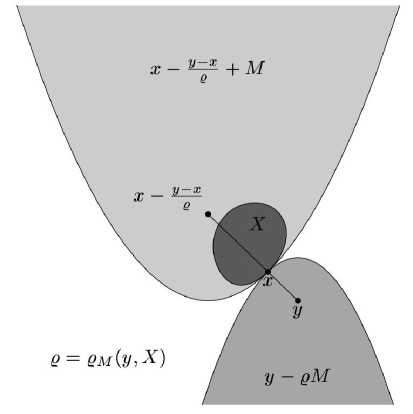
Рис. 1. Опорное условие сильной выпуклости

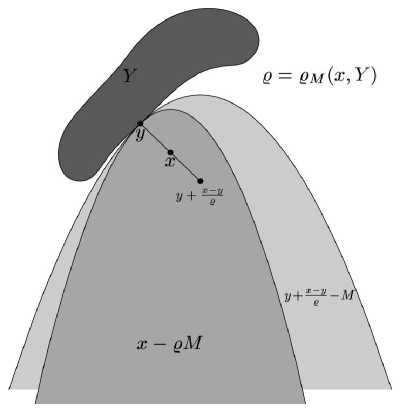
Рис. 2. Опорное условие слабой выпуклости

Замечание 2.3. Если ж Е Е \ У, у Е Рм (ж, У), то 0 = ж — у Е дм (ж, У )М и, следовательно, дм (ж, У) > 0. Таким образом, в определениях 2.9 и 2.10 знаменатели не обращаются в ноль.

Определение 2.11. Множество X С Е называется параболичным, если для любого вектора b Е Е множество (b + 2X) \ X ограничено.

Определение 2.12. Множество X С Е называется ограниченно равномерно выпуклым, если

5^(е) > 0 V d> 0 V е > 0, где

51 (е) = sup ^5 Е (0, Е] | В₅ ж^ ) С X

V ж, у ЕX ПВД0) :

IIх

— -I >  еР

3.    Вспомогательные результаты

Лемма 3.1. Пусти М С Е - квазишар, У С Е. Тогда

• (г) дм (жі,У) — дм (ж2,У) 6 Дм(жі — ж2) V жі,ж2 Е Е;

• (и) для любого вектора ж Е Е такого, что дм (ж, У) > 0, справедливо соотношение

ж Е У + дм (ж, У ) int М.

Если дополнительно для числа ст >  0 выполнено включение В„ (0) С М (такое ст существует. т.к. 0 Е int М). то

(ггг) функция дм С,У) удовлетворяет условию Липшие,а на Е с коисигаптой ^ и

• (Л) для любых полоэюителъных чисел е-д е₂ и векторов ж_і,ж₂ Е Е таких, что ||жі — ж₂|| 6 сте₂- справедливо включение Рм (ж_і,У) С Рм^+2е2(ж₂,У)•

Доказательство. Утверждение (г) следует из определения М-расстояния и субаддитивности функции Минковского. Если В_ст (0) С М, то дм (ж) 6 у для любого вектора ж Е Е.

Докажем утверждение (гг). Предположим противное: существует точка ж Е (ж — дм (ж, У) int М ) П У. Тогда уту—уу Е int М. Следовательно, существует число t Е (0, д_м(ж, У )) такое. что ^^ Е М. Поэтому ж Е У + 1М и д_м(ж, У ) 6 t < д_м(ж, У ). Противоречие.

Применяя утверждение (г), получаем утверждение (ггг).

Докажем утверждение (гн). Так как ±(ж2 — жі) Е Е2В_СТ (0) С Е2М, то справедливо нера-веік-тво тах{дм(ж₂ — ж1),дм(жі — ж₂)} 6 е₂. Отсюда, іі ітз утверждения (г) следует, что

0м ($1,У) 6 0м ($2, У) + е₂. Поэтому для любого вектора у Е Р^ ($1,У) справедливы неравенства цм($2 — у) 6 £2 + Цм($1 — у) 6 £2 + 0м (^1, У) + £1 6 0м($2, У ) + £1 + 2е2- Следовательно. у Е Рм^+е"2($2 , У)•

□

Лемма 3.2. Любое замкнутое выпуклое мноэюество У С Е удовлетворяет опорному условию слабой выпуклости относительно любого квазишара М С Е.

Доказательство. Пусть заданы точки $о Е Е \ У и уо Е Рм($о,У )• Обозначим 0о = 0м($о,У )• го = ^X0-S0. Так как уо Е Рм($о,У )• то $о - уо Е 0оМ. т.е. го Е М. Согласно лемме 3.1 ( гг) имеем $о Е У + 0о int М. Следовательно, У П ($о — 0о int М ) = 0. В силу теоремы об отделимости существует функционал р Е Е* такой, что

(р, у) < (р, $о) — 0о (р, г)    V у ЕУ V г Е int М.

Следовательно,

(р, у) 6 (р, $о) — 0о(р, го) = (р, уо)     V у Е У,( 2)

(р, уо) < (р, $о) — 0о(р, г)     V г Е int М, то есть

(р, г) < (р, го)     V г Е int М.(3)

Складывая неравенства (2) и (3), получаем

(р, у + г) < (р, уо + го)     V у ЕУ V г Е int М.

Поэтому уо + го Е У + int М. а. 'значит. У Q (уо + ^“—м) - int М^ = 0. Используя определение 2.10, получаем требуемое утверждение.□

Для любого множества У С Е определим

7м(У) = sup 0м($,У), х Е Е

8м (У) = {$ ЕЕ : 0 <  0м ($, У ) <  7м (У)},

Тм (У) = {$ Е Е : множество Рм ($, У) одноэшзмеитио}.

В работе [4] рассматривается более сильное условие параболичности. Однако доказательство теоремы 1.2 работы [4] остается справедливым, если условие параболичности понимать в смысле определения 2.11. Таким образом, справедливо следующее предложение.

Предложение 3.1. Пусть в банаховом пространстве Е квазишар М параболичен и ограниченно равномерно выпукл, множество У С Е замкнуто. Тогда множество Тм (У) всюду плотно в 8_м(У ). т.е. 8_м(У ) С Тм(У ).

Лемма 3.3. Пусти в банаховом пространстве Е квазишар М параболичен и ограниченно равномерно выпукл. Пусти мноэюество У С Е замкнуто и удовлетворяет опорному условию слабой выпуклости относительно квазишара ПМ. Пусти 7м (У) > 0. Тогда 7 м (У ) >  R-

Доказательство. Так как sup 0м($, У) = 7м(У) > 0, то найдется точка $о Е Е такая, хЕЕ что 0м($о, У) > 0. Зафиксируем точку уо Е У. Тогда 0м(уо,У) = 0. Поскольку согласно лемме 3.1 (ггг) функция 0м (•, У) непрерывна, то на отрезке [$о,уо] найдете я тонка $1 такая, что 0 = 0м(уо,У) < 0м($1,У) < 0м($о,У) 6 7м(У)■ Следовательно. $1 Е 8м(У)■ Согласно предложению 3.1 и в силу замкнутости У существует точка $ Е Тм(У) \ У-Следовательно, найдется у Е Рм($, У)• Обозначая b = у+R^—у), в силу определения 2.10 имеем УП(b — Rint М) = 0. Следов;етелыю. 0м(Ь,У) > R. Пштому 7м(У) > 0м(Ь,У) > R. □

Далее нам понадобится следующий аналог леммы 2.1 работы [4], доказательство которого аналогично доказательству леммы 2.1 из [4].

Предложение 3.2. Пусть множество М С Е выпукло и параболично, пусть 0 < Хі <  Х₂. ж_і,ж₂ С Е. Тогда міюжество (Х_іМ + ж_і) \ (Х2М + ж₂) ограничено.

Лемма 3.4. Пусти квазишар М С Е, векторы ж, у Е Е и число d > 0 удовлетворяют неравенствам 0 < ||ж|| 6 d • Им (ж), 0 < ||у|| 6 d • Им (у) Тогда min{им (ж), Им (у)}

d

• ⁵м (

ж

-

У

Им (ж)    Им (у)

^ 6 Им (ж) + Им (у)

^{— И}м^{(ж + у)},    (4)

где величина 5м(•) определена формулой (1)

*

Доказательство. Обозначим ж             у а   Им (ж)’          Им (у)’

а + b с =  2,     5 = 5м(|а

— b|).

Так как а,Ь Е М П ВД0), то |с| 6 d. Используя равенство (1), шю Bg (с) С М. Поэтому с (1 + ^) Е М и. следовательно. Им (с)

5 = 5м (|а — b|) 6 " ° 2 ^Ь^ 6 d, то справедливо неравенство

получаем включе-

6 у^у • ПОСКОЛЬКУ

^{Им (с) 6 1} - V

Обозначим Иі = Им (ж). И2 = Им (у) Без потери общности можно считать, что И2 6 Иі- Далее используем выпуклость и положительную однородность функции Им и учитываем, что Им (а) = 1:

Им (ж+ у) = им ((Иі — И2)а+И2(а+b)) 6 (Иі —И2) • Им (а)+И2 •Им (а+b) = Иі — И2 +²И2 • Им (с).

Используя оценку (5), получаем

Им (ж + у) 6 Иі + И2 — ^И2⁵ = Иі + И2 — d min{иi, И2}.

Лемма 3.5. Пусти в банаховом пространстве Е заданы ограниченно равномерно выпуклый квазишар М и ограпачеппые последовательности {жк}• {ук } такие, что

lim sup Им (жк) 6 Иі, к^ж

lim sup Им (ук) 6 И2, к^ж

lim inf и м (жк + ук ) >  Иі + И2, кшж

где Иі > 0 и И2 > 0. Тогда lim к^ж

жк

Иі

-

ук

И2

= 0.

Доказательство. Поскольку в силу субаддитивности функции Минковского

Им (жк + ук) 6 Им (жк)+ Им (ук)    Vk Е N, то в силу условий леммы получаем, что существуют следующие пределы:

lim и м (жк ) = И1,     lim Им(ук ) = И2, lim Им(жк + ук) = Иі + И2•

к^ж             к^ж             к^ж

Без потери общности будем считать, что Им(жк) > ^Д Им(Ук) > ^2 Для любых к Е N. Тогда в силу ограниченности последовательностей {жк} и {ук} выражение d-8^ max! Іжк| _Щ_ 1 d* SUp XXXdj^x \       / \ ,       / \ I кем       Им (жк) Им (ук)

конечно. Применяя лемму 3.4, получаем, что min{Mi,M2}

2d

• ^м (

Xk Ук

Мм (хк )    мм (Ук )

6 ^Мм ^(хк ) ^{+ М}м ^(ук ) ^{— М}м ^(хк ^{+ у}к) ^м О

(к м то).

Отсюда в силу ограниченной равномерной выпуклости множества М имеем lim к^^

Хк Ук Мм ^(хк )    Мм ⁽Ук )

= 0.

Используя ограниченность последовательностей {хк}, {ук} и соотношения (6), получаем требуемое утверждение.

□

4.    Основные результаты

Теорема 4.1. (О диаметре е-проекции). Пусть в банаховом пространстве Е квазишар М параболичсн и ограниченно равномерно выпукл. Пусть множество У С Е замкнуто и удовлетворяет опорному условию слабой выпуклости относительно квазишара КМ. Пусть заданы число г Е (0, К). век тор b Е Е. послсдоватслыгость векторов {хк } С b — гМ такая, что lim рм(хк , У) = ро Е (0,К — г), и бесконечно малая последовательность 'к >^

положительных чисел {ек}• Тогда lim diam Р^ (хк,У) = 0.

к^^

Доказательство. Обозначим

• ео = ¹ min{рo, К — г — ро}.

  
  

Без потери общности будем считать, что ек 6 ео,     |рм(хк,У) — Qo| 6 ео V к Е N.

В силу леммы 3.3 справедливо неравенство К 6 7м(У)• Тогда для любого к Е N справедливы неравенства 0 < Qo — ео 6 рм(хк , У) 6 Qo + ео < К 6 7м(У), а значит, и включения хк Е 8м (У)• Поскольку М - квазишар. то существует число ст > 0 такое, что В_ст (0) С М. Поэтому согласно предложению 3.1 для любого к Е N существует вектор Хк Е В_ст£к(хк ) О Тм (У)• Из пункта (ггг) леммы 3.1 следуют неравенства

|рм(хк,У) — рм(хк,У)| 6 ек    Vk Е N,(8)

а из пункта (гг) этой же леммы получаем включения рм (хк ,У) С^ (хк ,Y) Vk Е N.(9)

В силу включений (9) для завершения доказательства достаточно показать, что lim diam РМ (хк ,У) = 0.(10)

кгого

Так как К — ео < К 6 7м (У)• то найдетня вектор Ь1 Е Е такой, что К — ео <  рм(Ь1,У )• Согласно лемме 3.1 (гг) имеем Ь1 Е У + Рм(Ь1,У ) int М. Поэтому Ь1 Е У + (К — ео)М, а значит,

У СЕ \ (bi — (К — ео)М).                            (11)

Если у Е Рм(хк,У), то у Е хк —

(Рм(хк,У ) + 3ек^М с Хк — (ро + 5ек^М с хк — (ро + 6ек^М с b — (г + ро + 6ео^М.

Поэтому согласно включению (11) имеем

^Рмі^{к (г}к, ^Y ) ^С ^5 ^— (^{г + д}о ^{+ 6в}0^М ) \ ^51 ^{— (R —} Ео)М ) .

Поскольку из равенства (7) следует неравенство г + до +6во <  R -во, то в силу предложения

• 3.2 получаем неравенство

  sup sup     | у | < +^.

  
  

^keN у^^рм^к(^zk;у )

Так как дм(гк,Y) < до + Зво, то гк е Y + (до + 3ео)М. Отсюда и из включения (11) следует, что гк е ^bi - (R - до - 3во)М^. Таким образом, учитывая включения гк е хк - воМ С b - (г + во)М, получаем гк е (ь - (г + Ео)М) \ (51 - (R - до - Збо)М^ ■

Учитывая неравенство г + во <  R - до - Зво ^{и е}Щ^е Р^аз применяя предложение 3.2, получаем неравенство

sup ^гк || < +^. keN

Так как гк е Тм(Y ) то для любого к е N существует точка. Ук е Рм(гк,Y )■ В силу определения 2.10 имеем

(а_к -R int М ) AY = 0 V к е N,

где

-к = Ук +

гк

-

Ук

= Ук + R

Zk

-

Ук

Ум (гк - Ук ) ‘

УRM ^(гк - Ук )

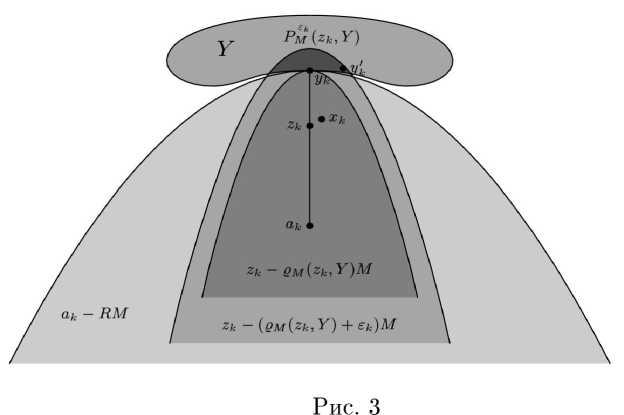
Зафиксируем произвольную по-

следовательность что

Ук е РЦ¹ (гк,Y )

Поскольку Ук е

Ум (гк

-

У к )

{Ук } такую,

V к е N.

(16) Рм (гк,Y ) то дм (гк ,Y) и,

учитывая соотношения (8) и lim д_м (х_к ,Y ) = д_о, получаем кюго

lim ум(гк - Ук) = до.   (1Д кюго

Из соотношения (14) следует, что дм (-к ,Y ) >  R- Поэтому

Ум (ак - Ук) > R V к е N.

Используя соотношения (8), (16), получаем

limsupум (гк - Ук) 6 lim дм(гк,Y ) кюго                ^кюго

= до ■

Поскольку согласно соотношению (15) справедливы равенства ум (-к-гк ) = R-Ум (гк—Ук ) то в силу (17) имеем

lim ум (-к - гк ) = R кюго

-

до ■

Из соотношений (12), (13), (15), (16), (17) получаем ограниченность последовательностей {zk}, {yk} {yk} и {-k}• Отсюда и из соотношений (18) - (20) в силу леммы 3.5 приходим к равенству

Т    ak — z k zk — у'к lim —---k k^^ II R — 80      80

Так как в силу (15) справедливы равенства

«к —к R-Вм ^(zk ^-ук )

= 0.

^zk -у к Ум бк—Ук )

то согласно соотноше

нию (17) имеем lim || д-^ — Zkegk Ц = 0. Отсюда и из равенства (21) следует соотношение lim \\yk — ykII = 0, k^^

которое в силу произвольности последовательности {yk}, удовлетворяющей соотношению (16), дает требуемое равенство (10).                                                    □

Теорема 4.2 (о чебышевском слое). Пустъ в банаховом пространстве Е квазишар М параболичсп и ограпичсппо равномерно выпукл. Пусть множество У С Е замкнуто и удовлетворяет опорному условию слабой выпуклости относительно квазишара RM. Пустъ задана точка ж Е Е такая, что 0 <  8м (ж, У) <  R. Тогда множество Рм (ж, У) одноэлементно.

Доказательство. Фиксируем последовательность положительных чисел {Ek }, монотонно сходящуюся к нулю. В силу теоремы 4.1 справедливо соотношение diam РМ (ж, У) ^ 0 при к ^ то. Отсюда из замкнутости и вложенности множеств РМ (ж, У) получаем, что множество Q РМ (ж, У) одноэлементно. Замечая, что keN

Рм(ж, У) = Р| РМ(ж, У), получаем доказываемое утверждение.                      □ keN

Замечание 4.1. В условиях теоремы 4.2 множество {ж Е Е| 0 <  8м (ж, У) < R} называется чебышевским слоем множества У. Таким образом, теорема 4 утверждает, что для точек чебышевского слоя существует единственная М-проекция.

Теорема 4.3 (о ближайших точках). Пустъ в банаховом пространстве Е квазишар М параболичсп и ограпичсппо равномерно выпукл. Пусть мпоэіссство X С Е выпукло, замкнуто и удовлетворяет опорному условию сильной выпуклости относительно квазишара —гМ, а множество У С Е замкнуто и удовлетворяет опорному условию слабой выпуклости относительно квазишара RM, г де 0 < г < R. Пустъ 0 <  8м (X, У) < R — г. Тогда min рм (ж — у) достигается в единственной паре точек.

хЕХ, уЕУ

Доказательство. Обозначим 8о = 8м (X, У ), Ео = 2(R — г — 8о) • По определению 2.8 существуют последовательности {yk } С У и {жk} С X, такие, что

lim рм(жk — yk ) = 80. k^^

Обозначим Ek = рм(жk — yk ) — 8о- Без потери обтщюсти будем считать, что Ek 6 Eo для любого к Е N. В силу теоремы 4.2 и леммы 3.2 для любого индекса, к Е N найдутся тонки yk Е Р_м(ж_k , У) л ж ) Е Р-м(y_k,X ). Для л тобого к Е N обозначим

‘            R                  ‘                   ‘             г‘

• 6‘ = y‘ + рм(Ik — yk)    — y‘)’ С‘ = ж‘ + рм(жk — yk)    —

Из определений 2.9, 2.10 и равенства р-м(yk — ж) ) = рм (ж) — yk ) следует, что для любого к Е N

У П (bk — R int М) = 0,(24)

X С —гМ + ck.(25)

Следовательно,

—yk ЕЕ \ (R int М — bi),

— ж ₎ Е гМ — c1    V к Е N.

Поскольку цм(жк - Ук ) = 80 + Ек 6 80 + Е0, тО жк - Ук Е (80 + Е0)М для любого к Е N. Отсюда и из соотношений (24) - (26) получаем

-Жк Е (тМ - С1) \ ((R - 80 — Е0 ) int М - ф)    V к Е N,             (27)

-Ук Е ((т + 80 + Е0)М - С1) \ (R int М - 61)     V к Е N.             (28)

Учитывая неравенство т + 80 + Е0 < R, в силу предложения 3.2 получаем ограниченность последовательностей {жк} и {ук }.

Поскольку цм(жк - Ук ) = 80 + Ек 6 8м(жк,Y ) + Ек, то ук Е РМ(жк,Y )• Отсюда и из включений ук Е Рм (жк ,Y ) С РМ (жк ,Y ) следует, что

^Ук - Ук II 6 diam рм (жк ,Y )    V к Е N.

Поэтому согласно соотношению (27) и теореме 4.1 получаем, что lim ||Ук - Ук|| = 0.                                          (29)

к К^

Используя неравенства цм(жк - Ук ) 6 8м(-Ук, -X ) + Ек, получаем включения {-жк , -жк } С Рм (-Ук, -X ). В силу леммы 3.2 множество - X удовлетворяет опорному условию слабой выпуклости относительно квазишара RM. Поэтому согласно соотношению (28) и теореме 4.1 получаем, что

lim ||жк - жк || = 0. к^^

Для любого к Е N обозначим

r

Ьк = Ук +--(жк - Ук ),

т ,             х

Ск = жк +--(жк - Ук ).

Из соотношений (22), (23), (29) - (31) с учетом ограниченности последовательностей {жк } и {Ук } следует, что

lim ІЬк - Ьк || = 0, к^^

Из соотношений (24), (25) имеем

lim ||ск - Ск|| = 0. к^^

Цм ^(Ьк ^- Уп) > ^R

V к,п Е N,

цм(ск -ж„) 6 т

V к, п Е N.

Отсюда, учитывая липшицевость функции Минковского и соотношения (32), получаем

liminf цм (Ьк -УпА > R, к—— ^       \         / п——^

lim sup цм (Ск - ж„) 6 т.

к ——^ п —^

Следовательно, в силу субаддитивности функции Минковского имеем

liminf цм (bk - Ск - Уп + ж„ ) > R -к——^       \                     / п—^

т.

Для любого к Е N обозначим /к = жк - Ук, 9к = Ьк - Ск- Тогда из равенств (31) получаем 5к = R-g-e0/к- Из соотношений (22) и (35) следует, что lim цм(/к) = 80,     lim цм(9к) = R - т -80,    liminf цм(дк + /п) >R - т.

к^^              к^^                     к—^

п ——^

Кроме того, последовательности {fk} и {9n} ограничены. Отсюда в силу леммы 3.5 получаем равенство lim Д^ —         = 0, то есть lim Iff — fn| = 0. Следовательно, последова- k—^ -0 ^ ' -0

n—— ^n—— ^

тслыюсть {fk } фундаментальна. а значит, сходится к некоторому вектору fo Е Е. причем цм ^(fo ) = 9o-

Для любых k,n Е N обозначим hkn = bk — ck — yn + xn, ekn = ck — xn. Тогда hkn = 9k + fn =--------—fk — fn ^-----fo    (k,n ^ то).(36)

9o9o

Используя соотношения (33), (34), получаем lim цм(hkn) = R — r, k——^

n——^

lim sup цм(ekn) 6 r, k——^ n——^

lim inf цм (hkn + ekn) >  R.

k ——^ n——^

Еще раз применяя лемму 3.5, приходим к соотношению lim || -^^ — ^у ||  = 0.

n—^

Используя соотношение (36) и сходимость fk ^ fo при k ^ то, получаем соотношение lim ||^ — ^Ц = 0. Поскольку -^ — ^Г = ^x" фл. то доказано соот-n—^

ношение lim ||xk — x_n^ = 0, которое означает фундаментальность последовательно-k——^ n——^

сти {xk}■ Следовательно, последовательность {xk} сходится к некоторому xo Е Е. Поэтому yk = Xk — fk ^ yo при k ^ то. г,ле yo = xo — fo- Так как множе ства X и У замкнуты, то xo Е X, yo Е У. Используя соотношение (22), получаем Цм(xo — yo) = 9o = 9м(X, У) = inf цм(x — y). то минимум min цм(x — у) доетн-xEX, yEY                              xEX, yEY гается на паре точек (xo, yo). Предположим, что минимум min цм(x — у) достигается xEX, yEY также на паре точек (x^, y^)• Рассмотрим последовательности x'k = I

xo, k четно, xo, k нечетно,

yb = {

yo, k четно, yo, k нечетно.

Так как в силу доказанного последовательности {x_k } и {yk } сходятся, то xo = xo, yo = yo-

Тем самым доказана, единственность.

□

Работа, выполнена, при поддержке РФФИ, грант 10-01-00139 и ФЦП «Научные и научнопедагогические кадры инновационной России».