Априорное определение тягового сопротивления глубокорыхлителя методами теории размерностей и подобия

Функционирование машин для глубокого рыхления протекает в условиях изменяющихся внешних воздействий, обусловленных различными факторами, к которым относятся физико-механические свойства почвы. Внешние воздействия в сочетании с выбранными режимами работы и параметрами машин влияют на качественные и энергетические показатели технологического процесса глубокой обработки почвы. Существенной особенностью большинства факторов, определяющих показатели процесса, является то, что они могут быть отнесены к случайным факторам, значения и характер изменения которых могут быть установлены лишь в результате экспериментальных исследований. Сам процесс функционирования машин для глубокой обработки почвы также является случайным, описываемым статическими закономерностями. При этом качественные и энергетические показатели технологического процесса для подобных машин явля ются определёнными.

Такая интерпретация процесса функционирования машин для глубокого рыхления позволяет использовать для выражения связей между их параметрами, режимами работы и физико-механическими свойствами почвы теорию подобия. С помощью информационно-статистического моделирования [1] и теории подобия [2] можно по результатам ранее проведённых измерений исследуемых переменных определить функцию, которая раскрывала бы связи между ними.

Таким образом можно решить следующие задачи:

• •    определить тяговое сопротивление глубокорыхлителей в зависимости от физико-механических свойств почвы, параметров и режимов работы;

• •    определить параметры глубокорыхлителей в зависимости от заданного тягового сопротивления в соответ-

• ствии с тяговым классом агрегати-рующего трактора при различных состояниях почвы и осуществить выбор режимов работы.

Тяговое сопротивление глубокорых-лителей при заданных режимах работы можно достаточно точно определить и методом динамометрирования. Однако применение этого метода ограничено конкретными условиями испытаний. Чтобы обеспечить достоверность измеренного тягового сопротивления ряда различных глубоко-рыхлителей, необходимо создать однообразные почвенные условия, т.е. бесконечно большое число опытов необходимо провести в ограниченные сроки.

Если однообразие почвенных условий не удаётся обеспечить, необходимо вводить поправочный коэффициент, точно определить который не представляется возможным. С помощью теории подобия можно определить зависимость, связывающую тяговое сопротивление глубокорых-лителей с физико-механическими свойствами почвы, с параметрами и режимами работы. Таким образом, поправочный ко-эффи циент, уч итывающи й ф изико-меха-нические свойства почвы, будет уже включён в зависимость и можно будет определить тяговое сопротивление глубокорых-лителей в различных условиях, при этом значительно сократив объём экспериментальных исследований.

Известно, что у подобных процессов можно определить некоторые сочетания параметров, подобные для различных машин и не имеющие размерности, называемые критериями подобия.

Известны два основных способа определения критериев подобия [2] при взаимодействии рабочего органа с почвой:

• •    на основании размерностей величин, определяющих протекание технологического процесса;

• •    на основании анализа системы уравнений, описывающих процесс обработки почвы и приведение их к безразмерному виду.

Анализ размерностей позволяет определить критерии подобия без знания математической зависимости между физи ческими величинами изучаемого процесса. Сущность его сводится к следующему [2]:

• —    составляется перечень параметров, определяющих процесс;

• -    устанавливаются формулы размерностей каждого из параметров;

• -    заменяются в формулах основные единицы измерения соответствующими физическими величинами;

• —    выполняются преобразования и определяются искомые критерии подобия.

Тяговое сопротивление почвообрабатывающих машин Рт можно представить функциональной зависимостью [3, 4]:

Рт = f (а,В,и,Н,д),       (1)

где CL - глубина обработки, м;

В - ширина захвата машины, м;

• V    - скорость агрегата, м/с;

Н — твёрдость почвы, Па;

д ускорение свободного падения (земного притяжения), м/с^.

Параметры формулы (1) будут являться показателями, определяющими процесс разрушения пласта почвы.

Твёрдость обрабатываемого слоя Н является параметром физико-механических свойств почвы, представленным в протоколах машин на МИС.

При обработке почвы возникает перемещение масс (машины и почвы), поэтому необходимо учитывать ускорение земного притяжения д.

Представим размерность каждой величины, входящей в формулу (1), в виде произведения степенных функций длины L, времени Т и силы F:

[Рт] = L°-T°-F1

• а] = L1 ■ Т° ■ F°

В]    =L1-T°-F°         (2)

V] = L1 • Т"1 • F°

Н] = Г2 -Т0-Ғ1

у] = L1 ■ Т"2 ■ Ғ0.

Значения показателей степеней при основаниях L, Т и Ғ размерного ряда рассматриваемой функции (1) для каждого из входящих в неё параметров образуют размер- ную матрицу, представленную в таблице 1.

Таблица I

Размерная матрица параметров функции Р_т =/(и, В, V, Н, д)

Размерность	Параметры
	рт	а	В	V	н	д
Длина L	0	1	1	1	-2	1
Время Т	0	0	0	-1	0	-2
Сила F	1	0	0	0	I	0

Ранг матрицы равен 3 (А=3), т.к. определитель, составленный, например, из трёх последних столбцов, не равен нулю [5].

1-2  1

Д= -1   0   -2 = 1 ■ 0 ■ 0 - 1 • 1 ■ (-2) + (-2) • (-2) • 0 - (-2) ■ 0 • (-1) + 1 • (-1) ■ 1 - 1 • 0 • 0 * 0.

0 1 о

Согласно методике, описанной ранее, необходимо перейти к безразмерной форме записи функции (1) для определения критериев подобия 71 .

Число критериев подобия определяется по формуле

A = Z7-A, (3) где П - число переменных в формуле (1); А = 3 - ранг размерной матрицы.

Следовательно, N = 3.

Чтобы определить каждый из трёх критериев подобия 71^,712,^3, необходимо из числа параметров, входящих в формулу

(1), выбрать основные, которые в размерной матрице образуют отличный от нуля определитель и оказывают наибольшее влияние на качественные показатели технологического процесса обработки почвы. Этим условиям отвечают параметры: глубина И, скорость V и твёрдость Н.

Критерии подобия формируют как произведение основных параметров (Я, V, Н) в соответствующих степенях на один из оставшихся среди рассматриваемых (формула (I)), степенью которого задаются [4].

= Рт ■ а“ ■ ■ Н8. (4)

[лД = (F1 ■ Т° ■ L0) ■ (Г° ■ Т° ■ L1)" ■ (Р° ■ Т"1 ■ L1)!3 ■ (Г1 ■ Т° ■ L"2)8 = _ pl+S , ^а+р—25 , р—р

Чтобы величина 711 была безразмерной, необходимо показатели степеней при основаниях размерного ряда в уравнении размерностей (5) приравнять к нулю:

1 + 5 = 0 1+£-25 = 0 .    — д = о .

Отсюда и = —2; ^ = 0; 5 = —1. Подставляя в формулу (4), получим

Аналогичным образом формируем критерий подобия ТІ2:

тг2 = д ■ а“ ■ у^ ■ Н5.       (8)

[я2] = (F0 ■ Т"2 ■ L1) • (F0 • Т° • Ц)“ ■ (Р° ■ Т"1 ■ ЬТУ ■ (F1 • Т° • Г2)8 = _ pl+a+p—25 ,   2 —р , р5

1 + сс + р — 25 — 0' -2-/? = о :

5 = 0

а = 1; р = -2; 5 = О

Обратная величина полученного критерия (11) называется критерием механического подобия Фруда.

Представим в безразмерной форме критерий ТГд:

л3 = В ■ аа ■ т>Р ■ Н5.    (12)

[тт3] = (Ғ0 ■ Т° ■ L') ■ (Ғ0 ■ Т° ■ Ц)“ ■ (Р° ■ Т"1 ■ Г/ ■ (Ғ1 ■ Т° ■ Ь"2У = _ pl+a+p—28 , р—р . р8

Приравняв к нулю показатели степеней в уравнении размерностей (13), полу чим:

1 + сг + ^ — 25 = 0'

-Р = о

5 = 0

а = —1; р = 0; 5 = 0

в

Отсюда 7ГЧ = — .

а

В соответствии с 7Г-теоремой (второй теоремой подобия) формула (1) может быть представлена в виде функциональной зависимости критериев [2]:

Пг = Г(Л2,ЛзУ (16)

Подставляя формулы (7), (11), (15) в зависимость (16), получим:

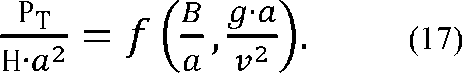
С помощью полученной зависимости (17) можно решить поставленные в работе задачи по определению тягового сопротивления почвообрабатывающих машин.

В качестве исходных данных для решения поставленных задач использовались протоколы Сев.-Кав. МПС приемочных и периодических испытаний машин для глубокой обработки почвы за период с 1984 по 2006 гг.

К ним относятся:

• •    глубокорыхлитель навесной ГРН-3 [6];

• •    плуг-глубокорыхлитель чизельный навесной ПЧН-4,0 [7];

• •    орудие основной обработки ПЧС-10-40 [8];

• •    глубокорыхлитель со сменными рабочими органами типа «пара-плау» ПУН-08 [9];

• •    комбинированный агрегат основной обработки почвы КАО-10-3 5 [10];

• •    универсальная несущая система с комплектом сменных рабочих органов УНС-5 [11];

• •    плуг-глубокорыхлитель чизельный навесной ПЧН-2,7 [12];

• •    плуг чизельный ПЧ-10-01 [13];

• •    плуг чизельный ПЧ-4,5 [14];

• •    агрегат чизельный АЧП-4,5 [15].

Указанные машины обеспечивают качественное выполнение технологического процесса глубокой обработки почвы, что отражено в протоколах испытаний [6, 7, 8, 9, 10, 11, 12, 13, 14, 15].

По полученным ранее формулам (7), (11), (15) рассчитаем критерии подобия для рассматриваемых машин и результаты сведем в таблицу 2.

Таблица 2

Обозначения	Величина
	ГРН- 3	ПЧН-4,0	ПЧС-10-40	ПУН-08	КАО-10-35	УНС-5	ПЧН- 2,7	пч- 10-01	ПЧ- 4,5	АЧП- 4,5
^ Н-а?	0,10	0,14	0,07	0.08	0.19	0.15	0,08	0.17	0,16	0.16
д-а	1,61	1,33	1,05	1,12	1,03	1,35	1,55	2,79	3,24	1,32
В кг=- а	7,43	10,0	7,21	6,77	10,35	9,76	6,36	11,85	11,25	11,45

Критерии подобия для глубокорыхлителей

Необходимо определить тесноту связи между исследуемыми переменными, представляющими критерий подобия

(табл. 2). Оценочным показателем тесноты связи между случайными переменными является коэффициент корреляции Г:

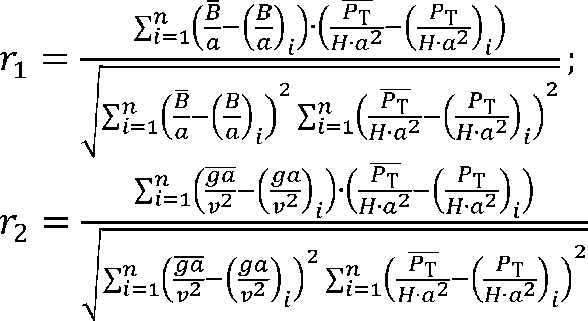
где и = 10 — число машин;

В да

— ; — - среднее значение аргумента;

Рт

- среднее значение функции;

( 5\   /да\

— I ; ( —т I - текущее значение аргумента;

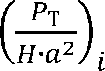
- текущее значение функции.

Коэффициент корреляции Г^ показывает прямолинейность связи между крите-Атриями подобия в зависимости --- — г                               На2

/в\

/ I —^а коэффициент корреляции Г₂ -между критериями подобия в зависимости Рт _ f (ёнЛ

Н-а² ' \v²7

В результате расчётов ту = 0,925; г2 = 0,375. При 0,75 < ц < 0,95 зависи-Рт г (В\ мость---7 — J I — ) является прямолинеи-Н "CL         xCL/ ной; при 0,2 < г2 < 0,5 между исследуе мыми переменными в зависимости

Рт г

---7 = / —7 I существует нелинейная

Н-а^{2 7} \v²7

связь [1].

Следующим этапом является вывод эмпирических формул зависимостей Рт       f в\ Рт      (gct\

---7 — Т \ 1 ^и --- 7 — Г ^—7 ) Основной Н-а^{2 1} \а}   Н-а^{2 }} \v²7

метод формирования эмпирических формул сводится к подбору скелета формулы и нахождению коэффициентов к ней.

Корреляционный анализ позволил

Рт Г (В\ установить, что зависимость ——- = / 1 — 1 является линейной, т.е. её можно записать в виде:

Рт     / Рт \ । fB\

Т^ ⁼ (гФ)п ^{+ Х} \аУ ⁽²⁰⁾ п         X.I1 Cl / Q        хи/

( Рт А где ( —7 ) ; / - коэффициенты эмпириче-\Нп27 о ского уравнения.

Применяя метод наименьших квадра-( РТ А тов, определим I -—7 I и X-\На27 о

Сумма квадратов отклонений измеренных величин (табл. 2) от вычисленного по соотношению (20) должна быть наименьшей:

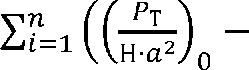
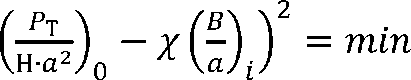
/ Рт А хН-а2/о

Из этого выражения, дифференцируя его сначала по

а затем по X получаем

уравнения:

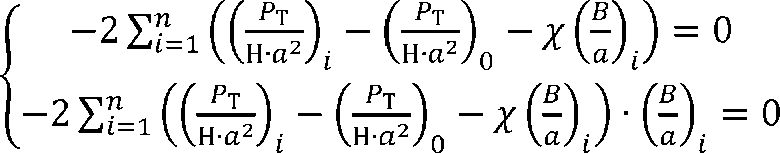
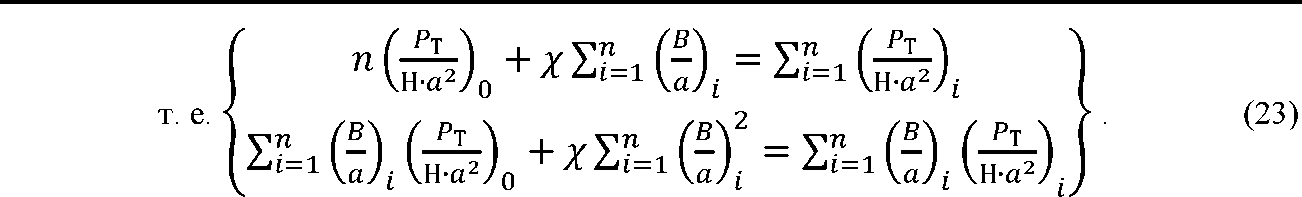
В результате математических преобразований определим коэффициенты эмпириче-

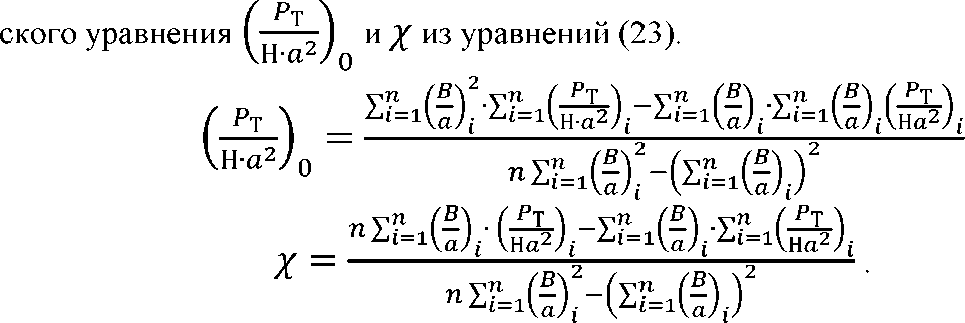
Подставляя данные из таблицы 2 в

формулы (24) и (25), а затем полученные значения в (20), получим эмпирическое уравнение функции---- — / I — I: \С1/

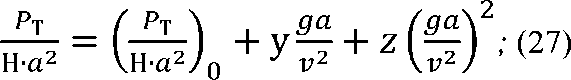
где 2, у, Z - коэффициенты

Рт            В

-4 = 0,019— -0,047.

Рт

Функцию ——-

можно счи

тать квадратичной, т.к. согласно предыду-

щим исследованиям тяговое сопротивление глубокорыхлителя в зависимости от скорости движения изменяется по закону параболы.

В общем виде квадратичную функ-

эмпирического уравнения.

В искомой функциональной зависнет г- (да\ мости ——- — J 1 — 1 отсутствует второй член уравнения (27), поэтому у = 0, а выражение (27) принимает вид:

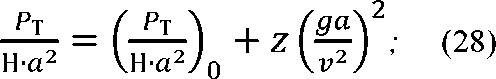
Сумма квадратов отклонений должна

иметь минимальное значение:

цию можно представить уравнением:

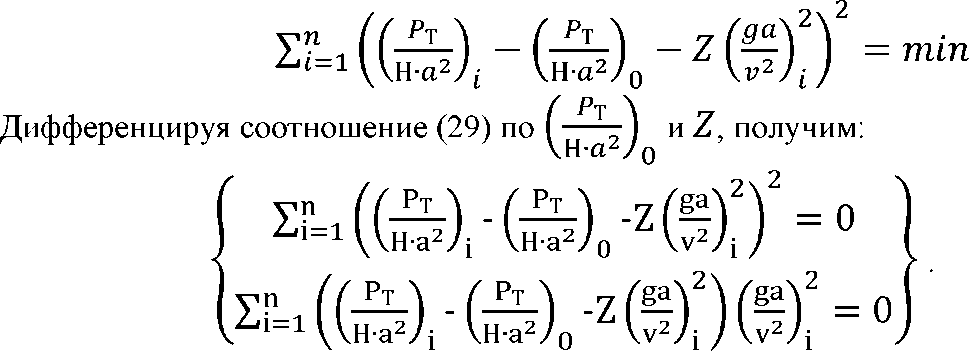
Преобразовав, получим:

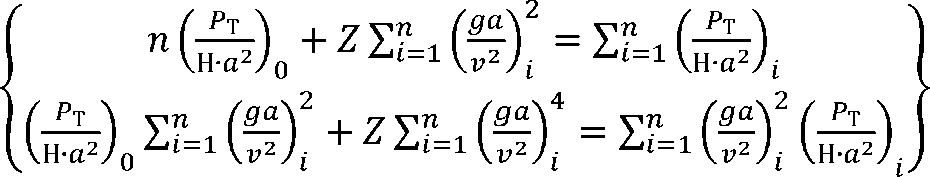
В результате математических преобразований формул (31) запишем выражения для определения коэффициентов эмпирического уравнения

Н"Я2/ Q

и Z;

_vn №П' p_t x _^_vn 7 ^рт 3    №\²

z =----—т-----Ь---- ■      <32)

у 72 / Р^ \ 1/ у 72 /Р^Л )

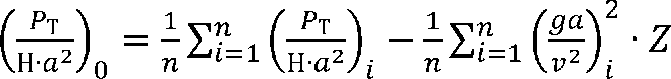
Подставляя данные из таблицы 2 в формулы (32 и (33), а затем полученные значения в (28), получим эмпирическое Р_т rfga\ уравнение функции ^—^ = j \~yj-

-^7= 0,114+ 0,005 f^).      (34)

H-az                   \vz/

Решая совместно уравнения (26) и

(34), получим общее эмпирическое уравне-

Рт _ г (В д-а\ ние функции---т — / I —, —— ): ^к Н-а^{2 J} Ха п² У

= 0,033 + 0,009 —+ 0,002                          (35)

H-a^z                    a          \v² /

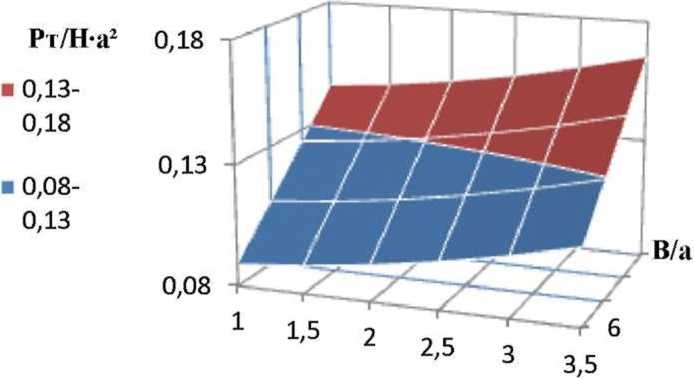
Зависимость (35) графически представлена на рисунке 1 а. Из анализа графика следует, что критерий 71 ^ =  ^2 воз растает интенсивнее с увеличением В                              д-а

ТТ^ = — чем с увеличением Л^ ⁼ ~ Причём при Из = const с увеличением 77*2 величина критерия Л^ возрастает сначала медленно, а затем возрастает более интенсивно. При л₂ = const величина критерия 71 ^ в зависимости от критерия 7Г₃ возрастает равномерно.

С помощью полученного графика можно определить тяговое сопротивление глубокорыхлителя (Яр) задавшись свойствами почвы (/У), параметрами и режимами работы машины (а, В, V ).

Учитывая то, что твёрдость почвы (Н) не должна превышать 4 МПа, а скорость глубокорыхлителя (1?) находится в пределах 7-1 I км/ч (по агротехническим требованиям), решение задачи сводится к выбору ширины захвата машины (S) при заданной глубине рыхления (а) и расчёту тягового сопротивления (Яр). Так, например, для глубокорыхлителя при v = 2 м/с, Н = 3 МПа и а = 0,4 м критерий подобия л3 ^ 1. Выбрав В = 4 м (критерий подобия л2 = 10), определяем по графику л1 = 0,13. При этом Рт = лг- На2 = 62,4 кН (из формулы (7)). А при 5 = 2 м (л2 = 8; Л! = 0,11) Рт = 52,8 Кн.

Таким образом, можно по тяговому сопротивлению для определённого класса трактора выбирать ширину захвата агрега-тируемой машины для глубокой обработки почвы. Выбор тягового сопротивления можно осуществить изменяя ширину за хвата машины, скорость движения и глубину рыхления.

На рисунке 1 б показан график Рт _ г (В д-а\ функции---т — t I —, —— ) при Н-а^{2 v} Ха v² У ¹

п = const, т.е. графически представлена рт ғ зависимость---- = J 1 —) с эмпирически-ми коэффициентами, т.е. уравнение (26). С помощью полученного графика (рис. 1 б) можно упрощённо определить тяговое сопротивление глубокорыхлителя при постоянной скорости движения.

Граница графика на рисунке 1 а определена наибольшим и наименьшим значениями критериев (табл. 1), рассчитанных по данным испытаний.

pT/Ha2=f(B/a, g-a/V2)

а

fT^v2

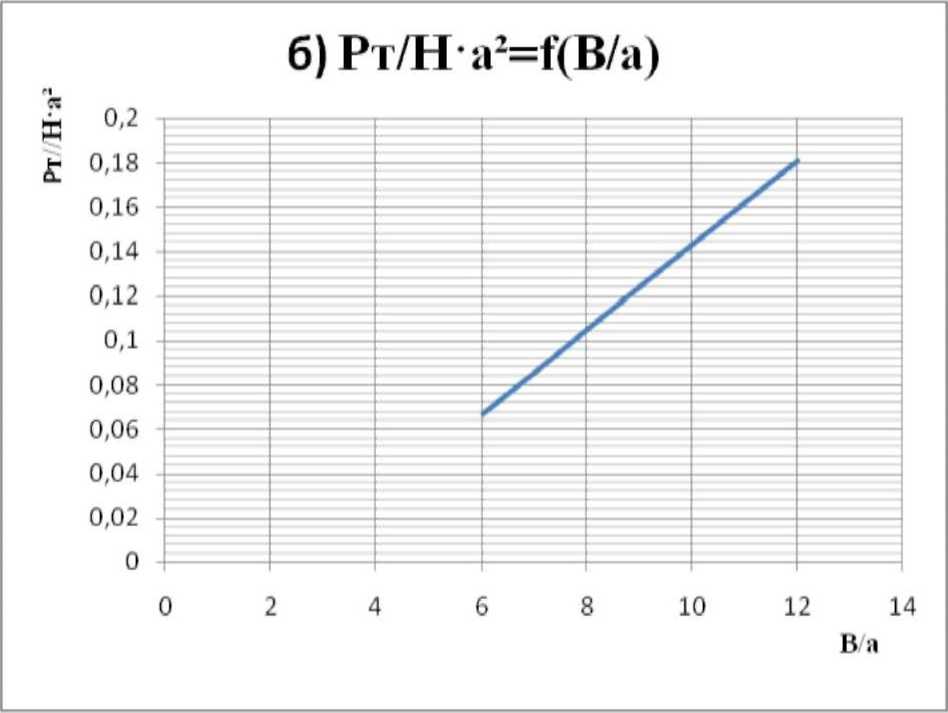
Рис. 1. Графики для определения тягового сопротивления глубокорыхлителей

Зависимость (35) позволяет систематизировать данные экспериментальных исследований и испытаний; раскрывает взаимосвязь параметров и режимов работы глубокорыхлителя с физико-механическими свойствами почвы.

Полученная зависимость (35) может применяться при разработке и обосновании параметров глубокорыхлителей, а также при уточнении режимов их функционирования.