Априорные оценки прямой задачи

• 1 . Постановка задачи

В области Q = (о, H) х (о, T)   изучается распространение влаги в ненасыщенной зоне. Математическая модель одномерной описывается дифференциальным уравнением

задачи

д W _ д д t   д z

(aW) д к

D | +     .

_v   д z J   д z

Начальные и граничные условия задаются в виде соотношений W ( z ,о) = W о ( z ) ,

D (H)д W(H, t) + K (H) = f (t), дz

W (о, t ) = W₂ = const .

(4) используется

Для неустановившихся процессов движения воды численное решение задачи (1)-(4) методом конечных разностей .

Поскольку процесс нахождения решения является итерационным, то вопрос доказательства сходимости его становится обязательным. Для того чтобы доказать сходимость итерационного процесса нам потребуются априорные оценки решения задачи.

Умножим (1) на W ( z , t ) и проинтегрируем по z от 0 до H , по t от 0 до произвольного t . Тогда, учитывая граничные условия (3) и (4), получим

H

H

H /r^ —   HA (5Г/_Ха w I

J dzXW — d T = J d r J — | D ⁽ z )— | о о ^дт      о о 1^д z V      ^д z )

о

о

о

о

v

дК ( z ) | + дz  J

Wdz

Ht

- J dz J

^ о 0

д W² д т

z = H

t          rs jjt           Az          H t / dT = fl D(z)— + K(z)|W   dT -ff| D(z)

о v        ^z          ;   z = о       о о v

Ht

t

z = о

о 0

д W     |д —_лл

+ K ( z ) I dzd T д z        ) д z

t

1i — i² - 1i — >ii² + Jv D < z ) ^ W dT = j K ( z—

2         2         '            d z         ^J_n

о

о

z = H

T + z = 0

t

tH

Г        dW   z = ^H      i-H

+ J D ( z ) — W d T - JJ K ( z ) a          д z      _z =о       ' '

z = о

о 0

^Э — л

---dzd T д z

-I — I

+

t

t

tH

t-                              H

J JD(z)— dT = Jf(t)W(H,t)dT-JJK(z)--dzdr + -W,|| n             dz            n                          (\ (\         d-z           2

о 0

Далее, применяя неравенство Коши, получим

1 W i² + \4Dizi ^ W d r < j ^ ^j ^ )- d r + j v D mn

• W ²( H , t 'W + - W oil +

• ²      0        ^{9 z}      0 #mn     0

  1 ^{t H} K ² ( z )

  ^{2 J J} D ( z )

  
  

  , ,    1 r H ^z J⁹W 1² , ,

  dzd T +      D ( z ) l---I dzd T .

  oo      к z- J

  
  
  
  

Из тождества

W2 (H, t) = J d W (z ’ t)dz = 2 J W (z, t)d W(z, t) dz 0    9z          0          dz следует оценка

HH ²

W ² ( H , t ) <    ,_____ [ W ² ( z, t ) dz +         [ D ( z ) | ^ W I dz .

sJD - о           JD о к dz min 0                        min 0

Подставляя в (5) получим, что t

t

-I W ²|| + -JV D ( z ) d W d T <  J

22          d z

f^^I ) d T + 1| W 0| min

^H + J 0

K 2 ( z ) Tdz + D ( z )

+ . )л« (d W 1 ²

t ₂ d T + — j|| W|| d T . ^£ 0

Пусть £ = —,

тогда

t

-I W ²|| + 1J V D < z ) d W

2¹¹        4 n           d z

d T <  C_x - +

к

min

к

+ D min J

t ₂

+ 4f| W|| dT ,

где

t

H

H

C 1

= max

tHH f f \t)dT, JK2(z)dz,-JW2(z)dz.

0             0             2 0

к

Применяя лемму Гронуолла, получим max| W| |2 +_[ t0

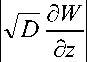
2         ( dt < C2 - +

к

-

min J

Полученный результат оформим в виде леммы 1.

Лемма 1. Если f (t) е L2 (0, T), Wo (z), K(z) e L2 (0, H), то для решения прямой задачи имеют место оценки

max| W | |² + j*

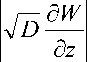
( dT < C 1 + I

Du J

t.

J W ²( H , t ) d T <  C ₃ 1 +

J0                      I

1   )     1

D ™ J T D mr ’