Area Reduction in Redundancy Module for an ECC Based Fault Tolerance in Digital Filters

Electronic circuits are for the most part present in medicinal, automotive, biomedical and medical image processing [1] applications where adaptation to non-critical failure is a subject of concern. In such applications, the circuits give some level of adaptation to internal failure, however it can't give 100% adaptation to non-critical failure yet up to some degree. The need of fault tolerance is increasing as the fault tolerance reliability issues are increasing in CMOS technology. There are many proposed techniques to protect a system from this kind of errors. This can also be done by introducing redundancy at the framework or logic level, to make sure that the faults don’tinfluence the framework [3]. A general method called as TMR (triple modular redundancy) is already in existence. The TMR technique works in such a way that it first triples the outline (design) and then it adds the voting logic to rectify the faults. As this technique triplicates the power and area of the circuit, is not acceptable in some of the cases. The number of parallel filters in the redundancy module increase with the increase in the number of filters in the original module.

As the technology scales down, the need for digital filters is more and there are many applications where these filters operate in parallel. In order to achieve fault tolerance in the device we need a redundancy module as well. But this redundancy module should be as small as possible in terms of size. Here is a table which shows how the number of redundant filters increase with the number of parallel filters.

Table 1. Number of parallel and redundant filters in ECC based technique [2].

S.No.	Number of parallel filters	Number of redundant filters
1.	4	3
2.	8	4
3.	16	5
4.	32	6

From the table above it can be seen that the number develops with the logarithmic in base two on the quantity of filters. Accordingly, the expense is much littler that TMR, in which the quantity of filters is tripled. Digital filters find their usage in most of the signal processing techniques. And there are several techniques to protect them from such errors. Maximum focus is on FIR filters. If p [n] shows the input signal, q [n] shows the output signal and i [Z] shows the impulsive response of the filter [2], and i[Z] is a non zero, for a limited arrangement of tests, the channel is known as finite impulse response filter[2]. Also in [4] the derived relationship expression between the input signal of an FIR filter and its memory component was utilized to recognize the faults. The utilization of diminished accuracy imitations was acquainted with lessen the cost usage of repetition in FIR channels [5].The use of various distinctive implementable structures of FIR filter channels to rectify the errors with a single redundancy module is also into existence[6].The use of FIR characteristics at word level can also be considered for fault tolerance[7]. The use of arithmetic codes is also into existence [8].In all the methods or techniques given so far, only a single filter protection is taken into consideration. As nowadays it is very often to see system devices in which the filters work in parallel. Some of the examples are modern communication systems [9] and filter banks[10].In the event that where the protection is to be done on a more elevated amount the parallel channels ought to be considered as a piece[11].By using this technique used in [11], the cost was reduced as compared to TMR technique. As in [2] a simple technique is proposed to protect the parallel filters. Also in [2] the filters with different input signals and same impulse response are considered. The approach is based on ECC codes in which the each of the input output is considered to be a single bit in ECC code word. This scheme is efficient when the number of filters is large. Further in this paper a new technique is proposed in which the number of filters can be reduced by overlapping technique. And when it is simulated, it gives lesser number of slices, LUTs and multiplexers used.

The rest of the paper is organized as follows:  In section two, we quickly depict the related work of parallel filters having the same impulse response. Section three gives the review of existing technologies. Proposed technique is characterized in section four. The technique of constant multiplication reduction method is also given in this segment, along with the related simulation results. The finalresults are presented in the form of a table which shows the comparison of number of slices and LUTs used in the existing technique and the proposed technique. The conclusion is expressed in section five.

• II.    Parallel Filters Having The Same Impulse Response.

The following equation has been featured by a discrete time filter.

to q [ n ] = Z p[ n -1 И i ]           (1)

1 = 0

Where q [ n ] is the output response, p [ n ] is the input response and i [ l ] is the impulse aftereffect (result) of the filter. When the impulse response i [ l ] is a non zero, for a

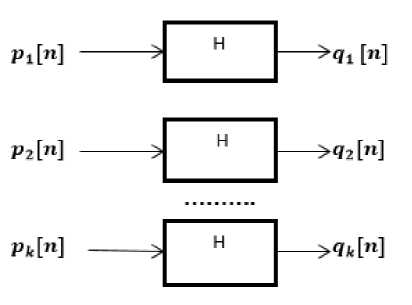
Fig.1. parallel filter which shows the same data response.

finite set of samples it is a FIR filter, else it is an IIR filter [2]. Here a set of parallel filters is considered, where = 4. These parallel filters have different input signals and same impulse response.

Some communications systems use this kind of filters where several channels are in parallel. Some examples are data acquisition and processing applications, where there are several filters with the same data reaction (response).

The unique property of these filters is that the combinational sum of the output signals qi [ n ] can be extracted from the additional sum of the relating inputs pi [ n ] and sifting the obtained signals with the impulse response i [ l ] , which is same for all filters.

q 1[ n ] + q 2[ n ] = £ ( p 1[ n - 1 ] + p 2[ n - 1 ]). i [ 1 ]       ⁽²⁾

l = 0

This scheme will be used in the implementation of the parallel filters by overlapping Technique. The new method is essentially based upon the use of ECCs. A basic ECC makes use of a piece of k bits and creates a square of n bits by including (n-k) equality check bits [12]. The XOR combinations of the data bits is the parity bits. The possible errors can be detected and corrected if the combinations are designed properly. For instance, in a basic hamming code, if k=4 and n=7 , the three equality check bits are c1,c2,c3, and are registered as a component of the information bits d1,d2,d3,d4 as :

c l = d 1 Ф d 2 Ф d 3 c 2 = d 1 Ф d 2 Ф d 4

c 3 = d 1 Ф d 3 Ф d 4           (3)

The aforementioned information and equality bits can be recouped later, regardless of the possibility that there is some blunder in any of the bits. This can be accomplished by reoperating the equality bits and contrasting the outcome and the put away values .If there is any mistake in d1, it will bring about errors in all the three equality bits. Any mistake in d2 will bring about blunder in c1 and c2: a blunder in d3 will influence c1 and c3 , a mistake in d4 will bring about mistake in c2 and c3 . Along these lines the information bits which are having any shortcoming can berecognized and the mistake can be remedied.

There are basically three major codes for redundancy check and out of those, hamming codes are the best suited ones. The generating and the parity check matrixes are as follows:

"1000101"

G =

H =

The syndrome vector is used for correction. It is denoted by . It is to distinguish the bit in error. In software, faults can generate for different alternate purposes [14].

By computing ⋅ and ⋅   , we can obtain the encoding and error correction results respectively. . The ECC strategy can be actualized to the parallel channels by considering an arrangement of check filters rj . If there should be an occurrence of four channels q1, q2, q3, q4 and the hamming codes the check channels would be to

r 1[n] = £ (p1[n -l] + p2[n -l] + p3[n -l]).z[l]  (4)

l = 0

to r 2[ n ] = ^ (p1[ n — l ] + P 2[ n — l ] + P 4[ n — l ]).z'[ l ]   (5)

l = 0

to

r3[n] = £ (p1[n -1] + p3[n -1] + p4[n -1].z[l]) (6) l=0

Therefore,

r1[ n ] = q1[ n ] + q 2[ n ] + q 3[ n ]         (7)

r 2[ n ] = q1[ n ] + q 2[ n ] + q 4[ n ] (8) r 3[ n ] = q1[ n ] + q 3[ n ] + q 4[ n ] (9)

Any error in q 1 will cause errors on the check result of r 1, r 2 and r 3 .Thus different errors on different filters will cause errors on different groups of ri . Thus the errors can be located and detected with the help of ECCs. The overall technique is shown in figure 2. For instance, a lapse on channel q 1 will bring about errorson the checks of r 1, r 2 and r 3 . Essentially, lapses on alternate channels will bring about slips on an alternate gathering of ri . Thusly, as with the customary ECCs, the lapse can be found and revised. The general plan is represented on Fig. 2. It can be watched that rectification is accomplished with just three repetitive channels. For the channels, rectification is accomplished by remaking the mistaken yields utilizing whatever remains of the information and check yields. If in case any error is recognized at q 1 , it can be corrected by making

Z1[ n ] = r1[ n ] - q 2[ n ] - q 3[ n ] (10)

Same way the mathematical statements can be utilized to right faults or errors in whatever remains of theinformation yield. Adaptation to internal failure is a critical element for choosing the usefulness of the framework. Be that as it may, range of the excess module ought to likewise be less.

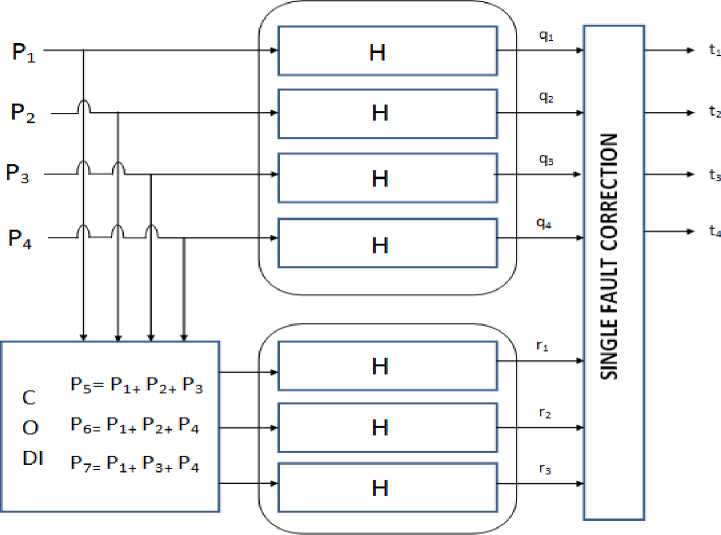
Fig.2. The implemented model for four filters and its redundancy module (three filters).

• III.    Existing Technique

  A more efficient technique of efficient coding was introduced in the above technique by the same author in July 2015[3]. Irrespective of the number of parallel filters the redundancy module had only two redundant filters. But the system has a large complexity though the area is comparably less. Let the redundant filters be and . Then the redundancy filters are given as shown in the below mathematical equations:

v l = p 5 — ( p 1 + p 2 + p 3 + p 4)     (11)

v 2 = p 6 — ( p l + 2 p 2 + 3 p 3 + 4 p 4)   (12)

This was the mathematical model for the redundant module filters which has 4 digital parallel filters. Similarly for 8 parallel filters.

v l = p 9 — ( p l + p 2 + p 3 + p 4 + p 5 + p 6 + p 7 + p 8)

v 2 = p 10 — ( p 1 + 2 p 2 + 3 p 3 + 4 p 4 + 5 p 5 + 6 p 6 + 7 p 7 + 8 p 8)

Similarly, we can calculate for 16, 32 parallel filters. Thus from this we can say that the complexity of the system is more and increases as the number of parallel filters increase.

• IV.    Propposed Technique

As the complexity is increasing the delay will also affect the system. So a new technique is introduced in order to reduce the area of the redundant module by not effecting the functionality of the system. The proposed technique includes the implementation of constant multiplication reduction method with the ECC based technique. Here a constant is multiplied with the filters and the same results are stored in a single Look-up Table (LUT). Here if the quantity of parallel channels (filters) are four then the quantity of repetitive channels will be two.And the complexity of the system will also be less. Memory-based structures are more standard and the expansion total structures and have various distinctive positive circumstances, e.g., more noticeable potential for high-throughput and decreased absence of movement execution, (since the memory-access-time is much shorter than the ordinary duplication time) and are required to have less dynamic force use by virtue of less exchanging practices for memory-read operations veered from the standard multipliers.Memory-based structures are appropriate for some advanced sign preparing (DSP) calculations, which include augmentation with a settled arrangement of coefficients.

A few architectures have been accounted in the writing for memory-based implementation of discrete sinusoidal changes and advanced channels for DSP usage. New ways to deal with LUT-based-increase are proposed to diminish the LUT dimension (size) over that of ordinary design. By odd-various capacity plan, for location length 4, the LUT size is decreased to 50% by utilizing a two-stage logarithmic barrel-shifter and number of NOR entryways, the word-length of the altered multiplication coefficients. One of the structures depends on DA standard, and the other two work on the principle of LUT-based multiplier utilizing the ordinary and the proposed LUT plans. Every one of the structures are found to have the same or about the same cycle periods (frequency), which rely on upon the usage of adders, the word-length and the filter order. Pipelining is used to improve the architecture clock frequency [15]. The standard LUT-multiplier based channel has the same memory essential and the same measure of adders, and less number of data registers than the DA-based layout to the detriment of higher viper widths.Duplication by a consistent can be actualized as an arrangement of additions, subtractions, and movements in custom equipment (e.g., programmable logic gadgets). In a great part of the past examination, movements are expected to incur no expense, and the unpredictability of adders and subtracts are considered the same, so we will allude to both as just a "snake." The objective is to minimize the quantity of adders expected to understand a "multiplier less" circuit for a given constant. While much research has concentrated on the various consistent multiplication (MCM) issue, where a number is increased by a set of constants, numerous applications in advanced sign handling require multiplication by a solitary steady, for example, bringing the dab item with a constant vector in which the multiplicands are autonomous.

The proposed technique is coded in HDL and simulated in Xilinx 12.1i. The simulation results are shown as below. In the below picture we have shown the results for the already existing technique of ECC based fault tolerance in digital parallel filters.

The simulation results are checked against standard inputs by changing different values of the inputs, reset, frequency and clock cycles. These values can be changed by putting different values of force constant and force clock.

Similarly, the proposed technique is coded in HDL and simulated in Xilinx 12.1i. The below picture shows the simulation results for the same.

The simulation results are checked against the standard inputs.

The Xilinx synthesis report was obtained after that. The synthesis report was obtained separately for the existing technique (ECC based) and the proposed one. The results of the synthesis report are tabulated below. The table shows the results for reduction in area of the redundant module filters.The savings are calculated from the results obtained.

Table 2. Comparison of the number of slices and LUTs used.

S.No.	Parameter	Z.gao et.al (2015)[2]	Proposed
1	Slices	469	438
2	LUTs	838	786

This can also be depicted in pictorial form as shown in the below pie chart.

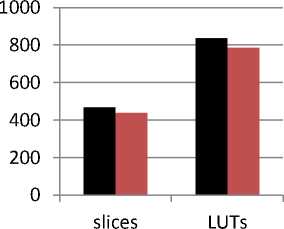
■ existing

■ proposed

Fig.3. Comparison between the number of slices and LUTs used.

• V.    Conclusion

In this paper new technique called constant multiplication reduction method is introduced in the already existing technique of ECC based digital parallel filters. The area optimization is done and the results are shown.Advanced channels are broadly utilized as a part of sign handling and correspondence frameworks. This task proposes a proficient consistent multiplier engineering in view of double basic sub-expression disposal calculation for planning a reconfigurable finite impulse response (FIR) filter. This strategy is equipped for lessening the normal likelihood of utilization or the exchanging action of the multiplier square and snake pieces of channels. FPGA execution consequences of FIR channels utilizing this multiplier demonstrate that the proposed calculation is likewise effective in lessening the normal AREA utilization. The savings are calculated from the above results. We obtained 6.609% savings in resource utilization of slices and 6.205% in LUTs. We exhibit that the Look Up Table (LUT)- multiplier-based technique, where the memory segments store all the possible estimations of aftereffects of the channel coefficients could be a zone compelling unmistakable choice for DA-based blueprint of FIR channel with the same throughput of execution. The proposed arrangement is coded in HDL and simulated using Xilinx 12.1i.