Архитектура нейронных сетей, основанных на физических характеристиках объекта

Физически-информированные нейронные сети (PINN) – это тип универсальных аппроксиматоров функций, которые могут включать в процесс обучения знание любых физических законов, управляющих данным набором данных, и могут быть описаны частичными дифференциальными уравнениями (ЧДУ). Они позволяют преодолеть проблему низкой доступности данных для некоторых биологических и инженерных систем, из-за которой большинство современных методов машинного обучения не обладают достаточной устойчивостью, что делает их неэффективными в этих сценариях. Одной из основных проблем в традиционных численных методах является необходимость большого количества точных и достаточно подробных данных для построения модели. В случае отсутствия или недостатка данных, модель может давать неверные результаты. PINNs предлагают решение этой проблемы, используя физические законы, которые могут быть встроены в нейронные сети в качестве дополнительных условий, которые должны выполняться. Это позволяет использовать ограниченное ко- личество данных для получения точных результатов моделирования. Вместо того чтобы полагаться на большое количество точных данных для обучения сети, PINNs обучают нейронную сеть на основе разреженных и неточных данных и физических законов. Предварительное знание общих физических законов действует в процессе обучения нейронных сетей (NNs) как регулятор, который ограничивает пространство допустимых решений, повышая корректность аппроксимации функции. Таким образом, встраивание этой предварительной информации в нейронную сеть приводит к повышению информативности имеющихся данных, облегчая алгоритм обучения поиску правильного решения и хорошее обобщение даже при малом количестве обучающих примеров. Таким образом, метод PINNs может использоваться для решения сложных задач, таких как прогнозирование погоды, проектирование и анализ инженерных систем, моделирование биологических процессов и т.д.

Преимущества и недостатки PINNs

Преимущества:

• 1.    PINNs могут быть использованы для реше-

• ния различных задач физики и инженерии, включая гидродинамику, механику, электродинамику и многие другие области.

• 2.    Использование PINNs позволяет решать задачи, для которых традиционные методы численного анализа могут быть сложными или неэффективными.

• 3.    PINNs могут быть эффективными для решения проблем, связанных с неоднородными или нелинейными материалами, или структурами.

• 4.    PINNs могут быть использованы для обработки данных экспериментов, которые содержат ошибки или шум, и для извлечения значимых закономерностей из таких данных.

Недостатки:

• 1.    PINNs требуют большого количества данных для обучения, что может быть трудно, если данные являются дорогостоящими для сбора или ограничены.

• 2.    Обучение PINNs может быть сложным и требовать значительных вычислительных ресурсов, так как они объединяют в себе искусственный интеллект и физические уравнения.

• 3.    PINNs могут быть чувствительны к выбору параметров, таких как скорость обучения, размер сети и другие параметры, и требуют тщательной настройки.

• 4.    PINNs могут давать неточные результаты, если используемые физические уравнения недостаточно точны или аппроксимативны.

Функции аппроксимации

Большинство физических законов, которые управляют динамикой системы, могут быть описаны дифференциальными уравнениями в частных производных. Например, уравнения Навье-Сток-са [1] – это набор дифференциальных уравнений, вытекающих из законов сохранения (т.е. сохранения массы, импульса и энергии), которые управляют механикой жидкости. Решение уравнений Навье-Стокса с соответствующими начальными и граничными условиями позволяет количественно оценить динамику потока в точно определенной геометрии. Однако эти уравнения невозможно решить точно, поэтому необходимо использовать численные методы (такие как конечные разности, конечные элементы и конечные объемы). В такой постановке эти управляющие уравнения должны решаться с учетом предварительных допущений, линеаризации и адекватной дискретизации во времени и пространстве. В последнее время решение управляющих дифференциальных уравнений физических явлений с помощью глубокого обучения стало новой областью научного машинного обуче- ния, использующей универсальную аппроксимацию [2] и высокую выразительность нейронных сетей. В целом, глубокие нейронные сети могут аппроксимировать любую функцию при наличии достаточного количества обучающих данных [3]. Однако такие сети не учитывают физические характеристики, лежащие в основе проблемы, и уровень точности аппроксимации, обеспечиваемый ими, по-прежнему сильно зависит от тщательной спецификации геометрии задачи, а также начальных и граничных условий. Без этой предварительной информации решение не является уникальным и может потерять физическую корректность. С другой стороны, нейронные сети с физической информацией (PINN) используют физические уравнения для обучения нейронной сети. А именно, PINN разрабатываются для обучения таким образом, чтобы удовлетворять заданным обучающим данным, а также наложенным управляющим уравнениям. Таким образом, нейронная сеть может управляться с помощью обучающих данных, которые не обязательно должны быть большими и полными [4]. Потенциально, точное решение дифференциальных уравнений может быть найдено без знания граничных условий [5]. Поэтому, имея некоторые знания о физических характеристиках задачи и некоторую форму обучающих данных (даже редких и неполных), PINN может быть использована для поиска оптимального решения с высокой точностью. PINN позволяют решать широкий спектр проблем в вычислительной науке и представляют собой новаторскую технологию, ведущую к разработке новых классов численных решателей для PDE. PINN можно рассматривать как альтернативу традиционным подходам (например, вычислительная гидродинамика), и новые подходы на основе данных для инверсии моделей и идентификации систем [6]. Примечательно, что обученная сеть PINN может использоваться для прогнозирования значений на симуляционных сетках разного разрешения без необходимости повторного обучения [7]. Кроме того, они позволяют использовать автоматическое дифференцирование (AD) [8] для вычисления необходимых производных в дифференциальных уравнениях – новый класс методов дифференцирования, широко используемых для вывода нейронных сетей, которые, по оценкам, превосходят численное или символьное дифференцирование.

Аппроксимация кусочно-функциональных систем с помощью PINNs

Кусочно-функциональная система (PiecewiseFunction System) – это система, которая может быть описана набором функциональных зависимостей, каждая из которых действительна только в определенном диапазоне значений входных переменных. Примером может служить система управления, которая может использовать различные управляющие законы в зависимости от текущего состояния системы. Для аппроксимации кусочно-функциональных систем с помощью PINNs необходимо определить функцию, которая соответствует каждой из областей значений входных переменных [9]. Для этого может быть использована стандартная архитектура нейронной сети, состоящая из нескольких скрытых слоев, которые могут быть соединены с помощью функций активации, таких как гиперболический тангенс. Для обучения PINNs используется комбинация функции потерь, связанной с соответствием модели исходным данным, и функции потерь, связанной с соответствием модели физическим уравнениям системы [10]. Функция потерь, связанная с соответствием модели исходным данным, может быть выбрана в соответствии с постановкой задачи, например, в случае задачи регрессии это может быть среднеквадратичная ошибка между предсказанными и истинными значениями. Функция потерь, связанная с соответствием модели физическим уравнениям системы, может быть задана с использованием дифференциальных уравнений, которые описывают физические законы системы. Для кусочно-функциональных систем это может быть задано следующим образом:

L physics

Z n e x _rf      \ du ^

F\ x,u(x),— i—1J x-    V          dx)

dx .

Идея заключается в том, чтобы минимизировать функцию потерь, связанную с соответствием модели физическим уравнениям системы, используя градиентный спуск. При этом, при обучении PINNs не требуется явно задавать границы между областями значений входных переменных – нейронная сеть сама определит эти границы в процессе обучения.

Пример аппроксимации

Для создания графика и данных нам необходимо выбрать конкретную функцию u ( x ) и правую часть дифференциального уравнения

„ f du F I X, U,----

V    dx

Для примера мы выберем следующую кусоч- но-функциональную систему:

, , [0.5x + 0.2, 0 < x < 5 f (x) =

[ 2 - 0.2 x ,   5 <  x <  10 .

И правую часть дифференциального уравнения:

„ f     du ^ d ² u du ₂

f I x, u,— I — —2“ +2 u .

V     dx ) dx ² dx

Мы будем искать аппроксимацию . функции u ( x ) на отрезке [ 0,10 ] . Результатом будет график (рисунок 1), на котором сплошной линией показана реальная функция u ( x ) , а прерывистой – аппроксимация, полученная с помощью PINNs.

На графике видно, что аппроксимация, полученная с помощью PINNs, достаточно точно приближает реальную функцию u ( x ) на всем отрезке [ 0,10 ] . Однако, в точках разрыва производной аппроксимация имеет небольшие отклонения, так как в этом месте полученные результаты не являются полностью идентичными реальным значениям.

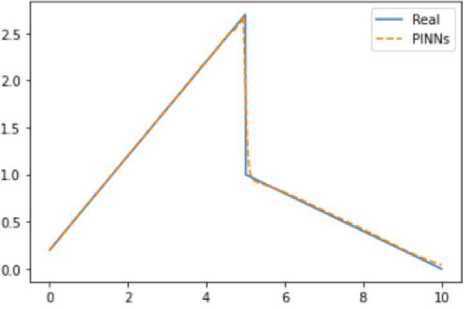
Рисунок 1. Результат аппроксимации

Также можно оценить ошибку аппроксимации на всем отрезке [ 0,10 ] . Результатом будет значение относительной ошибки аппроксимации. В данном случае значение ошибки составляет 0,0261, что говорит о достаточно хорошем качестве аппроксимации. В целом, результаты аппроксимации PINNs могут сильно варьироваться в зависимости от выбранной функции u ( x ) и дифференциального уравнения

f    du

F I x, u,---

V    dx а также от выбранной архитектуры и параметров модели. Однако, метод PINNs является достаточно гибким и может быть применен для аппроксимации широкого класса функций и дифференциальных уравнений.

Заключение

В этой статье мы рассмотрели использование физически информированных нейронных сетей

(PINNs) для аппроксимации кусочно-функциональных систем. Показали, что PINNs позволяют использовать информацию о физических уравнениях системы при обучении, автоматически определять границы между областями значений входных переменных и использовать различные функции активации и скрытые слои.