Архитектурная перспектива в итальянской живописи XIV в

Система представления глубины живописного пространства, развитая в самом конце XIII века Джотто и сразу же восторженно оцененная его совре-

ΣΧΟΛΗ Vol. 14. 1 (2020)                                    © А. И. Щетников, 2020

                 DOI:10.25205/1995-4328-2020-14-1-339-365

340 Архитектурная перспектива в живописи менниками и подхваченная его последователями, внешне имеет много общего с аналогичной системой, характерной для античной настенной живописи. И хотя сам Джотто скорее всего пришёл к своим методам совершенно самостоятельно, ничего или почти ничего не зная о живописи древних, 1 нам надо вкратце сказать, как выглядели перспективные изображения античной эпохи.

По сообщению Витрувия, перспективные изображения впервые появились в античном театре в V веке до н. э., во времена Эсхила; теоретическую основу для таких изображений разработали виднейшие философы той эпохи, Демокрит и Анаксагор. Но как выглядели эти декорации, мы не знаем. В I веке н. э. в Италии перспективными картинами, создававшими иллюзию уходящего за стену пространства, украшались покои богатых домов. Помещений с такими изображениями сохранилось совсем немного, причём все они были раскопаны в XVIII–XIX веке, а до этого были погребены под землёй; это несколько помпейских вилл и несколько императорских построек на Палатинском холме в Риме, в том числе дом Августа, фреска из которого воспроизведена на рис. 1. Красным цветом здесь показаны прямые линии, которые мыслятся уходящими вдаль от зрителя под прямым углом к плоскости картины; такие прямые в теории перспективы называются ортогоналями . В отличие от классической линейной перспективы, ортогонали здесь не сходятся в одну точку, лежащую на линии горизонта, но образуют пары, симметрично наклонённые к оси картины. В искусствоведении такая система представления глубины архитектурного пространства получила название «рыбья кость». ² К детальному описанию заложенных в её основу принципов я вернусь ниже.

Рис. 1. Фреска в доме Августа. I век н. э.

В средневековом христианском искусстве интерес к передаче глубины пространства проявляется весьма слабо. И хотя у ближайших предшественников Джотто можно обнаружить некоторые зачатки «протоперспективы», однако итальянская живопись позднего средневековья по большей части обходилась совсем без этого приёма. На алтарных клеймах таких мастеров середины XIII века, как Бонавентура Берлингьери и Коппо ди Марковальдо, действие очень часто происходит на фоне разных строений, но все они показаны достаточно условно, и всегда — снаружи и фронтально, в духе предыдущей византийской традиции и без каких-либо элементов перспективы; что касается интерьеров, то их здесь практически нет, и введение в живопись действия, представленного в интерьере помещения, всецело принадлежит одному лишь Джотто.

В качестве характерного примера архитектурной «протоперспективы» можно рассмотреть мозаику Уверение Фомы, входящую в грандиозный цикл мозаик, выполненный в кафедральном соборе Монреале на Сицилии анонимными мастерами в промежуток между 1183 и 1189 годами (рис. 2). Явление Христа перед апостолами происходит здесь на фоне широкого двора, ограниченного по бокам двумя симметричными флигелями; уходящие вдаль карнизы этих флигелей показаны наклонными линиями. Глубина собственно архитектурной части изображения невелика, так что представленные на фреске человеческие фигуры находятся не внутри намеченного перспективой двора, но перед ним, а вся архитектура выполняет по отношению к этим фигурам роль театральных декораций. Впрочем, этот приём для мозаик собора Монреале скорее случаен, поскольку большая часть изображений здесь выполнена на золотом фоне и лишена архитектурного задника; а там, где он появляется по сюжету, изображение обычно лишено перспективных элементов; кроме того, здесь присутствуют и предметы, изображённые в традиции «обратной перспективы» (расширяющаяся назад трапеция стола в мозаике Изгнание из храма, обращённый к ангелам полукруг столешницы в Троице).3

Рис. 2. Уверение Фомы.

Мозаика в храме Монреале, 1183–1189.

Схожее взаимное расположение архитектурных элементов и человеческих фигур мы видим на мозаике Пьетро Каваллини Рождество Богородицы , выполненной в римской церкви Санта-Мария-ин-Трастевере в 1291 году — то есть всего за несколько лет до фресок Джотто (рис. 3) . Задней декорацией сцены здесь служит изображение двух проёмов между опорами, перекрытыми балками с кессонированными потолками. Линии карнизов обоих проёмов при их продолжении встречаются в точках, лежащих на оси симметрии каждого проёма.⁴ И опять, действие картины происходит не внутри имеющего совсем небольшую глубину архитектурного пространства, которое тем не менее можно трактовать как интерьер, но на его фоне.

Рис. 3. Пьетро Каваллини . Рождество Богородицы .

Мозаика в церкви Санта-Мария-ин-Трастевере, Рим. 1291.

Первым размещать фигуры людей внутри пространства с архитектурно оформленной глубиной стал в конце XIII века знаменитый флорентийский живописец Джотто ди Бондоне. Действие написанных им сцен зачастую происходит внутри стилизованных архитектурных объёмов, так что на картине перед зрителем предстаёт своего рода мистериальный театр с декорациями, расставленными по бокам и на заднем плане.⁵

Основные принципы развитой Джотто системы уже в первом десятилетии XIV века усвоили другие итальянские художники, такие как безымянный «мастер святой Цецилии», написавший свой алтарь с изображением этой святой до 1304 года, и виднейший мастер сиенской школы Дуччо ди Буонинсенья, Маэста которого датируется 1308 годом. Эту же систему мы встречаем и у других итальянских живописцев XIV века, и она остаётся ведущей в итальянской живописи по меньшей мере до 1425 года, когда в кругу флорентийских художников были открыты правила линейной, или научной перспективы . Более того, некоторые художники, такие как сиенский мастер Джованни ди Паоло, сознательно пользовались этой системой вплоть до второй половины XV века.

Будучи в некоторых деталях похожей на линейную перспективу, система представления глубины пространства, характерная для Джотто и его последователей, имеет с ней не так много общего. Прежде всего, здесь нет ключе- вой для линейной перспективы идеи о том, что картина является изображением некоторого реального пространства, как оно представляется неподвижному глазу, рассматривающему это пространство с определённой точки и устремившему взгляд под прямым углом к плоскости картины в направлении линии горизонта. Соответственно, здесь нет и характерного для линейной перспективы схождения всех ортогоналей в противостоящую глазу точку на линии горизонта. Однако эта система изображения глубины архитектурного пространства всё же является непосредственной предшественницей линейной перспективы, и потому о ней также можно говорить как о предренессансной перспективе.

Представляя собой особый изобразительный язык, предренессансная перспектива интересна своими внутренними противоречиями: художник, следуя правилам этой системы, зачастую попадает в ситуацию, когда эти правила вынуждают его делать неправдоподобные изображения; и порой ему приходится корректировать правила, чтобы выйти из возникшего затруднения. Именно этому мыслительному процессу осознания противоречий и работы с ними я собираюсь уделить основное внимание в настоящей статье. Эта мыслительная деятельность, вызревающая внутри художественной практики, в своих глубинных основах может считаться математической, предполагающей особую связь посылок и следствий, — причём возникающая здесь математика не привносится извне, из чтения геометрических трактатов древних, но появляется из самой сути умного художественного ремесла.6

По этой причине дальнейшее изложение будет вестись не в хронологическом порядке, но в порядке усложнения изобразительных проблем. Некоторые из этих проблем Джотто умел решать ещё в 1300 году, но это не означает, что следующие за ним художники не сталкивались с ними вновь; и зачастую им приходилось решать эти проблемы заново. Это многократное переоткрытие изобразительных приёмов я представляю себе таким образом: художник обнаруживает некоторое затруднение и придумывает приём, позволяющий с ним справиться, — но единственным результатом его трудов в итоге оказывается сама картина, а технические ухищрения остаются в его памяти и передаются разве что изустно ближайшим ученикам. Художник из другого города видит картины, сделанные первым мастером, они ему нравятся, и он хочет им подражать; но, глядя на картину, он не видит ни исходных затруднений, ни тех приёмов, с помощью которых они были разре- шены — и ему приходится переоткрывать всё заново. Конечно, через какое-то время открытые техники станут всеобщим достоянием, но это происходит не сразу, так что мы можем видеть в работах разных художников одну и ту же общую для всех ситуацию, и смотреть, как они с ней справлялись.

Что касается литературы по данному вопросу, она немногочисленна. Конечно, все писавшие о Джотто отмечали и его новшества в изображении глубины пространства, и его не всегда правильную систему перспективы. Однако устройству этой системы и анализу тех парадоксов, к которым она порой приводит, посвящено совсем немного работ. Интересная статья фон Керна (Kern 1912) впоследствии была почти забыта, хотя её и упоминает в своём обстоятельном исследовании Эрвин Панофский (Панофский, 2006). Истории предренессансной перспективы посвящена весьма содержательная серия записей Тихона Токарева в Живом журнале tito0107.livejournal.com, на которую я также хочу обратить внимание читателя.

Система перспективы «рыбья кость»

В развитой в живописи XIV в. системе представления картинного пространства интерьер, внутри которого происходит действие, изображается по большей части в двух основных ракурсах, каждый из которых закреплён за тем или иным сюжетом. Это или закрытое помещение с осевой симметрией, у которого удалена передняя стенка, или лоджия с колоннами, на которую мы глядим сбоку под углом; при этом в обоих случаях мы видим и потолок помещения, на который смотрим снизу, и пол, на который смотрим сверху. В качестве основы для системы «рыбья кость» рассмотрим сначала картину с осевой симметрией помещения.

Представим себе, что мы хотим изобразить прямоугольную комнату, как будто у неё снята ближняя к нам стенка и мы заглядываем внутрь неё через открытый проём, находясь напротив его середины. Границы этого проёма естественно совместить с границами картины. При этом задняя стена комнаты изображается ещё одним прямоугольником меньшего размера, а уходящие вдаль стыки боковых стен с полом и потолком (мы будем называть эти линии главными ортогоналями ) — прямыми линиями, соединяющими углы переднего и заднего прямоугольников. Именно такую простейшую схему сведения ортогоналей мы видим на алтарной доске Бернардо Дадди Ангельская скорбь св. Фомы Аквинского , написанной в 1338 году (рис. 4) .⁷

Рис. 4. Бернардо Дадди. Ангельская скорбь св. Фомы Аквинского . 1338.

Заметим, что если верхние и нижние стыки боковых стен сойдутся на оси картины не в одну, но в две точки, лежащие на разной высоте (рис. 5, а), задняя стена комнаты будет иметь другие пропорции сторон, нежели передняя; на рисунке такая сильно искажённая пропорция задней стены показана пунктирным прямоугольником. Чтобы картина не выглядела слишком неправдоподобной, точки схода верхних и нижних стыков не должны сильно отстоять друг от друга, либо глубина изображаемого пространства должна быть небольшой, чтобы отличие пропорций переднего и заднего прямоугольников не было слишком заметным. А ещё художник может заслонить нижние стыки какими-нибудь предметами, и тогда непропорциональность стен не будет видна глазу, и её можно будет обнаружить только специальным построением.

Теперь представим, что мы направили свой взгляд в верхний левый угол комнаты, и видим карниз, идущий по левой стене под линией её стыка с потолком, либо уходящие вдаль балки на потолке. Если комната симметрична, в точности такую же картину мы увидим и в верхнем правом углу картины, если посмотрим в его сторону. Изобразительное правило системы «рыбья кость» состоит в том, что все ортогонали, зрительно привязанные к каждому из углов картины, изображаются семейством параллельных прямых, так что каждый угол помещения изображается как бы в отдельной аксономет- рии. Получившаяся схема имеет вид обглоданного рыбьего скелета (рис. 5, б), по которому эта система и получила своё название. Такая же «рыбья кость», только перевёрнутая остриём вверх, строится и для ортогоналей, привязанных к стыкам боковых стен с полом помещения.

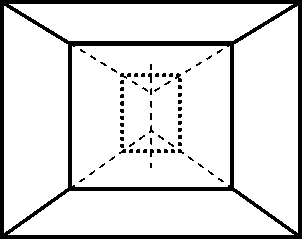
Рис. 5. К образованию системы «рыбья кость»:

(а) верхние и нижние главные ортогонали обычно имеют две разных точки схода на центральной оси, и при большой глубине изображения задняя стена имеет пропорции, сильно отличные от передней; (б) все ортогонали, «привязанные» к каждому из углов картины, изображаются семейством параллельных прямых.

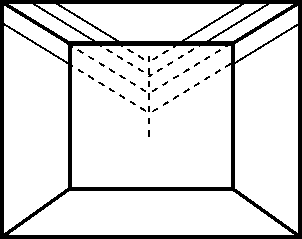
Б. Раушенбах (1980, 66–67) называет такую изобразительную систему «схемой изображения интерьера путём локальных аксонометрий» и приписывает её выбору подвижной точки зрения, когда правый верхний угол комнаты изображается при виде слева снизу, и т. д. Но что представляет собой каждая локальная аксонометрия, как изобразительный приём? В ней соединяются знание художника об изображаемом предмете и то, как он представляет себе то, что он видит. Во-первых, художник знает, что все карнизы, близкие к линии стыка боковой стены и потолка, в действительности параллельны друг другу (впрочем, он знает это и вообще о всех ортогоналях, но это уже другое, более рафинированное и теоретическое знание). Во-вторых, он знает, что такие линии, если рассматривать их издалека, не только являются, но и выглядят параллельными. Поэтому он хочет видеть их параллельными и на картине, что и задаёт ту априорную схему, в которую он вкладывает ортогонали изображаемого интерьера.

Хорошим примером реализации схемы локальных аксонометрий служит Тайная вечеря сиенского художника Липпо Мемми, написанная в городском соборе Сан-Джиминьяно (рис. 6). Плоский потолок поддерживается четырьмя консолями, которые мыслятся отстоящими друг от друга на равные расстояния. Обозначив границы потолка, художник делит линию стену на три секции одинаковой ширины. Затем он проводит через средние отметки две ортогонали средних консолей, выводя их параллельно ортогоналям крайних консолей. В результате средняя панель потолка представлена на картине трапецией, а крайние панели — параллелограммами. При этом передняя линия потолка оказывается разделённой на три неравные части — её средняя часть заметно больше крайних. Однако это неравенство не вос- принимается художником как неправильное: ведь средняя панель находится ближе к нам, мы и должны видеть её под большим углом!

Рис. 6. Липпо Мемми. Тайная вечеря .

Фреска в Дуомо Сан-Джиминьяно, между 1330–1350.

В соответствии с принципом «рыбьей кости» Мемми проводит также нижние ортогонали картины — края лавок и стола, ленты на скатерти. Здесь уклон больше, чем на потолке, словно мы глядим на происходящее с достаточно высокой точки. Это позволяет визуально поднять задний ряд сидящих над передним рядом, так что передние фигуры апостолов не заслоняют тех, кто сидит сзади, в соответствии с одним из традиционных иконографических вариантов этой сцены.

В качестве более позднего примера картины с осевой перспективой рассмотрим фреску Джованни да Милано Изгнание Иоакима из храма (рис. 7) . Действие помещено здесь в структуру помещения с готическими колоннами; все детали карнизов и капителей этих колонн выстроены «ёлочкой», направленной остриём вниз и имеющей приблизительно один и тот же наклон; детали нижних плинтусов выстроены «ёлочкой» такого же наклона, направленной остриём вверх.

Рис. 7. Джованни да Милано. Изгнание Иоакима из храма . Фреска в капелле Ринучини, Санта Кроче, Флоренция, 1365–1370.

Вторая реализация схемы «рыбьей кости», характерная для изображения лоджии или нескольких примыкающих друг к другу помещений, представляет собой как бы половинку изображения с осевой симметрией. Такая схема в самом простом её варианте осуществлена на Благовещении Бернардо Дадди (рис. 8) . Здесь все верхние и все нижние ортогонали задают свою локальную аксонометрию для верхней и нижней частей картины соответственно, так что разметка потолка с кессонами и пола в клетку не представляет для художника никакой сложности.

Рис. 8. Бернардо Дадди. Благовещение . 1335.

Потолок с кессонами и клетчатый пол

Настоящие проблемы системы «рыбья кость» начинаются, когда художник хочет изобразить потолок с клетками кессонов, или такой же клетчатый пол на картине с осевой симметрией. Такое странное изображение кессонов мы уже видели выше на мозаике Пьетро Каваллини; посмотрим теперь на Тайную вечерю сиенского художника Уголино ди Нерио, написанную около 1325 года для алтаря церкви Санта-Кроче во Флоренции (рис. 9). Изобразив стены и потолок таверны, в которой происходит трапеза, художник проводит ортогонали потолка, отстоящие на равные расстояния друг от друга. Все ортогонали левой половины потолка в соответствии с принципом «рыбьей кости» проводятся параллельно линии стыка потолка с левой стеной. Точно так же все ортогонали правой половины потолка проводятся параллельно линии стыка потолка с правой стеной. В результате такого построения две ортогонали в центральной части потолка встречаются друг с другом непосредственно на задней стене помещения, образуя невозможное изображение.8

Рис. 9. Уголино ди Нерио. Тайная вечеря .

Алтарь в церкви Санта-Кроче во Флоренции, ок. 1325.

Эта же проблема неправдоподобного схождения близких к оси картины ортогоналей встречается и у более поздних художников, вплоть до середины XIV века. Впрочем, такие мастера, как Джотто и Дуччо, научились решать её гораздо раньше. Посмотрим, как Дуччо изображает сетку кессонов в Тайной вечере на одной из досок сиенской Маэсты (рис. 10). Ортогонали консо- лей он проводит по правилу «рыбьей кости». Кессоны боковых панелей расчерчиваются тоже по правилу «рыбьей кости», в локальной аксонометрии, параллельно сторонам параллелограммов. А вот ортогонали центральной панели Дуччо сводит в одну точку, положение которой задаётся пересечением ограничивающих эту панель карнизов.9

Рис. 10. Дуччо. Тайная вечеря .

Алтарь Маэста в Сиенском Дуомо, 1308–1311.

При взгляде на картину Дуччо мы сразу же видим точку схода этих ортогоналей, потому что мы привыкли к картинам, построенным по принципу линейной перспективы, равно как к фотографиям, фиксирующим это схождение по законам оптики. Однако строил ли эту точку схода сам Дуччо, и осознавал ли он её значение в пространстве картины? Похоже, что он этого не делал, поскольку для выправления ортогоналей у него имелся другой путь рассуждения и действия. Прямоугольник потолка между двумя карнизами изображается на рисунке трапецией. Линии, отделяющие один кессон от другого, должны делить заднее основание этой трапеции на пять равных частей. Но точно так же они должны делить на пять равных частей и переднее основание. Произведём это деление и соединим отмеченные точки прямыми линиями — и это построение решает задачу. Проведённые таким образом ортогонали оказываются сходящимися в одну точку (рис. 11). Одна- ко мы их через эту точку не проводили: при аккуратном построении они встретятся в ней сами, даже когда мы об этой точке не думали.

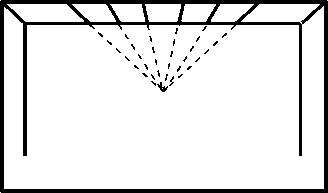
Рис. 11. Ортогонали потолка, построенные по схеме пропорционального деления, с необходимостью сходятся при их продолжении в одну точку.

Осуществляя схожее построение на доске Христос перед Анной , Дуччо расчерчивает сходящимися линиями весь потолок целиком (рис. 12) . Правда, ортогонали здесь проведены не слишком аккуратно, и они не сходятся в одну точку, что заставляет нас подозревать, что и в других досках Маэсты Дуччо сводил их не точным пропорциональным делением переднего и заднего отрезков, а «на глаз».

Рис. 12. Дуччо. Христос перед Анной . Алтарь Маэста в Сиенском Дуомо, 1308–1311.

Удачный пример геометрически правильного схождения ортогоналей потолка можно видеть на фреске Джотто Христос среди учёных, написанной около 1320 года в нижней церкви св. Франциска в Ассизи (рис. 13). Здесь они сходятся в одну общую точку не только на центральной, но и на боковых панелях.10

Рис. 13. Джотто. Христос среди учёных .

Фреска в нижней церкви св. Франциска, Ассизи, ок. 1320.

Ортогонали капителей колонн в двух средних и двух крайних рядах при этом тоже сходятся в одну точку, но эта точка лежит ниже от точки схода ортогоналей кессонов потолка: принцип «рыбьей кости» выправляется там, где он приводит к очевидно парадоксальным результатам, но в целом он продолжает действовать! Центр схождения ортогоналей объединяет пока что элементы потолка, но не всей картины. И его положение определяется отнюдь не местонахождением глаза, созерцающего пространство картины, как это происходит при настоящей линейной перспективе, но тем, под каким углом наклона были проведены боковые ортогонали, и на каком расстоянии от передней стороны коробки помещения была проведена её задняя сторона.

Сводчатый потолок

На фреске Джотто Утверждение устава из верхней церкви св. Франциска в Ассизи, написанной около 1300 года (рис. 14) , мы видим ещё один пример усиленного схождения ортогоналей, близких к оси картины. Попробуем понять, что могло привести художника к такому решению в этом случае.

Рис. 14. Джотто. Утверждение устава .

Фреска в верхней церкви св. Франциска, Ассизи, ок. 1300.

Пусть задние концы консолей разделят соединяющую их линию на три равные части. (Такие прямые линии, перпендикулярные к ортогоналям и тем самым параллельные плоскости картины, в теории перспективы называются трансверсалями .) Допустим, что ортогонали двух средних консолей будут проведены по правилу «рыбьей кости», параллельно крайним консолям. В таком случае передние концы консолей разделят свою трансверсаль на неравные части. Но тогда получится, что полукружия сводов в задней плоскости будут иметь равные диаметры, а в передней плоскости — неравные диаметры (рис. 15, а). Но ведь в действительности диаметры всех полукружий мыслятся равными! Поэтому Джотто делит на три равных части и переднюю, и заднюю трансверсали, как это было и в случае кессонирован-ного потолка, в результате чего центральные ортогонали приобретают больший уклон (рис. 15, б).

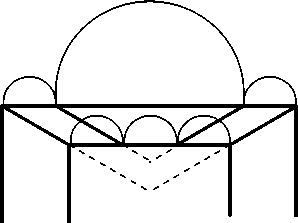
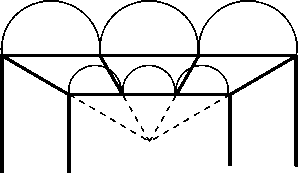
Рис. 15. Потолок с несколькими сводами:

(а) неправдоподобное решение; (б) правдоподобное решение.

Такое же изображение сводчатого потолка мы видим и на ряде других картин Джотто, написанных до 1300 года — на фреске Сошествие Святого Духа над входом в верхнюю церковь св. Франциска, и на ещё одном Утверждении устава , написанном на пределле панели Стигматизация св. Франциска (рис. 16) . В последнем случае на картине изображены и консоли с пятью сводами равной ширины, и широкий потолок с уходящими вдаль балками — поистине, Джотто в 1300 году умел решать такие изобразительные задачи геометрического характера, которые ставили в тупик и многих художников, работавших после него.

Рис. 16. Джотто. Утверждение устава .

Алтарь Стигматизация св. Франциска, пределла, ок. 1300.

Кессоны на двускатном потолке

Ещё одна любопытная неувязка линий потолка произошла на фреске сиенского художника Никколо ди Сенья Явление св. Григория перед больной св. Финой , находящейся в Дуомо Сан-Джиминьяно (рис. 17) . Пространство позади человеческих фигур разделено здесь на три нефа — узкий центральный и несколько более широкие боковые; боковые нефы перекрыты плоскими горизонтальными потолками, а центральный неф — двускатным потолком. Все потолки разбиты на клетки кессонов. Ортогонали кессонов в боковых частях потолка проведены по принципу локальной аксонометрии; ближе к центру эти части потолка правдоподобно закрыты вертикальными стенками, отделяющими центральный неф от боковых. Но как быть с кессонами центральной двускатной части? «Рыбья кость» очень сильно заужает заднюю стену центрального нефа, так что когда задние линии скатов разделены на три равных части, передние линии приходится делить на шесть частей такого же размера. Художник вышел из создавшегося положения довольно лихо, составив потолок центральной части из трёх квадратных секций три на три клетки: при этом центральная секция оказалась разделённой коньком потолка по диагонали, и одна её половина отнесена к правому, а другая — к левому скату, что создаёт невозможную фигуру.¹¹

Рис. 17. Николо ди Сенья. Явление св. Григория перед больной св. Финой . Фреска в Дуомо Сан-Джиминьяно, между 1330–1350.

Верную стыковку кессонов на верхнем стыке скатов в аналогичном случае даёт Дуччо в Неверии Фомы (рис. 18) . Он расплачивается за неё тем, что проводит все ортогонали кессонов параллельно линии конька, в своей локальной аксонометрии, без какого-либо схождения к оси картины. Поэтому ему приходится закрыть нижние части скатов нимбами апостолов. В противном случае ортогональ нижнего края ската, проведённая под уклоном, оказалась бы не согласованной по направлению с ортогоналями кессонов, и невозможная фигура возникла бы в этом месте картины.¹²

Рис. 18. Дуччо. Неверие Фомы .

Алтарь Маэста в Сиенском Дуомо, 1308–1311.

Расположение колонн

Любопытные невозможные фигуры возникают на изображениях интерьеров с колоннами. Классический пример такой невозможности мы видим на доске Дуччо Обвинение Христа фарисеями (рис. 19). Иисус, Понтий Пилат, толпа солдат за их спиной — все они стоят на уровне переднего ряда ко- лонн лоджии.13 А где же средняя колонна этого ряда? Её ствол уходит за спины толпы, хотя ему положено стоять спереди; и мы не видим её основания, хотя оно должно находиться на одной линии с двумя другими колоннами.

Рис. 19. Дуччо. Обвинение Христа фарисеями . Алтарь Маэста в Сиенском Дуомо, 1308–1311.

Ещё одна доска Маэсты Дуччо с невозможным расположением колонн показана на рис. 20. Если ближний ряд колонн находится позади ступеней, на которых сидит Иисус, то где же тогда стоят задние колонны? И ещё, если ортогонали клетчатого пола даны в локальной аксонометрии, соответствующей взгляду сверху и справа, то как ортогонали капителей оказались изображенными в аксонометрии, соответствующей взгляду снизу и слева? Глядя на эти доски, хочется предположить, что Мауриц Эшер, с 1923 по 1935 год живший в Италии, в том числе и в Сиене, видел эти работы и впоследствии использовал их схемы в своих «невозможных» гравюрах, таких как Бельведер (1958).

Рис. 20. Дуччо. Христос перед мудрецами .

Алтарь Маэста в Сиенском Дуомо, 1308–1311.

Более тонкий сбой в расположении колонн можно видеть на фреске Пьетро Лоренцетти Бичевание Христа (рис. 21) . При сильном схождении верхних и нижних ортогоналей вглубь картины человеческие фигуры переднего и заднего плана изображены здесь практически одинаковыми по величине, так что задние фигуры почти упираются головой в потолок.¹⁴ Теперь посмотрим на уходящий вдаль центральный ряд колонн. Поскольку две колонны и пилястра подпирают одну и ту же потолочную балку, их основания на полу также должны стоять в одном и том же ряду квадратов. Однако ортогонали квадратов уходят в глубину картины круче, чем ортогонали потолка, не будучи согласованы друг с другом. Поэтому художник сдвигает среднюю колонну и пилястру вправо. Чтобы соблюсти правильность построения, ему надо было изобразить нижнюю ортогональ так, как она проведена на рисунке красной линией. Но тогда и ноги у фигур Христа и двух бичующих надо было отодвигать дальше от переднего края лоджии.

Рис. 21. Пьетро Лоренцетти. Бичевание Христа .

Фреска в нижней церкви св. Франциска, Ассизи, ок. 1320.

Рассмотрим теперь алтарный триптих Рождество Марии , также написанный Пьетро Лоренцетти (рис. 22) . В этой работе художник добился немалого пространственного иллюзионизма, объединив три доски алтаря единым изображением, как бы видным через раму со стрельчатыми сводами: на одной доске мужчины сидят в небольшой комнате в ожидании, а на двух других изображено помещение, в котором находятся женщины. И всё же, проведём красными прямыми «рёбра» комнаты, в которой происходит действие. Если комната ограничена плоскостями этой коробки, то где же тогда находится ложе, на котором возлежит св. Анна? Ему нет места в комнате, оно расположено как бы за её задней стеной. И как соотносятся между собой глубина боковой и задней комнат? Видно, что художнику хочется увеличивать глубину картины, но наличные техники для этого не очень пригодны, что приводит к странному конфликту одновременной реалистичности и невозможности изображения.

Невозможные фигуры такого рода не были редкостью на средневековых фресках и миниатюрах. Но там мы их воспринимаем в рамках общей условности изображения.15 Здесь же художник стремится представить интерьер достаточно реалистичным — и одновременно отказывает ему в этой реалистичности, опираясь на иконописную изобразительную традицию и отталкиваясь от неё.

Рис. 22. Пьетро Лоренцетти. Рождество Марии . 1342.

Проблема диагоналей

Допустим, что мы уже научились проводить ортогонали потолка или пола так, чтобы они сходились в одну точку. Но тогда возникает следующий вопрос: на каких расстояниях друг от друга надо проводить линии, идущие под прямым углом к ортогоналям (такие линии в теории перспективы называют трансверсалями ), чтобы получившаяся сетка служила изображением равных квадратов, или хотя бы равных прямоугольников? Ясно, что расстояния между соседними трансверсалями должны уменьшаться по какому-то единообразному правилу — но по какому именно?

Первую в истории живописи попытку передачи глубокой перспективы за счёт квадратной сетки пола мы обнаруживаем на картине Амброджо Ло-ренцетти Благовещение , написанной в 1344 году (рис. 23) .

Все ортогонали клетчатого пола аккуратно выведены здесь по линейке к центру квадрата картины; ясно, что художник не занимался пропорциональным делением дальнего края пола, как оно было описано выше, но сразу же поставил точку схода в центр картины, и вывел из неё ортогонали к разметке переднего края. Однако вряд ли будет правильным сказать, как иногда пишут, что «Лоренцетти открыл точку схода»; скорее, он открыл приём, позволяющий правильно разметить ортогонали пола так, чтобы они делили любую трансверсаль на равные отрезки.

Рис. 23. Амброджо Лоренцетти. Благовещение . 1344.

Красным цветом проведены прямые диагонали прямоугольника; зелёным — ломаные линии, составленные из диагоналей отдельных клеток.

Однако перейдём к вопросу о расстояниях между последовательными трансверсалями. На картине Лоренцетти эти расстояния постепенно уменьшаются по мере перехода от переднего плана к заднему. Но каково правило их уменьшения? Разлиновка клеток пола выглядит на первый взгляд весьма правдоподобной, во всяком случае отторжения у нас она не вызывает. И тем не менее здесь есть одна несообразность, которую можно выявить, к примеру, следующим построением. Глубина пола на картине Ло-ренцетти составляет 8 клеток. Выделим на полу прямоугольник 8 × 8 клеток, и проведём в нём две диагонали. Эти диагонали в реальности пересекаются в центре выделенного прямоугольника. Значит, через точку их пересечения должна проходить трансверсаль, которая делит исходный прямоугольник на две равные прямоугольные половины. Однако эта трансверсаль проведена у Лоренцетти заметно ближе к переднему плану картины. А если мы проведём диагонали в каждой диагональной клетке, составленная из них линия окажется не прямой, но ломаной.

Но если диагонали должны быть прямыми, то именно это требование прямизны можно сделать основой решения задачи! Отсюда возникает приём построения, дающий правильное уменьшение расстояний между последовательными трансверсалями. Построим систему сходящихся в одну точку равноудалённых ортогоналей, и проведём первую трансверсаль, выбрав расстояние от неё до края картины «на глаз»; это построение задаст ближайший к нам ряд квадратов. Теперь проведём в левом квадрате диагональ, уходящую «вдаль и вправо», и продолжим её в этом направлении, чтобы она перечеркнула остальные сходящиеся ортогонали (рис. 24, а). Точки её пересечения с ортогоналями задают положение остальных трансверсалей; проведём и их тоже, чем решим задачу (рис. 24, б).

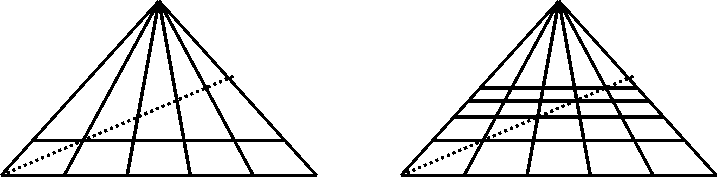
Рис. 24. Построение расчерченного на прямоугольники пола:

(а) проведение первой и второй трансверсалей, задающих направление вспомогательной диагонали; (б) проведение остальных трансверсалей.

Этот приём, несмотря на его кажущуюся простоту, является настоящим геометрическим открытием, и хорошо бы узнать, когда он впервые был применён. Я было подумал, что в соответствии с ним расчерчен пол на картине Коронация девы Марии флорентийского художника Джусто ди Мена-буои, написанной в 1367 году (рис. 25) . Проверка для переднего прямоугольника 8 × 8 дала отменный результат, и казалось, что им можно удовлетвориться; однако такая же проверка для прямоугольника 8 × 8, выделенного на заднем плане, показала, что расстояния между задними трансверсалями заметно завышены. Не думаю, что Джусто размечал параллели на глаз — трансверсали переднего плана для этого проведены слишком точно. Но зачем он тогда раздвинул трансверсали заднего плана?

Рис. 25. Джусто де Менабуои. Коронация девы Марии (нижняя часть). 1367.

Три синих прямых проходят через одну точку, что подтверждает правильность построения трансверсалей переднего плана. Однако три зелёных прямых не проходят через одну точку — трансверсали заднего плана проведены с заметной ошибкой.

Похоже, что действительно правильные прямоугольные сетки, выполненные с построением вспомогательной диагонали, появляются только у художников XV века, занявшихся освоением системы линейной перспективы. И тем более, только в системе линейной перспективы может быть поставлен вопрос о правильной глубине картины. Допустим, что мы умеем правильно построить сетку равноудалённых ортогоналей и трансверсалей. Но как сделать, чтобы это была сетка не каких-то произвольных прямоугольников, но именно квадратов?

Ответ на этот вопрос требует введения совершенного нового принципа организации живописного пространства, сопрягающего иллюзорное изоб-ражёние на картине и свободное пространство перед картиной. Согласно этому принципу, чтобы создаваемое картиной впечатление было верным, зритель должен рассматривать её не с произвольного расстояния, но с некоторой специальной точки, заданной художником в тот самый момент, когда он начал размечать пространство картины. Переход к настоящей линейной перспективе происходит во самом конце первой четверти XV века. По-видимому, первым тут был Мазаччо с его фресками капеллы Бранкаччо (1423–1428) и построенной по всем правилам перспективы Троицей (1427); примерно в это же время было написано Благовещение, ныне приписываемое Уччелло, и ещё одно Благовещение работы Мазолино. Линейная перспектива сделала возможным сколь угодно сильно увеличить глубину изображения, а главное — научила художников рассчитывать эту глубину, чтобы изображённые на картине квадрат и круг с определённой точки зрения действительно выглядели квадратом и кругом, а не прямоугольником и эллипсом.