Физико-химические аспекты процессов пенообразования дисперсными системами пав

Ц елью настоящего исследования является изучение процессов пенообразования¹ и выявление влияния различных свойств пенообразователей ПАВ на эксплуатационные свойства пен. Наименование исследуемых пенообразователей, их возможная предельная концентрация, поверхностное натяжение, интервал рН образования и др. приведены в таблице.

В.Г. КУЛИКОВ Физико-химические аспекты процессов пенообразования дисперсными системами ПАВ

Основные свойства исследуемых пенообразователей

s s sr я в s в ’S' Eh g 4 К О в	Название группы	Наименование	Предельная концентра-ция С пр. , мак.%	Рацио-нальн. концентрация С, мак.%	Поверхн. натяжение σ •10 3 , Дж/м 2	Интервал рН пено-образования	Плотн. пены d , г/л	Коэффициент использования пены, К
I	Алкилсульфаты	ПО №1	2,6	3,0	26,0	2–9	35,0	0,95
		Прогресс	1,7	2,0	28,0		35,0	0,95
		ПО-6К	2,2	2,5	32,0		45,0	0,95
II	Сульфонаты	Сульфанол-40	2,2	2,5	30,5	2–10	40,0	0,9
		Пеностром	2,6	3,0	35,0		50,0	0,95
		ОС	2,2	2,5	37,0		50,0	1,0
III	Производные карбоновых кислот	Квин	6,5	7,0	49,0	6–12	100,0	0,55
IV	Производные смоляных кислот	СДО	9,0	10,0	43,0	6–12	80,0	0,8
		Клееканифольный ПО	5,5	6,0	45,0		65,0	0,9
V	Гидролизаты белков	Неопор	2,4	2,5	54,0	6–10	75,0	0,9
		Унипор	2,8	3,0	54,0		75,0	0,9
		SB-31	2,9	3,0	53,0		80,0	0,9
		ГК	2,5	3,0	53,0		80,0	0,9

Пены, как дисперсные системы, перечень и основные свойства которых приведены в таблице, получали в процессе испытаний методами диспергирования посредством перемешивания. Помимо этого, как отдельный прием, применялся конденсационный метод, основанный на изменении физического состояния раствора ПАВ путем повышения температуры2 при постоянном внешнем давлении, приводящем к пересыщению раствора газом.

Обозначим основные факторы влияющие на процессы пенообра-зования. Ими, на наш взгляд, являются поверхностное натяжение ( σ )

В.Г. КУЛИКОВ Физико-химические аспекты процессов пенообразования дисперсными системами ПАВ и характеристики кинематической η и динамической µ вязкости исследуемых дисперсных сред. Установлено, что образование дополнительной поверхности, происходящее при вспенивании, тем вероятнее, чем меньше работа, которую необходимо затратить на образование этой поверхности (т. е., чем меньше поверхностное натяжение на границе раздела дисперсных фаз с газом).

Тем не менее, если бы решающее значение имели только эти физические свойства, то поверхностно-активные вещества с небольшим поверхностным натяжением обладали бы б ó льшей способностью к вспениванию, чем ПАВ с высоким поверхностным натяжением. Однако многие ПАВ с низким поверхностным натяжением как, например, спирты и эфиры, не образуют пены, в то время как другие, с относительно высоким поверхностным натяжением, легко вспениваются.

Аналогичное наблюдается и в отношении вязкости. Так, некоторые вязкие ПАВ сами по себе не образовывают пены, в то время как иные ПАВ с небольшими коэффициентами вязкости дают обильную пену. Таким образом, ни вязкость, ни низкое поверхностное натяжение не являются универсально-решающими факторами, определяющими явления вспенивания.

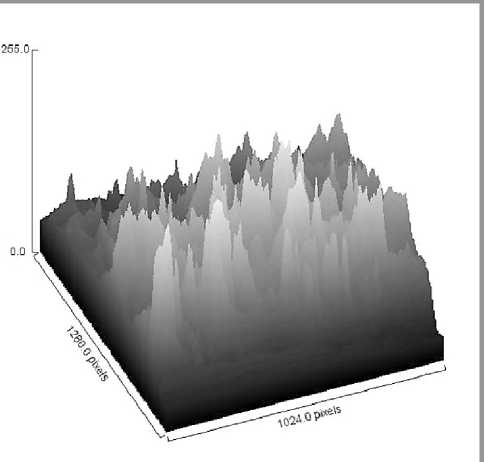
В процессе исследований выявлено, что первой стадией процесса пенообразования являлось образование газовой эмульсии, т.е. образование системы газ-раствор ПАВ , а также появление на межфазной поверхности адсорбционных слоев-пленок ПАВ, изображенных на рис.1.

Процесс накопления молекул ПАВ отчетливо просматривается в виде контурных линий граней выпуклых полиэдрических многоугольников структуры пены

Рис. 1. Первичная стадия процесса образования пены полиэдрическими по форме элементарными ячейками пены с отчетливо выраженным процессом адсорбции молекул ПАВ на поверхностях газовоздушных пузырьков

В.Г. КУЛИКОВ Физико-химические аспекты процессов пенообразования дисперсными системами ПАВ

Отметим, что форма элементарных ячеек пен ( «паркет» ) из-за меняющейся поверхностной энергии ( σ ) дисперсной системы существенно зависела от соотношения объемов газовой и жидкой фаз пенообразователей и, в зависимости от этого отношения, принимала:

• 1)    либо полиэдрическую форму ячеек, представленную на рис. 1;

• 2)    либо сферическую форму ячеек, схематически изображенную на рис. 2, в структуре которой отчетливо прослеживался ближний и дальний порядок;

• 3)    либо переходную (многогранную) ячеистую структуру, представленную на рис. 3.

  б

  
  

  а, б - схематичное представление дипольных молекул ПАВ

  
  
  

  Схема углеводородной цепи

  с радикальными группами молекул ПАВ

  
  
  

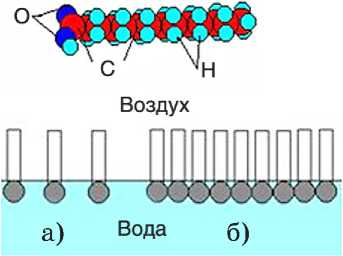
  Адсорбционная пленка ПАВ на пленке эмульсии

  
  
  

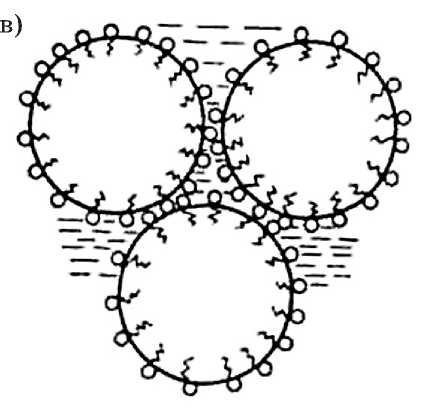
• а)    разреженная адсорбция молекул ПАВ, существенно не изменяющая поверхностную энергию жидкости раствора;

• б)    плотная адсорбция молекул ПАВ, существенно уменьшающая поверхностную энергию жидкости раствора;

• в)    схема процесса образования плотной шаровой упаковки пен, обладающих ближним и дальним порядком

Рис. 2. Схема процесса пенообразования молекулярными группами ПАВ

В.Г. КУЛИКОВ Физико-химические аспекты процессов пенообразования дисперсными системами ПАВ

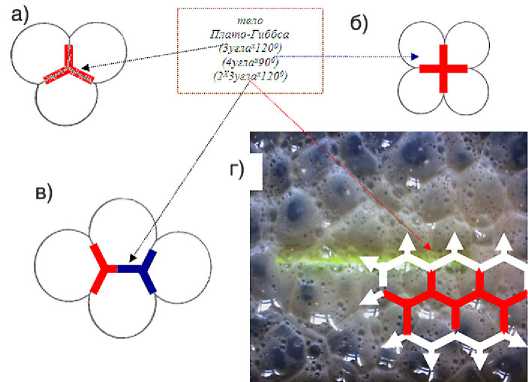
Условия формирования геометрических форм устойчивых континуальных сплошных пенных сред:

а) многогранная плоская зона контакта 3 ячеек с углами 120о;

б) неустойчивое состояние 4 пленок с углами 90о;

в) устойчивое состояние 4 пленок с углами 120о;

г) мономодальная дисперсная среда с углами 120о

Рис. 3. Схема превращения неустойчивых дисперсных пен в устойчивые

Во всех случаях наблюдения структуры пен обладали самоподобными орнаментами, своеобразными «паркетами». Структуры без ближнего или дальнего порядков не наблюдались.

Предложим гипотезу о механизмах и движущих силах, влияющих на изменения формы ячеек пен. Наиболее вероятная форма структуры элементарных ячеек формирующихся пен может быть обоснована тем, что газовоздушные пузырьки пен, пленки которых встречаются под углами 120о, создают уравновешенную устойчивую систему, показанную на рис. 3.

При соединении, т. е. «схлопывании» пузырьков, пленки, разделяющие пузырьки в плоскости, преобразовываются в трехугольный «моностолб» жидкости, который циркулирует в разветвленных каналах Плато-Гиббса. Именно этот «моностолб» и является пространственным контуром пленок пен, т. е их несущим остовом. Именно он и пленки, как бы натянутые на него как на пространственный стержневой каркас,

В.Г. КУЛИКОВ Физико-химические аспекты процессов пенообразования дисперсными системами ПАВ разделяют внутренние и внешние пространства дисперсных фаз от среды растворов ПАВ, одновременно образовывая межслоевые «жгутовостолбовые» цепи-щели.

Известно, что величина избыточного давления в газовоздушных пузырьках дисперсных сред определяется величиной поверхностной энергии ( σ ) пленок и двоякой кривизной газовоздушных пленок. Таким образом, двоякая кривизна сама по себе является причиной перепада давлений ∆ р в ячейках, т. е. между газовой и жидкой фазами:

∆р = σ•(Ri + R2 ), где σ – поверхностная энергия дисперсной системы; R1,2 - радиусы кривизны двух взаимно перпендикулярных нормальных сечений поверхности пленки. Считается, что радиус кривизны положителен, если ее центр находится внутри пленки (выпуклый мениск), и отрицателен, если центр кривизны вне пленки (вогнутый мениск).

Следовательно, жидкость, в зависимости от знака разности указанных давлений, принципиально может перетекать из пленки в обозначенный нами жгутовый канал Плато-Гиббса и, таким образом, утонять пленку, истекая из нее, но утолщая жгутовый канал. Устойчивость дисперсной пенной системы в этом случае обеспечивается увеличивающейся жесткостью пространственной структуры каналов-жгутов, представляющих собой развитую капиллярную наноструктуру. Либо наоборот, течь из канала в пленку, таким образом утолщая ее3, но при этом утоняя жгутовый канал. В этом случае устойчивость дисперсной пенной системы обеспечивается увеличивающейся жесткостью пенных пленок, представляющих собой своеобразный жесткий пространственный ячеисто-паркетный каркас.

Принято считать толщины стенок пенных пузырьков постоянными и сопоставимыми по размерам с размерами самих молекул ПАВ. Исходя из этих соображений очевидно, что существенные «перетоки туда-сюда» из-за незначительных толщин пленок и жгутов-каналов без их обоюдного разрушения маловероятны, хотя потенциально возможны.

В.Г. КУЛИКОВ Физико-химические аспекты процессов пенообразования дисперсными системами ПАВ

Но вполне вероятно, что все-таки подобные процессы имеют место, давая о себе знать нарушениями дальних порядков наблюдаемых структур пен. Мы же этот факт можем зафиксировать, наблюдая в реалиях двойные, тройные и прочие «арные» орнаменты паркетов пен.

Таким образом, наблюдая в натуре нарушения орнаментов пен, можно предположить, что дисперсная система, представляя собой само-регулируемую структуру, в этот момент не находится в равновесии. Тем не менее, значительных отклонений от равновесия дисперсные пенные системы не допускают, своевременно запуская механизм торможения перетока, что, по всей видимости, и происходит в действительности. Каким образом система стабилизируется? Так как в изучаемых системах σ ≠ 0 , то равенство ( ∆ р = 0) возможно только если:

(R+ r ) = 0, откуда R= – R₂ , значит R₁ = –R₂.

Последнее выражение явно указывает на путь, которым необходимо идти для выравнивания давлений. Центры кривизны R1 и R2 должны находиться по разные стороны от пленки, создавая плоский мениск. На наш взгляд, именно в этом и заключается механизм торможения перетоков и стабилизации структур пен.

Анализируя вышесказанное, можно с уверенностью предсказать форму элементарной ячейки пены, как наиболее вероятную, т. е. форму, исключающую наличие перепада вышеуказанного (Лапласового) давления и, кстати, очень часто применяемую природой самой пены. Такая ячейка может представлять собой только энергетически сбалансированные 5 форм Платоновых тел или с небольшими отклонениями 12 выпуклых неправильных многогранников. Таким образом, количество элементарных форм паркета пен, собственно, и наблюдается в процессе исследований. На наш взгляд, это положение о счетности и конечности множества форм элементарных ячеек является определяющим для обоснования наличия ближних порядков структур пен. Безусловно, при преобладании по разным причинам в системе деструктивных процессов происходит нарушение высказанного положения и, следовательно, нарушение в начале дальнего, а затем и ближнего порядков, т. е. разрушение системы.

В настоящей работе представим элементарную форму паркета пены только одной формой - додекаэдром, ограниченным 12 пятиугольными

В.Г. КУЛИКОВ Физико-химические аспекты процессов пенообразования дисперсными системами ПАВ гранями (рис. 4). Такое представление формы элементарной ячейки позволяет установить аналитические зависимости между геометрическими [площади боковых поверхностей (Sбок), объемы тел (Vтела ) и др.], энергетическими [поверхностная энергия (σ), потенциал Гиббса ( de ), где с – концентрация ПАВ в растворе, энергия образования дополнительной поверхности и др.], а также и другими инженерными характеристиками у различных видов пенных структур.

Полиэдрическое строение ячеек

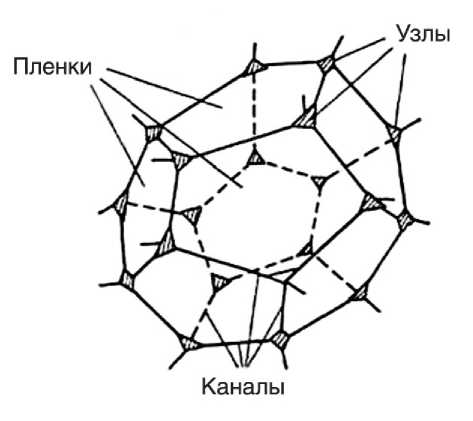
Рис. 4. Энергонейтральная элементарная форма ячейки дисперсных пен - додекаэдр

ВЫВОД.

• 1)    Подчеркнем, что поверхности пенных пленок в виде Платоновых тел не имеют кривизны. Следовательно, состояние такой пенной структуры, как дисперсной системы, равновесно.

• 2)    Пены с такой, в том числе додекаэдрической структурой, устойчивы.

• 3)    Ближний и дальний порядок структур пен с элементарной полиэдрической ячейкой отчетливо выявлены и подтверждены в процессе исследований. Они приведены на рис. 1, 2, 3.

В.Г. КУЛИКОВ Физико-химические аспекты процессов пенообразования дисперсными системами ПАВ

Установлено, что пены кратностью выше 4 характеризовались по-лифракционной сферической пористой структурой и возрастающим количеством соприкасающихся пор по мере роста показателя кратности. Теоретическому пределу такой плотной упаковки структуры соответствует пористость в 83% и кратность, равная 6.

Пеноматериалы при сухой минерализации, т. е. при добавлении расчетных доз сухого порошка минерального вяжущего, после отвердевания приобретали открытую пористость за счет наличия точечных «дырок» в зоне соприкосновения сферических пузырьков пены. Это хорошо видно на рис. 5.

Фрагмент внутренней структуры пеноматериала, образованный пеной. Отчетливо проявлена пузырьково-сферическая форма и наличие дырок в пленках

Рис. 5. Пузырьково-ячеистая структура пены ПАВ

Пены кратностью 9 ^ 14 обладали объёмом воздушной фазы 89 ^ 93%. Они могут служить основой (при В/Т = 0,5 ^ 0,6) для получения особо легких (150 ^ 250 кг/м³) пено- теплоизоляционно-конструкционных материалов на обычном цементном вяжущем.

Увеличение воздушной фазы в пенах кратностью выше 6 приводило к постепенному ухудшению их свойств за счет перестройки структуры в плотную и жесткую упаковку частично деформированных сферических пузырьков в зонах соприкосновения сфер.

В.Г. КУЛИКОВ Физико-химические аспекты процессов пенообразования дисперсными системами ПАВ

Самыми низкими показателями стойкости обладали пены кратностью выше 9.

При флокуляции пузырьков на поверхности растворов ПАВ образовывался связный пленочный каркас, представляющий собой единую пенную структуру (см. рис. 5, 6).

След секущей плоскости, в которой выявлен фрактал поверхностной линии пенной пленки ПАВ

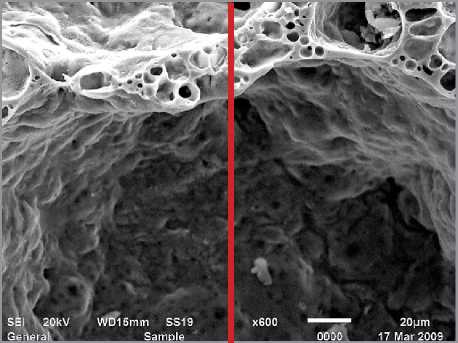
Фракталы поверхностной линии пенной пленки ПАВ по вышеуказанной линии

Расстояние (мкм)

Рис. 6. Определение толщины пенной пленки СДО + канифольный клей

Сфероподобная пена образовывалась в тех случаях, когда объем жидкой фазы ( V_ж ) превышал объем газовой фазы ( V_г ) более чем в 10 ^ 15 раз. Установлено, что чем меньше отношение ( V / V) ), т. е., чем больше образовывалось газовой фазы при постоянном объеме жидкой, тем меньшее значение принимала толщина пенной пленки. Как видно

В.Г. КУЛИКОВ Физико-химические аспекты процессов пенообразования дисперсными системами ПАВ из рис. 6, толщина пленки колебалась в интервалах ~10^50 мкм. Указанный размер эквивалентен (1^10-5^5^10-5) м = (1*10+4^5*10+4) нм, т. е. ~ (10000^50000) нм, который не может быть отнесен к категории наноразмеров. Процесс определения указанных размеров и пояснения приведены на рис. 6.

Тем не менее, рассматривая всю толщину пленки как множество, не относящееся к категории нано- структур, отметим, что в самой пленке происходят ранее указанные процессы, носителями которых являются молекулы и другие структуры ПАВ. Оценивая их категорию размеров в ~(1•10–7) м ≡ (1•10+2) нм, которые уже могут быть соотнесены с категориями наноразмеров, вычислим количественный порядок указанных структур, считая их собственными элементами вышеуказанного множества, т. е. подмножествами. Их мощность составляет:

|; ^ - | *. 1Q+2 ^1 •¹⁰⁺²- ⁵ •^{1Q 2= 100} - ⁵⁰⁰ единиц -> \М\.

Зная общую протяженность пенных пленок (lпл) и полученную мощность ПАВ, приходящиеся на их единицу длины, предлагаем метод расчета параметров пенных пленок пенообразователей ПАВ в виде параметрического подбора при известных любых двух из вышеуказанных трех параметров соотношением:

P по = | М |• l

пл

где ( P_по ) – общий расход пенообразователя ПАВ.

Предлагаемый метод применим и в случаях, когда из вышеприве- денных параметров известен лишь один. Задаваясь значениями неизвестных параметров и соблюдая приведенное соотношение, получали результаты, значительно превосходящие по точности известные экспериментальные методы.

С течением времени пленки все более утонялись и сфероподобная пена превращалась в полиэдрическую.

В процессе изучения поведения таких структур пен были уточнены показатели их седиментационной и агрегативной устойчивости. Однако, по мере превращения сферо-подобной пены в связную полиэдрическую, понятие седиментационной устойчивости применительно к ней теряло физический смысл.

Агрегативной устойчивости изучаемых пен поставлена в соответствие скорость укрупнения частиц дисперсной фазы за счет коалесценции и из-за других процессов перестройки структуры.

В.Г. КУЛИКОВ Физико-химические аспекты процессов пенообразования дисперсными системами ПАВ

Стабилизация изучаемых пен осуществлялась следующими способами:

• 1)    с помощью применения различных типов ПАВ, приведенных в таблице;

• 2)    путем введения в пену рационально подобранных количеств мелкодисперсных керамзитных высевок;

• 3)    добавлением в пену небольших доз сухого порошка минерального вяжущего.

ВЫВОД.

На наш взгляд, в зависимости от природы ПАВ и свойств образуемых ими адсорбционных слоев, устойчивость пен обуславалась действием общих для дисперсных систем факторов стабилизации, таких как: 1) ионно-электростатические; 2) структурно-механические барьеры; 3) специфический для пен и эмульсий эффект Гиббса-Марангони.

Эффект Гиббса-Марангони в наших исследованиях заключался в следующем. Течение жидкости в поверхностных слоях пенных пленок приводило к уносу из них ПАВ и, следовательно, к увеличению поверхностного натяжения ( σ ). Этот процесс вызывал возникновение давления, двунаправленного и направленного в сторону, обратную истечению жидкости (эффект Марангони). Одновременно с этим, увеличение ( σ ) приводило к повышению упругости пленки, препятствуя ее механической деформации (эффект Гиббса). Отсюда следует, что в присутствии ПАВ утонение пленок может происходить только путем вытекания жидкости между адсорбционными слоями ПАВ.

ВЫВОД.

При небольших значениях толщин зазоров этот процесс идет с небольшой скоростью и, следовательно, управляя скоростью процесса утонения (т. е. скоростью истечения), можно обеспечивать необходимую устойчивость пен. Безусловно, при этом необходимо учитывать и другие стабилизирующие процессы. Это, например, процессы, связанные с гидратацией вяжущего, начинающиеся с момента его затворения.

Для проверки высказанной гипотезы о механизмах устойчивости пенных пленок был проведен эксперимент по определению равновесного капиллярного давления в каналах Плато-Гиббса, зависящий от высоты столба пены h следующим образом:

pσ = pL ± ρ•g•h, где pσ - давление в нижнем слое пены; ρ - плотность раствора ПАВ.

В.Г. КУЛИКОВ Физико-химические аспекты процессов пенообразования дисперсными системами ПАВ

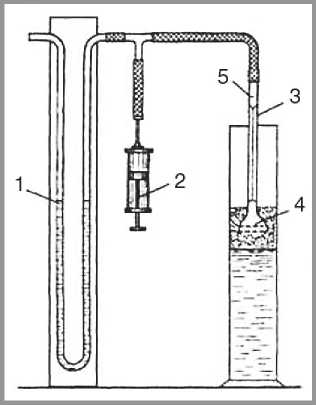
Рис. 7. Установка для определения равновесного давления в каналах Плато-Гиббса

Капиллярное давление измеряли с помощью установки, изображенной на рис. 7. Установка состояла из U-образного водяного манометра 1, цилиндра с поршнем 2 (шприца) и капиллярной трубки 3 с приваренной пористой мембраной 4. На трубке 3 на высоте 10 см от мембраны нанесена метка 5.

Измерения производили следующим образом. Трубку 3 опускали в стакан с раствором ПАВ на глубину 0,2 : 0,5 см и при помощи поршня 2 уровень мениска раствора в капиллярной трубке 3 совмещали с меткой 5. Значение пониженного давления, фиксируемое манометром 1, принималось за начальный отсчет р₀ . Затем емкость с раствором ПАВ заменяли емкостью с пеной и трубку 3 опускали в пену на глубину 1 см. При соприкосновении с пеной, из-за пониженного давления в пенных каналах, жидкость стремилась перейти из трубки 3 в пену. Поэтому мениск жидкости в трубке 1 опускался. Перемещая поршень 2, создавали дополнительное разрежение над мениском, добиваясь, чтобы жидкость из капилляра не вытекала в пену, но при этом и не отсасывалась из нее. Именно это давление р_L и регистрировалось по манометру 1. Равновесное капиллярное давление находили как разность давлений р_L и p₀ .

ВЫВОД.

Из анализа высказанных гипотез и экспериментальных данных, приведенных на рис.1, 3, 5 и 6, следует:

О пенные структуры по их размерам можно отнести к наноструктурам, т. к. они фрактальны, обладают собственным паркетом ближнего и дальнего порядка и имеют размеры подэлементов порядка 10 : 200 нм;

О экспериментальными данными (рис. 5, 6) подтверждена фрактально-кластерная автомодальная форма строения структуры указанных пен.

В проведенных исследованиях использованы положения фрактально-кластерного исчисления. На рис. 8 а, б приведена общая схема фрак-                           к содержанию

В.Г. КУЛИКОВ Физико-химические аспекты процессов пенообразования дисперсными системами ПАВ тально-кластерного анализа паркетов «автомодольности» пен и их обоснование для правил вывода ближнего и дальнего порядка.

а)

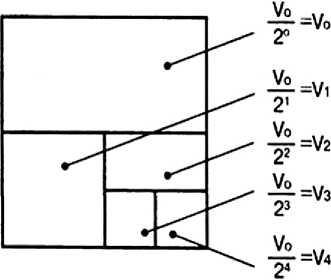
б)

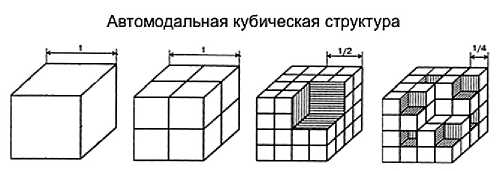
Рис. 8. Фрактально-кластерное представление паркетов пен как обоснование наличия ближнего и дальнего порядков пен

Представим структуры примитивных форм множеств пен соответствующими подмножествами ближних и дальних порядков по следующей схеме. Примем общий объем всей пены за множество объемом V₀ . Подмножествами данного множества в виде элементов дальнего и ближнего порядков будем считать его элементы паркета и заполнять его общий объем объемами элементов паркета по следующей схеме.

Первым подмножеством, как первым паркетом, заполним половину общего объема V₀ , т. е. V₁ = 0,5• V₀ .

Вторым паркетом заполним половину оставшегося объема V₂ = 0,5•( V₀ –0,5• V₀ ) = 0,25• V₀ . Объем третьего паркета определим как V₃ = 0,5•( V₀ –0,5• V₀ –0,25• V₀ ) = 0,125• V₀ .

Общая схема заполнения объема пены V₀ паркетами V_j приведена на рис. 8 а. Такого рода действиями поставим в соответствие степень заполнения ( С_зап ) общего объема ( V₀ ) пены степенью востребованности ( С_востр ) паркетов ( Σ V_j ) и количественно оценим степень наличия ближних и дальних порядков паркетов пены, представив высказанное утверждение аналитически как ( С_зап ) = f (C^ )}.

Тогда, если {( С_зап ) = f ( ^в остр )} ^з , ^{а п} то { f ( ^востр ) → lim_{n →∞} f ( ^востр ) → 0 ≡ ближний порядок пены}.

В.Г. КУЛИКОВ Физико-химические аспекты процессов пенообразования дисперсными системами ПАВ

Иначе { f (    ) → lim   f (    ) → ± ∞ ≡                                 }.

n →∞

Как уже ранее отмечалось, исследуемые пенные структуры представляют собой фрактальные системы (рис. 1, 3, 5, 6). Произведем анализ указанных фрактальных систем, используя параметры кубической сингонии (кубическая упаковка с линейным параметром а0 = 1) (см. рис. 8 б). Введем следующие обозначения. Количество рассматриваемых объектов (фракталов) обозначим как {       }. Этому показа телю можно поставить в соответствие, как множество, собственно саму пену {П ≡ пена}. Общий объем (мощность) этого множества составляет |V0|. Мощность элементов {паркетов} множества {П} обозначим через {     } и представим их как геометрические объекты, подобные по фор ме самим себе, но отличающиеся друг от друга масштабом представления, т. е. как самоподобные множества (рис. 8 а).

Для кубической упаковки {       } = 1 т. к. на первом этапе нами рассматривается один объект. Это куб с единичной стороной, линейный параметр которого а0 = 1. При уменьшении линейного параметра данного объекта в два раза он образует восемь самоподобных множеств {паркетов}, значит [{      } = 8]. Величину [{      } – {        }] = [ ]

примем за основание показателя рекурсии выше обозначенных самоподобных множеств и обозначим как [ ] . В силу того, что нижеприведенные инструкции могут выполняться неограниченное количество раз, повторяя одни и те же действия с различными исходными данными, пронумеруем их, обозначив как {№ (итер) = 0 ^^ }. Тогда алгебру обращений, как носитель и сигнатуру рекурсии в виде [ n^x_y ≡ y^x ] к рассматриваемому множеству, можно представить в виде выражения сочетаний из [ ] по [{№ (итер)}] в виде следующего выражения:

Гп [{№ (итер)}]                         _ Г 1 [{№ (итер)}] 1

L //^равных!— J ^количество № (итер)+11 _ г0П-|\

• 1    фигур ’ фракталов’

Раздробим виртуально исходный куб на восемь равных кубов со стороной, равной а₁ = 0,5• а₀ . Номер итерации данной инструкции равен 0, т. е. [{№ (итер)}] = 0. Тогда [{      } = 8]; [ n^x_y ≡ y^x ] →

→→

→→ фигур        фракталов                    р_

Из этого следует, что рассматривается один фрактальный объект, и этим объектом является сам единичный куб.

В.Г. КУЛИКОВ Физико-химические аспекты процессов пенообразования дисперсными системами ПАВ

Отбросим один из восьми объектов, представляя этот объект как количество рекурсивных обращений на этом этапе (т. е. количество отбрасываемых объектов на этом этапе является величиной [n;«i _ ,<трт>1из предыдущего этапа), а остальные семь из оставшихся вновь раздробим на восемь равных частей. Это итерация №1, т.е. [{№ (итер)}] = 1. Основание показателя рекурсии [Op] = 7, так как №ф"У} H{^X^ 2 }] ↔ [{8} – {12}] = 7. Тогда новых фрак-L1 фигур J 11 фракталов 1 J тальных объектов уже будет: [Op]•{^равных} → 7•8 = 56 со стороной а2 = 0,5•а1 = 0,25•а0. Отсюда количество обращений на этой итерации [n^-^i-T^r^J^-T. Продолжим вышеобозначенные действия.

Определим количество новых фрактальных объектов для следующего этапа: [ Op]•{"^фигур } → [56–7]•8 = 392 со стороной а₂ = 0,5• а₁ = 0,25• а₀ . Это итерация №2, т. е. [{№ (итер)}] = 2. Основание показателя рекурсии [ °p ] как [{KP™™} {{^фракталов°^ " ^ ↔ [{392} – {7³}] = 7. Отсюда количество обращений на этой итерации[“b-^^⁷!^⁴⁹.

Рассуждения для расчетов единичного куба можно представить следующей схемой:

[{a0^(l)° = [{а.^ф1-[{а2^ф2 = Цап->фп =

Jg = 1)] o [{n°} ^ 7»]; ^lil^tin;)^?1]; ^ j}] <^ [{n2} -> 72];

2" = 2" ^ ^ ['¹¹t¹' ^ 7"J

Из этих соображений следует, что масштабным элементом выступает величина (1/2). Обозначим эту величину Z как коэффициент «автомодальности». Представив в соответствии с [7] фракталь- ln[[O"]]               ln[7]

ную размерность как d =----, получим ln2 = 2,807.

lnz

Численное значение размерности показывает, что такой фрактал кубической упаковки пенных паркетов есть нечто среднее между поверхностью и пространственным образованием, поскольку 2

В.Г. КУЛИКОВ Физико-химические аспекты процессов пенообразования дисперсными системами ПАВ

При имитационном моделировании структур пен необходимо принимать во внимание следующие положения:

• 1)    вытекание жидкости из пленок происходит под действием сил капиллярного всасывания, которые в 20-25 раз превосходят гравитационные силы. Поэтому характерное время перетекания жидкости из пленок в каналы занимает значительно меньше времени, чем процесс истечения жидкости из пен;

• 2)    скорость течения жидкости по пленкам, имеющим размеры, характерные для реальных пен, намного меньше скорости перемещения жидкости по пенным каналам.

ВЫВОД.

Моделью, которая может адекватно описывать синерезис пен, следует считать капиллярную (каналовую) модель (рис. 9), в которой истечение жидкости происходит из системы вертикальных каналов4, протяженных на всю высоту пенного столба.

б)

Рис. 9. Капиллярно-каналовая модель пены и ее графо-аналитическое представление:

• а)    капиллярно-каналовая модель пены;

• б)    графо-аналитическое представление модели пены

В.Г. КУЛИКОВ Физико-химические аспекты процессов пенообразования дисперсными системами ПАВ

Чистые жидкости вспенить не удается, т. к. их пленки мгновенно разрушаются. При этом скорость протекания по всем каналам одинакова и газожидкостная смесь представляет собой сеть параллельных каналов релаксации.

Реальное имитационное фрактально-кластерное моделирование процессов образования форм структур пен на основе предлагаемой автором методики позволяет осуществлять интерактивный процесс контроля формирования пенных структур в режиме реального времени.