Определение молекулярной массы, размера и разветвленности макромолекул с помощью двухдетекторной ГПХ. Использование ГПХ с рефрактометрическим детектором и многоугловым лазерным нефелометром (Malls)
Автор: Беленький Б.Г.
Журнал: Научное приборостроение @nauchnoe-priborostroenie
Рубрика: Обзоры
Статья в выпуске: 1 т.11, 2001 года.
Бесплатный доступ
Важнейшим видом анализа полидисперсности полимеров является гель-проникающая хроматография (ГПХ) как метод определения их молекулярно-массового распределения (ММР). Рассмотрены виды ГПХ-анализа и их применение в исследовании полимеров.
Короткий адрес: https://sciup.org/14264162
IDR: 14264162 | УДК: 543.544:
Текст научной статьи Определение молекулярной массы, размера и разветвленности макромолекул с помощью двухдетекторной ГПХ. Использование ГПХ с рефрактометрическим детектором и многоугловым лазерным нефелометром (Malls)
Молекулярные характеристики полимеров: молекулярно-массовое распределение (распределение по молекулярным массам макромолекул М ), разветвленность (распределение по типам разветвленности), композиционная неоднородность (распределение по химическому составу гетерополимеров), функциональность олигомеров (распределение по типам функциональности) — играют важнейшую роль в химии, физике и технологии высокомолекулярных веществ. С одной стороны, эти характеристики позволяют судить о процессах полимеризации, сертифицировать полимерные материалы, с другой — прогнозировать технические характеристики полимерных изделий, получаемых при переработке полимерных материалов, определять оптимальные условия этой переработки.
Важнейшим видом анализа полидисперсности полимеров является гель-проникающая (эксклюзионная, size-exlusion) хроматография ГПХ (GPC) [1] как метод определения их молекулярномассового распределения (ММР). Здесь наибольшие достижения связаны с колоночной двухдетекторной ГПХ, где колонка с макропористым сорбентом используется для фракционирования макромолекул по размеру, а переход от размера макромолекул к их М связан с использованием уравнения Бенуа:
V R = A - B ln( M [ ^ ]). (1)
Здесь V R — удерживаемый объем, [ п ] — коэффициент динамической вязкости. Если знать параметры ( к п , a ) уравнения Марка—Куна
[ П ] = k n M a , (2)
то этот переход несложен:
V R = A - B In k n - B ( a + 1)ln M = C - D In M . (3)
Здесь коэффициенты А и В определяют из универсальной калибровочной зависимости ГПХ (1), полученной по узкодисперсным полимерным стандартам (чаще всего полистирольным) с известными М и коэффициентами k n и аВ при применяемом для ГПХ растворителе. С и D — коэффициенты рабочей калибровки ГПХ, которая может быть получена непосредственно, если использовать полимерные стандарты с известным ММР.
Используя в качестве детекторов для ГПХ, наряду с проточным рефрактометром (для определения весовой концентрации), проточный вискозиметр (для определения [ п ]), можно определить ММР полимера при отсутствии его стандартов и при неизвестных константах Марка—Куна в использованном для ГПХ растворителе. При этой процедуре определяются также К п и а для исследуемой системы полимер—растворитель, если известно ММР полимера.
Более простая процедура определения ММР неизвестного полимера получается при использовании комбинации ГПХ с рефрактометром и многоугловым лазерным нефелометром (Multiangle Laser Light Scattering Photometer — MALLS) [2]. Этот метод позволяет определить не только ММР полимера, но и распределение по размерам, а в случае разветвленного полимера — идентифицировать его разветвленность. Новые возможности анализа полимеров представляют сочетание ГПХ (с рефрактометрическим детектором) и Matrix Lazer Desorption and Matrix Assisted Laser Desorption/Ionisation MassSpectrometry — MALDI MS [3]. Эта техника позволяет определять М и структурные особенности фракционируемых макромолекул.
Все эти возможности связаны с использованием дорогостоящей техники, которая однако не обеспечивает фракционирование макромолекул, различающихся по химической структуре, но идентичных по размеру.
Здесь полезно использовать не ГПХ, а другие виды хроматографии, например адсорбционную, особенно удачно реализуемую в тонкослойном варианте [4].
Эти виды хроматографии можно рассматривать как "неидеальную" ГПХ, отличающуюся от "идеальной" ГПХ, при которой удерживаемый объем зависит только от соотношения размеров макромолекул ( R ) и размеров пор ( r ):
V r = V r ( RI r ). (4)
Уравнение (4) может быть названо уравнением Касаса (Cassasa) [1], предсказавшего теоретически эту универсальную зависимость. Зависимость Касаса (4) отличается от зависимости Бенуа (1) своей универсальностью, поскольку она справедлива для любого макропористого сорбента, в то время как зависимость (1) можно использовать только для сорбента со строго определенным распределением пор по размеру.
Развитие представлений о "неидеальной" ГПХ, открытие соответствующих законов и использование "неидеальной" ГПХ в анализе полимеров с помощью тонкослойной хроматографии (ТСХ) и колоночной хроматографии были сделаны в наших работах, выполненных в ИВС АН СССР [5].
Первая проблема — это ГПХ гигантских макромолекул (с М > 5406 Да), где существенную роль играют следующие обстоятельства:
— Необходимость использования гигапори-стых сорбентов, через поры которых протекает поток элюента, что приводит к
-
■ уменьшению на величину протекаемого объема пор и
-
■ к деструкции макромолекул, перемещающихся в каналах сорбента.
— Необходимость увеличения размеров зерен сорбента (который должен быть в 5-10 раз больше диаметра пор). Последнее ведет к
-
■ увеличению сопротивления массопере-даче (пропорционального квадрату диаметра зерна сорбента) и
-
■ сильной неравновесности ГПХ, приводящей к зависимости V R от скорости элюции. Все это кладет естественный предел М макромолекул, доступных для ГПХ ( М < 5406 - 107 Да).
Вторая проблема — это ГПХ при адсорбционном взаимодействии макромолекул с поверхностью пор сорбента [5]. При этом энергия адсорбционного взаимодействия макромолекулярного сегмента со стенкой пор ( - £ ) может варьировать от - £ = -” , когда пристеночный слой растворителя (толщиной в один сегмент) недоступен для сегментов макромолекулы, до - £ = +“ , при которой наблюдается необратимая адсорбция. Можно выбрать (и в принципе рассчитать) критическую энергию - £ = -£ cr , при которой для макромолекулярного сегмента термодинамически безразлично где находиться: в объеме пор или в пристеночном слое. В этих условиях переход макромолекулы из межчастичного объема в поры сорбента не связан с изменением свободной энергии Гиббса ( - A G = 0), и поскольку при изменении - £ состояние - A G = 0 наступает у макромолекулы любой М одновременно ( - £ cr не зависит от М), то ГПХ при - £ = -£ cr не фракционирует макромоле -кулы по М (размеру). Измеренный в этих условиях хроматографический коэффициент распределения ln k d = ln( V p I V 0 ), где V p и V 0 — объемы пор и межчастичного пространства, позволяет определить отношение V p I V 0 :
-
k d ( - £ = -£ cr ) = V p I V ) . (5)
Таким образом, измеренный хроматографически в критических условиях kd может быть использован для определения V p I V 0 слоя сорбента, а следовательно, и геометрического размера пор Vp ( r ) . Характерно, что
V p ( -8 = —) < V p ( -8 = 0) <
< V p ( -8 = -8 cr ) < V p ( -8 > -8 cr )
При - 8 = -8 cr , когда макромолекулы не фракционируются по М , они как бы являются "хроматографическими невидимками". При - 8 > -8 cr мы наблюдаем переход к адсорбционной хроматографии, когда - A G > 0 .
Так, в зависимости от величины - 8 наблюдается три вида хроматографии:
-
■ ГПХ при
- 8 (|-^.-8cr ], (-AG < 0);
-
■ адсорбционная при
-8 ( [- 8cr, +”],(-AG > 0);
-
■ критическая при
-
- 8 =-8cr ,(-AG = 0) •
-
2. ИСПОЛЬЗОВАНИЕ ДВУХДЕТЕКТОРНОЙ ГПХ С КОНЦЕНТРАЦИОННЫМ ДЕТЕКТОРОМ (РЕФРАКТОМЕТРОМ) И МНОГОУГЛОВЫМ ДЕТЕКТОРОМ СВЕТОРАССЕЯНИЯ
В первом случае имеет место монотонное убывание k d от числа сегментов N ( M) макромолекулы ( д k d / д N < 0), во втором случае монотонное возрастание k d от N ( M ) — ( д k d / д N > 0), в критических условиях k d = 1 для всех М . Переход макромолекулы от отрицательной адсорбции к неограниченной адсорбции в точке - 8 = -8 cr - 0 представляет фазовый переход первого рода с характерными для него явлениями: резким изменением знака -A G (при достаточно большом N ), коллапсе размеров макромолекулы. У гетерополимеров (блок- и привитых сополимеров, функциональных олигомеров) можно поставить в критические условия "хроматографической невидимки" одну из частей макромолекулы и определить ММР ее "видимой" части — одного из блоков, ветвей или основы привитого сополимера, функциональных групп олигомеров. Практически выгодно работать в следующих энергетических областях хроматографии: - 8 ^ -^ (ГПХ), - 8 = -8 cr - 0 (докрити-ческие условия), - 8 = -8 cr + 0 (околокритические условия), - 8 = -8 cr (критические условия). Док-ритические и околокритические условия можно использовать для фракционирования олигомеров по М отдельно для каждого типа функциональности, а критические условия — для фракционирования сополимеров по М одной его части, в то время как другая часть (части) является "хроматографической невидимкой". Последнее возможно потому, что Гиббсова свободная энергия - A G представляет сумму его частей - A G i .
Третья проблема неидеальной ГПХ связана с отклонением от идеальности вследствие концен- трационных эффектов — относительно небольших у обычных полимеров из-за уменьшения их размеров при увеличении концентрации и значительных при связанной с увеличением концентрации ассоциации макромолекул, подавления полиэлектро-литного набухания, вязкостными эффектами, вызывающими деформацию и разрушение границ полимерных зон.
Последний эффект может моделировать прорыв воды через вязкий нефтяной слой в пористой среде при законтурном обводнении нефтяных скважин. С другой стороны, этот феномен может быть использован для определения хроматографической вязкости полимера из ТСХ-эксперимента [4].
Вопрос интерпретации данных ГПХ — это прежде всего вопрос получения скорректированной на хроматографическое размывание гель-хроматограммы:
-
У 2
F(V ) = J W ( У ) G(V , У )d У , (7)
-
У 1
где F ( V ) — гель-хроматограмма, W ( у ) — скорректированная на хроматографическое размывание гель-хроматограмма, G ( V , У ) — хроматограмма полимергомолога (функция размывания гель-хроматограммы), у 1 , у 2 — объемы удерживания, ограничивающие гель-хроматограмму образца.
Функция G ( V , у ) может представлять простую двухпараметрическую Гауссову функцию, а может быть, если добиваться наиболее точной коррекции хроматограммы, выражена четырехпараметрической асимметричной функцией. Выбор этой функции диктуется двумя обстоятельствами:
-
■ необходимостью получения точных результатов ( W ( у )) и
-
■ сложностью процедуры коррекции, представляющей при решении интегрального уравнения Фредгольма 1-го рода (к классу которых относится уравнение (7)) некорректную задачу. Подходы к этому выбору описаны в [1]. Процедуру коррекции хроматограммы той или иной сложности включают все ЭВМ-программы интерпретации гель-хроматограмм.
Далее, имея скорректированную хроматограмму W ( у ), необходимо получить калибровочную зависимость
V r = V r ( M ). (8)
Наиболее эффективна для точности интерпретации линейная зависимость (3), если ее получить для колонки, заполненной сорбентом, с линейной зависимостью VR от М, используя значительное число полимерных стандартов. Погрешность подобной калибровки уменьшается пропорционально корню квадратному из числа стандартов. Поэтому наиболее эффективно для калибровки линейной ГПХ-колонки использовать бимодальные полистирольные (ПС) стандарты, созданные в ИВС РАН [6], и ГПХ-колонки с линейной калибровочной зависимостью, процедура получения которой также разработана в ИВС РАН [6].
Калибровочные колонки V R = V R ( M ) — это основная проблема ГПХ. Ее просто решать, если обладать охарактеризованными по М узкодисперсными стандартами (фракциями) анализируемого полимера. Известны методы калибровки с использованием широкодисперсных фракций полимера с известным ММР. Существуют также методы калибровки на основе универсальной калибровочной зависимости Бенуа (1) и полимерных фракций с известными средними М ( Мw , Мn ) или характеристической вязкостью [ ^ ] [1]. Выражения для средних масс ( М w , М n ) приводятся далее.
Создание высокочувствительных детекторов для ГПХ на основе фотометров (нефелометров)
рассеянного света решило проблему калибровки для гомополимеров, превратив ГПХ в абсолютный метод определения их ММР.
В семидесятых годах на рынке появился малоугловой лазерный детектор светорассеяния LALLS. Созданный в восьмидесятых годах многоугловой лазерный детектор светорассеяния MALLS представляет наиболее эффективный детектор для ГПХ на сегодняшний день. Этот детектор вместе с концентрационным детектором (рефрактометром) позволяет определять не только М полимера, но и распределение по размерам макромолекул. А сравнивая размер макромолекулы, характерный для линейного полимера определенной молекулярной массы и того же химического состава, с измеренным в ГПХ-эксперименте, можно определить индекс разветвленности дм =
2 1/2
-
< rg > br [< ■ >^2)
M
Методы определения ММ и ММР
Метод
Преимущества, возможности
Недостатки
Классическое светорассеяние
Определение: М, < r g > 1/2 , А 2
Нет деструкции высокомолярных полимеров
Не дает информации по ММР, распределению < i g > 1/2. Ограничены возможности определения разветвленности, т.к. определяет М и < r g > 1/2 только для узкодисперсных полимеров. Результаты искажаются присутствием пыли, высокомолярных агрегатов
Классическая ГПХ
Недорогой метод, позволяет получить точное ММР лин. полимеров, для которых имеются стандарты и константы Марка—Куна. Можно получить при-ближ. ММР по ПС-стандартам
Неэффективна при нечетком механизме ГПХ и разветвленных полимерах
GPC + LALLS
ММР без стандартов. Распредел. по [ ^ ] из хроматограммы с универс. калибровкой и ММР полимера. Необязателен механизм ГПХ
Не дает информацию по распределению < r g > 1/2 из-за от
сутствия информации по I ( в )
ГПХ + вискозиметр
Измеряет распределение по [ ^ ]. При универс. калибровке определяет ММР.
Чувствительна к нарушению механизма ГПХ
GPC+MALDI TOF MS
То же, что метод 3, дает сведения о структуре молекул
Не дает информации по распределению < r g > 1/2
-
3. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РАССЕЯНИЯ СВЕТА ПОЛИМЕРНЫМИ РАСТВОРАМИ
где < r g > 1/2 — среднеквадратический размер макромолекулы (расстояние между ее концами), или радиус инерции, индексы br и lin относятся к разветвленной и линейной макромолекулам одного М . Поскольку размер более плотной разветвленной макромолекулы всегда меньше размера линейной макромолекулы соответствующей ММ, индекс разветвленности gМ меньше единицы.
В таблице приводится сравнение ГПХ— MALLS с другими методами определения М и ММР полимеров. Здесь не рассматриваются методы седиментации — диффузии [7] и лазерной корреляционной спектроскопии [8] — как дорогостоящие и недостаточно информативные для низкомолекулярной фракции полимеров.
Фундаментальная теория рассеяния света растворами полимеров изложена в работах Дебая и Зимма [9–11] и обобщена в руководстве [12]. Теоретические обоснования и приборное решение MALLS вместе с некоторыми полученными результатами изложены в обзоре Вьятта (Wyatt) [2].
Доступная информация о светорассеянии полимерными растворами изложена в монографии Кратохвила [13]. Математическое моделирование ГПХ с детекторами светорассеяния и вискозимет-рическим детектором изложено в работе Яу и Джексона [14]. Анализ точности определения ММР с помощью ГПХ с "on-line" детектором светорассеяния сделан в работах Прохазки и Кратох-вила [15, 16].
Интенсивность рассеяния света из единицы объема разбавленного полимерного раствора под углом О определяется уравнением:
R ! = MP ( О ) - 2 A2CM2 P 2( О ) + , (10)
Kc где Ro — избыток Релеевского отношения, P(θ) — функция рассеяния частицами, С — концентрация полимерного раствора (г/мл), М — молекулярная масса (вместо М можно использовать средневесовую молекулярную массу Мw в случае полидисперсных образцов), А2 — второй вириаль-ный коэффициент (мл∙моль/г), Кc — константа, которая для вертикально поляризованного света имеет вид
K с = —^- • (d n /d c )2.
A) N A
Здесь A 0 — длина волны падающего луча в вакууме, n 0 — показатель преломления растворителя при данной длине волны, N A — число Авогадро, d n /d c — инкремент показателя преломления полимера (может быть найден в литературе [17] или измерен непосредственно в эксперименте).
Избыток Релеевского отношения (сравнительно с растворителем) определяется следующим уравнением:
R o
( I o I o , solvent ) р
I 0 V
= f •
I o I o , solvent
I
где 1 О — интенсивность света (количество энергии, проходящей за единицу времени) в направлении под углом О к падающему лучу, 1 0 — интенсивность падающего (первичного) луча, 1 О solvent — интенсивность рассеяния света растворителем, V — объем рассеивающего раствора, ρ — коэффициент рассеяния между рассеивающим объемом и детектором, f — калибровочная константа, связанная с геометрией инструмента. Размерность R o — [L - 1] (см - 1 ).
Второй вириальный коэффициент А 2 определяет термодинамическое качество растворителя для данного полимера, связанное с его растворимостью. Высокое положительное значение А 2 характеризует термодинамически хороший растворитель. Для большинства полимерных систем А 2 уменьшается с увеличением М :
А 2 = М -О , (11)
где О е [ 0.15, 0.35 ] . Уравнение (11) иллюстрирует ухудшение растворимости с ростом М полимера.
Значение А 2 можно найти в литературе [17], или оно может быть измерено экспериментально DAWN-фотометром, используя стандартную диаграмму Зимма (см. дальше).
Функция рассеяния частицами (фактор рассеяния частицами) Р( О ) описывает угловую зависимость интенсивности рассеяния света
P О ) = R ,
R 0
где R и R 0 — соответственно избыток Релеевского отношения под углами О и 0 ° . Для малых молекул (у которых максимальное расстояние между двумя точками частицы не превышает A /20) угловая зависимость рассеяния света пренебрежимо мала и Р( О )= 1 для всех углов рассеяния. Важное свойство Р( О ) — его зависимость от размера частиц:
, 16 п . / 6 А 2
Р ( 6 ) = 1--- Sin I — I < r > + ... ,
3л2 I 2 J g
а для 6 ^ 0
мость R6 IKc (или Kc IR6) от sin2 (6 /2) и определены интерсепт при угле 0° m0 = d[R6 / Kc ]/d[sin2(6 /2)]
1 16 п . 2Г 6 ) 2
Р ^( 6 ) = 1 + —— Sin2| - I < r 2 > + , 3 Я2 V 2 J g
или
d [ Kc / R 6 ] /d[sin2( 6 /2)].
где X — длина волны падающего луча в данном растворителе ( X = X 0 /n 0), < r g > — средний квадрат
радиуса макромолекулы.
Квадратный корень из среднего квадрата радиуса — радиус инерции < r g > 1/2 — описывает
При угле 0° P ( 6 ) приближается к 1, М и < r g > 1/2 могут быть получены из уравнения (10) или (12). Например, решив уравнение (12) для М, получим
M=
размер макромолекулы в растворе независимо от ее формы. Если разделить частицу на N независимых элементов равной массы (например, сегментов макромолекулы), то
а если А 2 =0, то
r g
N
- Yr2
( N Z '
1/2
J
где ri 2 — квадрат расстояния i -го элемента от центра тяжести макромолекулы.
У гибкоцепного полимера каждая конформация имеет различные rg , и отсюда только средняя ве-
личина rg имеет практическое значение:
< rg 2 > 1/ 2
N
-Z< r2 t N Z
1/2
>
J
где < ri 2 > — среднее квадрата расстояния
i -го элемента от центра тяжести всех конформаций
2 1/2
и < rg 2 > 1/ 2 — среднеквадратический радиус
(в нм). Отметим, что среднеквадратический ради-
ус не идентичен геометрическому радиусу.
Уравнение (10) можно записать в обращенной форме, которая приблизительно линейна относительно s in2 ( 6 /2 )
K c
R 6
MP ( 6 )
+ 2 A 2 C + ....
Эксперименты выполняются обычно при низких концентрациях, и членами с высшими степенями концентраций можно пренебречь.
Уравнение (10) — основа расчета в программе "ASTRA" (WYATT-программа для использования в DAWN-фотометре), но расчеты по уравнению (12) можно также выполнить, используя специальный модуль "ASTRA".
Чтобы определить М и < r g > 1/2, должна быть измерена концентрация образца (с помощью концентрационного детектора), построена зависи-
Г KT
V R6
M=
Л-1
2 A2C
J
Г K c
Л-1
R
V 6 J
,
,
и для размера (радиуса инерции) молекулы
< rg >"2=^X° 7m0M.
4 n n 0
Если определены С , , М , и < r g > * /2 для каждого фрагмента хроматограммы, то можно определить их средние величины.
Среднечисленную М :
M n
Z C, Z C , / M, '
Средневесовую М :
z -Среднюю М :
M w
M z
= Z CM, = Z C,
= X CM?
Z CM, ■
Среднечисленный среднеквадратичный радиус:
z < r g >, C,/ Mt r g n = Z C , / M ,
.
Средневесовой среднеквадратичный радиус:
2> _ z< rg >, c, < rg >w = z c,
.
z -Средний среднеквадратичный радиус:
2 _ ^< rg >.CM g z = ^m. "
Поскольку хроматограмма в ГПХ представляет суперпозицию хроматографических зон полимергомологов, каждый фрагмент хроматограммы содержит смесь полимергомологов. Вследствие этого Mt и < r g > , в вышеуказанных уравнениях представляют соответственно средневесовые и z -средние величины. Следовательно, ГПХ с детектором светорассеяния имеет тенденцию завышать среднечисленные величины М и < r g > 1/2. Однако, используя высокоэффективные колонки для ГПХ, можно получать в каждом фрагменте хроматограммы очень узкие фракции полимергомологов и определять таким образом точные значения указанных средних величин.
Концентрация полимеров в каждом фрагменте хроматограммы определяется рефрактометрическим детектором. Для этого предлагаются три метода:
-
1. Массовый метод. Концентрация рассчитывается из массы пробы, отношения сиг-нал/показатель преломления R1-детектора (единиц рефракции на один вольт) и объема фрагмента хроматограммы. Метод позволяет рассчитать инкремент показателя преломления d n /d c , необходимый для расчета М .
-
2. d n/ d c-метод не требует изменения массы пробы, но требует знания постоянной детектора (U/R1-индекс).
-
3. Комбинированный метод использует массовый метод для расчета концентраций каждого фрагмента хроматограммы и d n /d c -метод для расчета М . Преимущество метода 3 — в отсутствии необходимости знать постоянную R1 детектора.
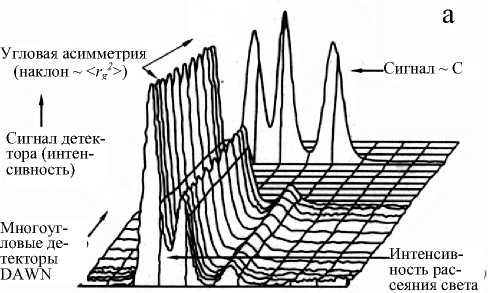
(~ M w )
Объем удержания
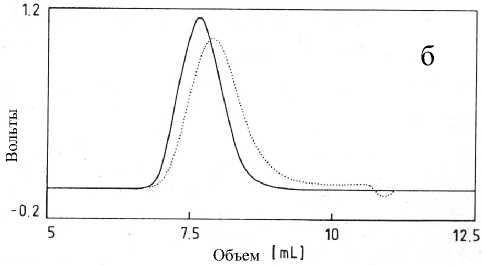
Рис. 1. Гель-хроматограммы полистирольного стандарта PS NBS 706. а — смещение R1 и MALLS-гельхроматограммы; б — R1 (точечная линия) и MALLS (сплошная линия)
зволяет определить М, < r g > 1/2 и фрагменты хроматограммы объемом 0.01 мл.
Эти результаты позволяют получить средние величины < М> и < r g > 1/2 полимеров.
На полученные результаты влияет величина второго вириального коэффициента А 2. Это влияние, направленное в сторону завышения результатов, увеличивается с ростом М полимера (до 10 % для М =3∙106 Да). Последнее связано с зависимостью А 2 от М (11).
Зависимость М от объема удерживания различается у разных полимеров вследствие трех обстоятельств:
-
■ различной молекулярной массы сегментов макромолекулы;
-
■ различий в степени набухания макромолекулярного клубка;
-
■ различий в его плотности вследствие разветвленности макромолекулярной цепочки.
Как указано выше, интенсивность рассеянного света определяется двумя уравнениями: (10) и (12). Уравнение (12) имеет преимущество линейности в более широком диапазоне М. При использовании же уравнения (10) необходимо при М больше 5∙105 Да применять полиномиальное выражение высшего порядка.
Определение размера макромолекулы
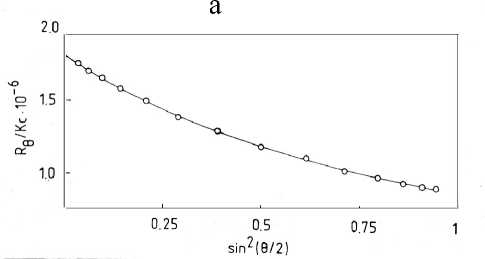
Размер макромолекулы — важная физическая характеристика, доступная для определения в GPC—MALLS эксперименте. Как указывалось выше, его можно определить из наклона зависи мости Re IKc от sin2 (e /2) или Kc IRe от sin2 (e 12) (рис. 2). Точность определения сильно зависит от соотношения сигнал/шум. Поэтому точно определяется только < rg > средней части
ММР. Можно сравнить полученные таким образом результаты с результатами из уравнений Флори—Фокса [7]
< r 2 >1,2 = * Г [ П М Г g
и Птицына—Эйзнера [7]
Ф = 2.86 - 1021 - ( 1 - 2.63 е + 2.86 е 2 ) , (14)
где £ = (2 a - 1) 13, а — экспонента уравнения
б
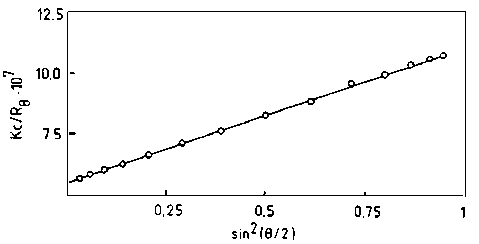
Рис. 2. Зависимость R θ /K C от sin2( θ/2 ) (a) и K C /R θ от sin2( θ/2 ) (б) для гель-хроматограммы полистирольного стандарта М= 1 840 000
Марка—Куна (2). Здесь К п и а — константы для данного полимера, растворителя и температуры. Обозначая [ п ] в дл/г (1 дл/г=100 см3/г), получаем < r g > 1/2 в сантиметрах. Расхождения величин < r g > 1/2 ’ полученных методом MALLS и из [ п ] по процедуре (13)–(14), не превышают 10 %. Нижний лимит определения < r g > 1/2 методом MALLS = 10 нм.
Двойная экстраполяция результатов светорассеяния по e и С показана на рис. 3, при малых концентрациях полимера можно ограничиться экстраполяцией только по e (рис. 2).
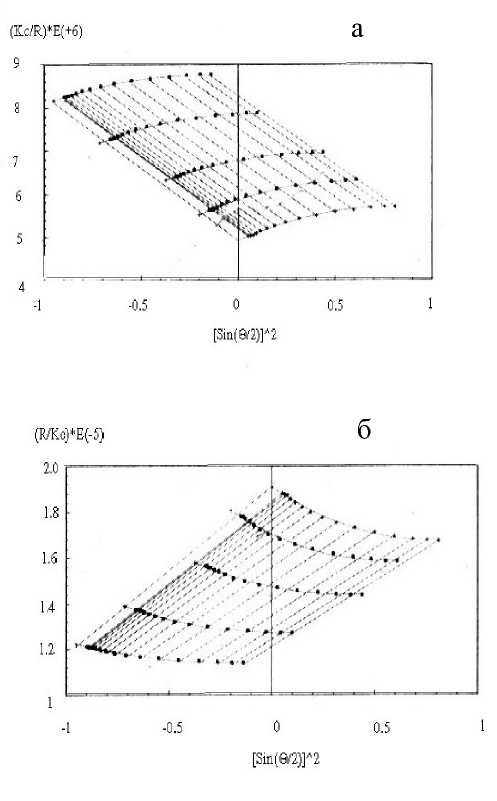
Рис. 3. Диаграммы двойной экстраполяции (по С и e ) Зимма (а) и Дебая—Берри (б), автоматически полученные с помощью программы "AVRORA" из пакета программ "DAWN"
Рис. 4 представляет логарифмические зависимости < r g > 1/2 от М . Для линейных полимеров (рис. 4, а) этот наклон равен 0.5–0.6. Для разветвленных (рис. 4, б) = 0.38. Если < r g > 1/2 представить как зависимость от V R , можно определить средние величины < r g > 1/2. Для широкодисперсного полистирольного стандарта PS NBS 706 эти величины составляют соответственно:
-
< r g > П /2 = 12нм,
-
< r g > W /2 = 23нм,
-
< r 2 >У 2 = 29нм.
gz
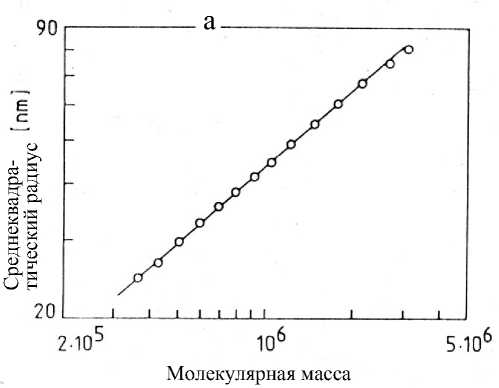
Радиус-метод
б
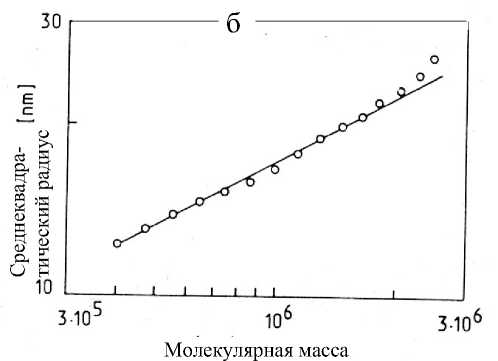
Рис. 4. Среднеквадратический размер макромолекулы как функции от М для ПММА (наклон 0.57) (а) и алкидной смолы (наклон 0.38) (б)
Характеристика разветвленности
При сопоставлении < r g > 1/2 линейных (lin) и разветвленных (br) макромолекул одной М и идентичного химического состава можно определить фактор разветвленности (9). g M можно определить как функцию М . Поскольку разветвленные макромолекулы более компактны, чем линейные, g M всегда меньше 1.
а
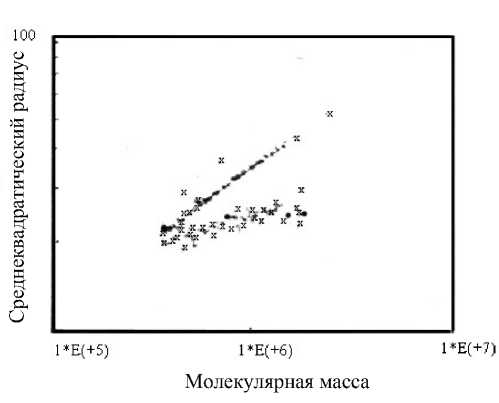
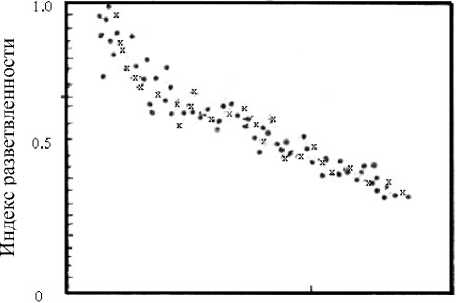
3»Е(+5) 1*Е(+6) 2*Е(+6)
Молекулярная масса
Рис. 5. Молекулярно-массовая (ММ) зависимость индекса разветвленности для линейного (х) и разветвленного ( • ) ПММА. а — ММ-зависимость < r g > 1 2 ; б — ММ-зависимость gM разветвленного ПММА. Программа "EASI" пакета программ "DAWN" позволяет рассчитать g М , а также B w — средневесовое число ветвлений в макромолекуле и среднюю длину ветвей при предположении типа ветвления
Наклон зависимости в < r g > 1/2 от М позволяет определить конформацию макромолекулы: при наклоне 0.5–0.6 — молекула разветвленная, при меньшем 0.5 (у сферы 0.33) — молекула клубкообразная, при наклоне, близком к 1, — палочковидная. Поскольку в ГПХ, особенно воднорастворимых полимеров, могут быть нарушения механизма хроматографии с наложением адсорбции при высокой М , лучше сопоставлять z -средний размер < r g > , /2 со средневесовой М — Mw . Рис. 5 показывает зависимость g M от М полимера.
Другая возможность идентификации разветвленных макромолекул — это использование двойной логарифмической зависимости [ п ] от М . Из универсальной калибровки Бенуа (1) и измерений М с помощью MALLS или LALLS можно определить [ п ] как функцию М и вычислить средние величины [ п ]. Это определение идентично определению с помощью ГПХ с вискозиметрическим детектором. Используя универсальную калибровочную зависимость, можно определить при этом и М .
На рис. 6 показана зависимость [ п ] от М для линейного ПММА (наклон 0.72). Рис. 7 показывает соответствующую зависимость для двух образцов феноксиполимера. Отклонение от линейности свидетельствует о наличии разветвленных молекул в этих образцах.
Рис. 8 показывает R1-хроматограммы и зависимость М ( V R ) для двух образцов поли-(3-0-метакрилоил) глюкуроновой кислоты. Смещение зависимостей указывает на разветвленность образца ( • ). Хроматограмма ( о ) смещена к низшим объемам элюции. В результате, при обычной ГПХ образец ( • ) был бы определен как более низкомолекулярный.
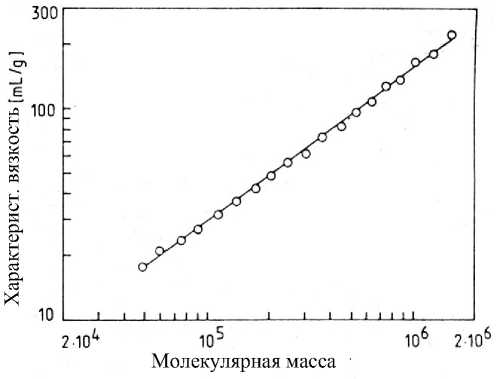
Рис. 6. Зависимость [ п ] от М ПММА
Если имеется линейный стандарт полимера той же химической структуры и М , то параметр разветвленности может быть определен с использованием уравнения (11):
дм =
M in
Мк ^ Vi br
х ( a + 1)/ e
) Vr
где М lin и М br — молекулярные массы линейного и разветвленного полимеров, V R — указывает на идентичный объем удерживания, а — экспонента
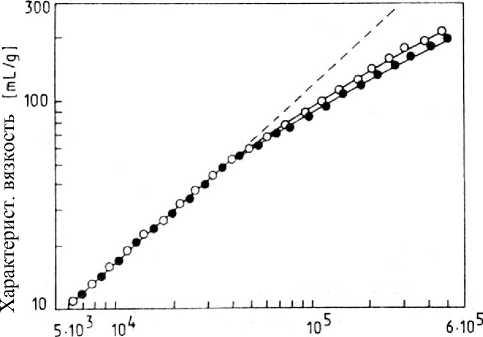
Рис. 7. Зависимость [ п ] от М для феноксисмол UCAR РКНС ( о ) и UCAR PKHJ ( • )
Молекулярная масса
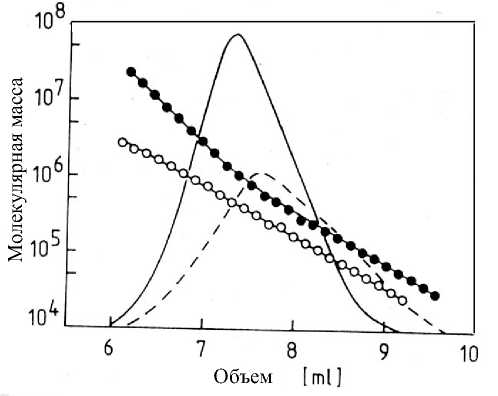
Рис. 8. М как функция UR для двух образцов по-ли-(3-0-метакрилоил) глюкуроновой кислоты, совмещенная с R1— ГПХ-хроматограммой уравнения Марка—Куна (2) для линейного полимера, е — параметр протекания макромолекулы: ее [0.5, 1.5].
Рис. 9, а показывает интересный пример применения ГПХ с MALLS (90 ° ) и R1-детекторами для этилового эфира поли-(-2-(D)-глюкопирано-зил-3-оксиметил) акриловой кислоты. С помощью MALLS-детектора получается бимодальная хроматограмма, а R1-детектора — унимодальная. Второй пик на MALLS-хроматограмме объясняется присутствием сильноразветвленных макромолекул или агрегатов в малых концентрациях, незаметных для R1-детектора (но детектируемых с высокой чувствительностью при использовании MALLS). Аналогичный пример — R1 и MALLS совмещенные программы смеси белков (рис. 9, б).
ЗАКЛЮЧЕНИЕ
Комбинация ГПХ с MALLS-детектором обеспечивает:
— Определение ММР и получение средних М для калибровки колонок.
— Определение распределения макромолекул по размерам и моментов этого распределения.
— При универсальной калибровке колонок определение распределения по [ п ] и коэффициентов Марка—Куна.
— Характеристику разветвленности макромолекул, используя зависимость < r g > 1/2 от М , [ п ] от М и М от V R , определение параметра разветвленности g M как функции М .
— Высокочувствительное детектирование минорных высокомолекулярных фракций и агрегатов полимера.
— Исследование приборного уширения и деструкции полимеров при ГПХ.
— Получение полезной информации для интерпретации результатов обычной ГПХ (определения ММР и разделения по < r g > 1/2 для реперных образцов исследуемых полимеров).
Другие варианты определения разветвленности макромолекул показаны в таблице.
Список литературы Определение молекулярной массы, размера и разветвленности макромолекул с помощью двухдетекторной ГПХ. Использование ГПХ с рефрактометрическим детектором и многоугловым лазерным нефелометром (Malls)
- Belenkii B.G., Vilenchik L.Z. Modern Chromatography of Macromolecules. Elsevier, Amsterdam, 1983. 450 p.
- Wyatt P.J.//Anal. Chim. Acta. 1993. V. 272, N. 1. P. 1-40.
- Chakel L.//International Laboratory. 1994, Nov.-Decemb. V. 24, N. 6. P. 21-28.
- Gankina E.S., Belenkii B.G.//Handbook of Thin-Layer Chromatography/Еd. J. Sherma and B. Fried. Marcel Dekker Inc., 1991. 1047 p.
- Belenkii B.G.//Pure & Appl. Chem. 1979. V. 51, N. 7. P. 1519-1535.
- Alexandrov M.L., Belenkii B.G., Gotlib V.A. and Kever E.//J. Microcol. Sep. 1992. N. 4. P. 385-392.
- Цветков В.Н., Эскин В.Э., Френкель С.Я. Структура макромолекул в растворах. М.: Наука, 1964. 719 c.
- Виленчик Л.З., Беленький Б.Г., Нестеров В.В. и др.//ДАН СССР. 1987. Т. 295. С. 119-121.
- Debye P.//J. Appl. Phys. 1944. V. 15. P. 338-342.
- Zimm B.H.//J. Chem. Phys. 1945. V. 13, N. 4. P. 141-145.
- Zimm B.H.//J. Chem. Phys.. 1948. V. 16. P. 1093-1099.
- Эскин В.Э. Рассеяние света растворами полимеров и свойства макромолекул. Л.: Наука, 1986. 288 c.
- Kratochvil P. Classical Light Sсattering from Polymer Solutions//Polymer Science Library/A.D. Jenkins (ed). Elsevier, Amsterdam, 1987.
- Jackson C. and Yau W.W.//J. of Chromatogr. A. 1993. V. 645, N. 2. P. 209-217.
- Prochazka O. and Kratochvil P.//J. Appl. Polym. Sci. 1986. V. 31, N. 3. P. 919-928.
- Prochazka O. and Kratochvil P.//J. Appl. Polym. Sci. 1987. V. 34, N. 6. P. 2325-2336.
- Polymer Handbook (3rd ed)/J. Brandrup and E.H. Immevgut (eds.). John Wiley & Sons, N.Y., 1989.
- Podzimek S.//J. Polymer Sc. 1994. V. 54, N. 1. P. 91-103.
- Wayatt Technology Corp. Application Notes.


