Асимметричный конденсатор, закон Кулона и ртутные движители

В статье сделана попытка дать объяснение силы, возникающей в асимметричном конденсаторе, известной как «эффект Бифельда-Брауна» или эффект «лифтера», как вызванной электростатическим кулоновским взаимодействием поверхности заряженного конденсатора с поверхностным зарядом Земли. Дан сравнительный анализ величинам силы, полученной в марте 2003 года Исследовательской Лабораторией армии США, Адельфи, Мэриленд 20783-1197 «Сила на Асимметричном конденсаторе» и расчетной. Также дана оценка подъемным силам в приведенных вариантах. Приведены материалы из заявок на изобретения, предлагающие решения по использованию указанного эффекта без применения высокого напряжения.

До настоящего времени академическая научная литература старательно обходит существование «Эффекта Бифельда-Брауна», открытого еще в 1921 году. Вариантом его особо яркого проявления считается возникновение подъемной силы в различных конструкциях асимметричного конденсатора, имеющего значительные конструктивные отличия электрических обкладок, получившее название эффект «лифтера». И хотя количество различных конструкций, использующих эффект, в том числе запатентованных, приведенных на видеороликах, размещенных в Интернете, исчисляется десятками, попытки какого-либо его объяснения сделаны только в Википедии или частными лицами. При строгом их рассмотрении приведенные объяснения не стыкуются с общепринятыми аксиомами физики. Ни одна мировая академическая школа пока не дала существующему эффекту научного обоснования, подтвержденного соответствующими экспериментальными данными. И это дает автору право изложить собственный взгляд на его объяснение, тем более что представленное теоретическое обоснование строится строго в рамках существующих научных парадигм.

Автор будет благодарен всем, кто найдет логические нестыковки или ошибки в сделанных им теоретических выводах.

За последние десятилетия самое серьезное исследование упоминавшихся эффектов было представлено в опубликованном в Интернете отчете от марта 2003 года Исследовательской Лаборатории армии США, Адельфи, Мэриленд 20783-1197 «Сила на Асимметричном конденсаторе» [1]. Примечательно, что экспериментаторы начали с того, что решили убедиться, что эффект в самом деле реально имеет место. С.Фази (АРЛ) и т. Bahder (АРЛ) изготовили три варианта простых асимметричных конденсаторов, аналогичных вариантам, представленным в Интернете. Во всех трех случаях они убедились, что на конденсаторах действительно возникает сила при подаче на электроды высокого напряжения. Все три конструкции, с которыми проводили опыты, имели различную геометрию, но у всех была одна одинаковая конструктивная особенность, заключающаяся в том, что один электрод был тонким, и другой очень широким (асимметричные размеры).

К сожалению автора, в опубликованном отчете недостаточно четко изложено взаимное расположение тонкого и широкого электрода, их заряда, расположения относительно поверхности Земли и направления возникающей силы. Так же, судя по фотографиям, эксперименты проводились в замкнутом помещении, размеры которого вполне сопоставимы с размерами испытуемых конструкций. Из-за этого между ниже приведенным теоретическим обоснованием некоторых эффектов и выводами экспериментаторов либо имеются противоречия, не объясненные автором, либо выводы отчета не учитываю всех нюансов эксперимента. Во всяком случае, показанная в отчете картина не дает возможности автору их полностью правильно оценить.

Далее в отчете сделана попытка получить теоретическое обоснование полученной величины подъемной силы. Первоначально была рассмотрена теория «ионного ветра», принятая на настоящий момент в качестве истинной для объяснения «Эффекта Бифельда-Брауна» в свободной энциклопедии – Википедии [2].

Экспериментально было установлено, что фактическая сила, возникающая на асимметричном конденсаторе, значительно больше, чем теоретически возможная от «ионного ветра». Тем самым такое ныне принятое объяснение получается совершенно несостоятельным. Осталось только исправить Википедию. В то же время, порядок полученной силы соответствует теоретической расчетной величине, если рассматривать асимметричный конденсатор как электрический диполь значительных размеров, взаимодействующий с неравномерным электрическим полем, полученным за счет ионизации воздуха под воздействием электрического поля самого диполя. Но такое объяснение не встраивается в существующие парадигмы физики и требует введение в теорию электрического поля неких дополнительных параметров, теоретически не доказанных и экспериментально никак не подтвержденных. Тем более было установлено, что и в четвертом варианте с подвесным проводом, являющимся одиночной «бесконечной» обкладкой конденсатора, также наблюдается подъемная сила (см. рис. 1).

Рис. 1. Одиночный провод под высоким напряжением

А в этом варианте объяснять эффект возникновением «ионного ветра» или «ионного дрейфа» вообще неприемлемо, так как вторая обкладка фактически отсутствует. Или необходимо учитывать влияние стен и потолка, расположенных достаточно далеко. То есть, полученные результаты опытов противоречат попыткам теоретически их объяснить.

Тупиковая ситуация, из которой автор предлагает свой выход.

Так как любой конденсатор в рабочем состоянии – это система из двух различных обкладок с зазором между ними, представляющая собой накопленный заряд:

Q = c x U где

Q – заряд конденсатора;

с – емкость конденсатора;

U – напряжение на конденсаторе.

Таким образом,   отрицательно заряженная   обкладка конденсатора   является   элементом, который необходимо рассматривать  с точки зрения поверхностных  состояний безотносительно положительно заряженной обкладки.

Согласно теории таммовских поверхностных  состояний электронов, «…в случае металлов (в отличие от полупроводников и диэлектриков) поле поверхностного заряда проникает в глубину кристалла лишь на расстояние, меньше чем постоянная решётки: оно очень интенсивно экранируется положительным зарядом, возникающим в тонком приповерхностном слое металла вследствие частичного ухода из этого слоя электронов проводимости. Таким образом, заполнение нижайших поверхностных уровней электронами (а именно это и происходит при зарядке конденсатора на отрицательно заряженной обкладке!) приводит к образованию на поверхности металла дополнительного электрического двойного слоя…. Особенно велика роль поверхностных состояний электронов в связи с тем, что попавшие в них электроны способны создавать очень большой отрицательный поверхностный заряд» [3]. То есть, на отрицательной обкладке конденсатора появляются «поверхностные состояния электронов», или поверхностный заряд Qпов,    который в соответствии с законом Кулона обязан взаимодействовать с поверхностным зарядом Земли. На положительной же обкладке конденсатора наоборот сохраняется запрещенная зона, которая, возможно, видоизменяется. Но тогда поверхность положительной обкладки конденсатора с точки зрения рассматриваемого воздействия ничем не отличается от поверхности просто металла, у которого существует запрещенная зона и электроны которого находится в потенциальной «яме» [4]. Поэтому кулоновские силы никак себя не проявляют, так как для рассматриваемого воздействия отличия нет, хотя и вероятно, что имеется какое-то иное измененное ее взаимодействие с внешним электрическим полем из-за возможного искажения электронного поверхностного слоя из-за приложенного положительного заряда.

Рассмотрим это взаимодействие отрицательной обкладки конденсатора с поверхностным зарядом Земли.

Построим, с учетом сопоставления геометрических размеров, схематическую теоретическую модель взаимодействия. Для характеристики уровня зарядов на рассматриваемой модели

Доклады независимых авторов 2018 выпуск 42 воспользуемся таким физическим параметром, как поверхностная плотность заряда.

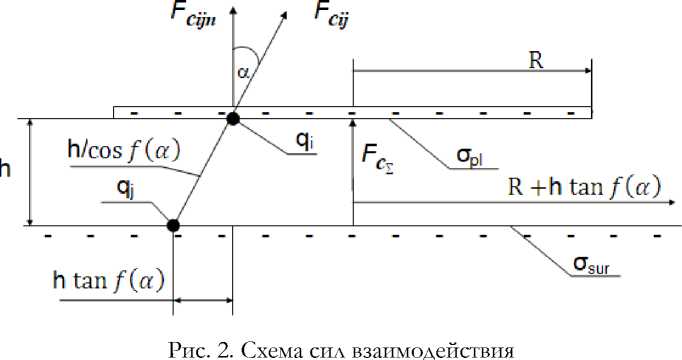
Итак, рассмотрим схему сил взаимодействия (см. рис. 2)

Имеется бесконечная плоскость с отрицательным

Кл распределенным зарядом osur м . Над ней находится плоский с

Кл конечными размерами отрицательный распределенный заряд opl м в виде круга радиусом R и площадью Spl , расположенный на произвольной, имеющей возможность изменяться, высоте h над бесконечной плоскостью.

Пусть плоский заряд над поверхностью образован совокупностью точечных зарядов q_i, а сама плоскость – совокупностью точечных зарядов qj_. Данное допущение вполне правомочно, так как, в итоге, любой отрицательный заряд образован электронами, которые, в свою очередь, являются минимальными отрицательными точечными зарядами.

Рассмотрим в ней действие кулоновских сил. Пусть взаимодействие каждого точечного заряда q_i на плоском заряде происходит с каждым точечным зарядам qj , расположенным на радиусе h tan /(а) от нормали. В этом случае сила Fc_i j между двумя такими точечными зарядами, согласно закону Кулона [5], будет определяться по следующей формуле:

Fc_ij = к х

4 i х Я )

А2/

' [cos /(а)]2

где ^a — переменный от 0 до 90^о угол между произвольной силой Fci j , расположенной на радиусе h ^tan Дк) на отрицательно заряженной плоскости, и нормалью к рассматриваемому точечному заряду q_i на конечном заряде. Тогда проекция на нормаль силы Fc_i j , действующей на одиночный точечный заряд q_i , от зарядов qj_. расположенных на радиусе h ^tan ДД будет определяться по следующей формуле:

^Fctjn = Fc ^{х cos /(a)}

Горизонтальные составляющие, расположенные по радиусу, взаимно уничтожаются и не оказывают на заряд qi никакого воздействия. В результате суммарная кулоновская сила в пределах угла a, действующая на конечный заряд, вверх, определяется по формуле:

^f l X ^f = 1^,

направленная по нормали х cos /(a)

или

Fc2

= Vk х 2 ' х qj х cos /(a)

2  hT/

/ [cos /(a)]2

или

Fc ^ = k х ^ ^2 ^ ^j х [cos/(a)]³

Так как количество всех зарядов qi,   участвующих во взаимодействии равно

2^ = °pi х nR2 = °pi х s pi = const то формула примет вид:

^Fc^ = ^k ° pi^s_Pi ^х 2 ^ 2 ^{х [cos /(a)] 3}

Так как количество всех зарядов qj_, участвующих в рассматриваемом взаимодействии равно

^^j = Csur х S/(a)sur = Csur х n[R + htan /(a)]2

то итоговая формула примет следующий вид:

Fc2=knspi°pi°sUrх 2[R+hthn /(a)] х [cos/(a)]3

или

Fc2

^knFpi^api ° sur

х ^ [ h + tan /(a) ] ² х [cos /(a)]³

или, во всем диапазоне угла ^a от 0 до 90^о:

a

.

^Fc Z

^ ⁿ ^ pl ® pl ® sur ^x

90°

JI ?

+ tan /(a)]2 x [cos (a)]3d(a)

В полученной формуле обращает на себя внимание параметр Если эксперименты с асимметричном конденсатором проводились в закрытом помещении, то это приводило к искажению влияния электрического поля Земли, и, соответственно, к искажению правильности трактовки полученных результатов.

Рассмотрим вариант, когда h много больше R. Так как в этом случае влияние от имеющего возможность изменяться, параметра R/h стремится к нулю, формула кулоновской силы воздействия на конечный распределенный отрицательный заряд, расположенный над бесконечной отрицательно заряженной плоскостью, примет следующий вид:

90 ^°

J [tan (a)]²

x [cos (a)]3d(a)

Fcy = knSpiCpiCsur x или

^Fc z

^knS pl ^ pl ^ sur ^X

90 ^°

J [sin (a)]2

x cos (a)d(a)

или

Fc^

= ^knSpl O pl O_S ur ^X

90 ^°

J{1 - [cos (a)]2}

x cos (a)d(a)

или

' 90°

^Fc^ = ^knSpl C pl C_sur ^x J cos

90 ^°

(a)d(a) - J [cos (a)]3d(a) 0

или

90 ^°             90 ^°                        90 ^°

^Fc Z

= knSplOplOsurl J sin (a) - {3 J [cos (a)]2sin (a) + 3 J cos (a)d(a) 11

или

Fc^ = knSplGplGsur x [1 - 3 J sin (a)]

или

^Fc x = 3 ^knSpl^Cpl^Csur

Так как коэффициент пропорциональности

k 4П£0

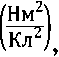
То итоговая формула примет вид:

FcY = T2T0Spicpicsw где

Кл

Opl и Osur , ( м конечного

) – поверхностные плотности зарядов заряда и бесконечной плоскости соответственно;

S_pl , (м²) - площадь конечного заряда;

= 8,854 x 10 - ¹² ( Ф )

^E 0

- электрическая постоянная.

Следовательно, подъемная кулоновская сила, действующая на конечный заряд, для рассматриваемого варианта является величиной постоянной и не зависит от расстояния между бесконечной заряженной плоскостью и конечным распределенным зарядом.

Рассмотрим полученную формулу для условий Земли. «Средняя поверхностная плотность электрического заряда Земли dQ/dS= -1,15 10-13Кл/см2»[6].    Рассчитаем подъемную силу конечного распределенного заряда в 1 Кл/м2 и площадью 1 м2. Дано:

σ_sur = 1,15х 10^-13 Кл/см²= 1,15х10^-9 Кл/м²

σ_pl х S_pl = 1 Кл

Fcs =

12e0

Spl^pl ^sur

112 X 8,854X IO"12

x 1 x 1,15 x IO”9

----------X 1,15 X 103 = 10,8 H = 1,1 kF 12X8,854

Таким образом, за счет поверхностного заряда Земли, при поверхностной плотности конечного заряда в 1 Кл/м2 на площади 1 м2 создается подъемная сила, равная 1, 1 кГ/Кл.

Необходимо учитывать, что «…плотность таммовских (поверхностных) состояний (электронов) должна определяться плотностью поверхностных атомов, т. е. составлять 10¹⁴–10¹⁵ см^-2. Экспериментально это было подтверждено в 1962 г.» [7].

Вернемся к отчету Исследовательской Лаборатории армии США, Адельфи, Мэриленд 20783-1197 «Сила на Асимметричном конденсаторе» [1]. На испытуемых трех вариантах асимметричных конденсаторов в качестве отрицательной обкладки использовалась алюминиевая фольга размером 20х4 см. Оценим полученную на ней плотность таммовских поверхностных состояний электронов. Очевидно, что в фактически испытуемых конструкциях эти состояния будут неравномерны, и выявить это возможно только эмпирически путем фактических замеров. Поэтому, так как устраивает точность на уровне порядка величины, будем считать, что каждый атом поверхности алюминия создает 1, 2, 3 … и т. д. поверхностный электрон при приложении к конденсатору постоянного высокого напряжения. Алюминий имеет кубическая гранецентрированная параметры решётки 4,050 Å [8]. Следовательно, его поверхность образована

N =-----1 x------1—= 12,19 x 1018

4,05 x 10 "10 4,05 x 10 -10/ атомов на один кв. метр поверхности.

Если на один поверхностный атом алюминия находится 1 электрон в «поверхностном состоянии», то величина поверхностного отрицательного заряда 1 м2 будет:

e x N = 1,6x10 -19 x 12,19 x 1018 = 1,95 Кл где e =- 1,6 x 10 -19 Кл - величина заряда электрона.

Создаваемая подъемная сила 1 м2 отрицательной обкладки в этом случае составит:

Fcz = 1,1 x 1,95 = 2,145 кГ

А подъемная сила полоски алюминиевой фольги размером 20х4 см. будет:

2,145 х 0,2 х 0,04 = 0,017 кГ = 17 г.

Рис. 3 Одиночный рабочий элемент.

Так как в упомянутых экспериментах с асимметричными конденсаторами единичным рабочим элементом являлась конструкция, приведенная на рис. 3, то очевидно, равномерно распределенного наведенного высоким напряжением поверхностного состояния электронов в таком варианте существовать не может. То есть, подъемная сила алюминиевой полоски будет в несколько раз меньше. А тогда расчетная величина подъемной силы практически идеально состыковывается с полученными результатами, приведенными в отчете «Сила на асимметричном конденсаторе» [1].

Таким образом, теоретическое обоснование эффекту Бифельда-Брауна, данное на основании закона Кулона и теории таммовских поверхностных состояний электронов, гораздо более достоверно, чем имеющиеся.

Тогда рассмотрим, насколько возможно создание практических летательных аппаратов на базе сделанного объяснения. Обращают на себя два момента. Первый. Если увеличить на один поверхностный атом количество электронов, находящихся в таммовских поверхностных состояниях с единиц до десятков, можно получить вполне практически приемлемую величину подъемной силы. Второй. Сомнительно, что возможно получить необходимое по величине поверхностное состояние электронов на каком-либо металле на базе конденсатора. Этому препятствует пробой конденсатора, и, по мнению автора, это происходит, как только в поверхностное состояние «пытается перейти» второй электрон поверхностного атома металла. Причем, любого металла.

Следовательно, для практического применения необходимо создавать специальный металл, у которого таммовское поверхностное состояние электронов носит естественный характер, так как в соответствии с общепринятыми научными взглядами, все привычные нам металлы наоборот имеют на поверхности запрещенную зону, где не могут находиться электроны. И понятно, что необходимый нам должен иметь уникальные отличия в своих свойствах от известных..

Однако, есть один металл, чьи свойства в твердом состоянии недостаточно исследованы, так как это не имело особого практического смысла. Этот металл – ртуть, которая широко используется в жидком и парообразном состоянии. Имеется практически не используемая «…твердая ртуть – бесцветные кристаллы: до 79К существует ромбоэдрическая кристаллическая модификация α (при 78К α =0,29925нм, β= 70,74о…» [9]. При этом «…кусочки твердой ртути при соприкосновении друг с другом слипаются почти так же легко, как и жидкие ее капли» [10]. Другими словами, при соприкосновении двух тел из твердой ртути в обычных нормальных условиях (не в космосе!) между ними происходит холодная сварка. Все другие металлы при таких условиях могут соединиться только в процессе многолетней диффузии, да и то, только при значительном сжатии и деформации. Так что, это свойство ртути является уникальным среди металлов. Рассмотрим смысл «холодной сварки».

«Холодная сварка – сварка давлением при значительной пластической деформации без нагрева свариваемых частей внешними источниками тепла. Метод холодной сварки основан на использовании пластической деформации, с помощью которой разрушают на свариваемых поверхностях хрупкую пленку окислов - основное препятствие для соединения металлов. Образование цельнометаллического соединения происходит за счет возникновения металлических связей между соединяемыми металлами. Эти связи возникают между атомами при сближении поверхностей соединяемых металлов на расстоянии порядка (2,8)^10 - мм в результате образования общего электронного облака (!!!) , взаимодействующего с ионизированными атомами обеих металлических поверхностей» [11]. В случае если бы на поверхности твердой ртути существовала запрещенная зона для нахождения в ней электронов, никакого общего электронного облака при простом соприкосновении, в отсутствии деформации, в обычных условиях возникнуть не могло, и холодная сварка не могла бы осуществиться. Следовательно, вывод автора о наличии на поверхности твердой «замороженной» ртути электронов в таммовском поверхностном состоянии вполне обосновано. Рассчитаем его по аналогии с алюминиевой поверхностью.

Для этого определим поверхностную плотность атомов твердой ртути. Количество N атомов ртути на 1м2 поверхности составит:

ЛГ =---------------------------

2 х 0,29925 X 10“9 X sin

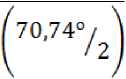
х------------------

0,29925 X 10"9Х cos

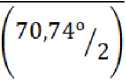
----------ХЮ18 0,3464 X 0,2440

= 11,83 X 1018'

атомов на один кв. метр поверхности (см. [9]).

В случае, если в «поверхностном состоянии» находится только 1 из 80, составляющих атом ртути, то величина поверхностного отрицательного заряда 1 м2 твердой ртути будет:

е х N = 1,6 х 10 "19 х 11,83 х 1018 = 1,893 Кл

где е =- 1,6 х 10 -19 Кл - величина заряда электрона.

А создаваемая подъемная сила 1 м2 твердой ртути в этом случае составит:

Fc^ = 1,1 x 1,893 = 2,082 кГ

Так как такое состояние является естественным состоянием, логично исходить из того, что таких электронов будет половина, то есть 40. И тогда

Fc^ = 1,1 x 1,893 x 40 = 83,3 кГ

Такая величина заряда для образования подъемной силы является вполне достаточной для практического создания летательных аппаратов, работающих за счет внешнего электрического поля.

На такой вариант подана заявка на изобретение RU 2016 117 049 А «Движитель Степанова».

Реферат.

Движитель предназначен для преобразования энергии электрического поля в перемещение тел или во вращение двигателя. Для этого используются явление, описанное эффектом Бифельда-Брауна. На движителе образована поверхность с распределенным отрицательным зарядом. В отличие от эффекта Бифельда-Брауна, такая поверхность получена без применения электрического напряжения. Для ее получения использована ртуть, приведенная в твердое состояние и в дальнейшем поддерживаемая при температуре ниже минус 38,8 оС. При этом ее поверхность представляет собой сплошной слой атомарных электронов. Она взаимодействует с отрицательно заряженной поверхностью земли в соответствии с законом Кулона, в результате чего возникает подъемная сила.

С технологической точки зрения сложно представить себе практическую конструкцию, несущие элементы которой выполнены из ртути. Все время имеется опасность перехода ее в жидкое состояние и разрушение возможного летательного аппарата. Выход из ситуации дан в заявке на изобретение RU 2016 146 063 А «Движитель».

Реферат.

«Движитель является вариантом исполнения движителя Степанова, в котором используется твердая «замороженная» ртуть, и предназначенного для преобразования энергии внешнего электрического поля в перемещение тел или во вращение двигателя. На движителе образована поверхность с распределенным отрицательным зарядом, полученная без применения электрического напряжения. Для ее получения использована ртуть, приводимая в твердое состояние и в дальнейшем поддерживаемая при температуре ниже минус 38,8 оС. Для улучшения технологичности при изготовлении и эксплуатации ртутный слой выполнен, путем амальгамирования, в виде пленки, расположенной на дополнительном слое металла».

В таком варианте сделать устойчивую к перепадам температуры конструкции не представляется сложным. Тем не менее, для эксплуатации в условиях Земли есть необходимость все время поддерживать температуру ниже минус 38,8 оС, что достаточно неудобно и энергозатратно. Решение этой задачи дано в заявке на изобретение RU 2016 145 903 А «Движитель».

Реферат.

«Движитель является вариантом исполнения движителя Степанова, предназначенного для преобразования энергии внешнего электрического поля в перемещение тел или во вращение двигателя. На движителе образована поверхность с распределенным отрицательным зарядом, полученная без применения электрического напряжения путем использования ртути. Для получения такой поверхности используется слой, выполненный из бинарного соединения - теллурида ртути. Величина распределенного отрицательного заряда зависит от процентного содержания ртути в соединении. Равновесная структура Te*Hg при эвтектической пропорции химических элементов имеет температуру плавления 410,9 оС. Таким образом, данный движитель может использоваться как в нормальных условиях, так и при повышенных температурах».

Так как эвтектическое процентное содержание ртути в бинарном соединении составляет ~15%, то и величина подъемной силы не превысит

Fc^ = 83,3 x 0,15 = 12,5 кГ/м2

При до эвтектической процентной концентрации ртути эффект наблюдаться не будет, так как на поверхности бинарного соединения будет существовать ртуть в жидком состоянии, что нивелирует возможность связанной твердой ртути. Такая величина подъемной силы позволяет создавать летательные аппараты, перемещающиеся на высотах, соизмеримыми с их линейными размерами. То есть, когда в полной формуле кулоновской подъемной силы

90f

Fc^ = knSploplosur x J [^ + tan /(a)]2 x [cos (a)]3d(a) 0

составляющая, зависящая от соотношения ^ , имеет значительную величину.

Приведенные в статье теоретические выводы требуют экспериментальной проверки. При положительных результатах потребуется проведение многочисленных научноисследовательских и опытно-конструкторских работ для получения практических конструкций летательных аппаратов, а также иных приводных устройств.