Асимптотическая оценка затухания волнового поля в зоне каустической тени с учётом вариаций показателя преломления

переменных задачи. Это позволяет моделировать дифракционную структуру поля в зонах каустической фокусировки, учитывая как усиление поля в фокальных точках, так и экспоненциально малые поля в теневых зонах. Последние можно интерпретировать как вклады неклассических лучей: дифракционных лучей, комплексных лучей и т.п.

Если же масштаб неоднородности L меняется, сохраняя, однако, неравенство (1), требуется дополнительный анализ применимости асимптотических формул, их модификация в тех случаях, когда области пространства с разным масштабом неоднородности «накрывает» единая каустическая структура. Типичный пример – влияние неоднородностей, находящихся в классически недоступных областях (в зоне геометрической тени), на структуру дифракционного поля в этих зонах. Актуальность в исследованиях такого рода определяется необходимостью решения прикладных задач радионавигации и радиосвязи с космическими аппаратами, радиозондирования плотной плазмы и проводящих сред.

ВЕСТНИК 2014. ВЫПУСК 4

ВЕСТНИК 2014. ВЫПУСК 4

• II.    Асимптотическое описание поля волны в зоне каустики при наличии разномасштабных неоднородностей

Рассмотрим следующую модельную задачу: пусть в неоднородной среде, характеризующейся показателем преломления n(x, y, z) , в процессе распространения волны с характерным 2п волновым числом к = — (в свободном про-X странстве) формируется простая каустика – особенность типа A2 для соответствующего семейства лучевых траекторий (рис. 1). Будем считать, что условие (1) выполнено для всех рассматриваемых масштабов L вариаций показателя преломления, но масштаб L1 неоднородности в зоне света, где имеется возможность использовать понятие семейства лучевых траекторий и его огибающей – каустики, отличается от масштаба L2 неоднородности в зоне каустической тени, где классических лучей нет. Отметим, что неоднородность в зоне тени никак не влияет на геометрическую структуру каустики.

В качестве уравнения, описывающего волновое поле, возьмем следующее:

к ² n 2 ( x , y , ² ) U ( x , у , ² ) = 0, (2)

О X    О у    О 2

дополнительными условиями к которому являются: падение плоской (или квазиплоской) волны с заданного направления и условие Зоммер-фельда на бесконечности для рассеянного поля.

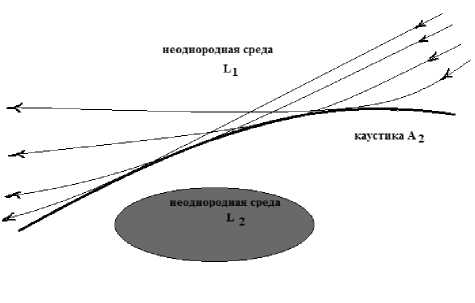
Рис. 1. Геометрия задачи

Важным в нашем рассмотрении является факт формирования каустики именно типа A2. Асимптотическое решение можно построить, используя метод эталонных функций, то есть для данного типа особенности равномерное асимптотическое решение будем искать в виде:

U ( x , y , z ) = [ ^ ( r) Ai ( X ( г)) +

+ ф (r)Ai ‘ (X ( г )) ] e k ^{( r)} .           (3)

В формуле (3) и далее используются обозначения: r = ( x , у , z ) - вектор текущих координат, Ai ( X) и Ai '( X ) - функция Эйри и её производная, определенные следующим образом:

Ai ( X ) = J exp( i ( t ³ + Xt )) dt ,       (4)

-∞

Ai ‘ ( X ) = i J exp( i ( t ³ + Xt )) tdt .      (5)

-∞

Уравнение, которому удовлетворяет функция Ai ( X ), таково:

д ² д X²

^^^^^^в

X у Ai(X) = 0.

Величинами, подлежащими определению, в (3) являются: фазовая функция S ( F ) , амплитудные функции ф ( F ) и у ( F ) , аргумент функции Эйри - X ( ^F ) .

Подставляя (3) в (2), сведя все старшие производные функции Эйри к функциям (4) и (5) в силу уравнения (6) и учитывая, что данная базовая пара функций является линейно независимой, получим следующую систему уравнений для определения искомых величин:

• k²n ² - k ²( V 5 )² + y( V X )² к +

+ ik ( ф A 5 + 2( V 5 , V ф ) ) + Аф +

+ 3 ik ( V 5 , V X ) y +

+ 3 ( ( ( V X )² + X A X ) ф + 2( V у , V X ) X ) = 0 , (7)

k²n ² - k ²( V A )² + y(V X )² J ^ +

+ ik ( y A S + 2( V A , V у ) ) + A ^ +

+ 2 ik ( V S , V X ) ^ + ( ф A X + 2( V ф , V X ) X ) = 0 . (8)

В уравнениях (7) и (8) для сокращения записи зависимость функций от F = ( x , у , z ) опущена.

Используя стандартное представление амплитудных функций ф и у в виде асимптотических рядов по параметру k ^–1 или ( kL )^–1:

+^

ф = E ф j " к - j ,                (9)

j = 0

+^

V = T^Vj- k - j ,

J=о и приравнивая члены при одинаковых степенях k в (7) и (8), получим систему рекуррентных уравнений для определения искомых величин. Первым уравнением этой системы для членов порядка k2 будет уравнение типа Гамильтона – Якоби:

к² n ² - к ² ( V 5 ) ² + X ( V X ) ² = 0 . (10)

Здесь мы учли тот факт, что решения по 5 и X не тривиальны, а значит, для разрешимости системы X ~ к2/3. Следствием этого же факта является условие:

( V 5 , V X ) = 0.

Введя обозначение:

кф = sign ⁽ X ⁾j-^ X |^2/3, преобразуем уравнение (10):

n ² - ( V 5 ) ² + sign ( X )( V ф ) = 0.

При этом sign ( X ) равен +1 для области каустической «тени» и -1 - для области «света», двухлучевой области рисунка 1. Соотношение (11) естественно переносится на функцию ф ( r):

( V 5 , У ф ) = 0. (14)

Система уравнений (13), (14) представляет собой двумерный аналог классического уравнения Гамильтона - Якоби для двухкомпонентной функции. Решение данной системы рассмотрено ниже.

Продолжая разложение уравнений (7) и (8) по степеням параметра к "1, получим с учетом (11) следующие уравнения, являющиеся аналогом уравнений переноса в методе геометрической оптики:

i ф A 5 + 2( V 5 , V ^ ,)) +

+ 6(v ,AX2 + 2(V v о, VX2)) к-1 = 0,(15)

i T j A 5 + 2( V 5 , Vф_J )) +

+ 6(^-AX2 + 2(V vj, VX2)) к-1 =-Aфj-1, j > 1

i ( у 0 A 5 + 2( V 5 , V v 0 )) +

+ ^AX + 2(V^,, VX)) к-1 = 0,(16)

i ( _V j A 5 + 2( V 5 , V v )) +

+ (фjAX + 2(V фj, VX)) к-1 =-AVj_1, j > 1(16’)

Нетрудно показать, что согласование порядков по к асимптотических членов имеет место при: Ф0 ~ к 0, Ф, ~ к - j, V 0 ~ к -1/3, Vj ~ к'3j•

• III.    Классические решения лучевого метода и особенности их продолжения в зону «тени»

Решение уравнений (13), (14), а также систем (15)-(16’) для области «света» можно получить, выразив искомые функции через известные формулы метода геометрической оптики (или метода ВКБ). В этом случае используются классические решения уравнения Гамильтона - Якоби, построенные на лучевых траекториях, получаемых из системы Гамильтона. Пусть 51 и 52 - два решения уравнения Гамильтона - Якоби в указанной зоне:

n ² - ( V 5 j ) = 0, j = 1, 2 . Их можно представить в виде:

5 j = J ( P , dr) + 5 0,.

l j

Здесь l j - j -я траектория, приходящая в точку наблюдения; для нашего случая будем считать, что j = 1 соответствует «падающему» на каустику лучу, а j = 2 - «отраженному» лучу (см. рис. 1). 5 j - соответствующий нормированный лучевой эйконал, p и г - характеристики лучевых траекторий: текущая ко_~ордината и нормированный волновой вектор, 5 _{0 j} - начальная фазовая константа определяется условием падения плоской (квазиплоской) волны.

Сравнивая (13) и (17) и учитывая (14), полу- чим:

V 51 = V 5 + Уф(19)

У 52 = У 5 -Уф(19’)

и, соответственно,

V5 _V(S1 + 52) =(Px + P2) 22

(ww X

1L 5 )₌( a,^- p ) . 22

(20’)

Решения для функций 5 и ф тогда можно выразить через эйконалы:

ВЕСТНИК 2014. ВЫПУСК 4

~~

( 5 1 + 5 ₂) п

^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^в  ^^^^^^в  ^^^^^^^^^^^^^^^^^™

51 - 52) Ф 2.

Константы интегрирования в (21) определены из условий:

и (22)

на каустике:

V                                                                     !-VI-V

X = 0, ф = 0, 51 = 52,(23)

и

Indl 2 = 1,(24)

где Indl ₂ - индекс Маслова траектории отраженного луча, что отвечает фазовому сдвигу на п

— по отношению к значению эйконала «отраженной» от каустики квазиплоской волны [8; 9]. Величина X очевидным образом определяется через ф (Г) из (12).

Заметим, что в силу соотношения (17) модули векторов p 1 и p 2 равны, и потому соотношение (14) вытекает непосредственно из (20), (20’).

Решение (21), (22) можно получить также методом «асимптотического сшивания», или методом «седловых точек» [5; 7], рассматривая асимптотику для выражения (3) в двухлучевой области, области «света».

_~ П_~оскольку в окрестности каустики разность 5 1 - 5 2 мала, для расчетов удобно использовать квадратурную формулу, следующую из (13) и

(20):

x ^                ^    ^ ²

X ( x ± ) = -     k L и ²( x ± ) Ч^ ¹^ I ( x ± ) d^

² о V V ² )

-

, (25)

ВЕСТНИК 2014. ВЫПУСК 4

где интегрирование ведется по нормали к каустике в направлении области «света» (координата x±); значение x± = 0 соответствует каустике. Формула (25) справедлива в окрестности каустики, где вектор (p1 + p2) как функция r остается ортогональным оси x±. Для продления ее действия в область «света» интегрирование следует вести по линии, на которой выполнено условие (14). Другими словами, линия аргумента X в пространстве координат (x, y, z) есть линия, всюду ортогональная вектору

^{( p} i ^{+ p} 2 ) 2

Совсем иная ситуация имеет место в зоне каустической тени, где отсутствует классическое геометрооптическое решение, так как нет действительных лучевых траекторий и действительных решений уравнения (17). Комплексифика-ция же решения (18) представляет значительные трудности при отсутствии его аналитического представления. Аналогичная проблема возникает и в методе «седловых точек». Использовать аппроксимацию зависимостей 5(г), ф(Г) и X(г) для их продолжения из области «света» в область «тени», как, например, это делается в методе локальной асимптотики [10; 5; 7], не удается, поскольку в нашем случае имеется принципиальная «разномасштабность» (L1 ≠ L2) неоднородности среды. Вследствие этого возникают значительные погрешности даже при малых положительных значениях X(г) (что отражено в приведенных ниже расчетных данных).

Однако можно получить асимптотическое представление для зависимости X ( г), учитывающее неоднородность и в зоне «тени», если вновь воспользоваться уравнением (13). Именно, качественную оценку дает формула вида (25):

, (26)

х     343 X " f X ( x f ) * + —7- k J J 2 0 у

^ A+ + p 2 + v 2 y

2 ( x f ) - n 2 ( x f ) d5vf

^    ^

S ~ ( S f+ s n - п

~     2      4 к ’

где p1+ и p2+, 5 1+ + 52 - экстраполяции зависимостей в (20) и (21), задающие также и экстраполяцию «ортогональной» линии x± в зону каустической «тени»: X(г) > 0. Если принять во вни- мание, что по нормали к каустике в направлении области «тени» волновое поле быстро затухает на масштабах X ~ 1, то при условии L2 < L1 формулы (26) и (27) можно еще более упростить:

X ⁽ x 1 ) ” ⁺

^x 1

— k f

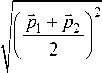
x _±=0

- n ²( x _± ) dx _±

Tk - ^1 x .=«

^*         ^*

(S ++ S +)

x _± = 0

— i^ ^S 2I x . = 0

-

(26’)

₄ ^π _k . (27’)

При значительных вариациях показателя n ( x , y , z ) в области «тени» по сравнению с областью «света», то есть при масштабе L ₂<  L ₁ (см. рис. 1), формулы (26), (26’) остаются справедливыми до тех пор, пока подкоренное выражение положительно.

Эффект проникновения поля в зону каустической тени имеет ту же природу, что и эффект проникновения квантовых частиц в классически недоступную область. Если на некотором расстоянии от каустики знак подкоренного выражения в (26) станет отрицательным, то это будет означать, что в данной области пространства уже возможно распространение квазиплоских волн и, следовательно, данная формула окажется несправедливой. Заметим, что возникновение областей, доступных для распространения волн в области каустической тени, соответствует «туннельному эффекту» для квантовых частиц. Данная ситуация не соответствует выбранной модели особенности A ₂ и здесь не рассматривается.

Определим теперь амплитудные функции φ и ψ в (3), также основываясь на формулах геометрооптического приближения в двухлучевой области. Пусть в указанной зоне, то есть в области «света», построено решение (ВКБ приближение) вида:

U ГО ( ^x , y , z ) = Z 2 = 1 X j e i ¹ , (28) где 5 , . задаются формулой (18), а х j — соответствующие решения системы уравнений переноса, возникающих в методе ВКБ и имеющие асимптотические разложения:

+^

X j = У X ,р • k ^- p . (29) p = 0

Сделаем замену, справедливую для X < 0 (и ϕ < 0):

ϕ j = A j ( - X )^1/4 ,

ψ j = 3 B j ( - X ) ^{- 1/4} ( j = 0, 1, …).       (30)

Подставляя (30) в (15)–(16’), с учетом (12) и (14) получим:

i ( A₀ A S + 2( V S , V A₀ )) -

- ( B о Аф + 2( V ф , V B 0 )) = 0,               (31)

Уравнение (33) совпадает с уравнением переноса для амплитудных функций χ_{j 0} в разложении (29). Поэтому с точностью до константы величины ( A ₀ ± iB ₀) совпадают с главными членами амплитудных функций геометрооптического приближения χ ₁₀ и χ ₂₀, и, следовательно:

i ( A j A S + 2( V S , V A j ))

^^^^^^e

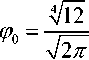
( χ 10 ⁺ χ 20 ) 2

ψ ₀ = 3

( - X )^1/4,

^^^^^^e

(B j Aф + 2( V ф, V B j )) =

⁴ 12 ( χ 10 - χ 20 )

×

^{-A A} j - 1

+

/

^^^^^^e

к

, 3^3 ф-

\ -1

×

( A j , А ф + 2( Vф , V A j - 1 ) )

+

+

/

e

к

, 3V3

Ф---

\ -2

2 π    2 i

( - X ) ^{- 1/4}

( V ф )² A j _ 1 ,

(31’)

j ≥ 1 ,

i ( B ₀ A S + 2( V S , V B ₀)) + + ( A 0 Аф + 2( V ф , V A ₀)) = 0 ,

Константы в (35) выбраны исходя из принципа асимптотического «сшивания»: ВКБ асимптотика формулы (3) в рассматриваемой области «света» должна совпадать с асимптотическим выражением (28). Сопоставление выражений для главных членов и определяет искомые константы.

Уравнения для следующих членов асимптотических разложений (9) не сводятся к их аналогам системы переноса для членов ВКБ асимптотики (29). Именно: уравнение (34) в правой

i ( B j A S + 2( V S , V B j )) +

+ ( A j Aф + 2( V ф , V A j )) =

^{-A B}j - i

^^^^^^e

зкз

\-i

--ф--- 4      2

X

x ( B j - 1 Aф + 2( V ф , V B j - i ) ) -

зкз

-ф

\ -2

(V ф)² B j - 1

,

(32’)

j ≥ 1.

Воспользовавшись здесь представл_~ением функций S ( r) и X ( r) через эйконалы S . (21), (22), преобразуем данные уравнения к виду:

( A ^ ± iB o ) A S _1-2 +

+ 2( V S 1,2 , V ( A o ± iB o )) = 0 ,                     (33)

<-w                             <-w

( A j ± iB j ) A S _t , ₂ + 2( V S _t , ₂, V ( A j ± iB j )) =

зЛ

A 3    ,3V3

= I ^{A (} A j - 1 + IB j - 1 ) - 1 — - ^ y

- 1

X

x ( ( A j - 1 + iB j-1 ) Aф + 2( Vф , V ( A j - 1 + iB j-i )) ) -

15 ( 3J3Y ,

-i-Ф^- (VФ) (Aj-1 + i7Bj-1),(34)

1ol       2 )5

j ≥ 1 .

Здесь верхний знак соответствует индексу «1», то есть характеристикам «падающей» на каустику волны, а нижний – «2», отраженной от каустики волны.

части помимо «нужного» первого слагаемого содержит члены, зависящие от величины ф ( Г) (или X ( r) ). Можно лишь утверждать, что, поскольку зависимость этих слагаемых от величины ϕ задается степенями –1 и –2, формула вида (35) будет приближенно верна и для всех j ≥ 1 при условии, что X ( r) << -1. При подходе к каустике X ( г) ^ 0 , и правая часть уравнения (34) становится неопределенной. Возникновение данной особенности связано именно с задачей выразить искомые функции через геометрооптическое решение, а оно, как известно, в окрестности каустики становится несправедливым.

Заметим, что коэффициенты исходных уравнений (15)–(16’) для членов асимптотического ряда (9) при X ( г) ^ 0 особенностей не имеют. Можно показать, что для каустики типа A ₂ расходимость амплитудных функций χ_j в представлении (29) имеет вид:

- ¹

χ j ~ X ⁴ при X → 0 , j = 1, 2;

при этом, ( χ ₁ - χ ₂) ~ X ⁴ при X → 0 .     (36)

Поэтому формулы (35) задают регулярные функции в области X ( г) <  0 .

Воспользуемся этим фактом для корректного их продолжения в область каустической «тени», где нет возможности использовать данные из ВКБ асимптотики (29), поскольку в этой области геометрооптические лучи отсутствуют. Прямое продолжение формул типа (35) «через каустику» в нашем случае невозможно в силу принятых

ВЕСТНИК 2014. ВЫПУСК 4

условий на характер неоднородности среды. Для этого, как и при определении величины X(Г) по формуле (26), сначала построим экстраполяцию зависимостей (35), а также величины X(Г) в соответствии с (12) и (22), или (25), по некоторому заданному направлению (например, x±) в зону каустической «тени»: X(Г) > 0. Обозначим соответствующие продолжения через ф0 , у+ и X+. И тогда для оценки амплитудных коэффициентов равномерного асимптотического представления (3) в зоне каустической «тени» используем следующие выражения:

+ I X I ^ф о( х > 0) ~ ^ф о I x ₊ I

,

1/4

^V о( x > о) ~ ^V о

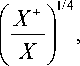
где величина X ( Г) определяется формулой (26), или (26’), и учитывает неоднородность в зоне

«тени».

ВЕСТНИК 2014. ВЫПУСК 4

• IV.    Анализ численных результатов асимптотических оценок полей в зоне каустической «тени» при наличии разномасштабных неоднородностей

С использованием формул (3), (21), (25), (26), (27), (35) и (37) было проведено численное моделирование структуры волнового поля для задачи отражения дециметрового излучения от плотного неоднородного плазменного слоя. В окрестности физической границы слоя формируется каустика типа A2. При этом в области каустической «тени» характер неоднородности существенно отличался от неоднородности в зоне «света», где градиенты электронной плотности были существенно меньше (рис. 2). На рисунке представлены: линии уровня отношения квадрата плазменной частоты к частоте падающей волны, геометрия лучевого семейства и сформированной каустики, а также линия (A–B–C–D), на которой рассчитывалась структура волнового поля.

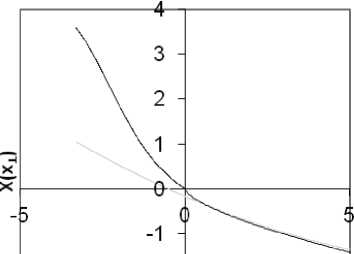
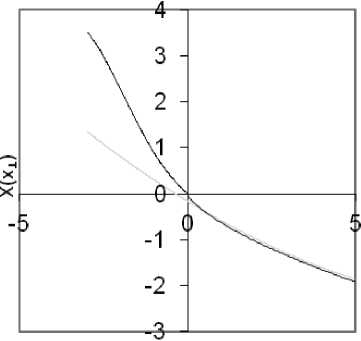
Результаты расчетов даны в серии рисунков (3–6), здесь для различных углов падения волны на плазменный слой рассчитывались: изменения аргумента функции Эйри по указанной линии «разреза», и собственно амплитуда поля (формула (3)). Представлены результаты расчета как с экстраполяцией функциональных зависимостей (20), (20’) и (35) из области «света» в область «тени» (светлые линии), так и с учетом корректировки этих зависимостей по формулам (25), (26) и (37) (темные линии). Точка «0» соответствует геометрическому положению каустики на линии (A–B–C–D), угол падения отсчитывается от локальной нормали к каустической поверхности в точке «А».

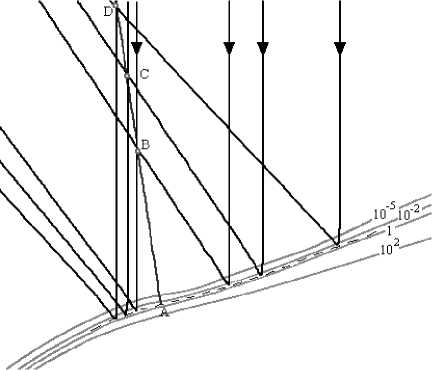
Рис. 2. Геометрия неоднородного плазменного слоя и структура лучей в зоне «света»

-----------3 J----------

Расстояние, см (0-каустика)

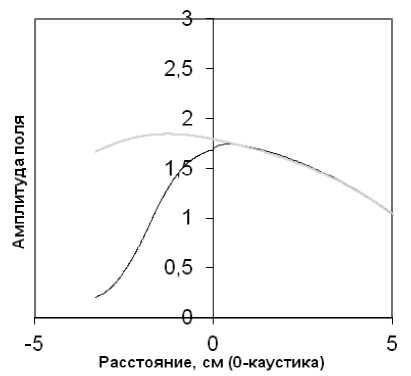
Рис. 3. Зависимость X ( Г ) и распределение поля в окрестности каустики. Угол падения - 70⁰

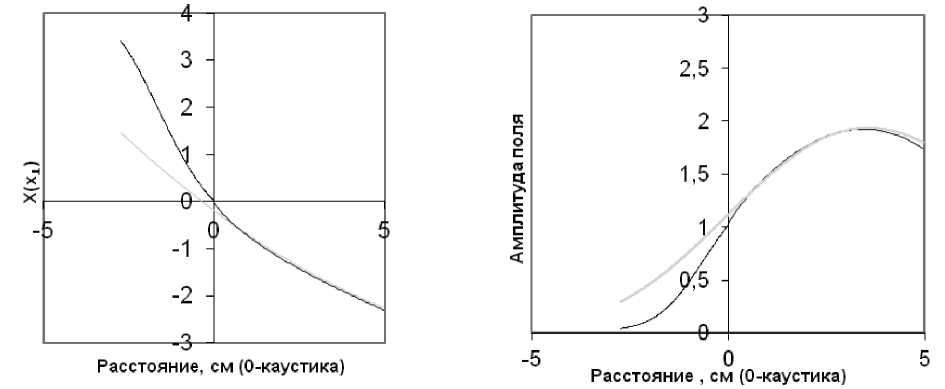
Рис. 4. Зависимость X ( r) и распределение поля в окрестности каустики. Угол падения - 40 0

Расстояние, см (0-каустика)

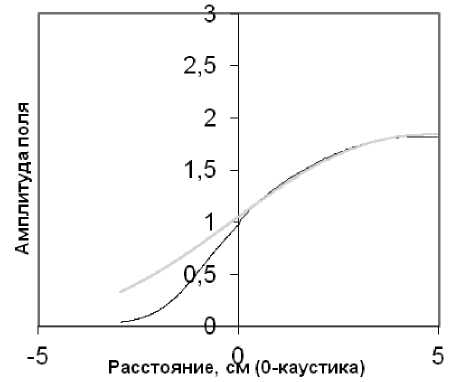
Рис. 5. Зависимость X ( г) и распределение поля в окрестности каустики. Угол падения - 50 0

ВЕСТНИК 2014. ВЫПУСК 4

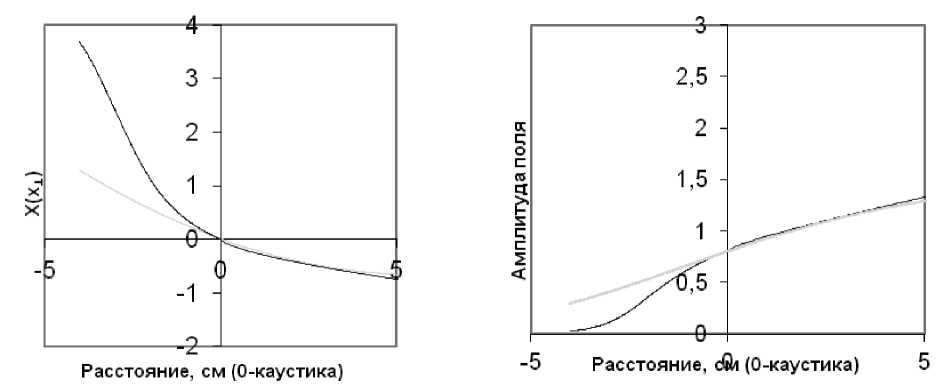
Рис. 6. Зависимость X ( г) и распределение поля в окрестности каустики. Угол падения - 80 0

ВЕСТНИК 2014. ВЫПУСК 4

Как видно из представленных результатов, корректировка асимптотических формул с учетом изменения характера неоднородности в зоне каустической «тени» дает значимое отличие результатов. Для рассматриваемого примера на расстояниях порядка глубины просачивания волны аргумент функции Эйри и ее производной в равномерном асимптотическом описании (3) имеет в два-три раза большие значения, чем те, которые определяются на основе согласования с асимптотикой геометрооптического типа (см. формулы раздела 3, или формулы метода «асимптотического сшивания», или метода «седловых точек» [1–7]). Соответственно и амплитуда поля в зоне тени имеет в разы меньшие значения. Величина этого различия зависит от угла падения волны на плазменный слой, то есть от положения геометрической каустики относительно границы слоя, но сам эффект имеется во всех случаях. При этом в области «света», вплоть до каустики, можно фиксировать совпадение результатов расчета с графической точностью, полученных как по представленным формулам, так и по любому из классических подходов построения равномерных асимптотик. Последнее является дополнительным основанием корректности применения построенных формул.

Отметим, что в расчетах наблюдается асимметрия распределения поля в зоне «тени» по углу падения волны. Это связано с имеющейся неоднородностью плазмы в продольном направлении, присутствующей в используемой модели слоя.

Заключение

Таким образом, проведенное моделирование подтверждает необходимость применения модифицированных алгоритмов расчета характеристик равномерных асимптотических формул в случае, когда характер неоднородной среды существенно меняется при переходе через каустику. Каустическая поверхность представляет собой границу областей с различным числом лучей. В рассматриваемой задаче в области «света» – два геометрооптических луча, а в области «тени» лучи отсутствуют. А поскольку полный набор характеристик геометрооптической асимптотики дает необходимую информацию для построения равномерных асимптотических выражений методом «асимптотического сшивания», или методом «седловых точек», только в том случае, когда число лучей равно кратности особенности (в нашем случае 2), информация о неоднородности в зоне, где число лучей меньше кратности недостаточна для корректной оценки поля. По-видимому, этот эффект присутствует и в случае формирования более сложных каустических структур.

Влияние различных неоднородностей в разных областях пространства, разделенных каустическими поверхностями можно проанализировать на основе метода локальной асимптотики [10; 7], но это потребует построения более сложных, чем линейные, приближений для координатных зависимостей величин в (3). Поэтому представленные в работе оценочные формулы для описания рассматриваемого эффекта являются наиболее эффективными.