Асимптотическая устойчивость однородных сингулярных систем

Сингулярно возмущенные системы обыкновенных дифференциальных уравнений применяются при математическом моделировании систем, содержащих быстрые и медленные переменные. Примером могут служить системы гироскопической стабилизации, рекуррентные нейронные сети, биологические и электрические системы и пр. Достаточно широкий обзор сферы применения сингулярных систем можно найти в работах1 [1–3].

Базовым результатом в теории сингулярных возмущений считается работа А. H. Тихонова [4], в которой были получены достаточные условия предельного перехода по малому параметру в задаче Коши. При этом также был предъявлен основной подход к исследованию сингулярных систем – декомпозиция исходной системы на систему быстрых и медленных движений. Данный подход нашел широкое применение в различных задачах исследования сингулярных систем (устойчивость, стабилизация, управление).

Обзор литературы

В рамках приложений важнейшим свойством решений сингулярных систем является устойчивость по Ляпуно- ву. Данной задаче посвящено немало работ1 [1–3]. Первой в данном направлении является работа [5], в которой исследовались, соответственно, линейные сингулярные системы вида:

x = A 11 ( t ) x + A 12 ( t ) У ,

S y = A 21 ( t ) x ⁺ A 22 ( t ) У .

и квазилинейные системы вида x = A11 ( t ) x + A12 ( t ) У + f ( t ) , ^y = A21 ( t ) x + A22 ( t ) У.

Кроме того, в данной работе рассматривались системы, допускающие выделение линейного приближения.

В дальнейшем исследования проводились в направлении нелинейных систем. В данном направлении выделено два ведущих метода, широко применяемые при исследовании нелинейных динамических систем: метод интегральных многообразий [3] и метод функций Ляпунова1. В работе данного автора представлены условия асимптотической устойчивости нулевого решения нелинейных сингулярных систем общего вида x = f (t, x, У), sy = g (t, x, У), однако данный результат неприменим к однородным системам, которые рассматриваются в настоящей статье. С задачей об устойчивости тесно связана задача стабилизации программного движения, в которой в качестве методов построения стабилизирующих управлений используются результаты решения задачи об устойчивости. В работах [6–8] были исследованы вопросы стабилизации нелинейных сингулярных систем.

Материалы и методы

В данной работе для исследования сингулярных систем с однородной правой частью применяются методы и теоремы из работы2. Приведем необходимые определения и теоремы.

Определение 1

Непрерывная функция f (x1,..., xn) называется однородной порядка µ∈ Q , если для произвольного c∈ R справедливо равенство f (CX1,_,cXn ) = c^ f (X1,_, Xn), Vx e Rn.

Однородные функции удовлетворяют следующей двусторонней оценке:

a1 x^ < f ( x)< a2x^, ai=max f (x),            (1)

Кроме того, если однородная порядка ∞ функция непрерывно дифференцируема, то ее частные производ ные ∂x также являются однородными функцi иями порядка µ- 1 , а следовательно, справедлива оценка

Рассмотрим систему дифференциальных уравнений вида

X = X " ( x ) ,            (3)

где x e R n , X ^ ( x ) - непрерывная вектор-функция, элементы которой являются однородными порядка ∞ функциями.

Теорема 1

Если нулевое решение системы (3) асимптотически устойчиво, то существует однородная порядка M, положительно определенная функция v (x), удовлетворяющая условию dv dt

= VTv(x)-X(ц)(x) = -w(x), где w (x) – однородная порядка;

( M - 1 + ц ) - положительно определенная функция.

Результаты исследования

Рассмотрим сингулярно возмущенную систему x = X д (x, y), ey = Y* (x, y),             (4)

где x ∈ R^{n 1} , y ∈ R^{n 2} ; X ^µ , Y ^µ – век-тор-функции, однородные порядка

p ц = — > 1; p, q - нечетные числа; s > 0 -q малый параметр. Предположим, что существует единственная вектор-функция ф (x), удовлетворяющая тождеству

Y ^ ( x , ф ( x ) ) = 0 , V x e R n . (5)

В силу однородности Y ^µ вектор-функция ф ( x ) должна быть однородной первого порядка. Теперь для системы (4) можно записать редуцированную систему

И V f ( x ) П ^ a 3 Н x Н ^ц , a 3 = const >  0. (2)

xc = X ^ ( x , Ф ( x ) )              (6)

и пограничную систему z = Y" (x, z + ф(x)),            (7)

где x e R n играет роль параметра. Сформулируем и докажем одно вспомогательное утверждение.

Лемма 1

Функция f (r, r2) = r1“ r2в , где а,в > 1, при r1,r2 > 0 и любом 5 > 0 удовлетворяет неравенству r1ar2' < H(5 е rf+' + 5-ar2a+').      (8)

Доказательство

Функция f ( r 1 , r ₂ ) является однородной порядка a + в и, следовательно, удовлетворяет верхней оценке

^2в < H (^ + в + r + в ) , где

H = max f (r1, r2), S = r, r,e S

= { ( r 1 , ^r₂ ) : r “ ^{+ в} + r “ ^{+ в} = 1, Г , r 2 - 0 }

.

После подстановки r 1 = 5 ² r 1 , r ₂ = 3 r₂ и сокращения обеих частей неравенства на множитель δ ^{2 α + β} , получаем неравенство (8). Методами математического анализа нетрудно получить формулу для вычисления величины H :

a

H =

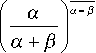
a в  ) a+в a + в J

Теорема 2

Пусть выполнены следующие условия:

Для системы (6) найдена однородная четного порядка M положительно определенная функция v, (x), удовлетворяющая неравенствам dv- = V rv, (x ). X(*).

dt (6)

.(x,ф(x))<- H X HM+"-1;

|V ^r ₄ ( x ) ■ ( X^(v ) ( x , z + ф ( x ) ) - X^(v ) ( x , ф ( x ) ) )| <

s(11)

< k, £ II x IIai ■ II z IIM+--1-ai, i=1

где k 1 , a i = const >  0, s - некоторое число.

Для системы (7) найдена однородная порядка M функция v ₂ ( x , z ) , удовлетворяющая оценкам

C 1 H z H ^M ^ v 2 ( x, z ) ^ c 2 ( н x H M + H z H M ) , ⁽¹²⁾

dv ₂ dt

= V T V 2 2 ( x , z ) • ( 7 )

Y ⁽ ^ ) ( x , z + ф ( x ) ) <- H z H M +" " 1 ,

|^{V T} v 2 ( x , zУ ^{X (} ^ ) ( x , z ⁺ Ф ( x ))| <  k 2 ^7 H x H ^p i - H z H ^M +" ^{- 1 - p} i , i = 1

V T v 2 ( x , z ) • DXx ^{( ц} ) ( x , z + ф ( x ) ) <

q

< k 3 I h z h ^M +" ^{- 1} • £ h x i r H z h M ⁺ " ^-H

I                        i = 1

где c 1 ₂ , k 1 ₂ pi, Y i = const >  0.

Тогда существует такое s >  0 , что при е <  s ₀ нулевое решение системы (4) асимптотически устойчиво.

Доказательство

Сделаем в системе (4) замену y =z+ф(x), которая сохраняет асимптотическую устойчивость нулевого решения. В результате получим более удобную для исследования систему xc = X(^) (x, z + ф (x)), z = —У(^)(x, z + ф( x ))-        (16)

£

- У^ X* ^ц ) ( x, z + ф ( x ) ) .

Доказательство теоремы будем видно, является положительно опреде-проводить при помощи функции ленной. Запишем ее полную производ- V ( x , z ) = v 1 ( x ) + v ₂ ( x , z ) , которая, оче- ную в силу системы (16):

dV dt (16)

= V ^T v 1 ( x ) • X ^{( ц} ) ( x, z + ф ( x ) ) +

+V T_x v ₂ ( x,z ) • X ^{( ц} ) ( x,z + ф ( x ) ) + — V T v ₂ ( x,z ) •

• Y ^{( ц} ) ( x , z + ф ( x ) ) -V T v 2 ( x , z ) • DDxX ^{( ц} ) ( x , z + ф ( x ) ) .

Для того чтобы оценить правую неравенствами (8; 10; 11; 13–15), в речасть выражения (17), воспользуемся зультате чего получим:

dV dt

< - II x II M ⁺ * ^{- 1} - - II z II M ⁺ * ^{- 1} + k 1 £ || x 1 Г- . || z || M ⁺ * ^{- 1 - a} i +

( 16 )                                ^e                           i =1

+ k 21 £ || x || ^e i . || z || M ⁺ * ^{- 1} - ^в + k 31 || z || M ⁺ * ^{- 1} + k 31 £ || x I r i . II z II M ⁺ " ^{- 1} - ^Y i . i =1                                                                                     i =1

Согласно лемме 1, неравенство (18) можно продолжить следующим образом:

s

< - I x I M ⁺ " ^{- 1} -I - - k 3 1 I z I M ⁺ " ^{- 1} + k i E^ ( 5 - M "  “ ‘ I x I M ⁺ " - 1 +V I z I M ⁺ " ^{- 1} ) +

(16)                         Ve       )                      i=i pq

+k2 Eh2i(5MM+"  * । x IM+"-1 +5-P1 I z IM+"-1) + k3 Eh3i(53M+"     I x IM+"-1 +5-1 I z IM+"-1), i=i                                                                                                    i=i

dV dt

где 8U, §2i, §зi > 0   - произволь ные числа; h1i,h2,,h3, в соответствии с формулой (9) определяются соотношениями

4	^      a i	a i	f M + ц - 1 - a.'	M + ц -1- a .
		\ M + ц -1 |		A m + ц -1
	. M + Ц - 1 ,	।                         । P .	v M + ц - 1 ,	J M + ц -1- в .
h 2i =	f     P i	^ M + ц -1	f M + ц - 1 - в .	^ M + ц -1
	[ M + ц - 1	j Y i	V M + ц - 1	^ M + ц -1- Y .
h 3 i=\	f      Y i	^ M + ц -1	f M + ц - 1 - y .	M + ц -1
	v M + Ц - 1	j	V M + ц - 1 ,	।

После перегруппировки слагаемых в правой части неравенства (19) получим:

spq

-V    <11 - k1 £hi^M+^-1-“■ - k2 £h2iS2M+^-1-e - k3 y§M+ ^-1-Y ■ I 11 x 11M+^-1 - dt (16)    V         i=1                           i=1                           i=1)

f                5                 pq

-I _- k 3 - k 1 £ h 1 i S 17 - - k 2 £ h 2 i S^ - - k 3 £ h 3i ^ -- 1 1 z I M ⁺ ^ ^{- 1}.

V S              i=1                 i=1                 i=1

Информатика, вычислительная техника и управление

Очевидно, что можно подобрать 5 1i , 5 2i , 5 3i , чтобы выполнялось нера-такие достаточно малые числа, венство:

spq

_{1 - k 1 ∑ h 1 i δ 1} M_i + µ -1- α i _{- k 2 ∑ h 2 i δ 2} M_i + µ -1- β i _{- k 3 ∑ h 3 i δ 3} M_i + µ -1- γ i _{> 0.}

i =1                                   i =1                                   i =1

Тогда правая часть выражения (21) становится отрицательно определен- ной при б < б0, где б0 определяется по формуле k+ks hδ-αi+kp hδ-βi+kq h δ-γi

31 _{i = 1} 1 i 1 i        2     _{i = 1} 2 i 2 i       3 _{i = 1} 3 i 3 i

Таким образом, функция V ( x,x ) при б <  б 0 удовлетворяет теореме Ляпунова об асимптотической устойчивости. Следовательно, нулевое решение системы (16), а значит, и (4) при таких значениях ε будет асимптотически устойчивым.

Теорема доказана.

Пример

Рассмотрим систему

333 x = ^- x + У 1 + У 2 ,

£ У 1 = ax ^- У 1 ,

£ y₂ = b ³ X ³ - y ³

1де a , b >  0 . Здесь ф 1 ( x ) = ax , ф ₂ ( x ) = bx .

Редуцированная система имеет вид x = ( a3 + b3 -1) x3;(25)

пограничная система имеет вид

22        23

z 1 = - 3 a x z 1 - 3 axz 1 - z 1 ,

(26) z₂ = - 3b² x² z ₂ - 3bxz 2 - z 2 .

Для системы (25) функция Ляпунова имеет вид v 1 ( x ) = x ⁴ , а для системы (26) — V ₂ ( x, z 1 , z 2 ) = Z 4 + z ⁴ + x ² z 1 ² + x ² z² . Оценки (10–15) будут выглядеть следующим образом:

dv ₁ dt

< - 4 (1 - a ³ - b ³ )| x |⁶.

|V T v 1 ( x ) ■ ( X ^{( д} ) ( x,z + ф(x ) ) - X ⁽ ^ ) ( x,ф ( x ) ))| <  K 1 (| x|³ z ³ + | x|⁴ z ² + | x|⁵ z ) ,      (27)

z4 ^ V2 (x, Z1, z2 )< |x|4 + z4, dv2

dt

<- z 6 ,

I ^ T v 2 ( x, z ) ■ X ( ^Ц ) ( x, z + Ф ( x ))| ^ K 2 (| x|³ z ⁵ +

I x |² z ⁴ + | x |³ z ³ ) ,

V T_z v 22 ( x,z ) ■ ^ФX ⁽ ^ ) ( x,z + ф ( x ) ) <  K 3 ( z ⁶ + | x|z ⁵ + | x|² z ⁴ + | x|⁴ z ²) .

где K 1 _{2 3} определяются по формулам:

K 1 = max { 4; max { a, b } ;12 V a ⁴ + b⁴

K 2 = max { 2; 6 max { a, b } ;6 V a ⁴ + b⁴

= max

4 max { a , b } ; 12 max { a , b } + 2 V a ² + b ²; 6 max { a , b } a ² + b² ;6\ a ² + b ² V a ⁴ + b⁴

.

Величины hu, h2:, h: вычислим по формулам (20):

hil   h 23   h33    2, hi2 — h22 — h32 — h34 — -3- , hi3   h21

Далее требуется подобрать такие значения ^_u , 8 2, , 8 3i , чтобы выполнялось неравенство (22), после чего остается вычислить верхнюю границу допустимого диапазона изменения параметра e по формуле (23). Поскольку K_t , ₂ , ₃ в нашем примере зависят от коэффициентов a , b , то полученное в итоге значение s 0 будет зависеть от a , b , ⁸ ii ,⁸ 2i , ⁸ з i . Коэффициенты a , b должны удовлетворять условию a ³ + b ³ <  1 , чтобы нулевое решение системы (25) было асимптотически устойчивым.

Обсуждение и заключения

Полученная теорема 2 дает достаточные условия асимптотической устойчивости однородных сингулярных систем в общем случае. Достоинством результата является возможность свести исследование исходной системы к исследованию двух систем меньшей размерности, что может оказаться полезным в силу их существенно нелинейной структуры. Соотношения (20; 22–23) позволяют количественно оценить верхнюю границу допустимой вариации малого параметра.

Условия теоремы 2 основываются на существовании однородных функций Ляпунова [9-10]. Функция v , ( x ) существует исходя из теоремы 1. Вопрос о критерии существования функции v ₂ ( x , z ) для системы (7) является открытым, а следовательно, проверка второго условия теоремы 2 требует чисто конструктивного подхода.

Все авторы прочитали и одобрили окончательный вариант рукописи.

All authors have read and approved the final version of the manuscript.