Асимптотические характеристики радоновых мер

С целю упрощения терминологии мы прибегнем к некоторому огрублению и будем говорит, что радонова мера есть разность двух локально конечных борелев-ских мер. По теореме 3.1 каждой вещественной радоновой мере μ взаимно однозначно ставиться в соответствие пара положительных взаимно сингулярных локально конечных борелевских мер и , так что . Мера называется положительной составляющей меры μ и обозначается , мера ющей меры μ и обозначается

называется отрицательной составляя-

Мера           называется полной

вариацией или модулем меры ^μ . С помощью мер , определяется ограничение меры ^μ на мно-жество по формуле

.

Отметим ещё, что на линейном пространстве , а значит и на множестве вещественных радоновых мер естественным образом вводится упорядочение Соотношение означает, что радонова мера положительна.

Мы будем рассматривать также комплексные меры Радона. Это функции множеств вида ^Н = ^Н i ⁺ i ^H 2 , где ^Н 1 , ^Н 2 - вещественные радоновые меры. Ограничение меры ^μ на множество ^Е определяется по формуле ^Н Е = ( ^{Н 1} ) e ⁺ i ^{( Н} 2 ) e . Комплексная мера Радона ^Н сосредоточена на множестве Е , если выполняется равенство ^Н = ^н е . Носитель опре-деляется и для комплексных мер Радона.

Теперь определим полную вариацию или модуль комплексной меры ^μ

. Если хотя бы одна из величин (Н 1)+( E), (Н 1U E), (Н 2U E), (Н2МE) равна бесконечности, то полагаем 1 н|(E)-+ го. в противном случае поступаем следующим образом. Назовём разбиением -множества Е такой набор борелевских множеств E1 ’'",Em, m=1,2

, ...

величину

что выполняются условия

^■;^. Тогда ,Е

E = m E k при i ^ ^k ,     k = 1 . Введём

есть точная верхняя грань числового

множества , где пробегает множество всех разбиений мно-жество ^Е .

Нетрудно проверить, что выполняются неравенства1 Н 11”1 н|, "■ “ “ , 1 pKIН1|+|Н21, и что 1р| — положительная локально конечная борелевская мера на

Несложно увидеть, что для любой функции pe^ilR1/)

справедливо

неравенство

IJ ♦ Ix I * Ы * I

^R 0 ⁿ

(supp ^ϕ )

Обозначим через Кс — это множество комплексных радоновых мер на . Отметим, что Кс является комплексным линейным пространством. В пространстве Кс вводится понятие широкой сходимости. Говорят, что последовательность радоновых мер μт широко сходится к радоновой мере μ , если для любой функции          числовая последовательность

^Н lim H m сходится к . Обозначение m ^«

Вводятся некоторые понятия множеств, связанные с пространством ^{К с} .

Множество E сК с называется широко ограниченным, если для любой функции

й>еФЦНП                         • выполняется неравенство

Множество E с с называется сильным ограниченным, если для любого г                                  sup|^|(-K) < х компакта выполняется неравенство           .

Множество EсК C называется компактным, если из любой последовательности подпоследовательность

можно извлечь широко сходящуюся

Пусть ^{р (} t )

–

некоторый уточнённый порядок. На пространстве

определяется однопараметрическое семейство преобразований Азарина

^К с ^К с , t е⁽ 0 , да) , согласно формулам

^с

А t

Ht = М ,

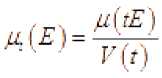
Для любого борелевского множества ^E .

n

Пусть ^{ϕ 0} . Формула переменных даёт

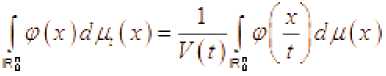
Пусть множество

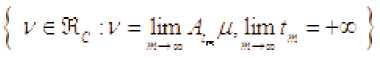
будем называть

предельным множеством Азарина и обозначим через

В случае вещественных радоновых мер наряду с предельным множеством Азарина Fr [ ^Н ] важными асимптотическими характеристиками

меры ^μ являются её верхняя конусная плотность и нижняя конусная плотность , а также верхняя плотность        и нижняя плотность

. Пусть – некоторое фиксированное число, – борелевское подмножество единичной сферы в пространстве ,

Тогда указанные высшие величины определяются следующим образом

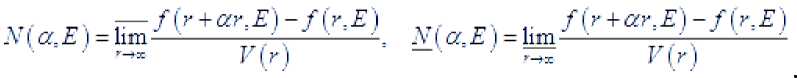
Из свойств пределов и уточнённого порядка ^{р (} r ) вытекают следующие соотношения

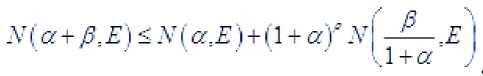
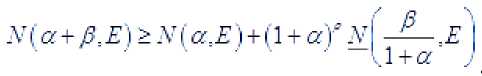
.V( ал- р.Е) > Х(а.Е )+(1 + aY -v( —— .Е I ' ^— '     ' '     ' ^— 114-й у

,

.V(a+A£)<.V(a.£)+(l + af .v| -^—.Е I ' — '     ' '     '    114-й )

, р = р ^ =lim р (r)

где           r^”.

В общем случае функция                 является не числовой функцией, а фун-кцией со значениями из расширенной числовой прямой . Поэтому в неравенс-твах (3)-(6) правая часть не всегда имеет смысл. Если в какомто из этих неравенств правая часть не имеет смысла, то соответствующее неравенство нужно считать пустым утверждением. По другому можно сказать так. Мы считаем, что неравенства, выполняются для любого.

Пусть мера μ положительна, то функция       будет возрастающей. В этом случае из равенства (4) следует, что если          конечна для некоторого а >0, то она конечна для любого а >0. Отметим ещё, что для вещественных мер из неравенств (4), (6) следует, что если функция ограничена сверху на некотором интервале (0 >^), то она ограничена сверху на любом интервале (0 ,а), а если функция " ограничена снизу на некотором интервале (0 ’^), то она ограничена снизу на любом интервале (0 ’а)

Легко видеть, что для того, чтобы обе функции

и

были

непрерывными на полуоси выполнялись равенства

необходимо

и достаточно, чтобы

limjV(#,£) = O

lim £(#,£) = О

Обозначим функцию

. Иногда мы будем рассматривать

A’[>,£:■ = И

-—,w|(r:r + (Z.’-]x£j

= Inn——----------

. (7)

Иногда возникает необходимость оценивать функцию с помощью

функций        и полезна функция

"   ~ . В этом случае наряду с функцией V ^{( r} ) = rP

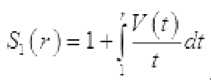
Как показывает опыт, применение функции ⁵ i^{( r} ) становится неэффективным, если эта функция является ограниченной. В случае ограниченности функции ⁵ 1^{( r} ) применяют функцию

$2    | —— dt

С помощью правила Лопиталя получаем, что

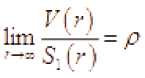
( ⁵ 1⁽ r ) — не ограничена)

Имеем

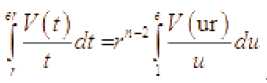
Поскольку

V ( ur )

V ( r ) ^ u ^p

r ^^ ,    u е ^[ 1 ,e ] ,

то

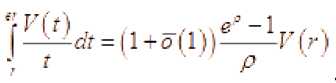
Из этого следует, что V ^{( r} Н ^{0 ( r} "^^, если ⁵ i^{( r} ) - ограниченная функция.

Вновь применяя правило Лопиталя, получим lim

( ⁵ 1⁽ r ) - ограничена)

Из этих равенств видно, что функции ⁵ i ( r ) и ⁵ 2 ( ^r ) особенно важны в случае ■ “ ' " ^_ '. В этом случае функции ^s i ( ^r ) и ^ ^{( r} ) , а также функции ⁵ 2 ( ^r ) и ^ ^{( r} ) имеют различный рост на бесконечности.

Теорема 1. Пусть ^{р ( r} ) - произвольный уточнённый порядок, ^Ц -вещественная радонова мера на , – множество из единичной сферы, ■' ~ - верхняя плотность меры Н относительно уточнённого порядка ^{р ( r} ) , причём - ' - - '- для некоторого ^а о ^{> 0} . Тогда существует постоянная M > 0 такая, что для всех ^:> - выполняется неравенство

Доказательство. Имеем

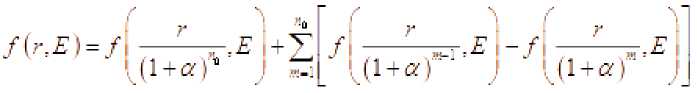
Число ^{n 0} определяется из условия

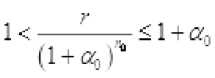
Очевидно, что существуют постоянные неравенства

м.

такие, что выполняются

/(х.ЕУ^М,

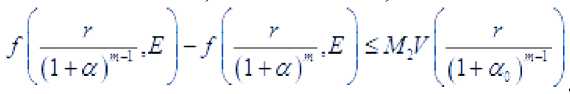
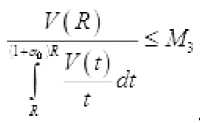
Из этих неравенств и равенства (4.10) легко следует утверждение Лемма доказана.

Применяя лемму 4.1 к мере , получим следующее утверждение

(12) леммы

Теорема 2. Пусть – множество из единичной сферы,       – нижняя плотность вещественной радоновой меры на относительно уточнённого порядка . Если для некоторого

, то существует

постоянная такая, что для всех выполняется неравенство .

Далее рассмотрим уточнённые порядки , для которых функция является ограниченной.

Теорема 3. Пусть – вещественная мера Радона на ,     –

– верхняя р (r), причём

уточнённый порядок, – множество из единичной сферы, плотность меры μ относительно уточнённого порядка для некоторогоа 0> 0 и функция ограничена. Тогда

существует постоянная такая, что для выполняется неравенство /z([?'_:oo)x£)2(>)

В данном случае

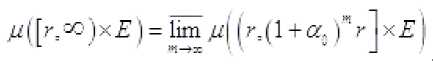
Доказательство.

Имеем

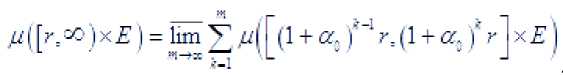
Из этого равенства и неравенств (4.11), (4.12) следует утверждение леммы Лемма доказана.

Применяя лемму 4.3 к мере , получим следующее утверждение.

–

нижняя

, уточнённый порядок, – множество из единичной сферы,       – плотность меры р относительно уточнённого порядка р(r), причём

-У(^Л)

для некоторого ^а 0 >  ⁰ и функция

ограничена. Тогда

существует постоянная такая, что для выполняется неравенство

В данном случае

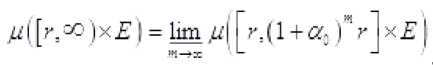
При использовании верхней и нижней плотности важную роль играют теоремы о равномерности.