Асимптотические методы для решения задач дифракции на ДОЭ

Рассмотрим дифракцию света на дифракционном оптическом элементе, обладающем зонной структурой. Свет представляет собой электромагнитные волны и поэтому строгое решение задачи дифракции должно быть основано на решении системы уравнений Максвелла с соответствующими задаче граничными условиями. Однако на практике хорошо известно, что решение уравнений Максвелла в коротковолновой области весьма трудоемкая задача даже для современных компьютеров. Для оценки поведения решения системы уравнений Максвелла в коротковолновой области широко используются асимптотические методы. Наиболее известным асимптотическим методом является приближение геометрической оптики [1]. Приближение геометрической оптики хорошо работает в случае, когда свойства среды слабо меняются на расстояниях сравнимых с длиной волны освещающего пучка. Методы решения задач дифракции на периодических структурах, основанные на точном решении уравнений Максвелла, давно известны и рассмотрены в работе [2]. Если структура не является периодической, тогда в этом случае для решения задач дифракции используются конечноразностные методы [3] или методы, основанные на решении соответствующих интегральных уравнений [4]. В данной работе рассматривается асимптотический подход к решению широкого класса задач дифракции. Подход основан на синтезе геометрооптического метода и решения задач дифракции на периодических структурах. Полученные формулы имеют прозрачный физический смысл. Для упрощения задачи на данном этапе будем рассматривать двумерную систему. Это позволит нам найти закономерности и разработать методы решения, которые впоследствии можно будет распространить на случай трех измерений для системы уравнений Максвелла.

1. Решение модельной задачи дифракции на квазипериодической структуре

Асимптотические методы в физике ассоциируются в основном с квазиклассическим приближением в квантовой механике, геометрической оптикой и вычислением интеграла Кирхгофа-Гюйгенса [5] или Кирхгофа-Котлера [6] методом стационарной фазы или методом перевала. С точки зрения физики геометрическая оптика основана на замене решения исходной задачи на решение задачи дифракции плоской волны на плоской границе раздела. Метод перевала и метод стационарной фазы [7] основаны на замене вычисляемого интеграла эталонным интегралом. Для того чтобы разработать асимптотические методы для решения задач дифракции на дифракционных оптических элементах, обладающих зонной структурой, необходимо найти и решить модельную задачу. В данной работе предложено построить целый класс асимптотических методов, основанных на решении задачи дифракции на структуре, отличной от дифракционной решетки (в пределе совпадающей с дифракционной решеткой). Модельный ДОЭ должен сочетать в себе функции расщепителя пучка (дифракционной решетки) и при этом обладать фокусирующими свойствами. В качестве модельного ДОЭ можно выбрать ДОЭ, расположенный перпендикулярно оси z в области 0 < z < a, с диэлектрической проницаемостью

£ ( x ) = Е ^£ m exP ( ikmg ( x ) ) ^{,                    (1)}

m

g(x) = g(xо) + «(x-xо) + 2P(x-xо) ,        (2)

где k - волновое число, g ( x ) - функция, описывающая зонную структуру, x ₀ – точка, в окрестности которой находится поле.

Для решения задачи дифракции необходимо найти поле в трех областях пространства:

• -    в области вне дифракционного оптического элемента со стороны источника волн;

• -    в области вне дифракционного оптического элемента со стороны, не содержащей источника волн;

• -    в области внутри дифракционного оптического элемента.

Распространение света в скалярном приближении во всех трех областях пространства описывается уравнением Гельмгольца d2 E(x, z)

-H= HE ( x , z ) ,

где E ( x , z ) - электрическое поле, а оператор H в координатном представлении имеет вид:

H =---k k 2е (x дx2         v ■

Представим решение уравнения и функцию диэлектрической проницаемости в виде

+to

е ( x , z ) = J е ( ® , z ) exp ( ik ® ( x - x 0 ) ) d ® ,        (5)

-to

+to

E ( x , z ) = J E ( ® , z ) exp ( ik ® ( x - x 0 ) ) d ® ,       (6)

-to

где ® - пространственная частота.

В этом случае решение уравнения Гельмгольца сводится к решению интегродифференциального уравнения

д² E ( ® , z )   >7 x / x

----Ц—- = J ( - k ²е( ® - n ) + k² a 2 8 ( ® - n ) )

z          -to

X E ( n , z ) d n ,

X

^е ( ® ) = Ea        ^S m exp ( ikmg ( x 0 ) )

_m \ 2n m p

( x exp

— 1

( ® - m a )

■ ik-------------

2 m p

.

Подставим выражение (8) в уравнение (7)

д² Ei®,z)                x

---= k2®2 E Uz z) - дz2                 (     )

^{- k} 2 Ea        ^e m exp ( ikmg ( ^x о ) )

„ \2 m mP

+to

: J exp - ik

-to

( ® - n - m a ) 2 m p

E ( n , z ) d n .

Для решения интегродифференциального

урав-

нения представим теперь волновое поле в окрестности точки x ₀ в виде

^E ( ® , z ) = T E s ( x 0 , z )| F s ( ® )) , s

где

x exp - ik

J       exp ( iksg ( x 0 ) )

у 2 n s p

( ® - s a )

2 s p

.

Подставив выражение (10) в интегро-дифференциальное уравнение, получим

_E d ² E » ( z )

T   dz z

')) = k '®2 T E ( z )| F (®))- n

- k² T е » - s E s ( x 0 , z )| F » ( ® )) .                     (12)

ns

Выберем некоторый набор ортогональных функций

G_m ( ® ) и умножим уравнение (12) на каждый элемент этого множества

T AmdEfez = k ² e b:e- ( x 0 , z ) - dz            _n

- k ² T aS» - E ( x 0 , z ) ,                    (13)

ns где

+to a- = (Gm (®)|F» (®)) = J G*m (®)F» (®)d®, (14)

-to

B m» = ( G m ( ® )| I ®² F » ( ® )) =

+to

= J ®2 Gm(®) F» (®) d®.

-to

В качестве примера получим асимптотики для этих матриц с помощью метода стационарной фазы

Am = i exp (iksg (x0 )) Gm (»a) ,

Bm = i exp ( iksg ( x 0 ))( Gm ( »a )( »a )2 + e) ,

где

e =

ik

2 п » в

+to

⁽ ®²G m ⁽ ® ^{) ) f} ® = » a J

-to

(- ik ® ² ) , ® exp ---- d ® +

I 2 u p J

+to

+ ¹ ( ®„ G m(® ))     f ® ² exp l- ik ® I d ® .    (18)

2 ⁽ » mV 7) ® = » a J ^1 2 s B J

-to         X “ /

При k ^ to , e ^ 0 система дифференциальных уравнений имеет вид:

^{d 2 E}» ( x 0, ^z )    ,2 (                 X

----S - = ^k ( »^a ) ^E ( x 0 , z )^- dz

- k ² E е » - s E^s ( x 0 , z ) .                              (19)

ns

Это в свою очередь совпадает с системой уравнений, полученной для периодической дифракционной решетки. Это выражение объясняет тот факт, что дифракцию на ДОЭ можно заменить дифракцией на локальной дифракционной решетке. В общем случае система уравнений выглядит следующим образом:

d ² Eⁿ x , z

-----= - k²L » E^s ( x 0 , z ) , dz ²

где ^L » = ^е » - s ^- ( A ^{- B} ) » .

Решение системы дифференциальных уравнений имеет вид

^E » ( x 0 , ^z ) =

= T ( a m exp ( ^{ik A} m ^z )⁺ b m exp (^{- ik} ^ m ^z ) ) E m ,    ⁽²¹⁾

где X m - собственные числа оператора L .

Подставляя это выражение, получим представление общего решения в виде

E(2)(to,z) = Y \— x m2ъвр xf(am exp(ikXmz) + bm exp(—ikXmz)):

/ w         (to — sa)

^{X E} m exp ( ^iksg ( x 0 ) ) exp ^{— ik}    2 s e

.

Решение в области перед дифракционным оптическим элементом имеет вид

E(1) ( to, z ) = У /——— x

* f 2nsep x (Is exp (ikV1 — to2 z) + Rs exp (— ikV1-

, x            (to — sa)

x I exp ( iksg ( x 0 ) ) exp — ik -— 2 ^

X

.

Решение в области за дифракционным оптическим элементом имеет вид

E (3)(®, z ) = У f\Ъвр

-T^s exp ( ik-J 1 - to ² z ) x

x exp ( iksg ( x 0 ) ) exp

— ik

(to — sa) 2 sp

.

Коэффициенты T ^s и R^s находятся из условия сшивки на обеих границах области 2 [8].

2. Асимптотические методы для решения задач дифракции на ДОЭ

В данном пункте рассмотрим применение вышеизложенных методов для расчета поля в случае дифракции волны на дифракционных оптических элементах, которые обладают зонной структурой. В предыдущем пункте мы рассматривали дифракцию на модельном ДОЭ. Рассмотрим теперь диэлектрический слой с диэлектрической проницаемостью, которая описывается выражением (1), где g ( x ) -произвольная функция. Случай, когда функция g ( x ) является линейной, соответствует чисто периодической структуре (дифракционной решетке). Если функция g ( x ) не является линейной, получаем дифракционную структуру с изменяющимся периодом.

Для того, что бы воспользоваться результатами предыдущего пункта сделаем предположение о том что поле в данной точке зависит от распределения диэлектрической проницаемости в окрестности данной точки. Это предположение основано все на том же принципе локализации, который был рассмотрен

выше. Далее разложим функцию g ( x ) в окрестности точки x ₀ в ряд Тейлора с точностью до членов второго порядка

g ( x ) = g ( x 0 ) + g ( x 0 )( x ^— x 0 ) + 2 g ( x ^— x 0 ) ⁽²⁵⁾

и решим задачу дифракции в окрестности точки x ₀ . Рассмотрим только поле, прошедшее через дифракционный оптический элемент (случай поля, отраженного от оптического элемента рассматривается аналогичным образом). В пространственночастотном представлении поле на выходе имеет вид

E '"(to ) = f

s

^k T s ( x 0 ) x 2 n s P

.                       (to — sa)

x exp ( iksg ( x ₀ ) ) exp — ik -— 2 ^

где ^a = g ' ( x 0 ) , P = g "( x 0 ) .

Обратимся теперь к координатному представлению. Координатное представление поля связано с пространственно-частотным представлением обычным образом с помощью преобразования Фурье

E ^{( 3 )}( x , x ₀ ) = J E ( to ) exp ( ik to ( x — x ₀ ) ) d to .     (27)

—да

Подставляем и получаем следующий вид для поля в окрестности в координатном представлении

E(3)( x,x0 ) = f Ts ( x0 )X

s

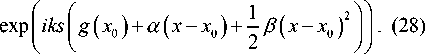
Заменяя обратно разложение в ряд Тейлора на исходную функцию, получаем, что поле в окрестности точки x ₀

^{E ( 3 )}( ^x , ^x 0 ) = f T s ( ^x 0 ) exp ( iksg ( ^x ) ) . ⁽²⁹⁾ s

Полученное выражение по форме совпадает с выражением для поля на выходе дифракционного оптического элемента, полученного в рамках метода предыскажения, рассмотренного в работе [9]. Оно также объясняет возможность использования приближения тонкого оптического элемента. Сравнивая два этих выражения, мы видим, что функция g ( x ) имеет смысл функции эйконала для геометрооптического фокусатора. Отличие состоит в том, что коэффициент T s ( x ₀ ) имеет другой физический смысл. Напомним, что в методе предыскажения T s ( x ₀ ) совпадал с коэффициентом разложения в ряд Фурье функции предыскажения. В нашем случае он определяется согласно методу, изложенному в предыдущем пункте настоящей работы.

Заключение

В данной работе разработан асимптотический метод решения задач дифракции на ДОЭ, который сочетает в себе решение задачи дифракции на периодической структуре с периодом сравнимым с длиной волны и геометрооптический подход. Решена задача дифракции на эталонной квазипериодической структуре, сочетающей в себе функции расщепителя пучка и дифракционной линзы. На основе решения эталонной задачи получено простое выражение для поля в плоскости непосредственно прилегающей к ДОЭ. Полученное выражение позволяет оценить распределение поля на выходе ДОЭ, не прибегая к сложным вычислительным методам.

Работа выполнена при поддержке гранта РФФИ 04-01-96517, гранта CRDF RUE1-005064-SA-05, а также при поддержке российско-американской программы «Фундаментальные исследования и высшее образование» (“BRHE”) и гранта INTAS 04-77-7198.