Асимптотические методы расчета поля, формируемого ДОЭ в рамках электромагнитной теории

На протяжении последних лет большое внимание уделяется расчету волнового поля, формируемого дифракционным оптическим элементом (ДОЭ). Подобного рода обратные задачи возникают при расчете дифракционных оптических элементов формирующих заданное распределение интенсивности. Эти оптические элементы получили название фокусаторов лазерного излучения. Фокусаторы используются для решения технологических проблем, связанных с лазерной обработкой материалов. Однако, в подавляющем большинстве работ задачи восстановления полей решаются в рамках скалярной теории. В данной работе задача решается в рамках электромагнитной теории.

• 1.    Постановка задачи

Данная работа посвящена задаче дифракции электромагнитного излучения на дифракционных оптических элементах. В дальнейшем для исследования свойств ДОЭ будет рассматриваться следующая оптическая схема: освещающий пучок + дифракционный оптический элемент + регистратор (рис 1). Освещающий пучок описывается распределением электрического и магнитного поля, которое наблюдается в отсутствии ДОЭ. Для полного описания свойств освещающего пучка достаточно задать распределение тангенциальных составляющих векторов электрического и магнитного поля в плоскости, непосредственно прилегающей к оптическому элементу. Регистратор представляет собой поверхность или несвязное множество точек, в которых производится измерение одной или нескольких характеристик электромагнитного поля (распределения интенсивности, фазы или поляризации поля). В дальнейшем в качестве регистратора будет использоваться плоскость, параллельная плоскости ДОЭ и отстоящая от него на некоторое расстояние.

Рис.1 Оптическая схема

Дифракционный оптический элемент состоит из подложки и области модуляции. Область модуляции представляет собой область с изменяющимся от точки к точке показателем преломления или проводимостью.

Рассмотрим прямую задачу дифракции.

Пусть освещающий пучок с заданными значениями векторов электрического и магнитного поля E,H падает на дифракционный оптический эле- мент. Необходимо найти значение векторов электрического и магнитного поля в области регистратора. Анализируя оптическую схему, можно выделить несколько областей.

• I.    Область между источником и дифракци-

• IV.    Область между плоскостью, непосредственно прилегающей к области модуляции и регистратором.

В случае ДОЭ с отражающим покрытием оптическая схема имеет другой вид. В этом случае все пространство можно разбить на две области

• I.   Область между источником и плоскостью,

непосредственно прилегающей к микрорельефу.

• II.    Область модуляции (или область микрорельефа).

• 2.    Дифракция на одномерных ДОЭ, имеющих зонную структуру

Рассмотрим дифракцию на одномерных дифракционных оптических элементах (ДОЭ), имеющих зонную структуру. Не ограничивая общности рассмотрим случай Е -поляризации. Пусть границы зон на ДОЭ описывается выражением ф ( x m ) = A m , где m- номер зоны на элементе, ф (x ) - дифференцируемая функция

Дифракционный оптический элемент представляет собой область (пластину), ограниченную плоскостями z=0 и z=h. Внутри пластины имеется распределение диэлектрической проницаемости (показателя преломления), которое описывается функцией е ( x, z ). В пределах каждой зоны можно записать разложение в ряд Фурье

е ( x , z ) = n =£ e mn ( z )exp f i2* — xm ) 1 ,      (1)

n =—^          V d m )

где d = xm+1 — xm , xm - левая граница зоны, xm+1 -правая граница зоны.

Учитывая выражение (1), можно написать разложение в области пластины в следующем виде

^{е (} x , z ) = Е Е ^е п ^{( x} , ^{z )e} xp f i ^2mT ( x x^m ) ^{1      (2)}

m n =—ю           V d m )

где e n ( x, z ) - кусочно-постоянная функция по переменной x .

Для размера зоны d_m можно написать прибли-

A женное выражение dm =------. Подставляя это ф'( xm)

выражение в (2), получаем онным оптическим элементом.

• II.  Область подложки.

• III.    Область модуляции.

n =го

^{£ (} x , z ) = E E ^£ n ^{( x} , ^z ) ^x m n =-го

(2nni       ( x expl —— ф (xm )(x к A

xm

) }=

n =ГО

= E E ^e n ^{( x} , ^z ) ^x m n =-го

Решение полученной системы уравнений представляет достаточно сложную математическую задачу. Поэтому, чтобы упростить задачу, положим ⁵ E n ^{5 2} У n n „   _ ZX ZX _a

---® 0 и —— ® 0. В этом случае система уравне- d x        d x ²

ний в частных производных превращается в систему обыкновенных дифференциальных уравнений

I 2nni / x expl----(mA + ф (xm)(x к A

Учитывая разложение в ряд: ф ( x ) = m A + ф ( X m )( X - X m ) ,

предыдущую формулу приближенно можно переписать в следующем виде n=го е (x, z) = E £n (x, z )exp(ikпф( x))                (5)

n = -ГО

Проводя аналогичные рассуждения, можно записать аналогичные разложение для поля внутри области модуляции n = го

E (x, z) = E En (x, z )exp(ikao x + iknф( x)),(6)

n= -ГО отраженного от ДОЭ n=ГО

E (x, z) = E Rn (x, z )exp(ika0 x + iknф( x))

n=-ГО и прошедшего через ДОЭ n=ГО

E (x, z) = E Tn (x, z )exp(ika0 x + iknф( x)).(8)

n =-го

Распространение электромагнитной волны в случае Е- поляризации описывается уравнением Гельмгольца [1,2]

^- E + ^4 + ^{к 2} е ( x , z ) E = 0                (9)

d x ² d z ²

Подставляя (5), (6) в (9), получаем уравнение

E^AE n (x, z) + 2 ikVEn (x, z) V Уп (x) + n=-го

+ ikE n ( x , z) Ay n ( x ) - к ² E n ( x , z ) ⁽ V y ( x ) ^{) 2} ) x (10)

x exp(ikyn (x)) + EEk 2 £s(x,z) Es(x,z)x sl x exp(sф(x) + yi (x))

Далее умножаем правую и левую часть полученного равенства на exp( - ik y p ( x )) и интегрируем по апертуре.    Учитывая, что при k ^го

J f (x) exp(ikyi (x))dx ^ 0, получаем систему диф ференциальных уравнений в частных производных

( A E_n ( x , z ) + 2 ik V E_n ( x , z ) V y _n ( x ) +

+ ikE n ( x , z ) A y _n ( x , z ) -

- k ² E n ( x , z ) ( V y ( x ) ) ² ) +                         ⁽¹¹⁾

+ E k 2 £ - 1 ( x , z ) E i ( x , z ) = 0

i

I-,2^                                     Л

-----n 2    ^{+ k 2} E n ^{( x} , ^{z ) (v} У п ^{( x ) ) 2 +}

¹ J z ^{2                          J} (12)

+ E k ² £ n - 1 ( x , z ) E l ( x , z ) = 0 1 =-rc

Рассмотрим теперь распространение поля вне области модуляции. Для примера рассмотрим распространение волны, прошедшей через область модуляции. Пусть прошедшее поле при z=0 имеет вид

ET(x) = nE ETn(x)exp(ikny(x))

n =-rc

Представим решение в пространстве виде n =^

ET(x,z) = E ETn(x,z)exp(ikny(x,z))

n =-ю

Подставляя это выражение в уравнение Гельмгольца для однородной среды, получаем n=?(AETn (x, z) 2

E ----7--- + tV ETn (x, z) x n=-»(    k2

iT xVyn (x, z) + -E n (x, z )Ayn (x, z) - k

- E^T n ( x , z ) ( v У п ( x , z ) ) ² +

+ £ 3 E^T n ( x , z ) ) exp ( ik y _n ( x , z ) ) )

Умножая полученное равенство на exp(- ikyp (x, z)), интегрируя по переменной x и ис пользуя предельные свойства при k ^ го, получаем дифференциальное уравнение в частных производных первого порядка

^(v y p ^{( x} , ^{z ) ) 2} = ^£ 3 ⁽¹⁶⁾

Для дальнейших рассуждений нам потребуется выражение для нормальной производной поля на границе однородной среды и области модуляции. Это выражение имеет вид a ET n(x, z)

+ d z

к

d E^T ( x , z ) = ⁿ =”

^d z  = n Ъ

+ ik ^ Уп (x, ) ETn (x, z) | exp(ikn y„ (x, z d zI

При k ^ го это выражение приобретает вид d ET (x, z) _ n=гоГ dyn (x, z) ------------— / l ikx d z      n =-гок      d z(18)

x E_n^T ( x , z ) exp ( ikn y _n ( x , z ) ) )

Нетрудно заметить, что при z=0 это выражение имеет вид aET(x) n=”          faVn(X))

= ik- £ -II x d z   nF  F I d x J (19)

V x EnT (x) exp(ikn vn (x)))

Аналогичные выражения можно написать для поля, отраженного от ДОЭ и его нормальной производной

мостью s (x )). Рассчитаем эквивалентный ему дифракционный оптический элемент, у которого показатель преломления принимает только 2 значения, например, 1 и £ _max. Эквивалентность здесь пони-

мается в смысле эквивалентности поля, создаваемого данным оптическим элементом. Согласно резуль-

n = K>

E R ( x ) = Z E Rn ( x , a )exp ( ikn v _n ( x ) ) n =— to

a E R ( x )_ ⁿ-          fa V n ( x ) ) _x

= — ik-x £ — II x d z nF V d x J (20)

V x EnT (x, a) exp(ikn vn (x)))

Представим решение системы уравнений в виде

E n ( x , z ) = Z E^T m ( x ) E nm ( x , z )                (21)

m

татам, приведенным в предыдущем пункте, это означает, что мы должны построить бинарную функцию, Фурье-коэффициенты которой совпадают с коэффициентами исходной функции. Точное решение данной задачи не существует, поэтому построим функцию, у которой первые n коэффициентов Фурье совпадают с некоторой точностью.

Описанный метод основан на теории эффективных сред [3,4,5 ]. Легко показать, что для этого каждый отсчет функции необходимо заменить решеткой

с периодом, намного меньшим длины волны, и коэффициентом заполнения, полученным из следую-

где E_nm ( x , z ) решение, удовлетворяющее при z=0

щего соотношения:

^£ = ^£ max ^{f + (} d ^{— f} )

граничным условиям

E nm ^{( x} , ⁰⁾ = ^ nm ,

dE nm ( x ,0) dz

= ik, 1

^^^^^^B

d V n dx

^ nm

При данном выборе базовых решений автоматически удовлетворяются условия непрерывности при z=0.

Поле внутри оптического элемента представляется в виде

E(x,z) = Z ZTm (x)Enm (x,z) exp(ik Vn (x)) , (23) nm поле в области I при z=0 имеет вид

E ( x ,0) = exp ( ik v 0 ( x ) ) +

где d- период решетки, f- длина заполненной диэлектриком части периода (рис.2). Нетрудно заметить, что при уменьшении периода дифракционной решетки точность решения увеличивается. В качестве примера рассмотрим дифракционный оптический элемент, фокусирующий в линию (рис.3). В этом случае дискретизованная по координате функ-

ция диэлектрической проницаемости имеет вид:

^£ bin ⁽ x ) = ^£

max

Z F ^{( x — x} n , ^f n ^)x

n x rect(x, xn, xn+1)

n =rc

⁺ Z R n ^{( x)ex} P ^{( ik} V n ^{( x} )),

n =—rc

его производная

^-—^{( x} ^) = ik^ 1 — а ² exp ( ik a x ) — d z                       '

—

n =to

Z ^ik i ¹

—

^d V n ^{( x} ) ) 2

n =—to

d x

R_n ( x ) exp ( ikn v _n ( x ) )

Приравнивая значения поля и его производной при z=-a, получаем систему уравнений для определения функций R_n ( x ), T_n ( x ) . Полученная система линейных уравнений с точностью до обозначений совпадает с системой уравнений для определения дифракционных коэффициентов для диэлектрической решетки, период которой равен размеру зоны на дифракционном элементе в точке с координатой x.

Рассмотрим дифракционный оптический элемент, представляющий собой плоскопараллельную пластину с изменяющимся по апертуре показателем преломления n ( x ) (или диэлектрической проницае-

^ ( x ) =—V x ² + f ² 0 , £ ( x ) =1 ----- V max

2 mod 2 ^ ^{( x} ) |

X hmax =   ----высота бинарного микроре лье-

^£ max

фа, £ max -диэлектрическая проницаемость мате-

А(£(x„ )— 1)

риала микрорельефа, f n = ^{х х} “'—- - степень за- ^£ max ^{— 1}

полнения диэлектриком, А -период бинарной дифракционного решетки, формируемой в каждом отсчете, f ₀ -фокусное расстояние.

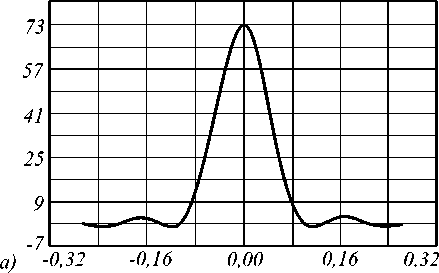
Результаты расчета поля приведены на рис.3.

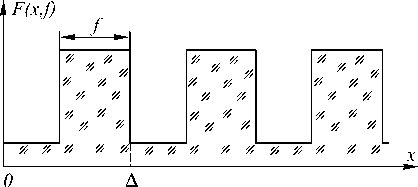
Рис.2 Профиль решетки в каждом отсчете

I д

x

A = k I 0

+ ik

^д у

f о 1 1 V- 1 о J ,

£

V

- 1

1 f д х 0 1f- д у ik V 0 д у 1V- д у

+ ik

£

A

^^^^^^B

V

£ J

- 1

£

- 1

J

^^^^^^B

д х 1 д 1 x

д у д у

д x

д х

+

+

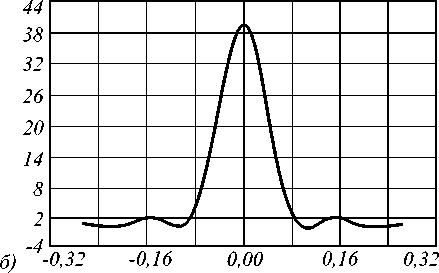
Рис.3 Поле от фокусатора в линию а) f=100мм, D=10мм, б) f=10мм, D=10мм

Для решения данного класса задач необходимо знать законы преобразования бивекторов. Пусть линейное преобразование координат в плоскости (x , y) имеет вид

^x 1 = f P 11 P 12 Y ^x ' . у J V P 21 p 22 JV у'.

x,у -старые координаты, x ', у ‘ - новые координаты.

В этом случае закон преобразования бивекторного

3. Дифракция на двумерном ДОЭ, имеющем зонную структуру.

3.1 Уравнения электродинамики, для тангенциальных компонент

Систему уравнений Максвелла запишем в следующем виде:

d E„ = - д 11 (д Hv - д Hx )l + UH, zx x x y yxy k V £J дEv = -дI1 (дHp -дHx)|-ikHx, zy y xy yx x k V £                J(26)

5 z H x = v д x ^у - 5 _y E x ) — ik s E _y , ik

5 z H y = -k д у ( д_хЕу — д у Е х ) + -k ^ E x •

Для удобства дальнейшего анализа перейдем к операторно-матричной форме записи уравнений. В операторной записи система уравнений Максвелла имеет вид

поля имеет вид f W1( x, у, z) "

W 2 ( x , у , z )

^W > ( ^x , ^у ,z)

V W4( x, у, z) J f P11 P12

= P 21 P 22

V

p ₁₁

p ₂₁

If W 1 ( x ', у ', z ) 1

W 2 ( x ‘ , у ', z )

д _z W = HW

где W - матрица-столбец из 4-х компонент

f E x 1

W =

E y

H x

V

H

у J

H -блочно-матричный дифференциаль-

ный оператор f A 01f 0

H = 1

0 B 1

p ₁₂

p ₂₂

W 34 ^x' , у;^z ) JV W 4 ( x ‘ , у ', z ) J

Закон преобразования бивекторного поля вытекает из закона преобразования двумерных векторов.

3.2 Дифракция на двумерной зонной структуре

3.2.1 Решение в области неоднородной среды

Рассмотрим дифракционный оптический элемент, представляющий собой плоскопараллельную пластину, с показателем преломления, имеющим следующий вид

£ ( x , у , z ) = n ^ £ n ( x , у , z )exp ( ikn Ф ( x , у ) )        (31)

n =-rc

Представим бивекторное поле в аналогичном виде n =rc

W ( x , у , z ) = ^ W n ( x , у , z ) exp ( ikn Ф ( x , у ) )      (32)

n =-rc

Подставляя (31), (32) в (27) или (28), получаем систему уравнений

^ех р ( '* ^ф n ) 5 z E xn = 7 exp ( zA O n + m ) • k

• '^d x ^S m ^[(d x H ny - ^d y H nx ^{) +}

• +    ik ( H ny 3 x Ф n - H nx d y Ф n ) ] +

• ⁺    ik S m 5 x ^ф n ₊ m ^[( 3 x^H ny ^- 3 y H nx ^{) +}

• +    ik ( H ny 3 x Ф n - H nx 5 y Ф n ) ]

• ^{+    S} m 1 ^d x ^[(d x H ny  ^d y H nx ^{) +}

• +    ik ( H_nv8_x®_n - H_{n Х}3„Ф„) ] } ny x n nx y n

• +    ikH ny exp ( ik Ф _n )

exp ^{( i}^ n ) s z E yn = i ^e xp ⁽ ik ® n + m k k

• '^d y ^S m ^[(d x H ny ^-d y^Hnx ^{) +}

+ ik ( H ny d x Ф n - H nx d y Ф n ) ] +

⁺ ik ^ m ^(d y ^ф n + m ) [ ^(d x^Hny ^{- d} y^Hnx ^{) +} (33)

+ ik ( H ny d x ф n - H nx d y Ф n ) ] +

^{+ S} m 1 ^d y ^[(d x H ny  ^d y H nx ^{) +}

+ ik ( H_nv8_x®_n - H_{n Х}5„Ф„)]}- ny x n nx y n

- ikH„„ exp ( ik Ф „) nx         n

A ns	i = 7 k	f ik ЗуФ„ xn IL     0	0 I ik d y ф n 7
-1		f- ik d y Ф	s ik d x Ф s I
x S 1	n - s	I	I +
		L - ik y Ф s   ik 3 x Ф s J
	f	0 1 J
+ ik5
L		- 1 0 J
	1	f ik d x Ф n	0 I
I? =			Ix
ns	ik	IL 0	ik 5 y ф n J
x 5	f-	ik ЗуФ, ys	ik d x Ф s I         f 0 - 1 1 + ikSn_ c I
n , s	L-	ik 3,,Ф, ys	ik d x Ф s J         s L 1 0

В частном случае когда d y Ф = 0

A	ns	_	- ik	x
x	IIf ^^^^^» L	0 5 ns		S - 1 n -	,5 ф 5 ф -8 । s x n x s    ns 0 J	•	(37)
B	ns	_	- i k ।	0 - S n	3 ф 3 ф 8 x n x s ns - s               0	+ S n - s I	(38)
Hns		_	- ik	f 0 LB ns	A ns 0 J		(39)

В этом случае система уравнений распадается на

^ex P ^{( i}^ n z^Hxn = 7^ex P ^{( ik Ф} n ) • ik

• ik ( д_хФ„ ) [( д E_nv -d _V E „_x) + x n x ny y nx

^{+ ik (} E ny ^d x ^Ф n ^- E nx ^d y ^Ф n ^)]

^{+ d} x ^[(d x E ny ^{- d} y E nx ^{) +}

+ ik ( E_{n у}д_хФ_н - E_{n х}дуФ_н) ] )- ny x n nx y n

^- ik S m E ny e ^{xp (} i ^{k Ф} n + m )

две независимые системы

d

z

E x

H y

=E

s

L

-

n

S

- 1

n - s

а ф а ф x nx

s

-

5 ns

E x

^S n - s

J

H y

s

^ex P ^{( ik Ф} n ) 5 z^Hyn = 7^ex P ^{( ik Ф} n ) • ik

• ^{{ k (d} y ^Ф n 7 x^Eny ^-d y^Enx ^{) +}

^{+ ik (} E ny s x ^Ф n ^- E nx ^d y ^Ф n ^{)] +}

^{+ d} y ^[(d x^Eny ^-d y^Enx ^{) +}

+ ik ( E_nv d_ХФ_n - E_n ^.ЗуФ^ ) ]}- ny x n nx y n

^- ik S m E nx ^{exp ( ik ф} n + m )

d

z

E y

H x

=E

s

n

-

5 ns

E y

9 Ф 9 Ф 8

x n x s ns

^{+ S} n - s

H x

s

3.2.2 Решение в свободном пространстве

В свободном пространстве выражение ( 35) име-

ет вид:

A ns

В данных формулах везде предполагается суммирование по повторяющимся индексам

Умножая полученные уравнения на exp ( ik Ф _s ) , интегрируя по переменным x, y и отбрасывая члены o | — | , получаем выражение:

I k J dzWn (x, y,z) = E Hn,s (x, y,z)Ws (x, y,z)     (34)

s

^H n, s ⁽ x , y, ^z ) =

_r A _ns ( x , y , z )       0     Y0 1 'I,           ⁽³⁵⁾

I 0         B ns ( x , y , z ) JL 1 0 J

i । ikd x Ф n       0 J k L 0     ikd y ф n Jx

f- ikд,,Ф,  ikЭ„Ф^    00 Pl ys xs x| , _           _ 1 + ikI 115,,

I - ik „Ф,   ikдхФ5 I I-1 0 J ysxs

[ 1 f ik d _x Ф _n      0    'I

^{B ns} = [ ik L    0      ik d y ф n

f- ikд,,Ф, ikЗуФ, । fo ys xs x I                                 I + ikI

I- ik дуФ, ik 3_ТФ, I 11 ys xs

Поле в области I имеет вид

W ( x , y , z ) =

где

n _Ю

= E W n ( x , у , z )exp ( ikn Ф ( x , y ) )

n _-Ю

W n ( x , у , z ) = § n 0 ( l n ^e ( x , у ) W ^e ( a n , P n ) + + I hn ( x , у ) W ^{+ h} ( a n , P n ) ) x

(:

x exp l ik -^1

2   2 2 l an - Pn z l +

■ k e ( x , у ) W ^{- e} ( a n , P n ) + + R nh ( x , у ) W ^{- h} ( a n , P n ) ) x

плоскости так, что направление оси х совпадало с градиентом функции Ф ( x , у ). В этом случае а у ^{ф (} x , у ) .

В новой системе координат падающее поле имеет вид

W '( x ', у ') = P ^{- 1}W ( x , у )                         (51)

x exp l - ik J1 -

a n ²

P n 2 z

I W\ W ± e ( a , в ) =

+ V1 - a ² - P ² a

+ J 1 - a ² - P ² P

,

к

в

- a

J

- P

| W W ± h ( ав ) = ^

a

1 - a

^^a P ² P,

IW = If           V =t ■

V ( 2 - a ² - P ² )( a ² + P ² )

Поле в области IV имеет вид

W n ( x , у , z ) = ( TV ( x , у ) W ^{+ e} ( a n , P n ) +

+ T hn ( x , у ) W ^{+ h} ( a n , P n ) ) x

(p( 9 )   Е_г )         fcos ^ - sin #)

P = K^{V v 2} l p( 9 ) = l               l (52)

к E ₂    p ( 9 ) J        к sin 9 cos 9 J

W ' ( x ‘ , у ') = ( cos 9 I^e - sin 9 I^h W^e 0 +

+ ( sin 9 I^е + cos 9I^h ^^h 0

В новой системе координат прошедшее электромагнитное поле будет иметь вид n =^ /

W'(x ‘, у') = ^(Tne (x ‘, у') X n=-rc

X ( cos 9 I^e - sin 9 I^h ) w ^{+ e} ( a n ,0) +

+ Thn (x', у') (sin 9 Iе + cos9Ih )w+h (an ,0))x x exp(ikn Ф( x', у'))

к ⁵ _у Ф|

⁹ = ^arc tg\       l ^a n = ^{n d} x ^{,ф( x} ', у ')

(d x Ф J

Id x '| I cos 9 sin 9 |Id x

(d _у - J (- sin 9 cos 9 J(d _у

Поле в старой системе координат имеет вид

W ( x , у ) = PW ' ( x ', у ')                            (54)

X

¹ - ^an ²

P n ² z ^| ,

Электромагнитное поле в области 4 вычисляется с помощью интеграла Кирхгофа-Котлера [1,2]

где ^а п = a x ^ф n , P n = а у ^ф n , ^ф n = n ^{ф (} x, y ),

W ₀ ± ^e = W ± ^e (0,0) = '

I -I 0

j E =      J-[ n , H ] + [ ? 0 , [ n , j E ]] -

4n s                                         (55)

- ( [ n ,/ H 1 r „ ) _? 0 Pp rkr ) ds

_ к

1 J

W_o ± ^h = W ± ^h (0,0) =

I ⁰ J

+ 1

к ⁰ 7

•H = 4 П Ш» , E ] + [- » , [ » . ^H 1+ s

+ ( [ « , E ? ]■ ^r 0 r 0 j exp rikr ) ds

В матричном виде интеграл Кирхгофа-Котлера

Используя непрерывность тангенциальных

ком-

понент на передней и задней грани дифракционного

оптического элемента, можно получить выражения для коэффициентов отражения и прохождения света. Полученная система линейных уравнений совпадает с системой линейных уравнений для определения коэффициентов дифракции на одномерной периодической решетке. Направление штрихов определяется вектором ( -Ф у , Ф _x ) .

имеет вид

W ( x ) = -i l Г ^exP ^{( ikr} ) T ( x , x ') W ( x ') ds 4 n⁵    r

s

T ( x , x ') =

3.2.3 Поле на выходе дифракционного оптиче ского элемента

Пусть падающая электромагнитная волна описывается выражением

W ( x , у ) = I^eW 0 ^{+ e} + I h W ₀ ^{+ h}                  (50)

найдем выражение для поля в точке с координатами (x,y). Для этого повернем систему координат в

^{- r} 0 z       ⁰

0       - r0 z r0 уг0 x   1 - r 20 x r20у - 1 - r0xr0у

^{- r} 0 у^г 0 x ^r 20 x ^{- 1}

^{1 - r} 20 у   ^r 0 x^r0у

- r _{0 z}       0

^{0        - r} 0 z

,         ,        ,          , r

*         *        *          *

r = ^{x - x} , ^r 0 = _H ^r

^r =l^—l

3.2.4 Поле от радиально-симметричного оптического элемента

Поле на выходе радиально-симметричного оптического элемента в полярных координатах при нормальном падении плоской волны имеет вид

n =x

W(p, 9) = ^(Tne (p) X n=-X x (cos 9Ie - sin 9Ih )w + e (an ,0) +

+ Thn (p) (sin9 Iе + cos9 Ih )W+h (an ,0))x x exp(iknФ(p)), аП = n

d Ф ( p ) d p

W ( p,^^

' Ep'

E ⁹ _H ^p

I ^H 9 )

Закон преобразования бивектора от декартовых координат к полярным имеет вид

' E x 1

E y

Hx

v

H

У )

' cos 9	- sin 9	0	0 i	' E p 1
sin 9	cos 9	0	0	E 9
0	0	cos 9	- sin 9	H p
v 0	0	sin 9	cos 9 ?	V H 9 )

Подставляя полученное выражение в (60) и вы-

числяя интеграл (56), получим электромагнитное поле, формируемое радиально-симметричным опти- ческим элементом.

В качестве примера приведем результаты расчета плотности потока энергии (вектора Умова-Пойтинга) от бинарного, радиально-симметричного оптического элемента, функция диэлектрической проницаемости которого вдоль радиуса задается выражением (25). Оптический элемент освещался Гауссовым пучком. Результаты расчета представлены на рис.4.а и 4б.

На рис 4в и 4г представлено распределение плотности вектора Умова-Пойтинга в фокальной плоскости неосевого сегмента фокусатора при освещении гауссовым пучком. В случае, изображенном на рис 4в использовался неосевой сегмент, у которого пространственная частота и направление зон изменялись достаточно слабо. В примере, изображенном на рис 4г был выбран неосевой сегмент, частота зон которого изменялась в пределах от 3.6 мкм до 8 мкм. Полученная форма распределения энергии объясняется существенным различием коэффициентов пропускания в различных точках апертуры ДОЭ. Это привело к сильной амплитудной модуляции поля на выходе ДОЭ. Это в свою очередь отразилось на структуре фокального пятна.

4. Заключение

Приведенные результаты наглядно показывают, работоспособность предложенных в данной работе методов и алгоритмов вычисления поля, формируемого дифракционными оптическими элементами в рамках электромагнитной теории. Простота и на- глядность полученных формул позволяет применять их для оценки качества работы ДОЭ в инженерных расчетах не прибегая к точному решению системы уравнений Максвелла.

г)

а)

б)

в)

Рис. 4. Поле от бинарного, радиально-

симметричного оптического элемента.

а) f=100мм, D=10x10мм; б) f=50 мм, D=10 x10мм;

в) f=20мм, D=10 x10м; г) f=20мм, D=10 x10мм