Асимптотические поля напряжений у вершины трещины в идеально пластическом материале в условиях смешанного нагружения
Автор: Степанова Л.В.
Статья в выпуске: 3, 2020 года.
Бесплатный доступ
В статье представлены асимптотические поля напряжений у вершины трещины в идеально пластическом материале в условиях смешанного деформирования для плоского деформированного и плоского напряженного состояний. Цель исследования обусловлена необходимостью построения аналитического представления поля напряжений в окрестности вершины трещины для всего диапазона значений параметра смешанности нагружения, характеризующего тип смешанного деформирования. Вид смешанного деформирования задается параметром смешанности нагружения, изменяющимся от нуля, что соответствует поперечному сдвигу, до единицы, что отвечает нормальному отрыву. Решение статически определимой задачи отыскания поля напряжений у вершины трещины получено методом разложения по собственным функциям. Найдены распределения напряжений в полном диапазоне смешанных форм нагружения от нормального отрыва до поперечного сдвига. Показано, что решение описывается различными функциональными зависимостями в разных секторах (в семи секторах - при нагружениях, близких к поперечному сдвигу, в шести - для значений параметра смешанности от 0,33 до 0,89, и в пяти секторах - при нагружениях, отвечающих значениям параметра смешанности нагружения, больших 0,89 для плоского деформированного состояния; в семи - от 0 до 0,39, пяти - от 0,39 до 1 для плоского напряженного состояния). Интересной характерной чертой полученного асимптотического решения является наличие диапазона значения параметра смешанности нагружения (от 0,89 до 1) для плоского деформированного состояния, при котором решение имеет вид распределения напряжений при нормальном отрыве. Следовательно, для плоского деформированного состояния существует такой диапазон значений параметра смешанности нагружения, при котором асимптотическое решение описывается соотношениями, не зависящими от значения параметра смешанности нагружения из этого диапазона, и соответствует чистому нормальному отрыву. В случае плоского напряженного состояния такой диапазон отсутствует и решение отражает любое значение параметра смешанности нагружения. Полученное асимптотическое решение задачи может рассматриваться как предельное решение для материала, следующего степенному закону деформационной теории пластичности или степенному закону Бейли - Нортона.
Трещина в идеально пластическом материале, статически определимая задача, секториальное решение, степенной закон деформационной теории пластичности, смешанное деформирование, параметр смешанности нагружения, аналитическое решение, асимптотическое решение
Короткий адрес: https://sciup.org/146282007
IDR: 146282007 | УДК: 539.3 | DOI: 10.15593/perm.mech/2020.3.08
Текст научной статьи Асимптотические поля напряжений у вершины трещины в идеально пластическом материале в условиях смешанного нагружения
ВЕСТНИК ПНИПУ. МЕХАНИКА № 3, 2020PNRPU MECHANICS BULLETIN
Несмотря на то, что изучение полей напряжений у вершины трещины в идеально пластическом материале восходит к работам Прандтля [1] и является классической проблемой механики упругопластического разрушения, вопросы определения напряженно-деформированного состояния в жестко идеально пластическом и упругом идеально пластическом материале продолжают вызывать интерес в научном сообществе, особенно в связи с необходимостью математического описания полей напряжений у вершины трещины в условиях смешанного нагружения в материалах с нелинейными определяющими уравнениями [2–14]. Результаты исследований [2–14], полученные в самое последнее время и касающиеся более точного и аккуратного описания напряженно-деформированного состояния вблизи вершины трещины в упругопластических материалах, опираются на теоретические, экспериментальные и численные решения, ставшие уже классическими результатами нелинейной механики разрушения [15–23]. Например, в статье [2], где исследуется возможность распространения имеющихся асимптотических решений двумерных задач для идеально пластического материала на трехмерный случай, дано обобщение решений плоских задач механики трещин для упругопластического материала на случай пространственных проблем.
В [3] авторы отмечают, что многочисленные исследования показали существенное значение стесненной деформации в вершине трещины при изучении распространения трещины в рамках механики упругопластического разрушения и что влияние стесненности деформации (влияние геометрии нагружаемого образца и условий нагружения) подробно изучено в основном для задач чистого отрыва. Очень мало работ посвящено рассмотрению влияния стесненности деформации в вершине трещины на разрушение типа II или смешанного типа I/II в металлических материалах. Поэтому в [3] проведено численное исследование параметра стесненности деформации при сдвиговом нагружении для образца в условиях чистого сдвига. С помощью метода конечных элементов проведено моделирование образца, находящегося в условиях чистого сдвига, а также изучен диапазон допустимых значений параметра стесненности сдвиговой деформации.
В [4] получены оценки областей пластического течения вблизи краевых надрезов в условиях смешанного нагружения, полученные с помощью метода конечных элементов. Продемонстрирована геометрия пластических зон у вершины надрезов вдоль фронта трещины по толщине образца в трехмерной постановке упругопластической задачи.
В [5] в качестве основного метода исследования полей напряжений и перемещений у вершины трещины используются методы асимптотического анализа и синтеза, являющиеся классическими, стандартными методами анализа напряженно-деформированного состояния у вершины трещины, активно применяющимися в настоящее время для материалов с нелинейными определяющими уравнениями [7, 24–29].
В [6] представлен анализ процесса гибки металлического листа с возможностью образования трещин на поверхности. Для прогнозирования разрушения получено решение задачи гибки листа в условиях плоского деформированного состояния методом графического построения линий скольжения в идеально пластическом материале. В [7] приводится математическая постановка задачи о центральной трещине в пластине из упрочняющегося упругопластического материала в условиях плоского деформированного состояния. Получено численно-аналитическое решение задачи с использованием методов асимптотического анализа. В работе предлагается методика определения коэффициента нелинейности, характеризующего нелинейность диаграммы деформирования упругопластического материала.
В [8] дана экспериментальная оценка области пластического течения в условиях усталостного нагружения. Авторы [8] с помощью метода корреляции цифровых изображений и его комбинации с конечноэлементным анализом получили конфигурации области пластического течения у вершины усталостной трещины для различных режимов: от маломасштабного пластического течения до развитых пластических деформаций. Работа [9] также посвящена усталостному росту трещины, однако рассматривается смешанное нагружение и используется сканирующий электронный микроскоп для экспериментального определения направления роста трещины в условиях смешанного нагружения. В [10] обсуждаются экспериментальные методики определения зон пластического течения у вершины трещины.
В [11] авторы используют пластический коэффициент интенсивности напряжений для установления связи между двухосностью нагружения, свойствами материала и условиями пластического течения: от маломасштабного до развитого пластического течения в окрестности вершины трещины. Работа [12] посвящена теоретическому изучению параметров стесненности и их влияния на конфигурацию областей пластического течения у вершины трещины. В статье предложены новые параметры, эффективно описывающие пластические зоны у вершин трещин нормального отрыва и поперечного сдвига. Показано, что эти параметры хорошо описывают пластическую зону как в условиях маломасштабного пластического течения, так и в условиях умеренного пластического течения.
Авторы статей [13, 14] с помощью методов асимптотического анализа построили поля напряжений у вершины трещины вблизи трещины в условиях смешанного нагружения и V-образного выреза для степенного закона Бейли – Нортона теории установившейся ползучести. В [13, 14] основным методом исследования является метод разложения по собственным функциям, приводящий к нелинейным задачам на собственные значения. В случае трещины и V-образного выреза в материале со степенным законом Бейли – Нортона теории установившейся ползучести в условиях смешанного нагружения нелинейные задачи на собственные значения решаются численно с помощью метода многопараметрической пристрелки, результаты которого требуют дополнительной проверки и обоснования. Хорошо известно, что в предельном случае, когда показатель нелинейности в степенных определяющих уравнениях увеличивается, поведение материала приближается к поведению идеально пластического материала. Поэтому представляется важным иметь аналитические выражения для компонент тензора напряжений в предельном случае идеально пластического материала в условиях смешанного нагружения, чему и посвящена настоящая работа.
Первыми работами, в которых были исследованы асимптотические механические поля вблизи вершины трещины в упрочняющемся по степенному закону материале при смешанном деформировании и получены аналитические представления для поля напряжений в окрестности вершины трещины в идеально пластическом материале в условиях смешанного нагружения, являются работы Ши [15, 16]. В [15] был впервые введен параметр смешанности нагружения, характеризующий вид смешанного нагружения,
Mp = 2arctg lim ^""(r"6 °7 , (1) П L r "Г' r б( r, 6 = °)J где ajj (r, 6) - компоненты тензора напряжений в полярной системе координат r, 6 с полюсом в вершине трещины.
Ши [16] впервые получил асимптотические поля напряжений у вершины трещины при смешанном нагружении и угловые распределения компонент тензора напряжений у вершины трещины в условиях смешанного нагружения для степенного закона упрочнения для плоского деформированного состояния и рассмотрел предельный случай идеально пластического материала, для которого приведены аналитические выражения поля напряжений для четырех значений параметра смешанности нагружения Мр = °,°; 54,0; 84,1. Таким образом, в работе [16] рассмотрены два значения параметра смешанности нагружения, соответствующие чистому поперечному сдвигу и чистому нормальному отрыву, и два значения параметра смешанности нагружения, отвечающие непосредственно смешанному нагружению.
Для значения показателя упрочнения n = 13 приведено сравнение угловых распределений компонент тензора напряжений, построенных численно, с аналитическим решением, найденным для идеально пластического материала. Сравнение показывает их хорошее совпадение. Дальнейшее изучение поля напряжений у вершины трещины в идеально пластическом теле шло по двум направлениям: 1) построение поля напряжений для всего диапазона значений параметра смешанности нагружений и 2) устранение скачка радиальной компоненты тензора напряжений и построение непрерывного поля напряжений в окрестности вершины трещины, что достигается за счет введения упругих секторов в окрестности вершины трещины. Так, одной из классических работ в построении асимптотических полей напряжений в окрестности вершины трещины в упругом идеально пластическом материале стало исследование [17], где построено асимптотическое решение статически определимой задачи для поля напряжений в окрестности вершины трещины в условиях смешанного нагружения в предположении реализации плоского деформированного состояния. Авторы показали, что асимптотическое решение хорошо согласуется с конечно-элементным решением для целого ряда значений параметра смешанности нагружения. В работе [17] подробно рассмотрены четыре значения параметра смешанности нагружения Мр = 0,16; 0,54; 0,7; 0,84 для нагрузок, при которых область пластического течения охватывает не всю окрестность вершины трещины и имеются упругие секторы в окрестности вершины трещины. С помощью двух допущений: 1) об ограниченности поля напряжений и 2) о непрерывности всех компонент тензора напряжений – авторам удалось построить асимптотическое решение задачи для трех указанных значений параметра смешанности нагружения. Несмотря на приведенный детальный анализ секторов, формирующих поле напряжений, в статье [17] не получено решение для всех значений параметра смешанности нагружения. Кроме того, при более высоких нагрузках пластическая область может охватывать всю окрестность вершины трещины (без упругих секторов) [18], а для таких смешанных нагружений асимптотические решения, по всей видимости, отсутствуют.
Проблема построения аналитических решений для поля напряжений вызывает интерес и в настоящее время [2, 12, 14, 17]. Так, в [19] проанализированы асимптотические поля напряжений у вершины стационарной трещины отрыва в условиях плоского деформированного состояния в несжимаемом материале. Предложено 5-секторное решение, включающее в себя в качестве частных случаев решения, полученные в [20, 21].
К построению поля напряжений у вершины трещины в упругом идеально пластическом материале при смешанном нагружении в условиях плоского напряженного состояния позже обращались и другие исследователи [22]. В [22] построено непрерывное поле на- пряжений в окрестности вершины трещины в условиях плоского напряженного состояния с использованием упругих секторов вблизи вершины трещины. Таким образом, можно заключить, что свойственное отсутствие непрерывности радиального напряжения в решении для идеально пластического материала снимается путем введения упругих зон в окрестности вершины трещины. Тем не менее решение для идеально пластического материала представляет собой предельное решение для полей напряжений Хатчинсона – Райса – Розенгрена [23–25] в окрестности вершины трещины в упрочняющемся по степенному закону материале. При построении угловых распределений компонент тензора напряжений в упрочняющихся по степенному закону материалах и в материалах, следующих степенному закону ползучести Бейли – Нортона, очень важным оказывается знание закономерностей угловых распределений компонент тензора напряжений для смешанного деформирования [14, 26–32]. Мотивом настоящего исследования послужило отсутствие аналитических представлений для компонент тензора напряжений в окрестности вершины трещины в идеально пластическом материале в полном диапазоне смешанных форм нагружения от чистого поперечного сдвига до чистого нормального отрыва и анализ угловых распределений напряжений для различных значений параметра смешанности нагружения. Поэтому целью настоящей работы является асимптотический анализ поля напряжений в окрестности вершины трещины в идеально пластическом материале в условиях смешанного нагружения в предположении реализации плоского напряженного и плоского деформированного состояния без предположения существования упругих зон в окрестности вершины.
1. Математическая постановка задачи и основные уравнения
Определение напряженного состояния в окрестности вершины трещины в идеально пластическом материале приводит к необходимости решения следующей системы уравнений:
– уравнений равновесия
^ rr + 1 8° r9 + ° rr -Ggg = 0
5 r r 99 r ’
d° r 0 + 1 d°99 , 2° r 9 = 0
d r r d9 r ,
– условия пластического течения
( ° rr — ° 99 ) 2 + 4 0 2 9 = 4 k 2 ,
О2T - °rr°99 +О29 + 3°29 = 3k2, где k = °Y / V3, °Y - предел текучести при растяжении для плоского деформированного и плоского напряженного состояния соответственно.
Граничные условия задачи есть условия отсутствия поверхностных усилий на берегах трещины
-
□ ее ( г , е = ± п ) = 0, □ r е ( г , е = ± п ) = 0. (4)
-
2. Асимптотическое решение задачи.
Вид смешанного нагружения характеризуется значением параметра смешанности нагружения M p (1). Заданное значение параметра смешанности нагружения замыкает математическую постановку задачи.
Плоское деформированное состояние
Распределение напряжений в окреcтности вершины трещины можно получить следующим образом. Опираясь на асимптотический анализ уравнений равновесия, проведенный в [33] и дополнительно представленный в [17], можно разыскивать напряжения в непосредственной окрестности вершины трещины в виде разложения по собственным функциям
-
□ у( г ,е ) = о 00) ( е ) + r □0° ( 0 ) , г ^0. (5)
В дополнение можно отметить, что в случае плоского деформированного состояния справедливо равенство е 33 = 0. Исходя из этого равенства, как по уравнениям теории течения, так и по уравнениям деформационной теории, справедливо соотношение □ = ( □„ + а 22 ) / 2 . Поэтому напряжения в окрестности вершины трещины ограничены и их можно искать в асимптотической форме (5). Подставляя асимптотическое разложение (5) в разрешающую систему уравнений (2), (3) и пренебрегая малыми при г ^ 0 величинами, приходим к системе обыкновенных дифференциальных уравнений
(0) (0) (0) (0)(0)
-
□ ге,е + □ гг - □ее = 0, □ее,е + 20ге = 0
и алгебраическому условию пластического течения
(0) (0) 2(0) 22
(□ гг □ее ) + 4(□ ге ) 4k .
Условие пластического течения (7) будет тождественно выполнено, если положить
□ гг ) □ ( е ) - k cos2 0 (0)( 0 ),
-
□ ее) = □(0) (е)+k cos 2©(0) (е),(8)
□(г0) = к sin20(0)(0), где □(0) (е),0(0)(е) - функции, подлежащие определению в ходе решения задачи.
Исследование системы уравнений (6), (7) вместе с граничными условиями на берегах трещины (4) приводит к хорошо известным распределениям для трещин нормального отрыва [34–37], состоящим из пяти секторов:
-п < е < - 3 п / 4,
-
□ 00) = — + — cos20, □ 00) = — - — cos20, □ (0) =- — 8ш20,
I гг 2 2 ” 2 2 г " 2
- 3 п / 4 < е < -п / 4,
‘ (0) - Гт(0) - А — 3 п (0) - — □ гг =^ ее =е + 2 + -4, □ г е = - 2,
-п / 4 < е < п / 4,
-
□г0, = —+ —- — cos20, а(0, = —+ —+—cos20, ст00, = — sin2е, [ гг 2 2 2 2 2 2
п / 4 < е < 3 п / 4,
‘ Гт(0) - Гт(0) - А — 3п Гт(0)-
-
□ гг = □(* =-е + 2 + "4", □ ге
- 3 п / 4 < е < п ,
-
□ 00) = — + — cos20, □00) = — - — cos20, □00) =- — sin2е, гг 2 2 ^ 2 2
и поперечного сдвига, состоящим из семи секторов:
-п = е , < е < е 2 = - 3 п / 4,
-
□ 00) = — + — cos20, □ 00) = — - — cos20, □ 00) =- — sin2 е , гг 2 2 ^ 2 2 г " 2
е 2 <е<е 3 =- (5 п / 8 +и 4,,
-
□ г =□ ее ) =е+ — / 2 + 3 п / 4, □ г °в) =- 1 / 2,
е 3 <е<е 4 = е 3 + п / 2,
-
□ г 0, =е 3 + 2 + 3 п- 2cos2 ( е-е 3 + 3 п / 4 ) ,
-
□ ее ) = е 3 + 2 + 3 ^+ 2cos2 ( е-е 3 + 3 п / 4 ) ,
-
□ г 0) = - 2 sin 2 ( е-е 3 + 3 п / 4 ) ,
J е4<е<е5 =п/8+1/4, | ,—(0) _ ,—(0) _ _А гг(0) — 1 Л [□ гг □ее е, □ ге 1'2, е5 <е<е6 = 5п/8+1/4,
-
□ 00) = - — -—- — cos2 ( е-е5 -п / 4 ) ,
гг 4 8 2 V 5 7
-
□ ее ) =- 4 -1- 2COS2 ( е-е 5 -п / 4 ) ,
-
□ г е ) =- 2sin2 ( е-е 5 -п / 4 ) ,
J е 6 < е < е 7 = 3 п / 4,
[□г0)=□ее)=е -—/2 - 3п/4, □ге)=-—/2, е 7 < е < п,
-
□ 00) =- — - — cos 2 е , □ 00) =- — + — cos 2 е , □ 00) = — sin2 е .
гг 2 2 ” 2 2 г е 2
В соотношениях (9) и (10) все компоненты тензора напряжений отнесены к пределу текучести при чистом сдвиге k и записаны в безразмерной форме. Пользуясь распределением напряжений (10), справедливым для трещины поперечного сдвига в идеально пластическом материале, можно построить решение для произвольно- го значения параметра смешанности нагружения M p (1). Обобщение формул (10) на случай смешанного нагружения включает семь секторов и имеет вид:
Формулируя условия непрерывности компонент о'0) (9) и о(0) (9) на луче 9 = 9,, можно получить вы-99 r9 6
ражения для углов 9 5 , 9 6 :
-п = 91 < 9 < 92 = -3п/4, ^r = (1/2) + (1/2)cos29, ^ = (1/2) — (1/2)cos29, о09) = -(1/2)sin29,
-
1 < I п Я Л и I 1 п А 1 < I п Я Л и I 1 5п/1 \
-
9, = -tg —Mp + - + —, 9, = -tg —Mp + - +—.(13)
5 4 Ч2 J 4 8, 6 4 Ч2 J 4 8
J 9 2 <9<9 3 ,
К) = о 99 ) = 9 + 1 / 2 + 3 п / 4, о 9 9 ) = - 1 / 2,
9 з <9<9 4 ,
о (9) = 93 +1 + — - 1cos2 ( 9-9 + 3п / 4 ) , 99 3 2 4 2 7
о99) = 9з + 2+3П+-^cos2 (9-9з+3п/4), о9 9) =- 2sin2 (9-93 + 3п/4),
J9 4 < 9 < 9 5 о 0 ") = о 99 ) = -9 + (1 / 2)tg(n M p 1 2), (1
М9 ) = 1 / 2,
9 5 < 9 < 9 б о^ = -9 5 + (1 / 2)tg( n M p / 2) +
+ (1 / 2)cos2 ( 9-9 5 -п / 4 ) ,
< о99) = -95 + (1/2)tg(nMp/2) - (1/2)cos2(9-95 -п/4), о99) = -(1/2) sin 2 (9-95 -п/4),
Из соотношений (13) следует, что при Mp = 0,3301952 угол 9 6 становится равным 3п/4 и область 9 6 < 9 < 9 7 исчезает из решения. Следовательно, распределение (11) справедливо для всех значений параметра смешанности нагружения из диапазона 0 < Mp < 0,3301952. При значениях параметра смешанности нагружения, превышающих M p = 0, 3301952,
асимптотическое решение задачи определяется соотношениями, образующими шесть секторов:
-п = 9 1 < 9 < 9 2 = -3п / 4,
о '") =1 +1 cos 29, о '0) =1 -1 cos 29, о '") =-1 sin 29, 99 2 2 2 2 9 2
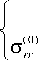
9 2 <9<9 3 ,
= о 99) =9 + 1 / 2 + 3 п / 4, 99
о 9 9 ) =- 1 / 2,
J9 6 < 9 < 9 7 = 3п / 4 о Г0 = о 99 ) = 9 -1 / 2 - 3п / 4, [о 0 9 ) =-1 / 2,
9<в<” ,
= - (1 / 2) - (1 / 2) cos 2 9 , ^ = - (1 / 2) + (1 / 2) cos 2 9 , о 0 9 ) = (1 / 2) sin 29.
В выражения (11) входит параметр смешанности нагружения: на отрезке 9 4 < 9 < 9 5 компоненты тензора напряжений определяются соотношениями, найденными с помощью определения параметра смешанности нагружения (1) и общей структуры решения задачи (8): о^ =о 99 ) =-9 + (1 / 2)tg(п M p / 2), что позволяет получить решения для различных значений M p . Неизвестные углы 9 3 , 9 4 , 9 5 , 9 6 определяются из условий непрерывности компонент тензора напряжений о 99 ) ( 9 ) и о 9 9 ) ( 9 ) на лучах, разделяющих сектора. Формулируя условия непрерывности на лучах 9 = 9 4 , можно получить выражения для углов 9 3 , 9 4 :
93 <9<94, о'") =93+1 + — - 1cos2 (9-93+ 3п/4), 99 3 2 4 2 v 3 7
о'9) =93 + 2 + 3- + 2cos2 (9-93 + 3п/4), о99) = - ^sin2 (9-93+3п/4),
94 <9<95, о90) = о'") = -9 + (1/ 2)tg(пMp / 2), о0") = 1/2,
95 <9<9б, о90) = -95 + (1/2)tg(пMp /2) + (1/2) cos 2 (9-95 - п/4), < о'0") =-95 + (1/2)tg(пMp /2) - (1/2)cos2 (9-95 -п/4), о99) =-(1/2)sin2 (9-95-п/4),
9 б <9<п ^ = - 2 - 2 cos2 9 , о ' 0 ) = - 1 + 1 cos 2 9 , о '") = 1 sin 2 9.
99 2 2 9 9 2
Углы 9 3 , 9 4 вычисляются с помощью формул (12), поскольку в области -п < 9 < 0 решение сохраняет свою структуру, а углы 9 5 , 9 6 находятся из уравнений
1 Л ТЕ А
93= -tg I- M p I-
3 4 1 2 J
5 п a 1 . I п 1 D
--, 94 = -tg — M p
8 4 4 9 2
-
- ?(12)
1 Г
-9, + -tg I п M p I
5 2 ( 2 J
- 2 cos2 1 9 6
- sin2 1 9 6 -9 5
-
-9 5
п
-
---1—cos 29,,
22 6
п
= sin2 9 6 .
Результаты решения задачи представлены на рис. 1–3, на которых приведены угловые распределения компонент тензора напряжений, определяемые соотношениями (11) и (14).
лиз решения (14) при увеличении параметра смешанности наружения показал, что угловые распределения компонент тензора напряжений выходят на решение, отвечающее нормальному отрыву при Mp = 0,8896724.
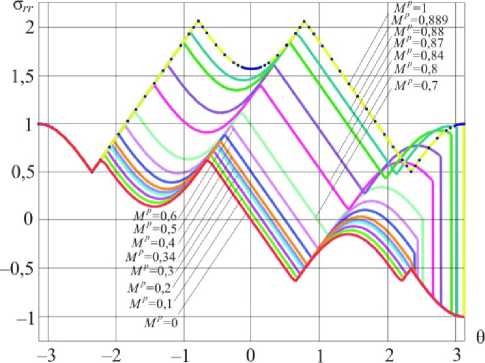
Рис. 1. Распределения радиального напряжения ст ( г 0) в окрестности вершины трещины для различных значений параметра смешанности нагружения (плоское деформированное состояние)
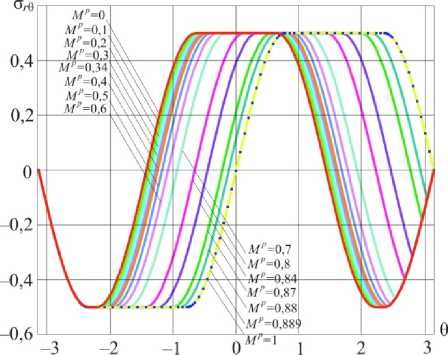
Рис. 3. Распределения касательного напряжения CT r U ) в окрестности вершины трещины для различных значений параметра мешанности нагружения (плоское деформированное состояние)
Fig. 1. Distributions of the radial stress ст^ ) in the vicinity of the crack tip for different values of the mixity parameter (plane strain condition)
Fig. 3. Distributions of the shear stress о Г U ) in the vicinity of the crack tip for different values of the mixity parameter (plane strain condition)
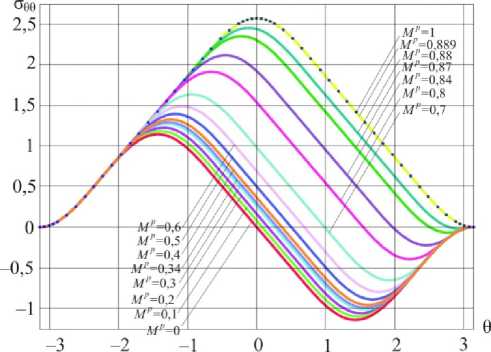
Рис. 2. Распределения тангенциального напряжения в окрестности вершины трещины для различных значений параметра смешанности нагружения (плоское деформированное состояние)
Для всех значений параметра смешанности нагружения из отрезка 0.8896724 < Mp < 1 решение описывается формулами (9), отвечающими чистому нормальному отрыву (см. рис. 1–3) (решение включает пять секторов). На рис. 1–3 можно ясно видеть переход от чистого поперечного сдвига к чистому нормальному отрыву. Кривая красного цвета на каждом из рисунков показывает распределение компонент тензора напряжений для чистого поперечного сдвига (первый предельный случай Mp = 0): компоненты тензора напряжений ст ( г 0) , o UU ) являются антисимметричными относительно оси ординат, тогда как касательное напряжение ст ( г U ) симметрично . Кривые, изображенные синими точками, отвечают второму предельному случаю – чистому нормальному отрыву ( Mp = 1). Здесь, напротив, компоненты ст^, ct UU симметричны относительно оси ординат, а касательное напряжение ст^ ) - антисимметрично.
Fig. 2. Distributions of the circumferential stress ст^0,) in the uu vicinity of the crack tip for different values of the mixity parameter (plane strain condition)
Следует отметить, что при значениях параметра смешанности нагружения, близких к единице (при нагружениях, близких к нормальному отрыву), решение обладает особенностью. Можно было бы ожидать, что при стремлении параметра смешанности к единице распределение (14) будет непрерывным образом стремиться к решению (9). Однако не существует конечного предела функций, которыми задается решение, в областях U 4 < U < U 5 и U 5 < U < U 6 при Mp ^ 1. Ана-
-
3. Асимптотическое решение задачи.Плоское напряженное состояние
В случае плоского напряженного состояния асимптотическое решение задачи будем также искать в форме (5). Справедливы уравнения равновесия (6), но условие пластического течения имеет вид
(0) 2(0) (0) (0) 2(0) 22
( CT rr ) CT rr CT UU + ( CT UU ) + 3 ( CT r U ) = 3 k . (15)
Условию пластического течения для плоского напряженного состояния (15) можно тождественно удовлетворить, если положить [37, 38]
ст ? = k cos 6, O gg ) = 2 k cos 6, o ? 0) = k sin 6. (16)
Известно и иное распределение компонент тензора напряжений, приводящее к тождественному выполнению условия пластического течения [30, 38]:
a00 = a + b cos20(6) + c sin20(6), o0o0) = a -bcos20(6)-csin20(6), (17)
Or0) =- b sin20(6) + c cos20(6), где a,b,c – такие постоянные, что a2 + 3 b2 + 3 c2 = 3 k2. (18)
Хорошо известны решения для задач о трещинах нормального отрыва [30, 38, 39] (здесь и далее напряжения отнесены к пределу текучести k ):
I 0 £0£в | ,
-
-. = 2 o = -^cos 6 , o ?0 = -^sin 6 ,
6 ’ <6<6 2 ,
o (,0) = ’ ( - 1 + 3cos262 ) + ’ ( 1 + cos262 ) x
4 4
x cos 2 ( 6-6 2 ) + ’sin2 6 2 sin 2 ( 6-6 2 ) ,
-
• 0 66 ) = 4 ( - 1 + 3cos2 6 2 ) - 4 ( 1 + cos2 6 2 ) x (19)
x cos 2 (0-02)-’sin262 sin 2 (6-62), o?6) =- 4 (1 + cos 262) sin2 (6-62) +
+ 2 sin 2 6 2 cos2 ( 6-6 2 ) ,
62 < 6 < П, o'.0' =-1 -1 cos 26, o00) =-1 +’cos 26, o^) =1 sin 26, rr 2 2 2 2 6 2
где углы 6, = 1,39233 = 79,77°, 62 = 2,63960 = 151,24° определяются из решения системы трансцендентных уравнений
6 1 <6<6 2 ,
C = 2 o’ = ^=cos ( 6 + c 3 ) , o ■ 6 = ^3 sin ( 6 + c 3 ) ,
6 2 <6<6 3 ,
S^ = "2"cos ( 6 2 + с 3 ) - 2/3cos ( 6 2 + с 3 ) x x cos 2 ( 6-6 2 ) + -’3 sin ( 6 2 + с 3 ) sin 2 ( 6-6 2 ) , 31
O 99 = —cos ( 6 2 + с 3 ) + 223cos ( 6 2 + с 3 ) x (20)
x cos 2 (6-62)- -’= sin (62 + с3) sin 2 (6-62), o?6) = -2’=cos (62 + с3) sin2 (6-62) + + -13 sin (62 + с3) cos 2 (6-62),
6 3 <6<6 4 ,
O 00) = 2 o (0 = - ^3 sin 6 , O ? в = ^ cos 6 ,
6 4 <6<6 5 ,
O’ = "2"cos ( 6 5 + с 2 ) - 2y3cos ( 6 5 + с 2 ) x x cos 2 ( 6-6 5 ) + -’3 sin ( 6 5 + с 2 ) sin 2 ( 6-6 5 ) ,
O 0 9 ) = —cos ( 6 5 + с 2 ) + ^^cos ( 6 5 + с 2 ) x x cos 2 ( 6-6 5 ) - ^3sin ( 6 5 + с 2 ) sin 2 ( 6-6 5 ) ,
O ? 0 ) = 213 cos ( 6 5 + с 2 ) sin 2 ( 6 - 6 5 ) +
+ 73sin ( 6 5 + с 2 ) cos2 ( 6-6 5 ) ,
—’ sin 6, =- — (1 + cos26,)x V3 ’4 ( 2 )
x sin2 ( 6 1 -6 2 ) + ’sin2 6 2 cos2 ( 6 1 -6 2 ) ,
—cos 6. = —( - 1 + 3cos26, ) -
V3 ’ 4 ( 2 )
- 4 (1 + cos 262) cos2 (61 -62)-’sin262 sin2 (61 -62), и поперечного сдвига [36] в идеально пластическом материале
-n < 6 < 6 ’ ,
0 (0) =1 + ’cos 26, o0 0) =1 - ’cos 26, 0 (0) =- ’sin 26,
[ rr 2 2 2 2 6 2
6 5 <6<6 б ,
C = 2000 = ^23 cos ( 6 + c 2 ) , 0O0 ) = ^3 sin ( 6 + c 2 ) ,
6
б
<6
O 00) =-1 - ’cos 26, o^ ) =-1 + ’cos 26, O 00) = ’sin 26. rr 2 2 66 2 2 r 6 2
В асимптотическом решении (20) углы 6 1 , 6 2, 6 3, 6 4, 6 5, 6 6 и константы с 2, с 3 определяются из условий непрерывности тангенциального и касательного напряжений на лучах, разделяющих сектора, – условий, приводящих к необходимости решения следующих систем уравнений. Угол 6 6 и константа с 2 находятся из системы уравнений
Угол нений
Углы нений
^3 cos ( 9 6 . c 2 ) = - - ( 1 - Cos 2 9 6 ) , ^sin ( 9 6 . c 2 ) = jsin ( 2 9 6 ) .
9 1 и константа с3 находятся из системы урав-
-y= cos ( 9 1 + c 3 ) = 2 ( 1 - cos 2 9 1 ) , - Tssin ( 9 i + c 3 ) = Is™ ( 2 9 i ) .
9 2 , 9 3 вычисляются с помощью системы урав-
- ^=sin 9 3 = —cos ( 9 2 + c 3 ) +
+— ^=cos ( 92 + c ) cos2 ( 93
- ^=sin ( 9 2 + c 3 ) sin 2 ( 9 3
9 2 )
9 2 ) ,
-Ucos93 = —^cos ( 92 + c 3) sin2 ( 93 - 92 ) + 323
+ "2= sin ( 9 2 + c 3 ) cos 2 ( 9 3 - 9 2 ) .
Углы 9 4 , 9 5 вычисляются с помощью системы уравнений
- V3 sin 9 4 = "2"COs ( 9 5 + c 2 ) +
.—^ cos (95 + c 2) cos 2 (94
- ^3sin ( 9 5 + c 2 ) sin 2 ( 9 4
9 5 )
-9 5 ) ,
—i= cos 94 = —cos ( 95 + c 2) sin2 ( 94 323
-9 5 ) +
+ ^3sin ( 9 5 + c 2 ) cos 2 ( 9 4
-9 5 ) .
Обобщение представления (20) на случай смешанного нагружения позволяет получить асимптотическое решение для значений параметра смешанности нагружения, близких к поперечному сдвигу. Анализ соотношений (20) указывает на их справедливость для смешанного нагружения с заменой решения в секторе 9 3 < 9 < 9 4 на выражения
9 3 < 9 < 9 4
o« = X’ = ^3cos ( 9 + с 1 ) , c r 9 = ^3sin ( 9 + c i ) ,
где константа определяется из соотношения (1) и
। 1 |Пввп]| с. = arcctg — tg — M
1 I 2 ( 2 J J
отражает вид смешанного нагружения. Аналитическое решение (20) для других секторов сохраняется и для смешанного нагружения. Таким образом, для смешанного нагружения поле напряжений определяется различными зависимостями в семи секторах:
-n < 9 < 9 1
(0) 1 1 (0) 1 1 (0) 1
X = 2 + 2cos2 9 , X’ = 2-2cos2 9 ,< 9 ’ —2sm2 9 ,
9 1 <9<9 2
O« = 2 ^ 0 0’ = ^23 cos ( 9 + c 3 ) , ^ 9 = ^sin ( 9 + c 3 ) ,
9 2 < 9 < 9 3
^ rr ’ = ^"cos ( 9 2 + с 3 ) - 2/3 cos ( 9 2 + с 3 ) x
x cos 2 ( 9-9 2 ) + ^3sin ( 9 2 + с 3 ) sin 2 ( 9-9 2 ) ,
r
CT 9e ) = -ycos ( 9 2 + с 3 ) + — 3 c os ( 9 2 + с 3 ) x < 26 ’
x cos 2 ( 9-92 ) - ^=sin (92 + c 3) sin 2 ( 9-92 ) ,
,.21,.:. . »»-..
+ 23sin ( 9 2 + с 3 ) cos2 ( 9-9 2 ) ,
9 3 <9<9 4
= 2 ^ r 0’ = .( 9+ с ) , ^ Г 9 = ^3sin ( 9+ с ) ,
9 4 <9<9 5
G<9’ = cos (9, + с, )--;=cos (9, + с2 )x rr 2 52 23 52
x cos 2 ( 9-9 5 ) + ^3sin ( 9 5 + с 2 ) sin 2 ( 9-9 5 ) ,
r C = 2fcos ( 9 5 + с 2 ) + 213 cos ( 9 5 + с 2 ) x
x cos 2 ( 9-9 5 ) - ^sin ( 9 5 + с 2 ) sin 2 ( 9-9 5 ) ,
^ r 9 ’ = 2^cos ( 9 5 + с 2 ) sin2 ( 9-9 5 ) +
+ ^3sin (95 + с2) cos2 (9-95), r 2 °, <«<«. 1
^a = X0’ = 23cos ( 9+ c 2 ) , ° r 9 ’ = 23sin ( 9+ c 2 ) ,
9 6 < 9 < n
a (0’ =-1 -1 cos 29, a (00’ =-1 +1 cos 29, a (°’ =1 sin 29.
rr 2 2 9 2 2 9 2
Появление в решении константы с 1 (переход к рассмотрению смешанного нагружения) приводит к изменению углов 9 2 , 9 3 , которые в случае смешанного нагружения определяются из системы уравнений
-4- cos ( 93 + c ) = —cos ( 92 + c 3) +
+— Lrcos ( 92 + c 3) cos2 ( 93 - 92 )
—L sin ( 92 + c 3) sin 2 ( 93 — 92 ) ,
-4. sin ( 9 3 + c 1 ) = 2~3 cos ( 9 2 + c 3 ) x
x sin 2 ( 9 3 — 9 2 ) + -4 sin ( 9 2 + c 3 ) cos 2 ( 9 3 — 9 2 ) .
Углы 9 4 , 9 5 в случае смешанного нагружения вычисляются с помощью системы уравнений
^ cos ( 9 4 + c ) = — cos ( 9 5 + С 2 ) +
+— ^=cos (95 + c 2) cos2 (94
— 43 sin ( 9 5 + c 2 ) sin 2 ( 9 4
9 5 )
95 ) ,
92 <9<93,
C = 240) = "hcos (9+c1), 49 = ^3sin (9+c1), (29)
^3sin (94 + cl )= 2,3cos (95 + c2 )X x sin 2 ( 94 — 95) + ^3sin (95 + c 2) cos 2 ( 94 — 95).
При приближении значения параметра смешанности нагружения к Mp = 0,3918025 углы 9 2 , 9 3 приближаются друг к другу и совпадают для приведенного значения параметра смешанности нагружения, поэтому асимптотическое решение (26), состоящее из семи секторов, редуцируется к решению, состоящему из пяти секторов:
—л < 9 < 9,,
a (0) = —— — — cos29, a (0) = — — + — cos29, a (0) = —sin29,
I rr 2 2 9 2 2 9 2
93 <9<94,
g(0) =— (—1 + 3cos294) + —(1 + cos294)x
4 1 4
x cos 2 ( 9 — 9 4 ) + 2 sin 2 9 4 sin 2 ( 9 — 9 4 ) ,
1 1
< g(0) = -4(—1 + 3cos294) — 4(1 + cos294)xxcos2(9 — 94) — — sin294 sin2(9 — 64),
Gr0) =— 4 (1 + cos 294) sin2 (9 — 94) +
+ -2sin2 9 4 cos2 ( 9 — 9 4 ) ,
94 < 9 < n,
G 0, =—1 —1 cos 29, a (0) =—1 +1 cos 29, a ((0) =1 sin 29.
I rr 2 2 9 2 2 9 2
Значения углов 9 1 , 9 2 определяются из системы тригонометрических уравнений
— V3(1 — cos2 9 1 ) = 3cos ( 9 2 + c 1 ) +
+ cos ( 9 2 + c 1 ) cos 2 ( 9 1 —9 2 ) —
— 2sin ( 9 2 + c 1 ) sin2 ( 9 1 —9 2 ) , (30)
V3sin2 9 1 = cos ( 9 2 + c 1 ) sin2 ( 9 1 —9 2 ) +
+ sin ( 9 2 + c 1 ) cos2 ( 9 1 —9 2 ) .
Значения углов 9 3 , 9 4 определяются из системы тригонометрических уравнений
9 ,
<9<92,
ПГ = ^3cos (92 + с1 ) — ^cos (92 + с )x x cos 2 (9 — 92) + —4 sin (92 + с) sin 2 (9 — 92), ' 3 ' ' '
< g'01 = —4 cos(9, + с)+—^cos(9, + с)x 99 2Л ( 21) 2^ ( 2 1)
x cos 2 (9 — 92) — ^3sin (92 + с) sin 2 (9 — 92),
g(0) = —cos (92 + с) sin2 (9 —92) +
2^3 x x /
+ ^sm (92 + с) cos2 (9 — 92),
^3sin ( 9 3 + c 1 ) = — 4 ( 1 + cos 2 9 4 ) x x sin2 ( 9 3 —9 4 ) + -2sin2 9 4 cos2 ( 9 3 — 9 4 ) ,
-y= cos ( 9 3 + c 1 ) = 4 ( — 1 + 3cos2 9 4 ) —
— 4 ( 1 + cos2 9 4 ) cos2 ( 9 3 —9 4 ) — 4sin2 9 4 sin2 ( 9 3 — 9 4 ) .
Таким образом, два представления (26) и (29) полностью описывают поле напряжений в окрестности вершины трещины в идеально пластическом материале при условии, что пластическое течение охватывает вершину трещины. Представление (26) дает поле напряжений для значений параметра смешанности нагружения при значениях параметра смешанности нагружения, меньших Mp = 0,3918025. Параметры, входящие в зависимости (26), вычисляются с помощью уравнений (21), (22) и (27), (28). В случае смешанного нагружения,
отвечающего значениям параметра смешанности нагружения, большим M p = 0,3918025, решение описывается формулами (29), в которых значения углов вычисляются из уравнений (30) и (31). Результаты вычислений показаны на рис. 4–6, где приведены угловые распределения компонент тензора напряжений для всех значений параметра смешанности нагружения (в полном диапазоне смешанных форм деформирования от чистого поперечного сдвига до чистого нормального отрыва, когда параметр смешанности нагружения пробегает значения от нуля до единицы).
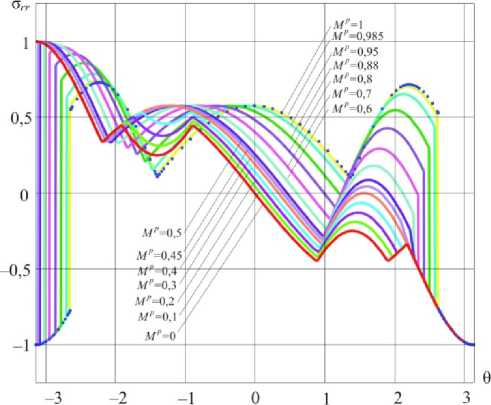
Рис. 4. Распределения радиального напряжения в окрестности вершины трещины для различных значений параметра смешанности нагружения (плоское напряженное состояние)
Fig. 4. Distributions of the radial stress σ ( rr 0) in the vicinity of the crack tip for different values of the mixity parameter (plane stress condition)
Следует отметить, что в случае плоского напряженного состояния константа с 1 , связанная с параметром смешанности нагружения уравнением (25), принимает значения π / 2 для поперечного сдвига и нуль – для нормального отрыва. При стремлении константы с 1 к нулю имеется конечный предел компонент тензора напряжений в уравнениях (29). Поэтому, как видно из рис. 4–6, увеличивая параметр смешанности нагружения до 1, можно получить распределение напряжений, соответствующее нормальному отрыву, в отличие от ранее рассмотренного случая плоского деформированного состояния.
Наглядную картину распределения радиального напряжения у вершины трещины при изменении параметра смешанности нагружения дают рис. 7–13, показывающие радиальное напряжение для трещины поперечного сдвига (рис. 7, а ), для смешанного нагружения (см. рис. 7–13) и для трещины нормального отрыва (рис. 13, б ).
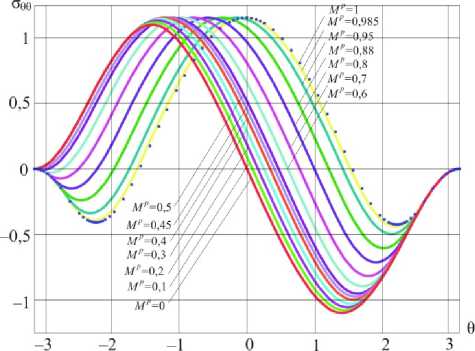
Риc. 5. Распределения тангенциального напряжения в окрестности вершины трещины для различных значений параметра смешанности нагружения (плоское напряженное состояние)
Fig. 5. Distributions of the circumferential stress σ ( θ 0 θ ) in the vicinity of the crack tip for different values of the mixity parameter (plane stress condition)
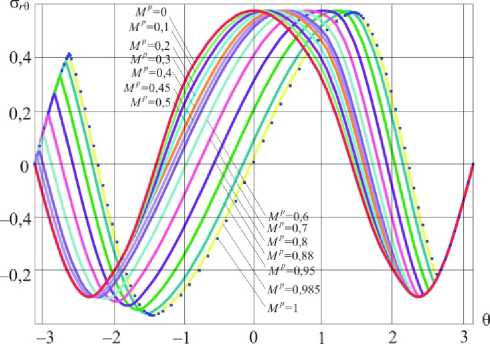
Рис . 6. Распределения касательного напряжения σ ( r 0 θ ) в окрестности вершины трещины для различных значений параметра смешанности нагружения (плоское напряженное состояние)
Fig. 6. Distributions of the shear stress σ ( r 0 θ ) in the vicinity of the crack tip for different values of the mixity parameter (plane stress condition)
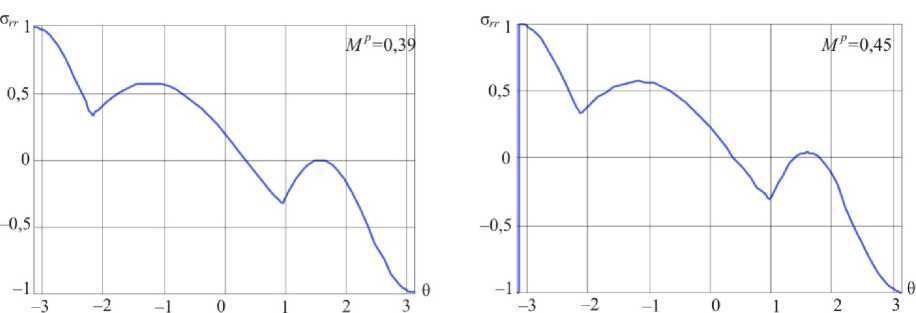
Из рис. 9 видно, что радиальное напряжение претерпевает резкие изменения вблизи θ =-π при переходе от значения параметра смешанности нагружения Mp = 0,39 к значению Mp = 0, 45, что может вызвать сложности при реализации метода двухпараметрической пристрелки для построения численных и асимптотических решений задач определения поля напряжений у вершины трещины в условиях смешанного нагружения в материалах, подчиняющихся степенному закону деформационной теории пластичности и степенному закону установившейся ползучести [38–44].
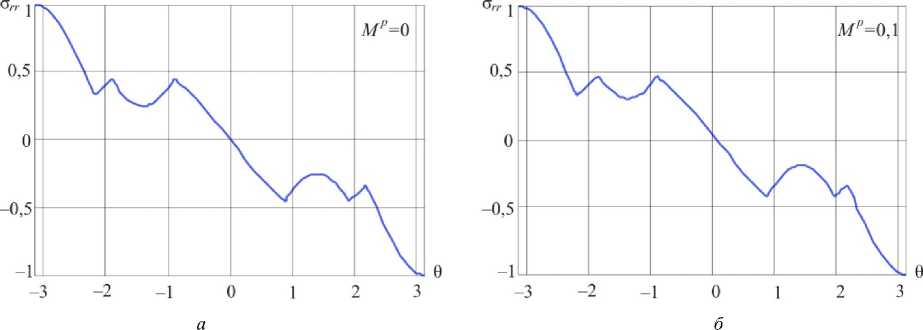
Рис. 7. Распределения радиального напряжения в окрестности вершины трещины поперечного сдвига
Mp = 0 ( а ) и для смешанного нагружения Мр = 0,1 ( б)
Fig. 7. Distributions of the shear stress a ™ in the vicinity of the crack tip for mode II crack ( а ) and for mixed mode crack M p = 0.1 ( b )
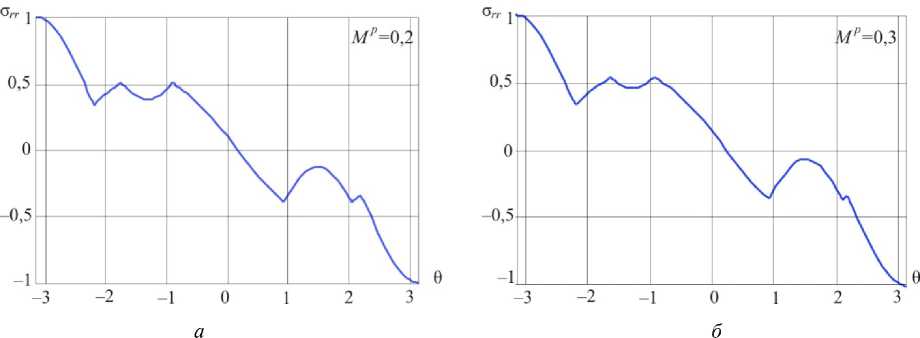
Рис. 8. Распределения радиального напряжения в окрестности вершины в условиях смешанного нагружения при Mp = 0,2 ( а ) и Mp = 0,3 ( б )
Fig. 8. Distributions of the shear stress a 0 0) in the vicinity of the crack tip for mixed mode crack M p = 0.2 ( а ) and M p = 0.3 ( b )
а б
Рис. 9. Распределения радиального напряжения в окрестности вершины в условиях смешанного нагружения при Mp = 0,39 ( a ) и Mp = 0,45 ( б )
Fig. 9. Distributions of the shear stress a 0 0) in the vicinity of the crack tip for mixed mode crack M p = 0.39 ( а )
and M p = 0.45 ( b )
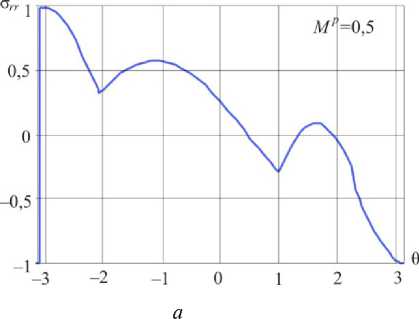
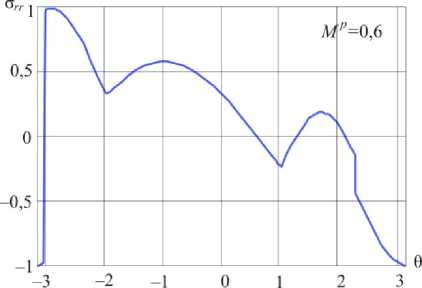
Рис. 10. Распределения радиального напряжения в окрестности вершины в условиях смешанного нагружения при Mp = 0,5 ( а ) и Mp = 0,6 ( б )
б
Fig. 10. Distributions of the shear stress a ™ in the vicinity of the crack tip for mixed mode crack Mp = 0.5 ( a ) and Mp = 0.6 ( b )
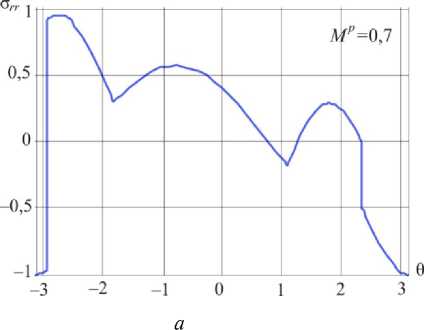
Рис. 11. Распределения радиального напряжения в окрестности вершины в условиях смешанного нагружения при Mp = 0,7 ( а ) и Mp = 0,8 ( б )
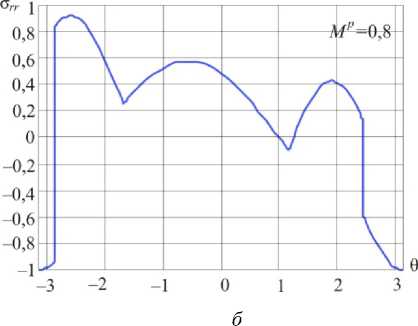
Fig. 11. Distributions of the shear stress О Т in the vicinity of the crack tip for mixed mode crack M p = 0.7 ( a ) and M p = 0.8 ( b )
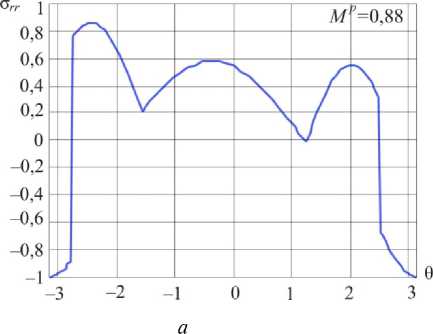
Рис. 12. Распределения радиального напряжения в окрестности вершины в условиях смешанного нагружения при Mp = 0,88 ( а ) и Mp = 0,95 ( б )
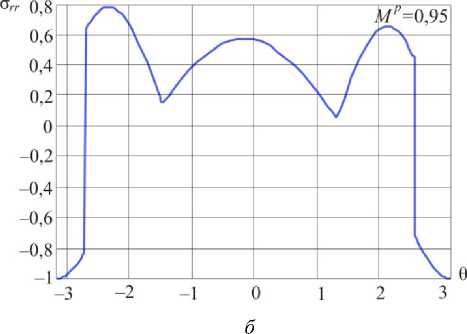
Fig. 12. Distributions of the shear stress a^ in the vicinity of the crack tip for mixed mode crack M p = 0.88 ( a ) and M p = 0.95 ( b )
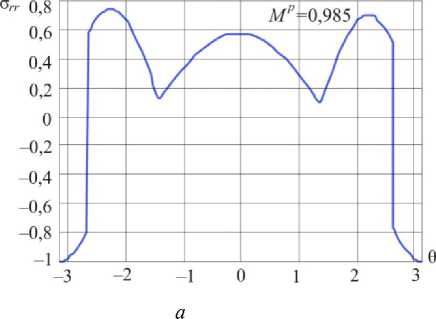
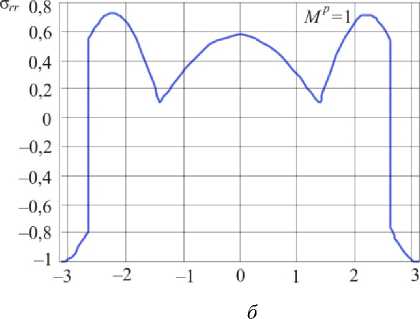
Рис. 13. Распределения радиального напряжения в окрестности вершины в условиях смешанного нагружения при M = 0,985 ( а ) и Mp = 1 ( б )
Fig. 13. Distributions of the shear stress a ™ in the vicinity of the crack tip for mixed mode crack M p = 0.985 ( a ) and Mp = 1 ( b )
Выводы и обсуждение результатов
В статье получены аналитические решения задач определения напряженного состояния у вершины трещины в идеально пластическом материале в условиях смешанного нагружения в предположении, что область пластического течения полностью охватывает вершину трещины для случаев плоского деформированного и плоского напряженного состояний.
Асимптотические решения получены для всего диапазона значений параметра смешанности нагружения, задающего вид деформирования. Полученные решения позволяют для указанного значения параметра смешанности нагружения построить угловые распределения компонент тензора напряжений.
Интересной и важной особенностью рассмотренного класса задач для плоского деформированного состояния является наличие отрезка значений параметра смешанности нагружения, для которого решение задается выражениями, не зависящими от параметра сме- шанности (справедливы единые зависимости (9) для всех значений параметра смешанности из отрезка 0,8896724 < Mp < 1). Для данного диапазона значений параметра смешанности нагружения трещина ведет себя как трещина отрыва, несмотря на наличие сдвиговой нагрузки.
Список литературы Асимптотические поля напряжений у вершины трещины в идеально пластическом материале в условиях смешанного нагружения
- Prandtl L. Ueber die Haerte plastischer Koerper. Goettinger Nachr, Math.-Phys. Kl. – 1920. – P. 74–85.
- Yusov F. Three-dimensional assessments of crack tip constraint // Theoretical and Applied Fracture Mechanics. – 2019. – Vol. 101. – P. 1–16.
- Ayatollahi M.R., Berto F. Развитие стесненной деформации в вершине трещины при упругопластическом разрушении в условиях сдвиговой нагрузки // Физическая механика. – 2018. – Т. 21, № 1. – C. 79–83.
- Turis M., Ivankova O. Using finite element analysis to obtain plastic zones in the vicinity of the crack edges, under mixed mode loading conditions // MATEC Web of Conferences. – 2020. – Vol. 310. – P. 00028.
- Karihaloo B.L., Xiao Q.Z. Асимптотические поля в вершине трещины в линейных и нелинейных материалах и их роль в распространении трещин // Физическая механика. – 2018. – Т. 21, № 6. – C. 23–35.
- Кожевникова Г.В. Решение задачи гибки листа методом полей линий скольжения // Известия Национальной академии наук Беларуси. Серия физико-технических наук. – 2018. – № 4. – С. 416–423.
- Гундина М.А. Метод асимптотичеcких разложений в задачах распространения трещин. Нахождение коэффициента нелинейности // Вестник МДУ имени А.А. Куляшова. – 2019. – № 1. – С. 63–70.
- Plastic zone evolution during fatigue crack growth: Digital image correlation coupled with finite elements method / J. Hozdez, M. Langlois, J.-F. Witz, N. Limodin, D. Najjar, E. Charkaluk, P. Osmond, A. Forre, F. Szmytka // International Journal of Solids and Structures. – 2019. – Vol. 171. – P. 92–102.
- Lesiuk G., Smolnicki M., Mech R., Ziety A., Fragassa C. Analysis of fatigue crack growth under mixed mode (I+II) loading conditions in rail steel using CTS specimen // Engineering Failure Analysis. – 2020. – Vol. 109. – P. 104354.
- Evaluation of the elasto-plastic crack tip singularities via mechano-luminescent effects / R. Basnet, S. Timisina, K.H. Le, J.S. Kim // International Journal of Engineering Science. – 2018. – Vol. 123. – P. 127–142.
- Couple effects of mixed mode biaxial loading and crack tip configuration on plastic stress intensity factor behavior at small and large scale yielding / A.P. Zakharov, V.N. Shlyannikov, A.M. Tartygasheva, D.V. Fedotova // Procedia Structural Integrity. – 2019. – Vol. 18. – P. 749–756.
- Huang X., Liu Y., Huang Z. New constraint parameters based on crack tip plastic zone: Theoretical derivations and effectiveness verification // International Journal of Solids and Structures. – 2020. – Vol. 190. – P. 129–147.
- A unified method to solve higher order asymptotic crack-tip fields of mode I, mode II and mixed mode I/II crack in power-law creeping solids / Y. Dai, Y. Liu, F. Qin, Y.J. Chao // Engineering fracture mechanics. – 2019. – Vol. 218. – P. 106610.
- Estimation of stress field for sharp V-notch in power-law creeping solids: An asymptotic viewpoint / Y. Dai, Y. Liu, F. Qin, Y.J. Chao, F. Berto // International Journal of Solids and Structures. – 2019. – Vol. 180–181. – P. 189–204.
- Shih C.F. Elastic-plastic analysis of combined mode crack problems. Ph. D. Thesis. Cambridge: Harvard University. 1973.
- Shih C.F. Small scale yielding analysis of mixed mode plane strain crack problems. In: Fracture Analysis, ASTM STP 560. 1974. American Society of Testing and Materials, Philadelphia. – P. 187–219.
- Dong P., Pan J. Plane – strain mixed-mode near-tip fields in elastic perfectly plastic solids under small-scale yielding conditions // International Journal of Fracture. – 1990. – Vol. 45. – P. 243–262.
- Zhu X.K., Chao Y.J. Fully plastic crack tip fields for CCP and DECP specimens under tension in non-hardening materials // International Journal of Solids and Structures. – 2000. – Vol. 37. – P. 577–598.
- Characterisation of crack tip stresses in elastic-perfectly plastic material under mode-I loading / I.A. Khan, V. Bhasin, J. Chattopadhyay, A.K. Glosh // International Journal of Mechanical Sciences. – 2011. – Vol. 53. – P. 207–216.
- Li J., Hancock J.W. Mode I and mixed mode fields with incomplete crack tip plasticity // International Journal of Solids and Structures. – 1999. – Vol. 36(5). – P. 711–725.
- Zhu X.K., Chao Y.J. Constraint effects on crack tip fields in elastic-perfectly plastic materials // Journal of the Mechanics and Physics of Solids. – 2001. – Vol. 49(8). – P. 363–399.
- Rahman M., Hancock J.W. Elastic perfectly plastic asymptotic mixed mode crack tip fields in plane stress // International Journal of Solids and Structures. – 2006. – Vol. 43. – P. 3692–3704.
- Hutchinson J.W. Singular behaviour at the end of a tensile crack in a hardening material // J. Mech. Phys. Solids. – 1968. – Vol.16. – P. 13–31.
- Rice J.R, Rosengren G.F. Plain strain deformation near a crack tip in a power-law hardening material // J. Mech. Phys. Solids. – 1968. – Vol. 16. – P. 1–12.
- Hutchinson J.W. Plastic stress and strain fields at a crack tip // J Mech Phys Solids. – 1968. – Vol. 16. – P. 337–347.
- Stepanova L.V. Intermediate self-similar asymptotic presentation of stress and damage fields in the vicinity of mixed mode crack tip under creep regime // Procedia Structural Integrity. – 2018. – Vol. 13. – P. 255–260.
- Larisa S., Ekaterina Y. Asymptotic stress field in the vicinity of the mixed-mode crack in damaged materials under creep conditions // Procedia Structural Integrity. – 2016. – Vol. 2. – P. 793–800.
- Stepanova L.V. Asymptotic stress field in the vicinity of a mixed-mode crack under plane stress conditions for a power-law hardening material // Journal of Mechanics of Materials and Structures. – 2015. – Vol. 10(3). – P. 367–393.
- Stepanova L.V., Yakovleva E. Stress-strain state near the crack tip under mixed-mode loading: Asymptotic approach and numerical solutions of nonlinear eigenvalue problems // AIP Conference Proceedings. – 2016. – Vol. 1785. – P. 030030.
- Астафьев В.И., Крутов А.Н. Распределение напряжений вблизи вершины наклонной трещины в нелинейной механике разрушения // Вестник Самарского университета. Естественнонаучная серия. – 1999. – № 4(14). – С. 56–69.
- Шлянников В.Н., Кислова С.Ю. Параметры смешанных форм деформирования для трещины // Известия Саратовского университета. – 2009. – Т. 9, № 1. – С. 77–84.
- Степанова Л.В., Яковлева Е.М. Смешанное деформирование пластины с трещиной в условиях плоского напряженного состояния // Вестник Пермского национального исследовательского политехнического университета. – 2014. – № 3. – C. 129–162.
- Rice J.R. A Path Independent Integral and the Approximate Analysis of Strain Concentration by Notches and Cracks // Journal of Applied Mechanics. –1968. – № 35(2). – P. 379–386.
- Качанов Л.М. Основы теории пластичности. – М.: Наука, 1969. – 420 с.
- Астафьев В.И., Радаев Ю.Н., Степанова Л.В. Нелинейная механика разрушения. – Самара: Самарский университет, 2001. – 632 с.
- Степанова Л.В. Математические методы механики разрушения. – М.: Физматлит, 2009. – 336 с.
- Milne I., Ritchi R.O., Karihaloo B.L. Comprehensive Structural Integrity. – Amsterdam: Elsevier, 2003. – 5232 p.
- Хилл Р. Математическая теория пластичности. – М.: Гостехиздат, 1956. – 408 с.
- Соколовский В.В. Теория пластичности. – М.: Высшая школа, 1969. – 608 с.
- Trapp M., Ochsner A. Computational Plasticity for Finite Elements: A Fortran – Based Introduction. Springer International Publishing, 2018. – 99 p.
- Saxena A. Advanced fracture mechanics and structural integrity. – Boca Raton: CRC Press, 2019. – 307 p.
- C(t) dominance of the mixed I/II creep crack. Part I. Transient creep / Y. Dai, Y. Liu, F. Qin, Y.J. Chao // Theoretical and Applied Fracture Mechanics. – 2019. – Vol. 103. – 102314.
- C(t) dominance of the mixed I/II creep crack. Part II. Extensive creep / Y. Dai, Y. Liu, F. Qin, Y.J. Chao, G. Qian // Theoretical and Applied Fracture Mechanics. – 2020. – Vol. 106. – P. 102489.
- Astafjev V.I., Stepanova L.V., Shesterikov S.A. Crack tip asymptotic character of anti-plane stress and strain rate for linear fractional constitutive relations // Theoretical and Applied Fracture Mechanics. – 1996. – Vol. 24, iss. 3. – P. 263–268.
- On the stress ahead of a stationary crack tip during the transition from primary to secondary creep / J.W. Sanders, M. Dadfarnia, H. Sehitoglu, J. Stubbins, P. Sofronis // International Journal of Solids and Structures. – 2020. – Vol. 193–194. – P. 455–473.
- Петухов Д.С., Келлер И.Э. Двойственные задачи плоских ползущих течений степенной несжимаемой среды // Вестник Самарского государственного технического университета. Серия: Физико-математические науки. – 2016. – Т. 20, № 3. – C. 496–507.
- Loghin A., Joseph P. Mixed mode fracture in power law hardening materials for plane stress // Journal of the Mechanics and Physics of Solids. – 2020. – Vol. 139. – P. 103890.


