Асимптотические решения уравнения Гельмгольца для псевдопериодических структур

В общем случае решение задач дифракции представляет собой сложную математическую задачу и требует специальных численных методов и значительных вычислительных затрат [1]-[6]. Асимптотические методы относятся к категории аналитических методов и играют большую роль [1]-[5]. В ряде случаев они позволяют быстро и эффективно оценить результат, не прибегая к громоздким численным расчётам. Для развития асимптотических подходов для решения уравнений Максвелла целесообразно рассмотреть более простую задачу решения уравнения Гельмгольца. Асимптотические методы решения уравнения Гельмгольца представлены в работе [4]. Приближение геометрической оптики, в рамках которого решается уравнение Гельмгольца справедливо только с случае, когда диэлектрическая проницаемость меняется медленно. Во многих случаях, например, дифракции света на дифракционной решетке, период которой составляет несколько длин волн, это условие не выполняется. Для решения задач дифракции в случае, когда объект представляет периодическую структуру, обычно используется дифференциальный метод [8]. Однако этот метод нельзя применить для решения задачи дифракции на непериодических структурах, например, бинарной линзе Френеля. Асимптотические методы решения уравнения Гельмгольца в случае, когда объект представляет собой структуру со слабоизменяющимся пространственным периодом, были рассмотрены в работе [7]. Однако метод решения, изложенный в статье, не давал результатов по сравнению с использованием приближения геометрической оптики при расчёте поля в плоскости непосредственно прилегающей к оптическому элементу. В данной работе метод был модернизирован, и на его основе получен асимптотический метод решения трехмерной задачи расчёта поля на выходе дифракционного оптического элемента.

1. Метод локальной аппроксимации

В данной работе предлагается метод, основанный на представлении объекта в окрестности точки x 0 псевдопериодической структуры дифракционной решеткой. Для расчета поля в окрестности произвольной точки x ₀ используется дифференциальный метод [8].

Рассмотрим дифракцию скалярного волнового поля на псевдопериодическом одномерном слое. В оптике этот случай описывает дифракцию волны, у которой вектор электрического поля лежит в плоскости

дифракционного оптического элемента (ДОЭ). ДОЭ предполагаем расположенным в области 0 ≤ z ≤ a , где 0 и a минимальная и максимальная высота дифракционного микрорельефа. Рассмотрим вычисление волнового поля в окрестности произвольной точки x 0 , расположенной на ДОЭ.

Волновое поле описывается уравнением Гельмгольца

д e  д e  2,; .

—у +--у + k sE — 0 , dx2   dzz

2™ где k — —— волновое число, л - длина волны.

В окрестности x ₀ распределение диэлектрической проницаемости описывается выражением

s ( x , z ) У s ” ( x o )exp

n

I n i” ( x - x ₀) d

где d – размер области, в которой производится аппроксимация.

Решение уравнения Гельмгольца в области ДОЭ, в области перед ДОЭ и в области за ДОЭ представим в виде

E ( x , z ) — exp ( ik a x ₀ ) ^ E ” ⁽ x o , ^{z )e}xp [ ^{ik a} ” ^{( x - x} o ) ] ⁽³⁾ n

E ( x , z ) —

— exp ( ik a x ₀ ) ^ I ” ( x ₀)exp [ ik a ” ( x - x ₀) + ik p n z ] + (4) n

+ exp ( ik a x ₀ ) ^ R ” ( x ₀) exp [ ik a n ( x - x ₀) - ik p n z ]

n

E ( x , z ) — exp ( ik a x ₀ ) x

^X Z T ” ( x 0 ) exp [ ik a ” ( x - x 0 ) + ikp_nz ] .

n

Коэффициенты I_n определяются падающим пучком. Коэффициенты R_n , T_n и функции E_n ( x, z ) подлежат определению: a m — a + 2 n im/kd , P m — V1 - a m² . Подставляя выражение (3) в (1) по-

лучаем систему обыкновенных дифференциальных уравнений для определения функций E n ( x, z ):

^{d 2} | m ( z ) + k ² ( s m - , - a X) E l ( z ) — 0. оz                      '

Решение системы дифференциальных уравнений и нахождение коэффициентов R_n , T_n рассмотрено в приложении 1. Поле в точке x ₀ непосредственно за оптическим элементом имеет вид:

E ( x , z ) = exp ( ik a x 0 ) S T n ( x ₀)exp [ ik p n a ] . (7) n

Волновое поле на некотором расстоянии за оптическим элементом можно вычислить с помощью интеграла Кирхгофа ([1]–[2]). Предлагаемый подход позволяет вычислить поле от оптического элемента с большой апертурой.

^ n = 7 S g m ⁽ x 0 ^)exp ( ikg ⁽ x 0 ⁾ )^x d_m

x exp - ik

(am - ton) 2 em

2. Дифракция на оптическом элементе, обладающем зонной структурой

Рассмотрим дифракцию на ДОЭ, обладающем зонной структурой. В случае дифракционного оптического элемента распределение диэлектрической проницаемости описывается выражением

J exp

-<

I n

e (x , z ) = S g n ( z )exP[ ikng ( x )],                (8)

n

где k g ( x ) – фазовая функция дифракционного оптического элемента. Границы зон определяются по формуле g ( x_m ) = m A .

В этом случае

^e n = £7 J g m ^{( x} 0 ⁺ ^ ^x m d - d/

x exp ( ikg ( x ₀ + £ ) m ) exp

Падающее поле имеет вид:

E ( x ) = K ( x ) exp ( ik ф ( x ) )

ik p m

ton - am pm

d ^ ,

_ K ( x 0 )exp ( ikф ( x 0 ) )

d

-

d

/2

И J exp ik — d/ 2

„f exp I -ikI x

(

- [ ^ - —I d ^ ,

dg      d2 g     дф      d 2ф где a = ^ , в = 7Г, Y = —, И = дx 0       дx 0       дx 0       дx 0

ложить

.

dg и в = 0 приближенно можно по-dx 0

^£ m = g m ⁽ x 0 ^)exp ( ikg ⁽ x 0 ⁾ m ) ,                  ⁽¹⁶⁾

I n = exp ( - ik a x 0 ) K ( x 0 )exp ( ik ф ( x 0 ) ) 0 “,     (17)

I_n = 7 J K ( x о + ^ )exp ( ik( Ф ( x о + £ ) - 0^ ) ) x d - d/

x exp

дФ где о = —, K (x) - амплитуда падающей ax о

волны,

ϕ ( x ) - эйконал падающей волны.

В случае, когда функция g ( x ) плавно изменяется, выражение для коэффициентов Фурье имеет вид:

^e n = ^7 J g m ⁽ x 0 ^)exp ( ikg ⁽ x 0 ) m ) m d - d/

2nn где ®n    i , kd d2

In = ^( x ^ J exp ( ^ik( Ф ^{( x} 0 ⁾ )^{x d} -/

x exp f ik ^И ^ j exp ( - i to n ^ ) d ^ .

После элементарных преобразований выражение для коэффициентов Фурье имеет вид:

где 0“ - символ Кронекера.

В этом случае поле на выходе дифракционного оптического элемента имеет вид:

E ^{( x} 0 ) = S T n ^{( x} 0 ^)exp [ ^ikng ( ^x 0 ) ] .           ⁽¹⁸⁾

n

Это выражение совпадает с выражением, полученным в работе [7]. Оно приближенно описывает поле в случае, когда размер зоны на ДОЭ меняется слабо. В общем случае метод давал незначительные поправки по сравнению с использованием приближения геометрической оптики [4]. Тогда при расчете надо использовать для коэффициентов Фурье выражения (14), (15)

На рис. 1 - 3 представлены графики интенсивности поля в фокальной плоскости бинарной линзы Френеля, имеющей следующие параметры: апертура – 130 мкм, фокусное расстояние – 134 мкм, высота штрихов - 1 мкм, диэлектрическая проницаемость штрихов – 2.25, длина волны – 1мкм, угол падения – 30°, диэлектрическая проницаемость перед линзой и за линзой – 1. Для расчета поля на рис. 1 был использован дифференциальный метод [8]. Для расчета поля на рис. 2 и 3 был использован метод локальной аппроксимации. Поле за ДОЭ рассчитывалось с использованием интеграла Кирхгофа. Отличие интенсивности в центре во всех рассмотренных случаях составляет несколько процентов, но при использовании метода локальной аппроксимации потребовалось значительно меньше ресурсов оперативной памяти и процессорного времени. Отсутствие высокочастотных биений на последних двух графиках объясняется фильтрующим свойством интеграла Кирхгофа.

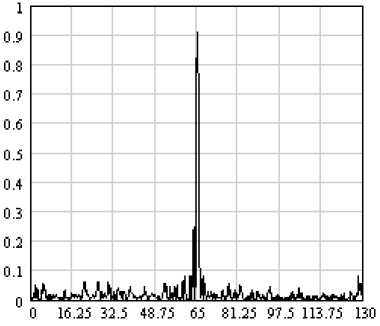
Рис. 1. Интенсивность в фокальной плоскости бинарной

линзы, рассчитанная с использованием

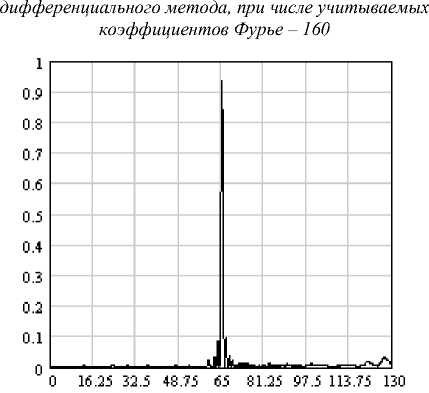
Рис. 2. Интенсивность в фокальной плоскости бинарной

линзы, рассчитанная с использованием метода локальной аппроксимации при числе локальных периодов – 10 и коэффициентов Фурье 60 в каждом периоде

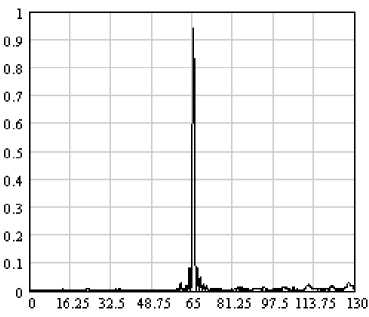
Рис .3. Интенсивность в фокальной плоскости бинарной линзы, рассчитанная с использованием метода локальной аппроксимации при числе локальных периодов – 10 и коэффициентов Фурье 60 в каждом периоде.

• 3. Решение уравнения Гельмгольца в трёхмерном случае

Рассмотрим дифракцию скалярного на объекте, представляющем собой псевдопериодический объект. Предполагаем расположенным в области 0 <  x <  a , где 0 и a – минимальная и максимальная высота слоя. Волновое поле описывается уравнением Гельмгольца:

d2e a2e a2e ,2

—у +--у +--у + k sE — 0. dx2   dy2   dz2

В окрестности (x0, y0), распределение прони- цаемости описывается выражением

^{s ( x} , У , z ) ^— E ^s" ^{( x} 0 ^)exP

n

I n in , ( x - x 0 ) d ₁

x exp

2 ^{n in} 2 ⁽ y - y 0 )

d ₂

где d ₁ d ₂ - периоды по различным осям.

Решение уравнения Гельмгольца в области ДОЭ, в области перед ДОЭ и в области за ДОЭ представим в виде:

E ( x , У , z ) —

• ^— exp ( ik ( a x 0 + A y 0 ) ) E Eⁿⁿ 2 ( ^x 0 , У 0 , z )^x

n ₁, n ₂

x exp [ik (an1 (x - x0 ) + Pn2 (У - У0 ))]

E (x, y, z) — exp (ik (ax 0 + Py 0 ))x xE Inn2 (x0,У0)x n1, n2

x exp [ik (an1 (x - x0) + Pn2 (У - У0)) + ik/nm2z] +

+ exp (ik (ax 0 + Py 0 ))x xE Rn'n2 (x0,У0 )x n1,n2

^x exp [ ik ( ^a n 1 ( ^{x - x} 0 ) + P n 2 ( У ^- У 0 ) ) ^- ik / n , n 2 z ]

E(x, У, z) — exp (ik (ax0 + Py0 )) E Tnn2 (x0, У0 )x n1,n2

^x exp [ ik ( ^a n 1 ( ^{x - x} 0 ) + P n 2 ( У - У 0 ) ) + ik Y nnn 2 z ] .

Коэффициенты I^{n n 2} определяются падающим пучком. Коэффициенты R^{n n 2} , T^{n n 2} и функции E ( x , y , z ) подлежат определению. a m — a + 2 n im/kd 1 , P _n — P + I n in/kd ₂ ,

Ymn — 71 - am1 - P^n .

Подставляя выражение (2 ) в ( 9), получаем систему обыкновенных дифференциальных уравнений для определения функций E^{m m 2} ( x , y , z )

d ² E m ^{1 m 2} ( z )      2

d z 2        ' k ( ^S m , — ' 1 m 2 — 1 2

- ( a ² + a ²) 3 m g m ) E ll ² ( z ) — 0.

Решение системы уравнений аналогично решению системы в пункте .

Поле непосредственно за оптическим элементом

E ( x , y , z ) — exp ( ik ( a x ₀ + p y ₀ ) ) x ^x E T n ^{n 2} ( ^x 0 , У 0 ) exp ( ik Y n,n 2 a )• n , n ₂

Существует случай, когда дифракция на ДОЭ сводится к дифракции на одномерной решетке:

s ( x , У , z ) = £ S ( z )exp

n

2 n in

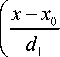
У ^- У о d ₂

u 1 | cos t v J [ - sin t

sin t Y x - x ₀ cos t J( y - y ₀

С помощью преобразования координат:

x = x 0 + u cos t - v sin t , y = y 0 + u sin t + v cos t .

Если угол равен t = - arctg ( d 1 / d ₂ ) ,

^—+ ⁺ "ЗГ = ”72 .

^d 1 ^d 2 ^d

Выражение для диэлектрической проницаемости представляется в виде:

Для дальнейших рассуждений разложим функцию g ( x, y ) в ряд Тейлора.

g(x,У) = g(x0,У0) + |g(x - x0 ) + |g(У - У0 ) + dx 0

⁺ J ^ r ( ^{x - x} 0 )² + ^2- ( y ^- y 0 )² J ^{+ (37)}

• 2 ^ dx0             dy 0

d2g ,

⁺ я я ^{( x - x} 0 ^{)( y - y} 0 ) .

^{d x} 0 ^d y 0

s ( x , z ) = £ S ( z )exp

n

2 n inu d

Пусть t =

. В этом случае функ-

Выражение для поля имеет вид:

E ( u , v , z ) = £ E^nl ( z ) exp [ ik ^u + P _tv ) ] ,    (29)

n , l

E (u, v, z) = ^ I"1 (z) exp [ ik (anu + Ptv) + iky^z ] + n,l                                                 (30)

■ УRnl (z) exp [ik (a„u + Piv) - iky^z], n,l

E ( u , v , z ) = ^ T^nl ( z ) exp [ ik ( a_nu + 0^ ) + iky_riz ] , (31) n , l

ция g ( x, y ) в окрестности точки ( x ₀ , y ₀) имеет вид:

g ^{( x} , y ) = g ^{( x} 0 , y 0 ) + V ( У g ^{( x} 0 , y 0 ) ) 2 u +

+ a ^{( x} 0 , y 0 ) ^{u 2} ₊

1                                 (38)

2 ( b ⁽ x 0 , У 0 ) v ² + 2 c ⁽ x 0 , y 0 ) uv ) .

^d 2 Em'¹, ⁽ z ) + k² ( s m - 1 1 — ( a 2 + a l ) 5 m ) E ( z ) = 0. (32)

В этом случае все направления плоских волн, образующихся при дифракции плоской волны, лежат на конусе ось, которого совпадает с направлением линий дифракционной решетки. Коэффициенты отражения и пропускания находятся из системы линейных уравнений в Приложении 2.

Выражения для коэффициентов приведены в Приложении 3.

Рассмотрим случай когда c=0, что соответствует переходу к случаю радиальной симметрии. В этом случае функция g ( x, y ) в окрестности точки ( x 0 , y 0 ) имеет вид:

g ^{( x} , y ) = g ^{( x} 0 , y 0 ) ⁺ V (^y g ^{( x} 0 , y 0 ) ) ^{2 u +}

⁺ 2 ( a ^{( x} 0 , y 0 ) ^{u 2 +} b ^{( x} 0 , у 0 ) ^{v 2} ) .

Выражение для Фурье коэффициентов цаемости принимают вид:

S n = E g m ⁽ x 0 , У 0 ^)exp ( ikg ⁽ x 0 , У 0 ) )^X

прони-

4. Дифракция на двумерных зонных структурах

Пусть волна с комплексной амплитудой E ( x ) = K ( x , y ) exp ( ik ф (x , y ) ) падает на область с проницаемостью в виде:

x exp

m

r

- ik

D 1

s ( x , У , z ) = ^ gⁿ ( z ) exp[ ikng ( x , y )].           (33)

n

Выберем систему координат таким образом, чтобы ось совпадала по направлению с градиентом функции g ( x , y )

u

^ e v

у g ⁽ x , У )

V (^y g ⁽ x , У ) ) ²

^ ^

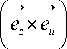
где e_u , e_v - базисные вектора новой системы коорди-

нат. Преобразование координат имеет вид:

x 1 | x ₀ 1 | cos t

У J I y 0 J I ^sin t

- sin t cos t

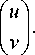
Обратное преобразование имеет вид:

( hm - to _n ) 2 am

D ₂

I ^ 1 exp - ik----- d„F, . nl

I     2 bm J

ton - hm am

I d ^ ,

Рассмотрим случай, когда волновое число

стре-

мится к бесконечности ( k ^ да ), но kD 1 ^ const , kD ₂ ^ const . В этом случае F_t = 0 для l * 0 и отличны от нуля только s _{n 0}. В этом случае задача сводится к задаче конической дифракции, рассмотренной в пункте 3.

Рассмотрим теперь падающее поле. Падающее поле в окрестности точки ( x 0 , y 0 ) имеет вид:

E ( u , v ) = K ( x , y ) exp ( ik ^ ( x , y ) ) = K x              (43)

x exp ( ik ^ ( x ₀ + u cos t - v sin t , y ₀ + u sin t + v cos t ) ) .

Разложим функцию ϕ ( x , y ) в окрестности точки ( x 0 , y 0 ) в ряд Тейлора:

ф ⁽ x , У ) = ф ⁽ x 0 , У 0 ) +

1    22      (44)

+ 2 ( ^b 1 ⁽x 0 , У 0 ) v + a 1 ⁽x 0 , У 0 ) u + ² c 1 ⁽ x 0 ,У 0 ) uv ) ,

K ⁽ r ^)exp ( ^ik ф ⁽ r ) )     ( to ² )

----------------exp — ik-n- x

D 1        4    2 ц J

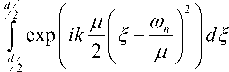
где ф ( x , y ) = ф ( x 0 , y 0 ) + eu + fv.

Выражения для коэффициентов приведены в Приложении 3.

Разложим функцию K exp ( ik ф (x , y ) ) в квазипе-

дg D д g     дф     д2ф где a = —, р = —т, у = —, ц = —т д r0        д r0        д r0        д r0

.

риодический ряд Фурье:

K exp ( ik ф ( x , y ) ) =

= E I nn exp [ ik ( a n u + p n 2 v ) + ik / ^n 2 z ] ’ n ₁, n ₂

где

I" = DD И K ⁽ x- у • '

x exp

x exp

%

ik ( ^b i ^{( x} 0 , У 0 ) v ²

— ik

= e +

2 n n 1 u

kD ₁

2 n n 1 kD ₁

+ a i ( x 0 , У 0 ) u ² + 2 C i ( x 0 , y 0 ) uv )

2 n n ₂ v

kD ₂

dudv ,

x

, P n 2 = f +

2 n n ₂

. kD ₂

Используем формулы для расчета поля на одномерной дифракционной решетке, полученные в пункте 1, и, переходя от координат ( u, v ) к ( x, y ), получаем поле непосредственно за слоем в окрестности точки ( x 0 , y 0 ). Поле на расстоянии от слоя можно получить, применяя метод Кирхгофа([1]-[3]). Полученные формулы имеют асимптотический характер. Достоинство данного подхода к расчету поля состоит в том, что удалось свести двумерную задачу дифракции свести к нескольким задачам дифракции на одномерной дифракционной решетке значительно меньшей размерности и вычислительной сложности. В результате появилась возможность рассчитывать поле от дифракционных оптических элементов, апертура которых составляет несколько тысяч длин волн. Это позволит рассчитывать характеристики оптических систем, содержащих дифракционные оптические элементы.

В качестве примера рассмотрим дифракцию радиально-симметричной скалярной волны на радиально-симметричном объекте. В этом случае разложения имеют вид:

(    4     (      ^д g ( ' 0 ) v_1 ^д g ( ' 0 ) 2.,

g(x,У) = g(r0)+   ---u +7 a 2 u + д r0      2  д r0

1 '" g i r l

2 r

d r ²

v ² (46)

ф ^{( x} , У ) = Ф 0 ^{( r} 0 ) ⁺ ^ ⁽ r 0 ) ^{u + д} r

¹ IV ^ф 0 ( ' 0 ) 2      ¹

--;—- u +-- 2 д г ,²           2 г.

^ф 0 ( ' 0 ) _v 2

д r,²       ’

где ^r 0 = xx 0 + y 0 .

Рассмотрим теперь

асимптотический

k ^ го , kD 1 ^ const , kD ₂ ^ const . В этом

случай случае

Заключение

В работе предложен метод решения задачи дифракции в случае, когда объект представляет собой дифракционный оптический элемент, обладающий зонной структурой. Получено, что в случае, когда k ^ го задача дифракции произвольной волны сводится к решению задачи конической дифракции на решетке. Это позволяет значительно уменьшить вычислительную сложность при численной реализации методов решения задач дифракции. Предложенный метод позволяет оценить параметры волнового поля без использования суперкомпьютеров.

В дальнейшем предполагается использовать аналогичный подход для решения задач в рамках векторной электромагнитной теории.

задача сводится к дифракции нескольких плоских волн на одномерной дифракционной решетке. Выражения для Фурье коэффициентов проницаемости

и падающего поля имеют вид:

^£ n = TT E g m ^{( r} 0 ) exp ( ikg ^{( r} 0 ) ) ^x

^D 1 m

x exp — ik

( a m — to n ) .    ^{2 e} m

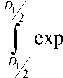
ik p m 2

to n — a m I

p m

d § ,

Приложение 1

Решение уравнения имеет вид:

Em = E(akexp(ikkkz) + bkexp(—ikXk (z — a)))em , k где ek и λk - собственные вектора и собственные числа матрицы (Em_ 1 — ol 8m) ek = XX ek .

Поле внутри дифракционной решетки имеет вид:

E ( x, z ) = exp ( ikax ₀ ) E ( a_k exp ( ikX k z ) +

n bkexP (— ikXk (z — a))) eknexP (ikan (x — x0)).

Коэффициенты отражения и пропускания находятся из системы линейных уравнений

Z ( 5" „ R^k ( % о ) - ea -

• -    e k exp ( ikM ) b^k + 5" „ T^k ( % о ) ) - - I n ( % о ) ,

Z (-p„5 „R^k ( x о ) -X ... -

-X k e k exp( ik X k d ) b k +5 T ( x 0 )) = -₽ „ I " ( x 0 ), Z ( _§k R^k ( x о ) + e k exp ( ,d ) a^k ■ eb -

• -    S n exp ( ike_kd ) T^k ( x о ) ) - о,

Z ( 5 R ( x о ) + Vnexp ( vd ) a^k -

• -    /. b - e k exp ( ike k d ) 5^ ( x о ) ) - о.

Приложение 2

„ nkl     nil

(5kR - eka - k

• -    e k exp ( ik к ki a ) b^k + 5 " T^kl ) - - I n ,

Z ( " e „i 5 k X l - X ki e n a" - k

- X ki e kl exp ( ) b^kl + 8 „ 1^И ) - - в^¹ ,

Z ( ⁵ „ R^{k +e}‘ ki ^exP ( ^ikk ki ^a ) a “ ⁺ k

• + . b - 5 k exp ( ikM ) T^k l ) - о,

Z ( о ■ 5 „ R^kl + V^P ( ikk_Ha ) a^k - k

• - '    b - e ki exp ( ike_k i a ) 5 J ) - о.

Здесь суммирование по индексу l не производится, и система уравнений распадается на несколько систем уравнений меньшей размерности.

Приложение 3

d ² g a x о a y, a ² g

(       \ d² g ₂    d² g . ₂

a (xо yо) - , cos t + тгsin t + ax о          ay о sin2t, 0

b(x₀ y₀)- ^—g sin ² t + ^—g cos ²

( о ’ ) dx 2

t -

a ^x о a y

sin2 t , 0

d 2           d 2

c x y = g sin2 t + g sin2 t+ 2    g cos2 t ,

( о -Ло) axо          ayо             axо ayо fag         ag . । e- I —— cos t+ —— sin t I, (ax о       ay о dg         dg . |

----cos t --sin t I , a y о        a ^x о )

• a,    (x₀ y₀) = ^- ^ cos ² 2 1 + ^d- ^ sin ² 2 1+ ^d ^ sin 2 1 , ^{1 ( о} '     ) d x о²              a y о²             d x о a y о

, / x a² ф . ₂     <'2 ф     ₂. a² ф .

• b ,    ( x„ , y ,,) - ——sin t+ —- cos t --sin2 1 ,

• ¹              d x о²            a y о²            d x о a y о

  / л a² ф . „ а² ф -       „ a² ф

c . ( x _n, y _n) - —f-sin2 1+ — k-sin2 1 - 2-------cos2 1 .

1 00 22

a ^x о          a y о           a ^x о a y о

Работа выполнена при поддержке российско– американской программы «Фундаментальные исследования и высшее образование» («BRHE»), а так же грантов РФФИ №№ 03-01-00109, 04-07-90149 и 04-01-96517.