Асимптотические режимы гидродинамического контакта упругого цилиндра и жесткого полупространства

Одной из основных задач гидродинамической теории смазки является определение толщины смазочной пленки между контактирующими телами. Расчетные значения толщины пленки в тяжело нагруженных гидродинамических контактах жестких тел оказываются нереально малыми. Чтобы расчеты соответствовали действительности, нужно учитывать деформацию тел в зоне контакта, и заметный рост вязкости смазочного материала, с повышением давления. Теория смазки, учитывающая перечисленные явления, называется контактной гидродинамикой или упругогидродипамической теорией смазки. Контактная гидродинамика. как наука, возникла, в работах А. М. Эртеля, А. Н. Грубина и А. И. Петрусевича в 1945-1951 гг. и впоследствии развивалась в работах многих авторов. Так, в 1989 г. Биссет [1] впервые получил согласованное асимптотическое решение задачи упругогидродинамической теории смазки, вязкость которой растет умеренными темпами с увеличением давления. В настоящей работе исследуется асимптотическая структура, течения смазочной жидкости для некоторых предельных ситуаций тяжело нагруженного гидродинамического контакта, упругого цилиндра, и жесткого полупространства. В соответствии с классификацией Джонсона. [2] выделяются различные асимптотические режимы упругогидродинамической смазки. Уточняются диапазоны применимости ряда, формул для расчета, толщины смазочной пленки.

Рассмотрим плоскую стационарную задачу о качении бесконечного упругого цилиндра, радиуса R по жесткому неподвижному полупространству, на которое нанесена вязкая жидкость (рис. 1). Цилиндр движется со скоростью U относительно полупространства и вращается с угловой скоростью ш относительно своей оси. К рассматриваемой задаче сводится задача о гидродинамическом контакте бесконечных упругих цилиндров. С областью гидродинамического контакта, цилиндра, и полупространства, свяжем прямоугольную систему координат хуг (ось у направим вдоль оси цилиндра, ось г — перпендикулярно контакту, а ось х — в направлении, противоположном направлению качения цилиндра).

Поверхности цилиндра и полупространства разделяет смазочная пленка П = {(х,г) : 0 6 г 6 ^(х),а 6 х 6 с}, г де К(х) — толщин а пленки, х = а и х = с — входная и выходная границы области гидродинамического контакта, в выбранной системе координат. Предполагается, что пленка, тонкая, т.е. характерное значение толщины пленки

Рис. 1. Качение упругого цилиндра по жесткому полупространству при наличии смазки

Һ * много меньше характерного размера I * области контакта ( һ * << I * ) а сам этот размер много меньше радиуса цилиндра ( I * << R )

Внутри смазочной пленки плотность жидкости р и составляющие скорости частицы жидкости и и w удовлетворяют уравнению неразрывности:

дЩм) д(pw) _ Эх + дг '

Уравнение ползущего движения ньютоновской жидкости в тонкой пленке при числах Рейнольдса Re = рШ* / р <<  ( I * / Һ * )² имеет вид [3]

dp дт dx дг

д Эи дг р дг '

где р(х) — контактное давление, отсчитываемое от атмосферного (поперек пленки давление не изменяется); т = рди/дг — касательное напряжение в смазочной пленке; р — динамическая вязкость жидкости.

Смазочную жидкость можно считать ньютоновской, если характерное время пребывания частицы жидкости внутри области контакта t * = I * / Ш много больше времени релаксации t_T = р/G^ где G — модуль сдвига жидкости, и при этом не очень велики скорости сдвига [3]: t_T 1ди / дг | << 1. Возможность использования уравнения (2) также обусловлена малостью производной dh/dx и тем, что силы инерции, действующие на смазочный материал, малы по сравнению с силами вязкого трения, если так называемое приведенное число Рейнольдса Re* = рШҺ * ( р1 * ) много меньше единицы.

Уравнение энергии в приближении тонкой смазочной пленки принимает вид [3]

рср ^ ) - А к») . (3) дх дг) дг \ дг) дг dx где ср — удельная теплоемкость жидкости при постоянном давлении; Т — абсолютная температура; к — коэффициент теплопроводности; 3 — коэффициент объемного теплового расширения. Первое слагаемое в правой части уравнения энергии (3) представляет собой тепловыделение за счет вязкой диссипации, второе слагаемое — тепловыделение от сжатия.

Вязкость р смазочной жидкости сильно растет с увеличением давления р и значительно падает с ростом температуры Т: р = р ( р,Т ). Зависимость вязкости от давления обычно аппроксимируется экспонентой (закон Баруса) [3]

р ( р,Т ) = ро exp(ap),

где а = а ( Т ) — пьезокоэффициент вязкости, ро = ро ( Т ) — вязкость при р = 0.

При высоких контактных давлениях проявляется сжимаемость жидкости — умеренный рост ее плотности с увеличением давления [4]: р = p(p). Поскольку коэффициент /3 объемного теплового расширения жидкости мал, изменением плотности поперек смазочной пленки можно пренебречь.

Из уравнения неразрывности (1) следует, что массовый расход жидкости т одинаков в каждом поперечном сечении:

т = р

к ( х )

J udz = const.

В изотермическом приближении (которое и будет в дальнейшем рассматриваться) вязкость постоянна, поперек смазочной пленки (вместе с давлением и плотностью). Последовательное интегрирование по z уравнения (2) с учетом прилипания жидкости к поверхностям цилиндра, и полупространства, позволяет получить распределение продольной составляющей скорости по толщине пленки в рассматриваемой системе координат:

и =

z ( z — h) dp

2ц dx

+ ( uR — U )^z + U.

Обозначая Uo = (U + шК )(2 и подставляя (6) в (5), приходим к уравнению Рейнольдса для распределения давления в тонкой смазочной пленке:

dp -и/^—т/р, x е (а,с) dxh

Если плотность жидкости постоянна, что также будет предполагаться в дальнейшем, то уравнение Рейнольдса, для несжимаемой жидкости принимает вид [3]

= 12^Uo Һ—Ь°, x е (a,c),(8)

dxh где ho = m/(pUo) — расходное значение толщины смазочной пленки.

При контактных давлениях, значительно превышающих (по модулю) возможные капиллярные давления и напряжение разрыва, жидкости, граничные условия для уравнения Рейнольдса (8) имеют вид

p(a) = p(c) = 0.                                          (9)

На выходной границе области нагруженного контакта, дополнительно задается так называемое кавитационное [3], или рейнолъдсово, условие dp(c)/dx = 0, которое вместе с условиями (9) позволяет определить c и расходную толщину ho, если величина а известна, а также обеспечивает неотрицательные давления в расходящейся части пленки. Согласно уравнению Рейнольдса (8) условие dp(c)/dx = 0 эквивалент но условию h(c) = ho.

Выражение, задающее профиль зазора, между цилиндром и основанием, с учетом упругих перемещений точек поверхности цилиндра под действием давления p(x) и при условии, что размеры области контакта малы по сравнению с радиусом цилиндра (|а| <<  R, c << R). имеет вид [3]

„ i    x2 — c2    4 Г h = ^ R + iE J p(i)ln

a

^{c —} € € — x

d€,

где E ‘ = 2 E /(1 — v ²), v и E — коэффициент Пуассона и модуль упругости материала цилиндра. При выводе соотношения (10) учитывалось условие h(c) = ho.

Давление, действуя на поверхность цилиндра, создает усилие Wz, приходящееся на единицу длины цилиндра, которое компенсирует внешнюю нагрузку W, приложенную к ци линдру:

С

W = W_z = J p ( x ) dx.

(И)

a

Таким образом, даже в изотермическом приближении задача, о течении несжимаемой смазочной жидкости в тонком зазоре между упругим цилиндром и жестким полупространством представляет собой нелинейную интегродифференциальную систему, состоящую из взаимосвязанных между собой дифференциального уравнения гидродинамики (8), интегрального уравнения теории упругости (10), граничных условий (9) для этих уравнений (в том числе на. неизвестной границе), выражения для вязкости (4) и условия нормировки (И).

Важным этапом решения этой системы является нахождение минимальной толщины ^min смазочной пленки, значение которой, как правило, не намного отличается от расходного значения ко- Как следует из анализа [4] уравнения Рейнольдса (8) с учетом зависимости (4), расходное значение ко толщины пленки определяется максимальным входным приведенным градиентом контактного давления exp( — аp ) dp / dx.

3.    Асимптотический анализ

В работе [5] был проведён асимптотический анализ задачи о гидродинамическом контакте цилиндра, с упругим покрытием и жесткого полупространства, в практически важном случае больших нагрузок W на единицу длины цилиндра. Изложенный в этой работе асимптотический метод естественно попытаться применить для анализа течения смазочной жидкости между упругим цилиндром и жестким полупространством.

Перейдем в системе (8) - (П), (4) к безразмерным переменным, взяв в качестве характерных масштабов параметры сухого упругого контакта, цилиндра, и полупространства, рассчитываемые по теории Герца (см., например, [3]). Отнесем линейные размеры ж, а и с к герцевой полуширине контакта Ь* = ^8WR/(—Е') давление р к максимальному герцеву давлению р* = у/ WE'/(2—R), толщ ины h, hmin и ко к ф = Ь*/(2R). Тогда система уравнений (8) - (И), (4) в случае обильной подачи смазочного материала в контакт (|а| >> с, но достаточно потребовать, чтобы h(a) >> ко) примет вид exp(—Qop) ^ = Го dx

^{h — к} о

, 3   , ^ж € ⁽ ^,сі,

h — ho = x² — с²

+ -—

---------------------I

с

/ р(е)Ы ^

^{с - е}

е -

x

de,

р⁽ ^ : = р^{( с )} = о,

с /

— га

p ( x ) dx = —.

Видно, что безразмерная система. (12) - (15) содержит только два. параметра, (также безразмерных):

_{п           v} 48_№UR²   7,702h_m        /р * \²

Qo = ар * и Го =           =--------= 7, 338       ,

р*Ь³          й *             рРт)

где һ_т = 4,895ц₀U₀R/W и р_т = 0,1986у/ W /(ц₀U₀)W/R — соответственно (согласно [3]) минимальная толщина, смазочной плёнки и максимальное гидродинамическое давление, характеризующие течение жидкости постоянной вязкости между жёстким цилиндром и жестким основанием. Цилиндр можно считать жестким, а. вязкость постоянной, если к т / й * = о, 130Го >> 1, ар т = 2, 7O9Qo/\Г << 1,что соответствует режиму изовязкой смазки жестких тел (режим IVR) по классификации Джонсона [2].

Практически важному случаю тяжело нагруженного гидродинамического контакта, упругого цилиндра и полупространства в плоскости параметров Qo и Го соответствует подобласть, определяемая условием Го << 1. И в этой подобласти можно выделить следующие асимптотические режимы смазки:

• 1)    обобщенный режим изовязкой смазки упругих тел (обобщенный режим IVE: допускаются умеренные темпы роста вязкости с увеличением давления): Го << 1, QoГ0^1/5<< 1

• 2)    режим пьезовязкой смазки упругих тел (режим PVE: вязкость успевает существенно вырасти, прежде чем входной приведенный градиент давления достигнет максимума): V << 1, QoVo^1/5 >> 1, QoV << 1.

Течение жидкости между упругим цилиндром и полупространством для каждого из указанных режимов естественным образом разбивается на. ряд примыкающих друг к другу участков, количество и характерные особенности которых зависят от конкретной асимптотической (предельной) ситуации. Но во всех случаях неизменно присутствуют два. участка:

• а)    центральный (несущий) участок высоких давлений. Его линейные размеры и распределение давления в главном приближении определяются условиями сухого контакта, упругого цилиндра, и основания [3]:

p(x) = V1 — x2, |x| < 1, 1 — |x| = 0(1), с = 1.

Внутри центрального участка, толщина, пленки практически постоянна, (деформированная поверхность цилиндра, почти параллельна, основанию) и равна, своему расходному значению ho: |h — ho| << ho, причем разность |h — ho| экспоненциально мала, если Qo >> 1;

• б)    входной участок низких давлений, на. котором наблюдается безрасходное течение несжимаемой жидкости постоянной вязкости

  dp dx

  
  

, x <  —1,   |x + 1| — 0(1)

h2

в сужающемся зазоре вне сухого упругого контакта, цилиндра, и основания [3]:

h ( x ) = |x| Vx² — 1 — ln(|x| + Vx² — 1), x < —1,   |x + 1| = 0(1).

Согласно этим соотношениям и граничному условию (14) в зоне перекрытия входного и следующего за ним участка (то есть при x ^ —1 — 0)

^h(x) ~      ^{|x + 1|3/2,} P^(x) ~ 777^9V4t2 .                        (¹⁶)

• ³                     64(x + 1)

Обобщенный режим изовязкой смазки упругих тел содержит в себе две предельные (асимптотические) ситуации:

• 1.1)    изовязкая смазка, упругих тел (режим IVE: вязкость смазочной жидкости постоянна, внутри области упругогидродинамического контакта): V << 1; Qo << 1

• 1.2)    вязкость существенно увеличивается с ростом давления, но входной градиент давления успевает достигнуть максимума, прежде чем становится заметным изменение вязкости: И << 1, Qo >> 1, QoV 1 / 5 << 1;

В случае изовязкой смазки упругих тел согласно [1] можно выделить два малых слоя (переходный и выходной), окаймляющих центральный участок, внутри которых безразмер-1/5

ное давление p является величиной порядка V > а безразмерная толщина h и ее изменение 3/5                                                 2/5

имеют порядок И • Размеры этих слоев порядка V) . При этом подачу смазочного материала. в контакт можно считать обильной, если размеры входного участка, значительно превосходят размеры переходного слоя: |а| — 1 >> И)2/5. Расходная толщина ho формируется в переходном слое, где наблюдается максимум входного градиента, давления, а. в выходном слое толщина пленки достигает минимального значения hmin. Числовые коэф-3/5

фициенты при V)' в выражениях для безразмерных расходной ho и минимальной hmin толщин пленки находим из сопоставления результатов данного асимптотического анализа, с результатами численного решения задачи упругогидродинамической теории несжимаемой смазки, впервые полученного Херребрухом [6]:

hmin = 0, 8 ho =0, 31 Vo3/5, что вполне согласуется с результатами Биссета. [1].

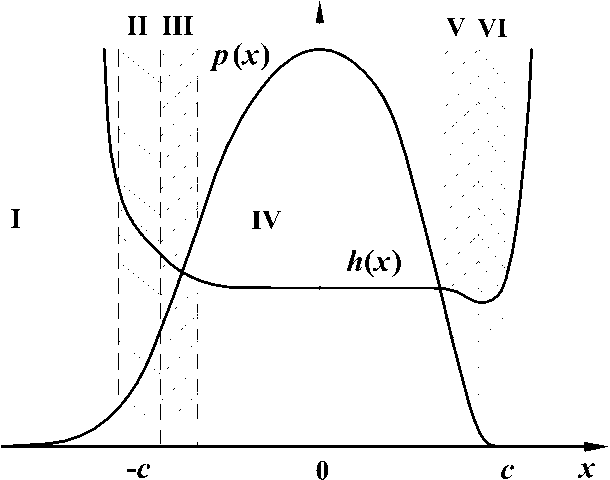
Рис. 2. Характерные участки области упругогидродинамического контакта

В асимптотической ситуации 1.2), соответствующей условиям: V0 << 1, Q_o >>  1, 1/5

QoV ⁷ << 1, дополнительно возникают еще два участка, отделяющие переходный и выходной слои от центрального участка (рис. 2). Внутри этих участков «включается» и «выключается» зависимость (4) вязкости от давления, а безразмерное давление р имеет порядок 1 /Q_o >>  ^01/5• В переходном и выходном слоях вязкость практически постоянна и равна своему значению при нормальных условиях. Поэтому расходное и минимальное значения толщины пленки оказываются такими же, как и в предыдущем случае, что позволяет рассматривать обе асимптотические ситуации совместно как обобщенный режим изовязкой смазки упругих тел (обобщенный режим IVE).

1/5

На режиме пьезовязкои смазки упругих тел (режим PVE: V_o<<  1 Qo Vo >> 1, Q_oV0 << 1) переходный и выходной слои меняются местами с участками «включения» и «выключения» зависимости (4) вязкости от давления. Размеры этих участков имеют порядок VQoVo << 1, поэтому подачу смазочного материала в контакт можно считать обильной, если |п| — 1 >>  V Q_oVo. Расходная толщина h_o формируется на участке «включения» зависимости (4), а на участке «выключения» зависимости (4) толщина пленки достигает своего минимального значения hmin. Значение безразмерной толщины ho определяется из интегрального соотношения:

-1

Г ^h — ^ho

J   h^{3 dx} = 1’

-∞ где согласно (16), но уже с учетом ho

һ(ж) — ho » 13^|ж + 1|³/², ж< —1, ж + 1 = O ( VQo Vo).

Откуда получаем известный результат [3]:

= 9 (2^3) / (QoVo)3/4 = 0,2718(QoVo)3/4.

При этом hmin = 0, 7476ho.

Характерной особенностью режима пьезовязкой смазки упругих тел является наличие крутого пика (второго максимума) давления [3] в зоне сужения пленки на выходе из контакта. В случае обобщенного режима изовязкой смазки упругих тел второй максимум давления отсутствует [6, 1].

Таким образом, толщина смазочной пленки формируется в зоне входа, точнее на малом участке, расположенном между входной зоной низких давлений и областью высоких давлений, и существенно зависит от того, успевает ли заметно измениться вязкость, прежде чем входной градиент давления достигнет максимума. Для минимальной толщины пленки ^min справедливы следующие приближенные выражения (возвращаемся к размерным переменным):

• 1)    обобщенный режим обильной изовязкой смазки упругих тел (обобщенный режим IVE): V << 1, QoV0/5<< 1, |а| - с >> V₀^2/5b*, bm™ = 0, 8^0 = 0, 31V₀^3/5d*;

• 2)    режим обильной пьезовязкой смазки упругих тел (режим PVE): V << 1; QoVo^1/5 >> 1, Q0V0 << 1, Ы - с >> VQo», U. = 0, 7476^ = 0, 2O3(QoV))^3/4d*.

4.    Влияние тепловыделения и сжимаемости жидкости на толщину смазочной пленки 5.    Выводы

Из представленных выражений для толщины пленки на. различных режимах смазки следует, что даже при использовании жидкости постоянной вязкости (Qo << 1) смазочная пленка в тяжело нагруженном гидродинамическом контакте (V << 1) упругого цилиндра. и жесткого полупространства, оказывается существенно более толстой (режим IVE), чем пленка, разделяющая жёсткий цилиндр и жёсткое полупространство (режим IVR). С другой стороны, смазочные материалы с большим пьезокоэффициентом вязкости (режим PVE: Q₀V1/⁵ >> 1, QoVq << 1) обеспечивают существенно большую толщину смазочной пленки, чем жидкости постоянной вязкости (Qo << 1).

Для полноты изложения следует отметить, что при качении жесткого цилиндра, по жесткому основанию, на. которое нанесена, жидкость с большим пьезокоэффициентом вязкости [2], ^min = 0,816^0 = 1,666[(ацо^о)²^]^1/3- На самом деле, последнюю формулу можно применять, если толщина смазочной пленки с большим пьезокоэффициентом вязкости существенно превышает упругие деформации поверхности цилиндра. — обобщенный режим пьезовязкой смазки жестких тел (обобщенный режим PVR): Фпіп/Ф = 0, 252(QoVo)^2/3 >> 1, Q_Pm = 2, 709Qo/V^ >> 1.

Если скорость качения цилиндра и нагрузка, прижимающая его к полупространству, значительны, то согласно уравнению энергии (3) в смазочной пленке происходит интенсивное тепловыделение вследствие вязкой диссипации и сжатия, а также передача тепла за счет теплопроводности (поперек пленки) и конвекции. Все это приводит к нагреву поверхностей тел и смазочного материала, в области контакта, и, следовательно, к изменению вязкости жидкости, в том числе и поперек смазочной пленки. Уравнение Рейнольдса. (7) при этом должно быть заменено своим тепловым аналогом [3].

Прогрев в зоне входа, где формируется смазочная пленка, приводит к снижению вязкости смазки, поступающей в контакт, и, следовательно, к уменьшению толщины пленки [3] во всей области контакта. Из анализа, порядков членов в уравнении движения жидкости (2) ив уравнении энергии (3) следует [7], что выделение тепла, на. входе за. счет вязкой диссипации мало влияет на толщину пленки, если U2\d^o ( T )/dT \ / к << 1.

В центральной зоне высоких давлений в соответствии с выражением (4) резко возрастает вязкость смазочной жидкости. Если качение сопровождается проскальзыванием (U = шД), то из-за малости толщины смазочной пленки в центральной зоне наблюдаются большие скорости сдвига, что в силу высокой вязкости приводит к значительным касательным напряжениям и, следовательно, к более интенсивному тепловыделению, чем при чистом качении. В таких экстремальных условиях имеет место неныотоновское поведение смазки. Рост вязкости сопровождается значительным увеличением времен релаксации t_T = ц/G, вследствие чего в зоне высоких давлений начинают проявляться вязко упругие свойства смазочного материала (при небольших скоростях сдвига). С увеличением проскальзывания зависимость касательного напряжения от скорости сдвига становится нелинейной. Однако смазочная пленка, образуется в зоне входа, где давления относительно невелики, поэтому неныотоновское поведение и сдвиговый разогрев в области параллельности смазываемых поверхностей уже не могут существенно изменить толщину пленки.

Как отмечалось ранее, непосредственно сжимаемость жидкости умеренно проявляется лишь при высоких давлениях [4], что согласно уравнению Рейнольдса (7), учитывающему рост плотности р = р(р) с увеличением давления р. приводит к некоторому утончению смазочной пленки в центральной зоне тяжело нагруженного контакта [1]: Һ = Л(с)р(О)/р(р).

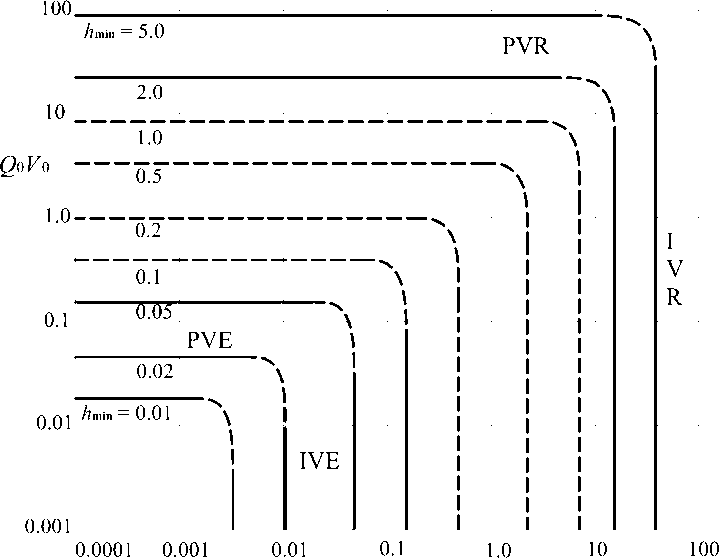
Совместный эффект упругих деформаций и переменной вязкости состоит в возрастании минимальной толщины смазочной пленки. При этом на режимах изовязкой смазки как жестких (IVR), так и упругих тел (обобщенный IVE) безразмерная минимальная толщина пленки hmin/5 * определяется значением одного лишь безразмерного параметра Vq. А на режимах пьезовязкой смазки и жестких (обобщенный PVR), и упругих тел (PVE) h_min /5 * зависит от произведения параметров Q₀ и EQ. Поэтому все четыре указанных режима могут быть наглядно представлены в виде схематической диаграммы (аналог диаграммы Джонсона [2]) в плоскости безразмерных параметров VQ и QqVq (рис. 3). На рис. 3 сплошные линии — линии уровня безразмерной минимальной толщины смазочной пленки hmin/5* для соответствующих асимптотических режимов смазки, пунктирные линии — интерполяция.

Го

Рис. 3. Линии уровня безразмерной минимальной толщины пленки