Асимптотические режимы гидродинамического контакта жестких цилиндров, покрытых тонкими упругими слоями

Определение толщины смазочной пленки между контактирующими телами является одной из основных задач теории смазки. Однако расчетные значения толщины слоя смазки в тяжело нагруженных гидродинамических контактах жестких тел оказываются нереально малыми [1, 2]. Чтобы расчеты соответствовали действительности, необходимо учитывать контактные деформации поверхностей тел, а также значительный рост вязкости смазочного материала при высоких давлениях.

II.    Постановка задачи

Рассмотрим плоскую стационарную задачу о качении с проскальзыванием бесконечного цилиндра радиуса R по тонкому слою вязкой несжимаемой жидкости, нанесенному на жесткое неподвижное полупространство (см. рис. 1). Цилиндр движется со скоростью U относительно полупространства (справа налево в плоскости рисунка) и вращается с угловой скоростью ш относительно своей оси. К рассматриваемой задаче сводится задача о гидродинамическом контакте бесконечных цилиндров. С областью гидродинамического контакта цилиндра и полупространства свяжем декартову систему координат Oxyz (ось Oy направим вдоль оси цилиндра, ось Oz — перпендикулярно контакту, а ось Ox — в направлении, противоположном направлению качения цилиндра).

В выбранной системе координат распределение давления в тонком слое смазочной жидкости, разделяющем цилиндр и полупространство (т. е. внутри области гидродинамического контакта), описывается одномерным стационарным уравнением Рейнольдса [1]:

dp h - h 0

dx = ¹² ^u _h 3 , x ^{e (} a,c ) ,        (!)

где p ( x ) — контактное давление, отсчитываемое от атмосферного; ц — динамическая вязкость жидкости; u = U +2 ^R — полусумма скоростей поверхностей контактирующих тел относительно указанной системы координат (заметим, что в случае чистого качения цилиндра (без проскальзывания) u = U = wR ); h ( x ) — толщина слоя жидкости; h 0 — ее расходное значение h o 0 = quo, где q 0 — расход жидкости между контактирующими телами); x = а и x = c — входная и выходная границы области гидродинамического контакта.

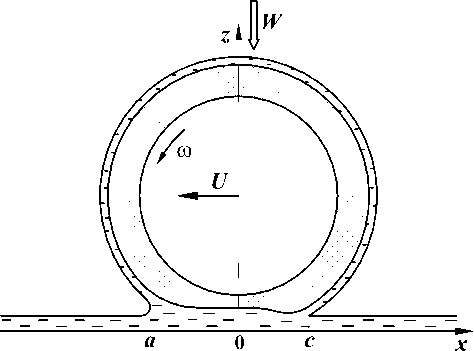
Рис. 1. Качение цилиндра по слою жидкости

При контактных давлениях, значительно превышающих (по модулю) возможные капиллярные давления и напряжение разрыва жидкости, граничные условия для уравнения Рейнольдса (1) имеют вид [1]:

Р ^{( а} )= Р^(c )= ddxc) = ⁰ •          (²)

Величина а обычно считается заданной, c и h о подлежат определению. Вместо а может быть задан расход q о = uh ₀, при этом а и c — неизвестны.

Вязкость д смазывающей жидкости сильно растет с увеличением давления p и значительно падает с ростом температуры T: д = д ( p, T ). В изотермическом приближении (которое и будет в дальнейшем рассматриваться) зависимость вязкости от давления аппроксимируется экспонентой (закон Бар уса) [1]:

Д ( p )= Д о exp( ap ) ,              (3)

где a — пьезокоэффициент вязкости, д о — вязкость при p = 0 (напомним, что давление отсчитывается от атмосферного).

Цилиндр имеет тонкое упругое покрытие, поэтому деформация поверхности цилиндра пропорциональна локальному контактному давлению. Учитывая также малость ширины области кон такта по сравнению с радиусом цилиндра, для толщины смазочного слоя получим (см. рис. 2):

h ⁽ x ) = z о + x- + Cp ⁽ x ) , x € ⁽ a, c ) ,     (4)

2 R zо — координата по оси Oz (аппликата) точки не-деформированной поверхности цилиндра, соответствующей x = 0 (z = 0 соответствует поверхности полупространства); C — упругая постоянная покрытия цилиндра:

C =

(1 + v )(1 — 2 v ) (1 — v ) E

δ C ^,

где 8 с — толщина слоя покрытия, v и E — коэффициент Пуассона и модуль упругости материала покрытия. Предполагается, что коэффициент Пуассона меньше 0,5.

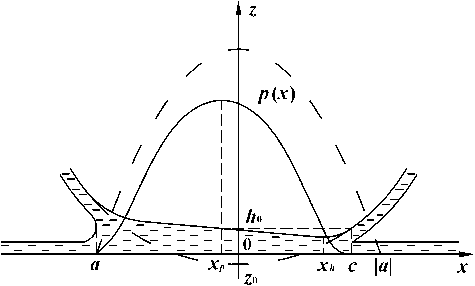
Рис. 2. Слой жидкости между поверхностями

Давление, действуя на поверхность цилиндра, создает усилие Wz, приходящееся на единицу длины цилиндра вдоль оси Oy, которое компенсирует внешнюю нагрузку W, приложенную к ци линдру:

W = W z

c jp (x) dx.

a

Величина W, как правило, задается, a z0 под лежит определению.

Таким образом, задача о контакте цилиндра с упругим покрытием и жесткого полупространства при наличии смазочного слоя заключается в совместном решении уравнений (1) и (4) с учетом выражения (3), граничных условий (2) и условия нормировки (5).

III.    Качественный анализ

Качественный анализ системы (1) - (5), проведённый в работе [3] в предположении об ограниченности и достаточной гладкости p ( x ) и строгой положительности h ( x ) внутри области упругогидродинамического (УГД) контакта, позволил установить следующие важные результаты (см. рис. 2), которые вытекают из существования решения системы (1) - (5):

• 1)    a <  0, c >  0, |a| > c;

• 2)    давление p ( x ) строго положительно на ( a, c ), монотонно возрастает на ( а, x_p ) от нуля до максимального значения p max = p ( x p ) = ( c ² — — x p ) / (2 CR ) >  0, x p E ( —c, 0), г де xp — точка строгого максимума давления, и монотонно убывает от p max до нуля на ( x_p ,c ). При этом справедлива оценка сверху: p ( x ) <  ( а ² — — x ²) / (2 CR), x E ( a,c );

• 3)    толщина смазочной пленки h ( x ) монотонно падает от h ( а ) до минимального значения h min = = h ( x h ) на ( a,x_h ), 0 < x_h< c, где x h — точка строгого минимума толщины пленки, и монотонно возрастает от h min до h о = h ( x_p ) = h ( c ) на ( x h ,c ), при этом h ( x ) < h ( a ), x E ( a, c );

• 4)    (2 |a| — c )( |a| + c ) ² >  4 b 3, откуда |a| > b * , где b * = Ц3 CWR/ 2 — полуширина области сухого контакта цилиндра с полупространством. Таким образом, ширина области гидродинамического контакта, по крайней мере, не меньше полуширины области сухого контакта (при прочих равных условиях). Заметим также, что в режиме скудной смазки c ^ b * при a ^ —b * — ^— 0

• 5)    W < W_a = 3 CaR^ следовательно, при фиксированном положении входной границы x = a <  0 области У ГД-контакта, как, например, в случае радиального гидродинамического подшипника скольжения с частичным углом охвата, несущая способность смазочного слоя оказывается конечной.

Если профиль h ( x ) зазора между поверхностями, разделенными слоем смазочной жидкости, задан, давление p ( x ) в смазочной пленке находим (прямой метод) интегрируя уравнение Рейнольдса (1) с учетом зависимости (3) и граничных условий (2). С другой стороны (обратный гидродинамический метод Даусона и Хиггинсона [4]), если известно распределение давления p ( x ) в смазочном слое, то согласно (1) и (3) толщина h ( x )

удовлетворяет следующему кубическому уравнению:

IV. Асимптотический анализ

где

d ^П h dx

— 12 ц 0 u ( h — h 0) = 0 ,

x Е ( a, c ) ,

П( x ) =

1 — exp[ —ар ( x )]

α

— приведенное давление, а.

^ = exp( —ар ) dp = 12 ц о      '

dx            dx          h ³

— приведенный градиент давления. Вторая про

изводная приведенного давления равна.

d ²П dx ²

= exp( —ар )

—

/ dp \ ² + d ² р dx     dx ²

= 12 ц 0 и

3h0 — 2h dh h4    dx

В работах [3] и [2] был проведён подробный и согласованный асимптотический анализ системы (1) - (5) в практически важном случае больших нагрузок W на единицу длины цилиндра и обильной подаче смазочного материала, в контакт (|a| ^ b * ). Прежде чем приступить к рассмотрению основных результатов этого анализа, перейдем в системе (1) - (5) к безразмерным переменным: x и c относом к b*. р к р * = 3 W/ (4 b * ). h. h ₀ и z _о iо 5 * = b 2 / (2 R ) = Ср *, цто р * 11 5 * — соответственно максимальное давление и относительное упругое сближение, характеризующие сухой контакт цилиндра, с упругим покрытием и жёсткого основания. Тогда, для режима, обильного смазывания получим

Заметим, что в случае жидкости постоянной вязкости ( ар ^ 1) ц = ц ₀ i1 П( x ) = р ( x ).

Если входная толщина, смазочной пленки h ( a ) >  1 , 5 h о, то в некоторой окрестности входной границы x = a области гидродинамического d П( x )          d ²П( x )

контакта. ' > 0. — 2   > 0 i1 h(x) явля- dx           dx

exp( —Q о р ) d^p dx

h — h _о

h — h о = р + x ² — c ² ,  x Е ( —го, c ) ,

р ^{( х} ) = р ^{( c} ) = ⁰ ,

c j р (x) dx =3 .

-∞

ется наибольшим положительным корнем исследуемого кубического уравнения. В точке x п не-

региба ( d ^П x ^{n )} = 0) восходящего участка эпюры приведенного давления П( x ) входной приведенный d П( x )

градиент давления —dx достигает максимального значения, a h ( x п) является кратным корнем

Видно, что безразмерная система, содержит только два. параметра, (также, естественно, безразмерных):

Q _о = ар * >  0 и

48 ц о uR ² p ∗ b ³ _∗

32 ц о uR Wδ ∗

> 0 .

указанного кубического уравнения, откуда, дим расходную толщину смазочного слоя h о данной эпюре контактного давления:

пахо- по за-

I-

^™

Параметр Q о представляет с<збой отношение р * к давлению 1, при котором существенно возрастает вязкость смазочного материала, (согласно выражению (3)). Параметр

h о=2

3N

4 ц о и           2

/     ( ddp \ = 3 h ⁽ x ^п) '

ENTR (^{exp( —ар} ) dx)

(IVR)

V о = 6 , 537 -min- δ _∗

4 , 488

(

p ∗

(IVR) p max

)

На интервале ( x _п ,x_p ) h ( x ) >  0 является уже меньшим положительным («средним») корнем, а.

d П( x )

на. промежутке ( x_p,c ). гдс dX <  0. — единственным вещественным корнем рассматриваемого кубического уравнения. При этом точка x ^ ми-

где hmmVR =0,816hГ° = 4, 895 ^WR,

(IVR)         V2RhLT)        Wv" W рmax = 1, 521 цоu (ivr)x2 = 0, 1986\ n u "ft

^{( h} min ⁾²            V ^ц°^{u R}

пимума толщины слоя жидкости является одпов-

ременно точкой еще одного перегиба. (

d ²П( X h )

dx ²

= 0) функции П( x ), в которой приведенный гра- d П( x )

диент давления — dx также достигает минимального значения:

min fexp( —ар )   ^ = 12 ц_ои min ---⁰

EXIT            dx        ⁰     h ³ _min

Отметим, что в случае жидкости постоянной вязкости П( x ) = р ( x ) и, следовательно, значение расходной толщины определяется максимальным входным градиентом контактного давления, а. значение минимальной толщины — минимальным выходным градиентом.

— соответственно (согласно [1]) минимальная толщина. смазочной плёнки и максимальное давление в слое жидкости постоянной вязкости, разделяющей жёсткий цилиндр и жёсткое полупрост- _h (IVR)                        _(IVR)

ранство (т. с. при Е^ = 0 , 153 V _о ^ 111 ар max ' = = 2 , 119 - 9 0= ^ 1, что соответствует режиму изо- V 0

вязкой смазки жестких тел (режим IVR) по классификации Джонсона. [5]).

В плоскости введенных параметров Q _о и V _о рассматриваемому случаю тяжело нагруженного гидродинамического контакта, цилиндра, и полупространства. соответствует подобласть, определяемая условием V _о ^ 1. Ив этой подобласти можно

выделить три характерные предельные (асимптотические) ситуации:

• 1)    вязкость смазочной жидкости практически постоянна внутри области упругогидродинамического (УГД) контакта — режим изовязкой смазки жестких тел с упругим покрытием (режим IVEC):

V о ^ 1 , Q о ^ 1;

• 2)    вязкость существенно увеличивается с ростом давления, но упругие свойства покрытия цилиндра проявляются до того, как «включится» зависимость (3) вязкости от давления:

V о ^ 1 , Q о ^ 1 , Q о р/^ ^ 1;

• 3)    зависимость вязкости от давления «включается» раньше, чем проявляются упругие свойства покрытия — режим пьезовязкой смазки жестких тел с упругим покрытием (режим PVEC):

V о <  1 , Q о V^ >  1 , Q 0 V о <  1 .

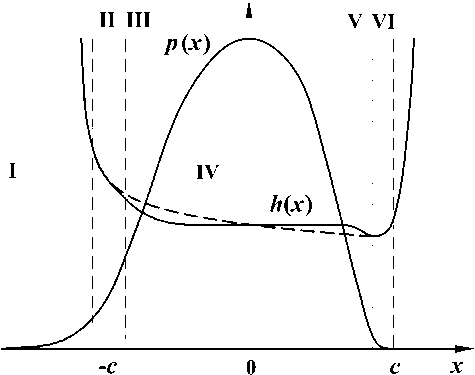
Рис. 3. Характерные участки области У ГД-контакта

Течение жидкости между цилиндром и основанием в каждом из указанных случаев естественным образом разбивается на ряд примыкающих друг к другу участков (см. рис. 3), имеющих собственные отличительные черты. Количество таких участков и особенности поведения давления и толщины смазочного слоя в них зависят от конкретной асимптотической ситуации. Но во всех случаях неизменно присутствуют два участка: а) центральный (несущий) участок. Его линейные размеры и распределение давления определяются условиями сухого контакта цилиндра с упругим покрытием и жесткого полупространства;

• б)    входной участок, на котором наблюдается без-расходное течение несжимаемой жидкости постоянной вязкости между жесткими телами заданной формы.

В предельном случае, определяемом условиями V 0 ^ 1 Q о ^ 1 (режим IVEC), кроме указанных двух можно выделить еще два участка. Это погранслои, окаймляющие центральный участок, внутри которых возникают (исчезают) эффекты, связанные с упругими свойствами покрытия, а уравнение Рейнольдса (1) «трансформируется» в уравнение сухого контакта (в главном приближении). При этом подачу смазочного материала в контакт можно считать обильной, если размеры входного участка значительно превосходят размеры входного погранслоя: |п| — c ^ V Vb*. Заметим также, что внутри погранслоев недефор-мированная поверхность цилиндра с достаточной точностью аппроксимируется наклонной пластиной — касательной к поверхности цилиндра, а течение жидкости на этих участках уже нельзя считать безрасходным. Форма смазочной пленки внутри центрального участка в главном приближении определяется градиентом давления, соответствующим сухому контакту цилиндра и полупространства, и в результате этого согласно [3] толщина пленки монотонно падает от 1 , 5 h _о до h min = 0 , 8491 h о- Причем значение расходной толщины слоя жидкости определяется максимальным входным градиентом контактного давления, а значение минимальной толщины — минимальным выходным градиентом, что полностью согласуется с комментариями к выражению (6). Входной (выходной) градиент контактного давления достигает своего максимума (минимума) на выходе из входного погранслоя (на входе в выходной погранс-лой) и в главном приближении максимальное (минимальное) значение входного (выходного) градиента давления находится из решения задачи о сухом контакте цилиндра с упругим покрытием и жёсткого основания.

В асимптотической ситуации Vо ^ 1, Qо ^ ^ 1, Qо VV0 ^ 1 дополнительно возникают еще два участка, отделяющие погранслои от центрального участка (см. рис. 3, пунктир соответствует предыдущему случаю Vо ^ 1, Qо ^ 1). В них «включается» и «выключается» зависимость (3) вязкости от давления. Толщина смазочного слоя внутри центрального участка постоянна и равна (экспоненциально близка) своему расходному значению hо. Расходное и минимальное значения толщины смазочной пленки в этой ситуации оказываются такими же, как и в предыдущем случае (Vо ^ 1, Qо ^ 1), то есть по-прежнему определяются соответственно максимальным входным и минимальным выходным градиентами давления, которые находятся из решения задачи о сухом контакте цилиндра и полупространства, и не зависят (в главном приближении) от пьезокоэффициента вязкости а. Входной градиент давления успевает достигнуть максимума прежде, чем становится заметным изменение вязкости, а выходной градиент достигает минимума уже после того, как норма- лизуется вязкость. Таким образом, асимптоти-ческуто ситуацию Vо ^ 1. Qо > 1. Qо yVO ^ 1 можно рассматривать совместно с ситуацией V0 ^ ^ 1, Qо ^ 1 как обобщенный режим изовязкой смазки жестких тел с упругим покрытием (обобщенный режим IVEC): V0 ^ 1, Q0VVQ ^ 1-

Наконец, в случае V о ^ 1, Q о VV 0 >  1 Q о V о ^ ^ 1 (режим PVEC) погранслои меняются местами с участками «включения» («выключения») зависимости (3) вязкости от давления (т. е. на. входе в УГД-коитакт рост вязкости смазочного материала. начинается раньше, чем успевают проявиться упругие свойства, покрытия цилиндра; на. выходе из контакта, наоборот, сначала, исчезают упругие деформации покрытия, а. потом приходит в норму вязкость). В этом случае подачу смазочного материала, в контакт можно считать обильной, если размеры входного участка, значительно превосходят размеры участка, «включения» зависимости (3) вязкости от давления: |а|—c > Q ₀ V ₀ b*. Следует также отметить, что при Q ₀y V o >  1 толщина, смазочного слоя внутри центрального участка, также постоянна, с большой степенью точностью и равна, (экспоненциально близка.) своему расходному значению h о, которое на этот раз определяется из интегрального соотношения

— c

• Q о V о У h—h ⁰ dx =1 ,

  -∞

где h — hо = x2 — c2- x < —c что соответствует форме входного зазора, вне сухого контакта. Минимальная толщина hmin смазочного слоя при этом определяется из другого интегрального соотношения h о

QV / --- о dh = — 1 , 2 c         h ³

• ^h min

h — h о « 2 c ( x — c ) , x < c.

Таким образом, в соответствии с соотношением (6) значение расходной толщины смазочного слоя зависит от того, успевают ли проявиться упругие свойства, покрытия цилиндра, или заметно измениться вязкость смазочной жидкости и в какой последовательности это произойдет прежде, чем входной (приведенный) градиент давления достигнет максимума. Искомая характеристика, контакта. — минимальная толщина, смазочной пленки h min — определяется минимальным выходным (приведенным) градиентом давления и для ее значения согласно [3] справедливы следующие приближенные выражения (возвращаемся к размерным переменным):

обобщенный режим обильной изовязкой смазки жестких тел с упругим покрытием ^обобщенный IVEC):

h ™ = 0 , 8941 h 0^IVEC) = 0 , 243Р^ 5 * при V о <  1. Q о V V q <  1- l^al — c >  V V q b*^:

режим обильной пьезовязкой смазки жестких тел с упругим покрытием (PVEC):

(PVEC) ^h min ⁼

(PVEC) h ₀

8* = Q о V о у * 8

при

V о « 1 , Q o pV o >>  1 , Q о V о « 1 , |н| — c > Q о V о b * .

Эти результаты согласуются с результатами В.П. Ковалёва. [6], решавшим аналогичную задачу асимптотическими методами, и результатами Д.С. Коднира [7], численно решавшим аналогичную задачу.

Видно, что в тяжело нагруженном гидродинамическом контакте ( V о ^ 1) цилиндра с упругим покрытием и жесткого полупространства, слой смазочной жидкости постоянной вязкости ( Q _о ^ ^ 1) оказывается существенно более толстым (режим IVEC), чем слой жидкости постоянной вязкости, разделяющий жёсткий цилиндр (без упругого покрытия) и жёсткое полупространство (режим IVR) при прочих равных условиях нагружения:

h mVR = 0 , 816 h о¹™) = 4 , 895 ^WR = 0 , 153 V о 5 * .

С другой стороны, смазочные материалы с большим пьезокоэффициентом вязкости (режим PVEC: Q _о V V q >  1- Q о V _о ^ 1) обеспечивают существенно большую толщину смазочной пленки, чем жидкости с постоянной вязкостью ( Q о ^ 1).

Для сравнения следует отметить, что в случае Vо ^ 1, QоVо > 1 минимальная толщина смазочного слоя hmin = 0, 816hо = 0, 252(QоVо)2/35* =

= 1 , 666[( ар ₀ u )² R ]1 / ³

не зависит от упругих свойств покрытия цилиндра, нагрузки, действующей на. пего, и имеет такое же значение, как и в случае качения жесткого

_h (IVR)

цилиндра. ( ™ = 0 , 153 V ₀ >  1) по тонкому слою вязкой несжимаемой жидкости с большим пьезокоэффициентом вязкости ( ар mVR) = 2 , 119 -% >

V 0

> 1), нанесенному на жесткое неподвижное основание (что соответствует режиму пьезовязкой смазки жестких тел (режим PVR) по классификации Джонсона. [5]). На самом деле, последнюю формулу можно применять, если одновременно выполнены два. условия (обобщенный режим пьезовязкой смазки жестких тел (обобщенный режим PVR)):

ар mVR =2 , 119 Q >>  1

V 0

и

(PVR)

• -min— = 0 , 252( Q о V о)² / ³ >  1 ,

δ∗ то есть если толщина слоя жидкости с большим пьезокоэффициентом вязкости существенно превышает упругие деформации поверхности цилиндра.

V. Выводы

Таким образом, в полном соответствии с классификацией Джонсона [5] можно выделить четыре асимптотических режима обильной смазки контакта цилиндра с упругим покрытием и жесткого полупространства:

• 1)    режим изовязкой смазки жестких тел (IVR): (IVR)

• -min- = 0 , 153 V о » 1 , δ_∗

ap mVR) = 2 , 119 % « 1 , |a| » q^ R- mVR ,

V 0

- mT) = 0 , 816 - <^IVR) = 4 , 895 ^WUR = 0 , 153 V о 5* ;

• 2)    обобщенный режим изовязкой смазки жестких тел с упругим покрытием (обобщенный IVEC):

V о « 1 ,  Q ор/^ « 1 ,   |п| — c » p/ V b b*,

- (mVEC = 0 , 8941 - l^IVEC> = 0 , 243/ V 0 5, ;

• 3)    режим пьезовязкой смазки жестких тел с упругим покрытием (PVEC):

V о « 1 , Q о /^ » 1 ,

Q о V о « 1 , lai— c » Q о V о b*,

- (PVEC) = - QPVEC) = ^Q о ^V о ⁵* . min =    2    =    8   ;

• 4)    обобщенный режим пъезовязкой смазки жестких тел (обобщенный PVR):

apmVR =2 , 119     » 1 ,

V 0

(PVR)

^— = 0 , 252( Q о V о)² / ³ » 1 ,

δ∗

I al» VW

• - mn^R) = 0 , 816 - о = 0 , 252( Q о V о )² / ³ 5* =

= 1 , 666[( ад _о u )² R ]1 / ³ .

Видно, что на режимах изовязкой смазки жестких тел без упругого покрытия (IVR) и жестких тел с упругим покрытием (обобщенный IVEC) безразмерная минимальная толщина смазочной пленки hmin определяется (в главном приближе-δ∗ нии) только лишь значением безразмерного параметра Vо. А на режимах пьезовязкой смазки жестких тел без упругого покрытия (обобщенный PVR) и жестких тел с упругим покрытием (PVEC) hm™ зависит (в главном приближении) от произведения безразмерных параметров Qо и Vо. Поэтому все четыре указанных режима могут быть наглядно представлены в виде схематической диаграммы (аналог диаграммы Джонсона [5]) в плоскости безразмерных параметров Vо и QоVо (см. рис. 4). На рис. 4 сплошные линии — линии уровня безразмерной минимальной толщины смазочной пленки hm^ для соответствующих асимптотических режимов смазки, пунктирные линии — интерполяция.

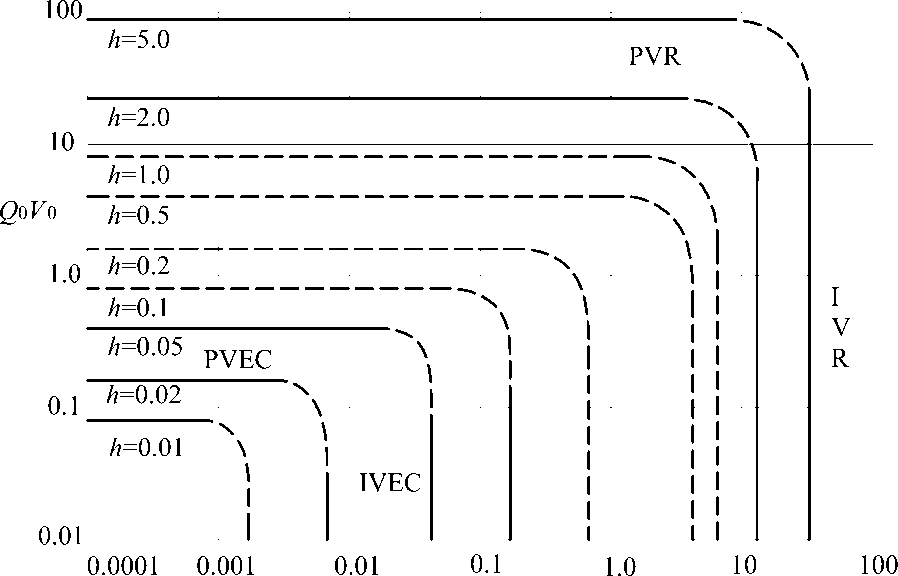
Го

Рис. 4. Линии уровня безразмерной минимальной толщины пленки