Асимптотические свойства предельных множеств Азарина

К С

А t

Пусть р (t) - некоторый уточнённый порядок. На пространстве определяется однопараметрическое семейство преобразований Азарина ^с ^ ^с, tе(0,да), согласно формулам рДЕ\ = pt = Atp,           '         ■

Для любого борелевского множества ^E .

Пусть ^ ^е Ф ¹ R о). Формула переменных даёт

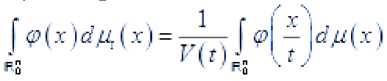
™-*х

< Г 6 К, : г = lim Л и. lim г

Пусть множество

предельным множеством Азарина и обозначим через

будем называть .

В случае вещественных радоновых мер наряду с предельным множеством Азарина Fr [ И ] важными асимптотическими характеристиками меры ^μ являются её верхняя конусная плотность и нижняя конусная плотность , а также верхняя плотность        и нижняя плотность

. Пусть – некоторое фиксированное число, – борелевское подмножество единичной сферы в пространстве ,                  .

Тогда указанные высшие величины определяются следующим образом

?

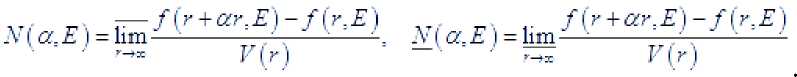
Заметим, что величины и

имеет смысл определить только в

случае, если уточнённый порядок

_  /^hm^(r)>0

таков, что

особенно наглядно для случая положительной меры. В случае

Это

Р >0

величины и не зависят от выбора числа

Заметим, что величины и не зависят от для любых уточнённых порядков . Эти величины имеют смысл рассматривать для любых уточнённых поряд-ков. Эти величины являются важными характеристиками мер, как в случае     , так и в случае     .

В общем случае, когда нет связи между мерой и уточнённым порядком каждая из четырёх величин является элементом расширенного множества вещественных чисел . Обычно величины , рассматривают как функции на пол-уоси . Однако, иногда удобно считать эти величины функциями на полуоси .

Из свойств пределов и уточнённого порядка ^{р ( r} ) вытекают следующие соотношения

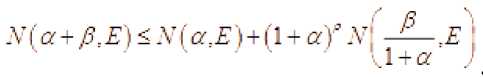
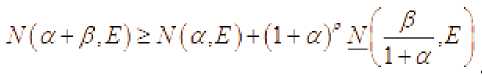
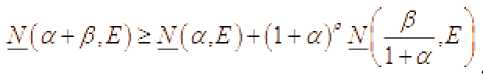
р = р ^ = lim р ( r ) где           r ^”

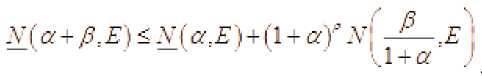
В общем случае функция

является не числовой

функцией, а фун-кцией со значениями из расширенной числовой прямой . Поэтому в неравенс-твах (3)-(6) правая часть не всегда имеет смысл. Если в каком-то из этих неравенств правая часть не имеет смысла, то соответствующее неравенство нужно считать пустым утверждением. По другому можно сказать так. Мы считаем, что неравенства        , выполняются для любого          .

Пусть мера μ положительна, то функция будет возрастающей. В этом случае из равенства (4) следует, что если конечна для

некоторого а >0, то она конечна для любого а >0. Отметим ещё, что для вещественных мер из неравенств (4), (6) следует, что если функция ограничена сверху на некотором интервале (0, ^), то она ограничена сверху на любом интервале (0 ,а), а если функция " : _ ограничена снизу на некотором интервале (0 ’^), то она ограничена снизу на любом интервале (0 ,а

Легко видеть, что для того, чтобы обе функции

и

были

непрерывными на полуоси выполнялись равенства

необходимо

и достаточно, чтобы

lim Ма,£) = 0

lim £(#,£) = О

Обозначим функцию

. Иногда мы будем рассматривать

А’ОЛ^И

-—/z((rsr + ar]x£j

= hm——--------

. (7)

Иногда возникает необходимость оценивать функцию с помощью

функций        и полезна функция

"   ~ . В этом случае наряду с функцией V ^{( r} ) = r P

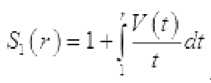
Как показывает опыт, применение функции ⁵ i ^{( r} ) становится неэффективным, если эта функция является ограниченной. В случае ограниченности функции ⁵ 1 ^{( r} ) применяют функцию

$2    | —— dt

С помощью правила Лопиталя получаем, что

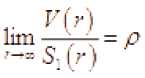
( ⁵ 1 ⁽ r ) — не ограничена)

Имеем

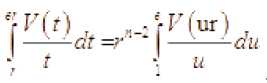
Поскольку

V ( ur )

V ( r ) ^ u^p

r -> то      u £ [ 1 , e ]

то

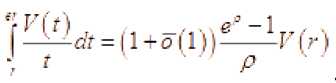
Из этого следует, что ^{V ( r} ) ^ ^{0 ( r} ^^{то )} , если ⁵ 1 ^{( r} ) - ограниченная функция.

Вновь применяя правило Лопиталя, получим lim

( ⁵ 1 ^{( r} ) - ограничена)

Из этих равенств видно, что функции ⁵ i ( r ) и ⁵ 2 ( ^r ) особенно важны в случае ■ “ ' " ^_ '. В этом случае функции ^s i ( ^r ) и ^ ^{( r} ) , а также функции ⁵ 2 ( ^r ) и ^ ^{( r} ) имеют различный рост на бесконечности.

Теорема 1. Пусть – произвольный уточнённый порядок, –

множество из единичной сферы, пусть ,    . Тогда, если при выполняется неравен-ство

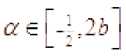
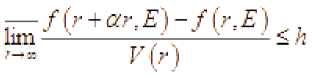
то равномерно на сегменте выполняется неравенство

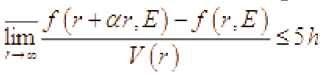
Последнее означает, что функция

7|/ + ^£)-/(л£)

Равномерно на сегменте стремится к нулю при

Доказательство. Обозначим            ,     ,       ,

. В новых обозначениях неравенство (4.13) выглядит так

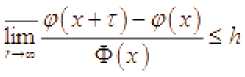
[-ln27h(U29

Если утверждение теоремы неверно, то существуют последовательность х„                  а а             El O.k(L-i)1 „ а                  а и посл-едовательность               такие, что выполняется неравенство

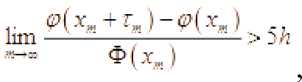
а = I O_rtnit’_| lr_2_rh’_ ("1 - 2^)—hl У i I

Пусть                        . Обозначим

£„ = [r5]:

t +

a )-y(x_t) < 2ЛФ(х^) Wc>m}

– возрастающая последовательность измеримых множеств. Из неравенства t°^l _   Ет™^=<>

• (4.14)    следует, что           . Поэтому            .

Далее обозначим

F„ = 7€[-4?_sln(l+ s)]: ^(x^ + rJ-^x^+rjt-/?) < 2^(x_t + r_t-/?) V£>m}

– также возрастающая последовательность измеримых множеств. Из

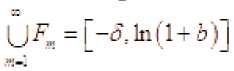
неравенства (12) следует, что

Поэтому

bm mesF„ = In (1 + b) + 5

Пусть

Обозначим

(арифметическая разность множеств).

Справедливы вклю-чения

Е, и являются частью сегмента

Сумма мер этих множеств больше длины указанного сегмента. Поэтому aeE;rF'       a = r пересечение этих множеств не пусто. Пусть        p . Тогда         , где

P^F,

. Поэтому выполняются неравенства

6>(x„ +й )~ ^(- k„ ) < 2ЛФ(х„)

, p (x„ + r„) - ф |xp + r, - /?) < 2ЛФ (x5 + г, - P ) .

оо               ,         х, + а = х„ + г„ -р

Складывая эти неравенства, и учитывая равенство               , получим

Обозначим . Далее находим

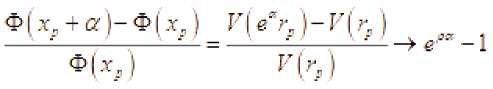
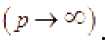
Так как а е (0;J , то при достаточно малых <5 и достаточно больших -:' будет х. + г.)—х.) < 5ЛФI х. J выполнять-ся неравенство                        . Это противоречит

• (4.15).    Теорема доказана.

Сейчас мы сформулируем условия, обеспечивающие существование предела

lim /z((r,2?]x£ j

. При выполнении этих условий функцииобозначены

одним символом

совпадают.

Теорема 2. Пусть pV? . такой уточнённый порядок, что функция ограничена. Пусть “ – мера Радона на полуоси IR₀ такая, что её функции №=£) ■A4ti)                       x                PM

,        , вычисленные относительно уточнённого порядка ограничены на некотором интервале (07d . Тогда для любого r- > 0

существует предел hni /z| (r.7?]x£ j

.

Доказательство. Из локальной ограниченности меры “ следует, что теорему доста-точно доказывать для случая r > 1 . В дальнейшем мы будем считать, что это неравенство выполнено.

Как уже отмечалось раньше ограниченность функций , на какомнибудь интервале (07d влечёт их ограниченность на любом интервале

I O.iz)                                                                                     ^)                        Т      . ^ J г

. Из этого, конечно, следует, что для любого величины

Х^-.Е1, конечны. Из доказательства лемм 4.3 и 4.4 легко усмотреть, что существует не зависящая от ^ величина м такая, что при г 5 1 выполняются неравенства

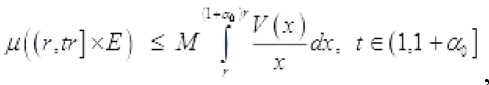
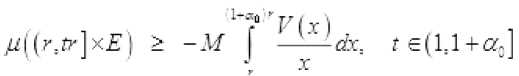
Из этих неравенств и ограниченности функции

■ ■ следует сходимость ряда

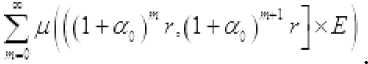
Из ограниченности функций ЕЧ.а.Е\ , ХАа-Е'\ на любом интервале '. 0_:с .1 следует их ограниченность на любом сегменте [с ₌ ^] "1-1^1. Тогда, как следует из теоремы 1, применённой к мерам “и А для любого » > 0 существует постоянная м такая, что для любых а е [0_:6] и любого г 5 1

выполняется неравенство

.

Мы уже отмечали, что из ограниченности функции S. । г । следует, что 7 (г) ^ 0 (> ^ =С') .