Асимптотический анализ двухкритериальной модели реальных инвестиций на основе Z-преобразования

В данной работе рассматривается задача, обобщаю- тие имеет капитал K0 . При этом государственный орган щая задачу из работы [1] на случай двух критериев, ко- (ГО) для реализации инвестиционного проекта (ИП) торую сформулируем следующим образом. Предприя- выделяет инвестиции не более величины I0 на приоб- ретение активных основных производственных фондов (ОПФ) n видов. Необходимо определить стоимость (количество) всех приобретаемых в моменты t = 1, _., T ОПФ каждого вида, при которых дисконтированные суммы собственных средств предприятия и его налоговых поступлений в ГО максимальны за все время действия ИП. При этом выполнены следующие основные предпосылки:

• 1)    учитываются налоги, составляющие большую часть затрат предприятия: налог на добавленную стоимость (НДС), налог на прибыль (НП), налог на имущество (НИ), единый социальный налог (ЕСН) и отчисления в фонд оплаты труда (ФОТ);

• 2)    предприятие имеет достаточные запасы сырья;

• 3)    срок T действия ИП меньше сроков T_k службы единицы ОПФ каждого типа: T <  T k ( к = 1,..., n );

• 4)    на ОПФ каждого вида производится лишь один тип продукции. С учетом приведенных предпосылок сформулированная выше задача имеет вид двухкритериальной многошаговой задачи линейного программирования (МЗЛП), которую, согласно работе [2], назовем моделью B 1:

x k ⁽ t + 1) = x k ⁽ t ) + u k ⁽ t )

( к = 1,..., n ; t = 0,..., T - 1),

n

X n +1 ( t + 1) = - S X k ( t ) / T k + X n +1 ( t ) + к =1 n

+ S U k ( t ) ( t = 0,..., T - 1)

k =1

xn+2 (t + D = -a2 xn+1 (t) + xn+2 (t) - n

• - S u k ⁽ t ) ⁺ u 2 n +1⁽ t ) ⁺ u 2 n +2⁽ t ) ⁽ t = ⁰⁾ ,            ⁽¹⁾

k =1

nL X. ( t )

xn+2 (t + D = a3 S --6xn+1 (t) + xn+2 (t ) - k=1 Tk nn

• - S uk ⁽ t ) ⁺ y S u n + k ⁽ t ) ⁽ t = U-, T ^- 1);

k =1                k =1

X k (0) = 0( k = 1,..., n + 2);

X n +2 ( t ) >  0 ( t = 1,..., T ), ^Xk ⁽ t )             , X

S v    a 2 Xn+1 (t)+ k=1   Tk

+ (1 - р£> „ + k ( t ) > 0 ( t = 1,..., t - 1);

k =1

U n + k ( t ) <  s k X k ( t ) ( k = 1,..., n ; t = 1,..., t - 1),

^U 2 n +1 ⁽⁰⁾ <  I 0 , ^U 2 n +2 ⁽⁰⁾ <  K 0 , u_k ( t ) > 0 ( k = 1,..., n ; t = 0,..., T - 1), U n + k ( t ) >  0 ( k = 1,..., n ; t = 1,..., T - 1),

U 2 n +1 (0) >  0, u 2 n +2 (0) >  0,

J = { J 1 , J ₂} ^ max , где J 1 =^- u 2 n +1^{(0) - u} 2 n +2^{(0) +}

T -1 S t =1

^a 3 S ^^ ^{- 6 X}n +1 ⁽ t ) ⁺ y S u n + k ⁽ t )

k =1 T k _____________________ k =1 __________ J +

(1 + r ) t

5 Xn +1 ( T )

(1 + r ) ^{T -1} ’

T - 1

J2 =S t = T2

- Из] n: x Д^{( t )} + 6 X i( t ) + PlLU n + k ( t ) k = 1 T k           n ^{+ 1}            k = 1

(1 + Г ) t соот-

ветственно дисконтированная сумма собственных средств предприятия и налоговых поступлений в ГО; Uk(t)(t = 0,..., T -1), Un+k(t) (k = 1,..., n; t = 1,..., T -1), u2n+1(0) и u2n+2(0) - стоимость приобретаемых ОПФ, вы- ручка от реализации продукции k -го типа, внешние и внутренние инвестиции соответственно; Xk(t) (k = 1,..., n), Xn+1 (t), Xn+2( t) (t = 0,..., T) - соответственно накопленная стоимость всех ОПФ k-го типа, остаточная стоимость всех ОПФ, текущие денежные средства предприятия в момент t; Vk, Tk, ck и Pk - соответственно производительность, срок службы, стоимость единицы ОПФ и стоимость единицы продукции k-го типа; 10, K0 - суммы внешних и внутренних инвестиций, выделяемых на весь срок действия ИП; а1, а2, а3, а4 - ставки НДС, НИ, НП и ЕСН соответственно (НДС включается в цену продукции, поэтому можно считать, что а, = 0); Р - доля выручки от реализации, выделяемая на ФОТ; 6 = (1 - а3)а2, 5 k = PkVk / ck (k = 1,..., n), Y = (1 - а3)(1 - в), p = (1 - в)а3 + а4в, r - ставка доходности ИП; 5 (0 < 5 < 1) - доля остаточной стоимости всех ОПФ на момент t = T от ее балансовой стоимости, определяемая в общем случае экспертно.

Согласно исследованию [3], многокритериальная МЗЛП (ММЗЛП) (1), (2) равносильна однокритериальной задаче с условиями (1) и максимизацией свертки критериев J (р) = р 1 J 1 + p₂ J ₂, где p е M = {(р 1 ; р₂) е E ²1 р i >  0 ( i = 1, 2); р 1 + р₂ = 1} - вектор параметров, E ² - двумерное евклидово пространство. Поскольку р₂ = 1 - р 1 , то, обозначая р = р 1 , перейдем от ММЗЛП (1), (2) к эквивалентной ей однокритериальной задаче (1) при следующем условии:

J (р) = p J 1 + (1 - р) J ₂ ^ max (р е (0;1)). (3)

Для задачи (1), (3) имеет место лемма [2], аналогичная лемме из публикации [1].

Лемма. Для оптимальных значений переменных U n _{+ k} ( t ) и X k ( t )( k = 1,..., n ; t = 1,..., T - 1) модели (1), (3) справедливо равенство

U n + k ( t ) = 5 k X k ( t )( k = 1,..., n ; t = 1,..., T - 1). (4)

Здесь и далее * обозначены оптимальные значения переменных и критериев. Условие (4) означает следующее: в оптимуме выручка от реализации в модели (1), (3) (а значит, и в задаче (1), (2)) равна стоимости произведенной по каждому виду продукции.

Рассмотрим задачу двухкритериальной оценки ИП, описанного моделью (1), (2), когда продажа ОПФ предприятием не предполагается, т. е. 5 = 0. Для применения z -преобразования к анализу модели (1), (3), доопределим управления, U_k ( t )( k = 2 n + 1,2 n + 2; t = 1,..., T - 1) до вектора постоянной размерности n + 2 (поскольку переменные U_{n + k} ( t ) ( k = 1,..., n ; t = 1,..., T - 1) можно исключить согласно (4)), полагая отсутствующие переменные равными нулю, т. е. дополняя указанную задачу условиями ^U 2 n +1 ⁽ t ) < 0 , ^U 2 n +1 ⁽ t ) >  ⁰ ; ^U 2 n +2 ⁽ t ) <  ⁰ , u _{2 n + 2} ( t ) >  0 ( t = 1,..., T - 1). Учитывая (4) и начальные условия, запишем ее ограничения и критерии единообразно, перейдя к МЗЛП:

x_k ⁽ t ⁺ 1) = x k ⁽ t ) ⁺ u k ⁽ t )

(k = 1,..., n; t = 0,..., T-1), xn+1 (t + D = -S xk (t) / Tk + xn+1 (t) + k=1

+ £X( t ) ( t = 0,..., T - 1)

k =1

x n +2 ⁽ t ^{+ 1)} = S Y k x k ⁽ t ) ^- 9 x n +1 ⁽ t ) ⁺ x n +2 ⁽ t ) ^- k =1

- S U ⁽ t ) ⁺ u 2 n +1 ⁽ t ) ⁺ u 2 n +2 ⁽ t ) ⁽ t = ⁰ — ^{T - 1)} ;

X k (0) = 0 ( k = 1,..., n + 2);               (5)

X n +2 ( t + 1) >  0 ( t = 0,..., T - 1),

S о k X k ( t ) - a 2 X n +1 ( t ) > 0 ( t = 0,..., T - 1), k =1

U 2 n +1 ( t ) <  1 0 , U 2 n +2 ( t ) <  K a ( t = 0);

U 2 n+1( t) < 0, U 2 n+2 ( t) < 0( t = 1,..., T-1), uk(t) > 0 (k = 1,..., n; 2n +1, 2n + 2; t = 0,..., T -1);

J(ц) = ц J1 + (1 - ц) J2 > max (ц e (0; 1)), где

_    T -1

J1 =S t=0

n

S Y k x k ⁽ t ) ^{- 9} x n +1 ⁽ t ) ^{- U} 2 n +1 ⁽ t ) ^{- U} 2 n +2 ⁽ t )

_ k =1

(1 + r ) t

_    T -1

J 2 = S t=0

n

S to k x k ⁽ t ) + ⁹ x n +1⁽ t )

. k =1

Y k = ^аз / ^Tk ⁺ Y ⁵ k ;

^{( 1 +} r ) t

to k = - а з / T k + p5 k ; о k = (1 - P)5 k - 1/ T k ( k = 1^..., n ). По построению для целевых критериев J (ц) и J (ц) соответственно задач (1), (3) и (5) имеет место неравенство: J (ц) <  J (ц). В частности,

*

J *(ц) <  J (ц)(ц e (0;1)). (6)

Полагая z = 1 + r > 1, перейдем в задаче (5) к пределу при T ^да . В силу предпосылки (3), T ^ +да fi T_k ^ +да , откуда следует, что y _k ^ Y^ _k , to _k ^ p6 _k , о _k ^ (1 - в)3 _k ( k = 1,..., n ). Применяя к последней МЗЛП z -преобразование и учитывая формулу Z ( x ( t + 1)) = z [ X ( z ) - x (0) ] , получим двухпараметрическую (по параметрам ц и z ) статическую задачу линейного программирования (ЗЛП):

zX_k ( z ) = X k ( z ) + U_k ( z )( k = 1,..., n ),

n zXn+1( z) = Xn+1( z) + S Uk (z), k=1

n zXn+2( z) = yS 5 kXk (z) - 9Xn+1( z) + k=1

n

+ X n +2 ( z ) - S U k ( z ) + U 2 n +1 ( z ) + U 2 n +2 ( z ) , k =1

zX n +2 ( z ) >  0,

(1 - e) S 5 k X k ( z ) - a 2 X n +1 ( z ) >  0,         (7)

k =1

U 2 n +1 ( z ) <  1 0 , U 2 n +2 ( z ) <  K 0 ;

U_k ( z ) >  0 ( k = 1,..., n ;2 n + 1,2 n + 2);

J (ц, z ) = ц J 1 ( z ) + (1 - ц) J 2 ( z ) ^ max (ц e (0;1); z >  1),

n где J 1(z) = yS 5kXk (z) - 9Xn+1 (z) - U2n+1 (z) - U2n+2 (z) , k=1

n

J 2( z) = pS 5 kXk (z) + 9Xn+1( z), k=1

Uj(z) = j^Uj(t)z-t (j = 1,..., n;2n +1,2n + 2)             и t = 0 да

X_k ( z ) = S x k ( t ) z - t ( k = 1,..., n + 2) - z -изображения уп- t =0

равляющих_и фазовых переменных задачи (5), J (ц, z ) = T im J (ц), причем при T ^ +да по построению J * (ц) <  J * (ц, z ) (ц e (0; 1)), откуда в силу выражения (6) получим

*

J (ц) <  J (ц, z )(ц e (0;1); z >  1).          (8)

Выражая из уравнений в ЗЛП (7) переменные X_k ( z ) ( k = 1,..., n + 2), имеем

X k ( z ) = Uk^z ) ( k = 1,..., n ), z - 1

n

S U k ( z )

Xn+1( z) =            - z -1

X n +2 ( z ) =

n

S (y5 k - 9 - z + 1) U k ( z ) + ( z - 1)( U 2 n +1 ( z ) + U 2 n +2 ( z ))

_ k =1 ________________________________________________________________ ( z - 1)²                                .

Подставляя последние формулы в оставшиеся выражения указанной задачи и учитывая, что z = 1 + r >  1, запишем параметрическую статическую задачу, совпадающую с приведенной в работе [2] и эквивалентную модели ZB 1:

n

S (9 + r - y5 k )U_k ( z ) - r(U 2 n +1 ( z ) + U 2 n +2 ( z )) <  0, k =1

n

S (9 - y5 k )U_k ( z ) <  0, k =1

U 2 n +1 ( z ) <  1 0 , U 2 n +2 ( z ) <  K 0 ,

U_k ( z ) >  0( k = 1,..., n ;2 n + 1,2 n + 2),         (9)

J ⁽ ц, z ) = ¹ S Ф k^Uk ⁽ z ) ^- Ц ^{[ U} 2 n +1⁽ z ) + r k ■

^{+ U} 2 n +2⁽ z ^)] ^ ^тах( ц ^e (0; ¹ ))

где ф _k = [1 - 2ц]9 + [цY + (1 - ц)р]5 _k ( k = 1,..., n ; ц e (0; 1)).

Заметим, что в указанной работе ММЗЛП (1), (2) получена формально из более общей модели A , отличающейся от нее дополнительным ограничением

Un+k (t) < qk (t +1) (k = 1,..., n; t = T 2,._ T-1), (10) при условиях qk(t+1) >+ /

( k = 1,..., n ; t = T ²,._ T - 1);                (11)

T ¹ = T ² = 1.

Здесь q_k ( t + 1) ( k = 1,..., n ; t = T², ..., T - 1) - прогнозный спрос на продукцию k -го типа в момент t + 1, T ¹ и T ² - моменты окончания инвестирования и начала производства. При этом, согласно работе [2], в модели ZA , полученной после применения z -оператора к задаче А , появляются агрегированные ограничения

U n ₊ к ( z ) < Q k ( z ), U_n + к ( z ) <^a U ¹ z ¹ ( к = 1,..., n ), (12) z - 1

def ”'

где Q_k ( z ) = ^ q_k ( t + 1) z ^t ( к = 1,..., n ). Первое из них в t = T¹

силу условия (11) примет вид U_{n + к} ( z ) < +да ( к = 1,..., n ), и исключается как избыточное, а второе, являющееся единственным ограничением на переменные U_{n + к} ( z ) ( к = 1,..., n ; z >  1) сверху, в оптимуме выполняется как равенство, поскольку целевая функция в ZA максимизируется, а ее коэффициенты при указанных переменных положительны:

С к ( z ) = "^ 'z ' ( к = 1,..., n ). z -1

Указанное выше совпадение ЗЛП (9) с задачей из монографии [2] подтверждает правильность выводов, полученных в отмеченной работе формальным многократным предельным переходом согласно 1-го из условий (11). При этом рассмотренный выше подход является более строгим (поскольку не использует указанного предельного перехода, а значит, не требует обоснования его правомерности). Отметим, что, если не учитывать «динамические» соотношения (4) (достаточно рутинное доказательство которых приведено в том же источнике), то получим ЗЛП, в которой, в отличие от задачи ZA , отсутствует 1-е из неравенств (12). Учитывая «статические» равенства (13), вновь получим ЗЛП (9). Авторская методика из указанной монографии [2] может рассматриваться в качестве правдоподобных и простых наводящих рассуждений (требующих последующего обоснования), позволяющих трактовать задачи (1), (2) и (9) как частные предельные случаи при условиях (11) моделей A и ZA соответственно. Решение z -задачи (9), найденное там же, определяется следующей теоремой.

Теорема 1. Если найдется такой номер к ₀ е {1,..., n }, что б _к = max б _к , причем — <  б. <  ^{6 +} r , то в ЗЛП (9)

0 к=1,..., n                        Y 0 Y существует нетривиальное решение

U k о ( z ) = r ( I о + K о )/(6 + r - Y6 к о );

U n + к о ( z ) = б к о ( I о + K о )/(6 + r - y8 к о ),

U k ( z ) = о; U n + к ( z ) = о( к = 1,..., n ; к # к о );

U 2 n + 1 ( z ) = I о , U 2 n + 1 ( z ) = K о , которому в пространстве критериев соответствует единств енная ненулевая Парето-точка с координатами =*      ( 2уб - 26 - r )          =•      ( 6+рб^ )

J ( z ) = I --------l [ I_o + K ]; J ₂ ( z ) = I---- ^k-2— l [ I_o + K ]

IV/                              со о 2                                Н~о о

I 6 + r - y6l l                      I 6 + r - y6l l

V             kо J                         V            k о J для всех значений ц, задаваемых соотношениями "б к о > (26 + r )/(2y), ц е (о;1)

б^ < (26 + r) / (2y), ц е (о; (6 + рб^ )/[36 + r + (р - 2y)6ц ]). о                                                                        о

При этом оптимальное значение свертки J (ц, z )

в

указанной

ЗЛП

равно

=*

J ⁽ ц, ^z ) =

U21 , (z) = Uk(z); U t (z) = Un+к(z) (к = 1,..., n); 1 k I1

V1(z) = U2n+1(z); Vг(z) = U2n+1(z)(14)

и переходя формально к пределу при n ^ да , переформулируем указанную теорему в следующем виде.

Теорема 2. Если б, = max б_к таково, что к =1,...

⁶ . ^{6 + r}

- < ^б1 <----- ,                   ⁽¹⁵⁾

γγ то в ЗЛП (9) даже при неограниченном количестве видов продукции существует нетривиальное решение

U ( z ) = r ( I о + K о )/(6 + r - y6 1 );

Ц ; ( z ) = б 1 ( I о + K о )/(6 + r - y6 1 );

U k ( z ) = о( к = 3,...);

V( z) = Iо, Vi( z) = Kо, которому в пространстве критериев соответствует единственная ненулевая Парето-точка с координатами

_ *

J 1 ( z ) =

2y6 1 - 26 - r )

—----J— l^[ I о ⁺ K о^] ;

6 + r - y6₁ J

_ *

J 2 ( z ) =

6+рб 1

6 + r - y6₁

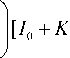
для всех значений ц , задаваемых соотношениями "8 1 > (26 + r )/(2у), ц е (о;1)

8 1 < (26 + r ) / (2у), ц е (о; (6 + рб 1 )/[36 + r + (р - 2у)б 1 ]).

=*

При этом предел оптимального значения свертки J (ц, z ) в         указанной         задаче         равен

= *.    . (6+рб, + [<2у-р)б, -36 -r]ц 1, lim J (ц, z) = I —t-1---1---------H l[Iо + Kо]. n^”           V         6 + r - уб1          J

Справедливы следующие теоремы, доказательство которых также приведено в монографии [2].

Теорема 3. В ЗЛП вида f (x) = (c, x) ^ max;

n gj(x) = Zajixi + aj < о(j =1’-,k)       (17)

i =1

решение существует тогда и только тогда, когда множество X , задаваемое ее ограничениями, не пусто и функция f ( x ) ограничена сверху на этом множестве.

Теорема 4. Оптимальное значение свертки J * (ц) в проекте, описываемом моделью A , есть неубывающая функция от параметров T , n , T ¹ , Y, б; б к , q k ( t ) ( к е {1,..., n }; t е { T ² + 1,..., T }); I о , K о и невозрастающая от T ² ,6 и r (T , n , T 1 , T ² е {1, 2,...}) при неизменных значениях остальных параметров и ц е [ о;1 ] .

Отметим, что доказательство теоремы 3, предложенное в работе [2], не использует конечность числа переменных и ограничений задачи (17), задающих множество X . Поэтому данная теорема выполняется и в том случае, когда число переменных и/или неравенств бесконечно, т. е. полагаем в частности, что в указанной задаче n ^ да и/или к ^ да . _, _*

Поскольку J (ц, z ) = J (ц, z ) (ц е (о;1); z >  1), то при n ^ да из теоремы 2 и неравенства (8) получим условие, аналогичное следствию 3.5.1 из работы [2] для конечного n :

lim lim J * (ц) <

T ^m n ^«

6 + р5 , + [(2y - р)5 .

6 + r - y^_x

³⁶ r ^]Ц I [ 1 0 + K 0 ],(18)

из которого следует, что при условиях (15) и неограниченных n , T целевая функция J (ц) (ц е (0; 1)) МЗЛП (1), (3) ограничена сверху. Поскольку управление (полученное перенумерацией исходных пер еме нных указанной задачи, со-

J_i | _A , J_i ( z )| _ZA – значения i -го критерия в Парето-точке задач A и ZA соответственно, из которого в силу (16) следует, что даже при условиях теоремы 5 (следствия) координаты Парето-точек критериального пространства задачи A ограничены сверху:

J ,4 <

о тве тствующей заменам (14)) u

2 к - 1

u _M ,( t ) = 0( к = 1,...; t = 1,...);

2 кI v2 n+2( t) = 0( t = 0)     является

( t ) = 0( к = 1,...; t = 0,...);

v 2 n +i ( t ) = 0( t = 0), допустимым   при

J * L <

2y61-26 - r 1

6 + r - y6 , J¹ 1 ^{0 +} K ⁰] ^;

.( ^p I [ + ]

( 6 + r - y61 )

T ^ m; n ^ m , а задачи (1), (2) и (1), (3) эквивалентны, то по теореме 3 доказали следующую теорему.

Теорема 5. Если 6₁ = max 6 _к удовлетворяет условиям ^к = ^1, ...

(15), то в ММЗЛП (1), (2) даже при неограниченном количестве видов продукции на бесконечном временном интервале существует нетривиальное решение, причем имеет место неравенство (18).

Для содержательной корректности предельного перехода при n ^ м в теореме 2 номер к ₀ е {1,..., n } должен перенумеровываться так, чтобы он не зависел от n .

При условиях (11) из теоремы 4 и теоремы Вейершт-расса о существовании предела ограниченной монотонной последовательности следует справедливость теоремы 5 и для модели A с конечным спросом и на конечном интервале времени. Более того, принимая во внимание, что предложенный в этой работе подход строго обосновывает правомерность предельного перехода согласно 1-го из условий (11) и получаемых с его помощью результатов, а значит, позволяет с формальной и экономической точки зрения интрепретировать модели B 1 и ZB 1 как частные асимптотические варианты моделей A и ZA соответственно при указанных условиях, из теоремы 5 получим следствие, являющееся по сути ее переформулировкой.

Следствие. Если 6₁ = max 6 _к удовлетворяет условиям (15), то в задаче А даже пр инеограниченном количестве видов продукции и неограниченном спросе в каждый момент времени в период производства и по каждому виду на бесконечном временном интервале существует нетривиальное решение, причем имеет место неравенство (18).

Заметим, что теорема 5 (или следствие) носит содержательно парадоксальный характер: хотя основные экономические характеристики ИП, описываемого моделью B 1 (или A ) – число различных видов ОПФ, горизонт планирования (и спрос на продукцию) бесконечны, значение свертки ее критериев, соответствующее Парето-точке критериального пространства, является конечным при условиях (15) и любых значениях остальных параметров проекта. Согласно численных экспериментов, представленных в главе 2 работы [2], справедливо эмпирическое соотношение J * | . <  J * (z ) | ZA ( i = 1,2; ц е (0;1)), где

Этот же факт можно обосновать строго от противного, учитывая, что ц е (0; 1), вид свертки в (3) и условие (18). Содержательно указанный результат объясняется тем, что если максимальная фондоотдача ОПФ каждого вида (характеризующая их экономическую эффективность) заключена в диапазоне (15), то при условиях теоремы 5 (следствия) в проекте оптимизации реальных инвестиций предприятия, описываемом моделью B 1 ( A ), даже в оптимуме целевые критерии ограничены сверху.

Отметим, что если не делать замен (14), то теорему 5 сложно интерпретировать полностью содержательно. Аналогично можно показать, что если в модели A отсутствует ограничение (1 0) для некоторого

к е {1,..., n }; t е { T 2 ,

..

., T - 1}, то в соответствующей z -за-

даче отсутствует 1-е из ограничений (12) для указанного номера k , что формально можно получить из упомянутого ограничения при q k ( t ) ^ +м , т. е. при Q k ( z ) ^ +м .

На основе z-преобразования можно дать более простой метод доказательства леммы. Допустим, что существуют к е {1,..., n }; t е {1,..., T - 1}, при которых равенство (4) в оптимуме не выполняется, т е. u n_{+ к} ( t ) <  6 _kx*_k ( t ). Поскольку в ЗЛП оптимум достигается на границе допустимого множества, то последнее неравенство можно исключить, поскольку оно является строгим. Тогда, аналогично предыдущему замечанию, 2-е из условий (12) отсутствует, что противоречит (13), а значит, указанное строгое неравенство невозможно, откуда следует (4).