Асимптотический метод расчета поля от оптических элементов, обладающих зонной структурой

Рассмотрим дифракцию света на дифракционном оптическом элементе (ДОЭ), обладающем зонной структурой. Свет представляет собой электромагнитные волны, и поэтому строгое решение задачи дифракции должно быть основано на решении системы уравнений Максвелла с соответствующими задаче граничными условиями. Однако на практике хорошо известно, что решение уравнений Максвелла в коротковолновой области весьма трудоемкая задача даже для современных компьютеров. Для оценки поведения решения системы уравнений Максвелла в коротковолновой области широко используются асимптотические методы. Наиболее известным асимптотическим методом является приближение геометрической оптики [1]. Приближение геометрической оптики хорошо работает в случае, когда свойства среды слабо меняются на расстояниях сравнимых с длиной волны освещающего пучка. Методы решения задач дифракции на периодических структурах, основанные на точном решении уравнений Максвелла, хорошо известны [2]. Если структура не является периодической, то для решения задач дифракции используются конечно-разностные методы [3] или методы, основанные на решении соответствующих интегральных уравнений [4]. В работах [5-7] рассмотрены асимптотические методы решения волновых уравнений для решения задач дифракции в рамках скалярной теории. В работе [8] представлены методы расчета поля от спиральной фазовой пластинки в рамках параксиальной векторной теории. В работе [9] разработаны методы решения задач дифракции на микрочастицах.

В данной работе рассматривается асимптотический подход к решению широкого класса задач дифракции в рамках электромагнитной теории. Подход основан на синтезе асимптотического метода к расчету поля после ДОЭ, основанного на вычислении интеграла Кирхгофа-Котлера методом стационарной фазы, и решения задач дифракции на квази-периодических структурах внутри ДОЭ. Полученные с использованием данного метода формулы для поля от ДОЭ можно легко интерпретировать в рамках геометрической оптики.

Применение асимптотических методов в физике связано в основном с использованием геометрической оптики [1], квазиклассического приближения в квантовой механике, а также с вычислением интеграла Кирхгофа-Гюйгенса [10] или Кирхгофа-Котлера [11] методом стационарной фазы или методом перевала. Физический смысл подхода в геометрической оптике состоит в замене решения исходной задачи на решение задачи дифракции локальной плоской волны в локально однородной среде или на плоской границе раздела двух сред. Метод перевала и метод стационарной фазы [10-12] также основаны на замене вычисляемого интеграла некоторым эталонным интегралом. Эти методы были положены в основу результатов, изложенных нами в работах [5-7] в рамках скалярной теории дифракции. В настоящей статье предложенный в [5-7] подход обобщен на случай строгой электромагнитной теории.

1. Теория представлений для уравнений Максвелла

В данной работе расчет поля проводится в рамках строгой векторной электромагнитной теории. В декартовой системе координат систему уравнений Максвелла [13] для гармонических по времени полей можно представить в виде i d W k0 dx3

= HW ,

где Н – матричный дифференциальный оператор Гамильтона-Максвелла,

W ( X ) =

E 1

E 2

H 1

, 2п к = — 0 X

1 в = —г

2 к 0 ² L

д / д х 1 д / д х ₂

д / д х 1 -д / д х 1 д / д х 1

д / д х ₂ -д / д х ₂ д / д х ₂

H 2

X = ( х 1 , х ₂, х 3 ) - декартовы координаты, X - длина волны, E i – поперечные компоненты электрического поля, H i – компоненты магнитного поля.

Для описания электромагнитного поля в случае гармонического изменения поля по времени достаточно четырех компонент электромагнитного поля. Продольные компоненты электрического (и магнитного) поля в случае необходимости можно выразить через поперечные. Представление системы уравнений Максвелла в виде (1) удобно для решения задач дифракции, в которых описывается распространение электромагнитных волн через объекты, имеющие границы в форме параллельных плоскостей. Этим свойством обладают, например, элементы плоской оптики, работающие в оптическом диапазоне.

В дальнейшем четырехкомпонентный вектор W будем называть бивектором, а соответствующее поле – бивекторным электромагнитным полем.

В данной работе используются введенные П. Дираком [14] обозначения для полевых функций, принятые в квантовой механике, в т.ч. 5 -функции. При этом одни и те же символы с разной индексацией могут иметь разный смысл.

Выражение (1) можно рассматривать как операторную запись в абстрактном гильбертовом пространстве бивекторов. В координатном представлении оператор Гамильтона-Максвелла Н имеет следующий вид:

B

A

- 1 д / д х 1

2 к ₀ ² д / д х ₂

д / д х 1 s ¹    0

д / д х ₂ 0 s ^{- 1}

х

-д / д х 1

-д / д х ₂

д / д х 1     0 1

д / д х ₂ Д- ¹ 0

^а3^а1 W J Г*    ^а 2 (| | W J| Vs)

| F ) =  ^а3^а2 W JГ*   ^-а1 (I W h II V^s)

^-а2 Vs| W J I"'     ^аз^а1 || W_A | I"'

, « 1 ViH W JГ'     ^аз^а2 || W_A |Г’

где к = к 0Vs, || W_e ||² = ( а2 +s )( а² +а³₂ ) ,

II Wh\ |² = ( ^а 32 ^+s - 1 )( ^а 2 ^+а 2 ) ,

а ₃ = V1 - ( а 1 ) 2 - ( а ₂ ) ² .

s

0 1Г 0

s 1

- 1

где s - диэлектрическая проницаемость среды, ц = 1.

Представим решение уравнения Максвелла в виде разложения по базису

| W ) = I f nms ( х 3 )| F nms ( х 1 , х 2 )) .                   (5)

nms

Набор функций { f ^nms ( х ₃ ) } будем называть волновыми функциями бивекторного электромагнитного поля в F -представлении. nms - набор индексов, характеризующий базисную функцию.

Каждому абстрактному оператору Н в данном базисе можно сопоставить многомерную матрицу (или тензор [15]) H_n ^p _m ^q _s ^l

H I F nms ( х 1 , х 2 )) = I Н £ ( f ) | I   ( х 1 , х 2 )) .     (6)

nms

В случае, когда набор базисных функций не является счетным, суммирование заменяется интегрированием. Система уравнений Максвелла в F -представлении записывается в виде:

nms т f = I НП (х3) fpql (х3).                (7)

^{к д х} 3      pqi

Выберем в качестве системы линейно независимых решений набор функций, представляющих собой плоские волны. В этом случае решение представляется в виде:

да да

IW) = ЕП f “1“2z (х3 )| F.^s (х1, х2)) d«1 d«2, (8) s -да -да где а1,а2 - пространственные частоты.

Базисные векторы запишем в виде матрицы

| ^F a 1 a ₂ ( ^х 1 , ^х 2 )) = | ^F a 1 a ₂ )' exP ( ^Тк ( ^а 1 ^х 1 + ^а 2 ^х 2 ) ) ,     ⁽⁹⁾

^-а 3 ^а 1 | W J Г’    ^а 2 (| I W JI Vs)

• ^-а 3 ^а 2 H W J Г’ - ^а 1 (I W JI Vs )

• ^-а2 VI | W J Г'    ^-а3^а1 | W_A | I"'

U 1 vs I W IГ¹      -а 3 а 2 | W₆ |Г¹ ,

Первый столбец матрицы описывает ТЕ-волну с пространственными частотами ю 1 , ® ₂, распространяющуюся в положительном направлении. Второй столбец описывает ТМ-волну с пространственными частотами ю 1 , ® ₂, распространяющуюся в положительном направлении. Третий столбец описывает ТЕ-волну с пространственными частотами ю 1 , ® ₂,

распространяющуюся в отрицательном направлении. Четвертый столбец описывает ТМ-волну с пространственными частотами © 1 , © 2 , распространяющуюся в отрицательном направлении. В предельном случае, когда а , = a ₂ = 0, будем использовать мат-

рицу следующего вида:

-1

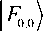
Vs +1

-Vs

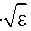
1      0 '

0     1

0 Vs

—Vs 07

	Г a1a3      a2         0         0   ^
	II W 1II vsi| W 2||
	a 2 a 3      —a 1       A        A
V,„ =	II W 1II vsi| W 2||	. (18)
	0       0      —a 2 Vs  —a 1 a 3
	II W 3II II W .11
	_        _       a. Vs —a.a;
	0      0       1     —2—3
	I                                 II W 3II II W .11 7

Этот случай описывает волны, распространяющиеся перпендикулярно диэлектрическому слою.

Для того, чтобы записать систему уравнений Максвелла в пространственно-частотном представлении, необходимо найти матричные элементы оператора Н в пространственно-частотном представлении.

Матричные элементы оператора Н имеют вид:

H_a"^¹ =    Pm (©. ,©2 ) FFmK т \f У (12)

а , а 2 s              rm      1 2                     a j a 2 a j a 2 □

m

где P_m ⁿ - матрица, обратная к матрице парных скалярных произведений базисных векторов (10),

G © 1 ©2 ₌ a^ 2

^a 1 ^a 2

> ©1 © 2 ^a 1 ^a 2

A © 1 © 2

^a 1 ^a 2

= s (©1 — a1, ©2 — a 2) Q —

—6(©1 — a1, ©2 — a2)

> © 1 © 2 ^a 1 ^a 2

— 1 0

= —6 (“| — a1, ©2 — a2) Q —

—s(©1 — a1, ©2 —a 2)

Q =

— 1 0

s ( © 1 , © ₂ ) - преобразование Фурье от распределения диэлектрической проницаемости.

Система уравнений Максвелла в пространственно-частотном представлении имеет вид системы интегро-дифференциальных уравнений

i d f

k d x 3

+» +»

= SJ J H уm ( x 3 ) f ^a 1 ^a 2 m ( x 3 ) d a 1 d a 2 m —»—»

Для многих задач вместо базиса, состоящего из волн различной поляризации, распространяющихся в различных направлениях, удобно использовать следующий базис

где || W i |I, i = 1,2,3,4 - нормировочные коэффициенты, обеспечивающие нормировку введенного базиса.

2. Решение эталонной задачи

Предварительно рассмотрим задачу дифракции света на эталонном ДОЭ. Модельный ДОЭ должен сочетать в себе функции расщепителя пучка (дифракционной решетки) и при этом обладать фокусирующими свойствами. Такая модель позволяет охватить достаточно широкий класс существующих ДОЭ.

Для модельного расчета можно выбрать ДОЭ, расположенный перпендикулярно оси x ₃ в области 0 <  x ₃ <  D (рис. 1).

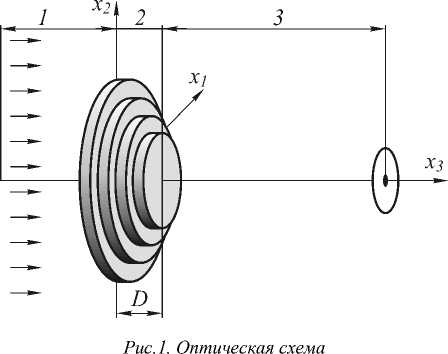
Диэлектрическая проницаемость в области эталонного ДОЭ имеет вид

^s ( x 1 , x 2 ) = Z g n exp ( ^ik ng ( x 1 , ^x 2 ) ) ,              (19)

n где x = (x1, x2) - декартовые координаты в плоскости оптического элемента, D – толщина диэлектрического слоя, n - целое число, x0 - точка на оптическом элементе в окрестности которой ищется поле. Функция g (x1, x2) имеет смысл функции эйконала для геометрооптического фокусатора [16-18].

Пусть функция g ( x 1 , x ₂ ) является квадратичной формой

g ( x 1 , x 2 ) = g ( x 0 ) + ( ^V g ( x 0 )( x - x 0 ) ) +

¹ M +—( x

- x o ) T ^M ( x o )( x - x o ) ,

D mm 2 ( © 1 , © 2 ) =

ik

•

ik

•

а матрица M имеет вид:

M =

a

c

c b

Для того чтобы решить задачу необходимо найти решение внутри ДОЭ (внутри диэлектрического слоя) и в свободном пространстве, удовлетворяющее условию непрерывности на границах раздела ДОЭ и окружающей среды.

2.1. Решение в диэлектрическом слое

Для получения решения внутри диэлектрического слоя в окрестности точки x ₀ = ( ( x 0 ) ₁, ( x 0 ) ₂ ) введем новые координаты у = ( y 1 , у ₂ ) :

x₁ - ( x 0 ) ₁      cos ( 9 ) - sin ( 9 ) Г у₁

^Х 2 ^- ( x 0 ) ₂ J L sin ( ⁹ )    cos ( ⁹ ) JL У 2

В этих координатах функция g ( x₁, x ₂ ) имеет вид:

g ( У 1 , У 2 ) = g ⁰ ( ^0, ° ) ⁺ Y T ( ^у ) ⁺ 2 ( ^у ) T M 1 ( y ) >    ⁽²²⁾

где матрица M ₁ имеет диагональный вид:

M 1 = Z^TMZ =

P i

в

cos ( 9 ) - sin ( 9 ) sin ( 9 ) cos ( 9 )

Угол 9 выбирается таким образом, чтобы матрица M 1 = Z^TMZ была диагональной.

Запишем Фурье-образ диэлектрической проницаемости

^£ ( © 1 , © 2 ) = Е g m ^ex P ( ikmg ( ^0,0 ) ) ^х m                                    (24)

^{х D}mm ( © 1 ^- m Y 1 , © 2 ^- m Y 2 ) ,

^{£ - 1} ( © 1 , © 2 ) = E g m ¹ exp ( ikmg ( ^0,0 ) ) ^X m                                  (25)

^{X D}mm ( © 1 - m Y 1 , © 2 - m Y 2 ) ,

Y ₁ и y ₂ связаны с производными функции g ( x ₁, x ₂ ) в исходной системе координат следующим образом

5 g ( x p ^x 2 ) d x ₁

d g ( ^x 1 , x 2 ) d x ₂

cos ( 9 ) - sin ( 9 ) y ₁ sin ( 9 ) cos ( 9 ) y ₂

• exp

г г

- ik

2 п т Д   2 п m₂ в ₂

( © 1 ) ² , ( © 2 ) 2 2 m^ 2 m ₂ P ₂

.

Связь поля в координатном и пространственно-частотном представлении имеет вид, аналогичный (8):

I W ( У1, У2 )) = да да

= EJJ f ^W ( x 3 )| F_w)

(28a)

s -да -да x exp (ik (a1 y1 +a2 у 2)) d a1 d a2.

Найдем матричные элементы оператора Гамильтона-Максвелла в пространственно-частотном представлении (13). Оператор Гамильтона-Максвелла для распределения диэлектрической проницаемости (24)-(25) имеет вид (12), где

^G ©© = E ^Gn ₁ ⁽ © 1 , © 2 , ^a 1 , ^a 2 ^)X

n ₁

^X D-v, ( © 1 - n 1 Y 1 ^-a 1 , © 2

n 1 Y 2

a 2 ) ,

G n ( © 1 , © 2 , a 1 , a 2 ) =

⁰              A n ⁽ © 1 , © 2 , ^a 1 , ^a 2 )

_ ^В„_ ( © 1 , © 2 , ^a 1 , ^a 2 )              ⁰

.

где

A n-, ( © 1 , © 2 , ^a 1 , ^a 2 ) = g -' exP ( ^ik n 1 g ⁰ ( ^0,0 ) ) ^X

X

-I

-

■ ^a 2    ^a 1

■ ^a 2    ^a 1 _

⁵ П 1

-

1 0 ’

-® n ₁ ⁽© 1 ’© 2 , ^a 1 , ^a 2 )      ⁵ n ₁

^- g ^exP ( ^ikn1 g ( ⁰ , ⁰ ) )

-

.

-

-

- ©2

-

Двумерные матрицы, входящие в (13), представляются в виде:

^a 1 ^a 2

= Е Лч (©1, ©2, a1, a2 )X n1

^X D n 1 n 1 ( © 1 - n 1 Y 1 ^-a 1 , © 2

n 1 Y 2 ^-a 2 ) ,

B©a© =E Bn1 (©1, ©2, a1, a2 )X n1

^X D nn ( © 1 - ⁿ 1 Y 1 ^-a 1 , © 2 ^{- n} 1 Y 2 ^-a 2 ) .

Запишем матричные элементы оператора Гамильтона-Максвелла в пространственно-частотном базисе (18)

H2n^n =yM©1©2n|G 0) a a       \x a1a2 s      / i \               -1 V 1, 2, 1, 2 / a1a2 s / n1                                             (34)

^X D n 1 n 1 ( © 1 ^{- n} 1 Y 1 ^{- a} 1 , © 2 ^{- n} 1 Y 2 ^{- a} 2 ) .

Решение системы уравнений Максвелла в пространственно-частотном представлении запишем в виде:

v ^a 1 ^a 2 l ( x₃ ) =

= £ v ^{s , s 2} l ( x 3 ) D i s 2 ( a , ^- s ₁ Y ₁ -y a ₂ ^- s 2 y 2 -^ 2 ) , ⁽³⁵⁾ s ₁ s ₂

§ , , c ₂ - произвольные постоянные, описывающие наклон падающей волны по отношению к локальной решетке.

Подставляем выражения в исходную систему интегро-дифференциальных уравнений Максвелла в пространственно-частотном представлении (17), получаем систему дифференциальных уравнений i _dvm m2l (x3)

7 E---л----Dmm (to - m,Yi - k m,m2      Оx3         1 2

-^L ^to 2 ^- m 2 ^Y 2 -7 ) =

+w +^

=ш / 'V ' ^( to , , ® 2 , a , , a 2 )| V^ q ) X (36) s , ^s 2 ⁿ 1 ^q -ю-то

Xvs,s2q (X3)Dss2 (a, -s,y, -^,a2 -s2Y2 -§2)x xDnn (to, -n,y, -a,,to2 -n,y2 -a2)da,da2.

Вычислим интеграл в правой части (36) методом стационарной фазы [10-12].

Получим:

i к ^

m ₁ m ₂

d v ^{m , m 2 1} ( x ₃ )

----------- X dx3

^X D m , m ₂ ( to - m Yl -У to - m 2 Y 2 - § 2 ) =

= Уy(vtoto2l\G„ (to,,to2,as,asllv, , V nV , , 2, , , 2/| a,s a 2 q/ s s2n q xvss2q (x3)x D         (to, - (n, + s,)y, -

3           s , + n , s 2 + n 2        , i i i

-7 , ^to 2 ^{- ( n} , + s 2^{) y} 2 -7 ) ,

где стационарные точки a. = § toV-SJi., n, + s, a2 = c2 +

( to 2 2 ) ^s 2 n , + s ₂

Введем новые обозначения для индексов суммирования в правой части (37)

m , = n , + s , ,     m ₂ = n , + s ₂.

Тогда в этой новой индексации i      dvm,m21 (x3)

— 7 ----—- X кchc m m2

^X D m , m ₂ ( to - m Y1 -^ , , ^to 2 - m 2 Y 2 "^ 2 ) =

= EEV'to"‘llG-. (to,to2.a:.«'2)|V.,.„)x(38)

^{m m} 2 ^{n q}

X v m , - n , m 2 - n , ^q ( x 3 ) x

XDm,m2 (to - m, Y1 -^, , to2 - m2 Y2 -^2 ) , и стационарные точки s        (to,-M( m, - n, )

^al 4i ⁺                         ,

m s         (to2 -^2 )( m 2 - n, )

a 2 = c2 +  -------—--------.

m ₂

Основной вклад в результат вносит функция

D m , m 2 ( to ^- m , Y , -^ , , ^to 2 ^- m 2 Y 2 - § 2 )

в окрестности точек to, = m, Y,+§,, to2 = m 2 y2 +§2.

Заменим в выражении для стационарных точек to , , to ₂ этими значениями.

Далее будем использовать стационарные точки as =§, +Y, (m, - n,), a2 = §2 + Y2 (m2 - n,).

Эта замена при малых длинах волн не влияет на точность вычисления интеграла методом стационарной фазы.

Уравнение (38) является функциональным уравнением, так как в него входит зависимость от to , , to ₂.

Перейдем от дифференциально-функционального уравнения к системе обыкновенных дифференциальных уравнений. Для этого выберем систему линейно-независимых функций K_mn ( to , , to ₂ ) .

Умножим (38) на каждую из базисных функций и в результате получим систему обыкновенных дифференциальных уравнений для коэффициен- mml тов v ^{m 1 m 2} .

Бивекторное поле внутри диэлектрического слоя имеет вид:

I W 2^aa ( x 3 )) = v ^a,a2 - ( x 3 )| V ^2,) +

+ v ^{a , a} 2 ² ( x 3 )| V_a^ +

+ v ^aia 2 3 ( x 3 )| V _{aia 2}3) +

+ v ^aia 2 4 ( x 3 )| '

где v ^a,“² ‘ ( x ₃ ) описывается выражением (35).

• 2.2.    Распространение в свободном пространстве

В пространстве с постоянной диэлектрической проницаемостью в плоскости x ₃ = 0 решение системы уравнений Максвелла в пространственно-частотном F -представлении запишем в виде:

/ ; ^2 l ( x 3 ) =

= E f i^{s , s 2} l ( 0 ) D s „2 ( a , - s , Y , -                       (40)

s ₁ s ₂

-§,, a2 - s2y2 -§2) exp (±ika3x3), a3

= ^! - a , - a 2

Знак «+» берется для 1 = 1,2; знак «-» берется, если 1 = 3,4.

Введем следующие обозначения:

• •    область 1 - область, в которой распространяется падающая и отраженная волны (обозначим I -падающая волна, соответствующая ТМ-поляри-зации, и R – падающая волна, соответствующая ТЕ-поляризации);

• •    f wi = i «№ h — коэффициент, описывающий па-

• дающую волну, соответствующую ТМ-поляри-зации. Соответствующий набор коэффициентов

f « 1 s 2¹ = I s s 2 e .

• •    f «ч^² = i «м e — коэффициент, описывающий падающую волну, соответствующую ТЕ-поляри-зации. Соответствующий набор коэффициентов f_i s i s 2 2 = I ^s 1 s 2 h ;

• •    f «m3 = r ^; x ^; 2 h — коэффициент, описывающий отраженную волну, соответствующую ТМ-поляри-зации. Соответствующий набор коэффициентов f₁ s^1S 2 ³ = R ^{1 2} e ;

• •    f «aR = r ^;; 2 e — коэффициент, описывающий от-

• раженную волну, соответствующую ТЕ-поляри-зации. Соответствующий набор коэффициентов f sis24 = Rss2h;

• •    область 2 - область, содержащая диэлектрический слой с плоскими границами;

• •    область 3 - область, в которой распространяется прошедшая волна;

• •    f “А2 1 = т »»2 e — коэффициент, описывающий прошедшую волну, соответствующую ТМ-поляриза-ции. Соответствующий набор коэффициентов f ' s 2 ¹ = J⁵ !s 2 e ;

• •    f 3 ^2 2 = y 3 ^;; - e — коэффициент, описывающий прошедшую волну, соответствующую ТЕ-поляризации. Соответствующий набор коэффициентов f ' s 2 ² = J s 1 s 2 h

Бивекторное поле в первой области имеет вид:

| W ( % 3 )} = I ^{a 1 a} 2 h ( % 3 )| F ^) +

+ 1 e ( % 3 )| F <,<-) +

+ R -*¹ " ² h ( % 3 )| F ^) +

+ R e ( % 3 )| F ^}.

Бивекторное поле в третьей области имеет вид:

I W     ( % 3 )} = T ^a1a 2 h ( % 3 )| F „ 1 „ 2 1) +

+ T e ( % 3 )| F ^}.

Используя (40) и введенные выше обозначения для коэффициентов, получаем выражение для поля в пространственно-частотном представлении.

• 2.3.    Сшивка решений

В предыдущих пунктах были записаны решения системы уравнений Максвелла в пространственночастотном представлении в области диэлектрического слоя и в области свободного пространства в виде линейной комбинации с неизвестными коэффициентами. В настоящем пункте рассмотрим решение задачи дифракции плоской волны на диэлектрическом слое с диэлектрической проницаемостью s , представленной в форме (19).

Условие сшивки на первой границе – равенство бивекторных полей на границе раздела

W " ¹ " ² ( 0 ) = W 2 « •" ( 0 ) .                               (43)

Условие сшивки на второй границе - аналогично (43):

W _! ^; - “ 2 ( D ) = W3^a^ ( D ) ,                        (44)

где D – толщина диэлектрического слоя.

Эти условия служат для определения коэффициентов T “ 1“² e , T “ 1 “ 2 h , R “ 1 “ 2 e , R “^ h . Таким образом, сшивка приводит к системе линейных алгебраических уравнений.

• 3.    Коротковолновые асимптотики

  • 3.1.    Поле внутри слоя модуляции ДОЭ

Рассмотрим теперь случай, когда длина волны освещающего пучка стремится к нулю (коротковолновая асимптотика). В этом случае

Dm-,m 2 ( ^ 1 , ® 2 ) = § ( Ю 1 , Ю 2 ) .                          ⁽⁴⁵⁾

Используя линейную независимость 5 -функций, получаем следующую систему линейных дифференциальных уравнений:

£ dvm1 m 21 (% 3) = k    d% 3

= z V ■"'■■ ’ | ^ ;. (» 0 » 0 , «г , «?)| V ., - . ?.) -          ( ⁴ 6)

ⁿ 1 ^q

■ vm1-n1m2-n1q (%3), где as' =^i +Y1 (m1 - n1), a2 = ^2 +Y2 (m2 - n1), to° = mY +§1, ro° = mгy2 +^2.

Запишем систему уравнений только для под- множества индексов m1 = m2.

£ dvmm11 (% 3) = k    d%3

= Z V^v ’■’■ ' I G .J» ; » ; , « st , « 2 t )| V;., ,, ,) ■          (47)

ⁿ 1 ^q

■ vm1-nm1-n1q (%3 ), где

a?' = ^, +Yi (mi - n), a2 = ^ + Y2 (m 1 — n),ю0 = m 1Y1 + £p to2 = miY2 + ^-

Далее введем новые индексы суммирования

P i = ^m 1 - n i :

i Svm11 (x3) = k dx3                                           (48)

= ZV*°1 \ Gm1-p Ж,af,«2)| Vs^q) • vPq(X3), p1 q где as' =^1+Y1 P1, a2' = ^2 + Y2P1, Ю0 = m1Y1 +^1, Ю0 = mW2 +^2-

Обозначим

Y ₁ = Y cos ф , Y ₂ = Y sin ф -

Легко показать, что справедливы тождества

^ + y cos ф p ₁    cos 9 - sin 9   ^ + y p ₁

c ₂ + y sin ф p ₁     [ sin 9    cos 9_| c ₂

cos 9 sin 9 ^ + y cos ф m₁ ^ + y cos ф m₁ - sin 9 cos 9 q ₂ + Y sin ф p ₁ ^ ₂ + y sin ф p ₁

-^ ₂ -у sin ф p ₁ ^ +y cos ф p ₁ cos 9 - sin 9

-^ ₂ - y sin ф p ₁ q ₂ +y cos ф p ₁ sin 9 cos 9

^ 1 +y m

-

^ 1 ⁺ Y P 1

-

Ч2 1 1 ⁺ Y P 1 .-1 2   1 1 +Y P 1

Структура оператора Гамильтона-Максвелла такова, что отличны от нуля только следующие восемь матричных элементов

H P 1 ¹ - = ^{V 61 62} | ^ m 1 - p 1 ⁽(0 1 , (0 2 , Ct. 1 , St 2 )| ^V a ₁ ,j ₂-^ >

H m¹* V ^{6 162} p m 1 - P 1 ^(to 1 , •”2 , ^a 1 ,•^ 2 )| ^V a ₁ a , 4) ’ H m- = ( ^{V 6 1 6 2} p m 1 - P 1 (C O 1 , •”2 , с⁵ 1 , с⁵ 2 )| V a ₁,2₂3^ , H^ = ^y ^{to to 2}| A_mi - P 1 ( ^to 1 , ^to 2 , ^a 1 , ^a 2 )| V a 1 a 24^ ,    (52)

H m;? = V ^{6 1 6 2} 3| B_mi- P 1 ( ^to 1 , ^to 2 , ^a 1 , ^a 2 )| V a 1 a 2 1) , ^Н а2 = V ^{6 1 6 2} B B - _ P 1 (to 1 , to 2 , a, 1 , a 2)| V a ₁₍ . 2 2) , ^H^ = ( ^{V 6 1 6 2} 4| ^Bm 1 - P 1 ( ^to 1 , ^to 2 , ^a 1 , ^a 2 )| ^V da 2 1) , H Pm ¹^ = y_V ^{toto 4}| B m - ^ 1 , ₆ 2 , ^a 1 , ^a 2 )| V a 1 ₆ 2 2) .

В последних выражениях использовались ненулевые компоненты соответствующих четырехмерных векторов.

Система распадается на две системы уравнений:

i dvm11 (x3) = k   dx 3                                          (53)

Z Z ну (x3 ) = ZZ АУ (x3).

P 1 q = 3,4                          P 1 q = 3,4

Используя эти тождества, можно доказать соот- ношение l=1, 2, toPtoP              /,^0 ,^0     ?' s.St

V ^V     |^G m - p ₁ ^(to 1 , ^to 2 , ^a 1 , ^a 2

Vst st a as q

1₁, ю ₂, a ₁, a ₂

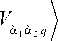
i dvml (x3) = k   dx 3

= ZZ H my^1q ( x 3 ) = ZZ B mql v "⁴ ( x 3 ) , P 1 q = ^1,2                           P 1 q = ^1,2

^a 1 =^ 1 +Y 1 P 1 , ^a 2 =^ 2 , to 1 = m ^ +1 1 , (0 2 =1 2 -

Следует отметить, что матричные элементы в правой части (49) соответствуют задаче конической дифракции [19] на одномерной периодической решетке.

Для дальнейшего анализа запишем уравнение в виде:

m1l iv = H^ (x-)■                     (50)

k dXo l=3, 4.

Полученные системы можно свести к системам уравнений второго порядка. При этом вдвое сокращается размерность системы уравнений:

J_ d2vm11 (x3 ) k2 d(x3)2

= M^m‘vn ( x 3 ) ,

vs11 (x3 ) = Z Emn (a + mn exp (ik^mnx3 ) + mn где

H m^l = p ₁ q

ю ₁ ■ ю ₂, a ₁, a ₂

(5 )

+ a - mn exp ( ^{- ik} Ц mn ( ^x 3 ^- D ) ) ) ,

Z MnlEPn =^2P„EPqn, nl ml                ml pq ns z z ^ Pq ns , P q=3,4

l =1, 2,

d ² v m^{1 1} ( X 3 ) k^{2 д} ( x з ) ²

= On ( X 3 ) ,

v s ¹ l ( x 3 ) = E P^ ( a ⁺ "’ exp ( ik Ц mn x 3 ) ⁺ mn

+ a - ^mn exp ( - ik ц mn ( x 3 - D ) ) ) ,

EMsqPpl = U2 Psq pl mn    цmn mn , pl

Nm = v^ у Bm Apq ns                   pq ns , p q=1,2

l =3, 4,

D - толщина диэлектрического слоя.

В случае, когда плоская волна падает перпендикулярно к плоскости дифракционного оптического элемента, или радиально-симметричная волна падает на радиально-симметричный оптический элемент, имеем частный случай | , = 0. В этом случае уравнения для коэффициентов, описывающих распространение поля внутри слоя, имеют вид:

R ^a 1 ^a 2 e ( x ₃ ) =

= ERse5(at - sY1 -^1, a 2 - sy2 -^2 )x s1

x exp ( - ik a ₃ x ₃

R " h ( x 3 ) =

= ERs5 («1 - sY1 - ^, «2 - sY2 - ^2 ) x s1

x exp ( - ik a ₃ x ₃ ) .

Для прошедшего поля

Ta1«2e (x3 ) = ETse5(«1 -s1Y1 - s1

• -^ ₁₅ a ₂ - s 1 Y ₂ -^ ₂ ) exp ( ik a ₃ ( x ₃ - D ) ) ,

Ta1a2h (x3) = ETsh5(a1 -s1Y1 - s1

• -^ ₁₅ a ₂ - s 1 Y ₂ -^ ₂ ) exp ( ik a ₃ ( x ₃ - D ) ) .

3.3. Условия сшивки полей

),

i д v m¹¹ ( X 3 )

к    д x ₃

= a ; ; 1 v p¹³ ( x 3 ) ,

i д vm12 (xj       , s к    дZ 3 = Am4vp14 (x3),                     (58)

Условие непрерывности электрического и магнитного полей приводит к формулам для расчета локальных коэффициентов отражения и пропускания:

v s^1k ( 0 ) = Ph ( 0 ) ( Г ^a 1 ^a 2 ^k|| F a 1 a ₂1) +

i д vm13 (xj       3 X к Л     = Ami3 vp11 (x3),                       (59)

+ Is^E ( 0 ) V ^a 1 ^a 2 ^k||F a 1 a 22) +

+ R s ¹ h ( 0 )( Г ^{a 1 a} 2 ^k\\ F^ +

+ R s ¹ e ( 0 ) ( Г ^k||F a 1 a ₂4) ,

i д v m ^{1 4} ( x 3 ) к    д z

= A m4 v p¹² ( x 3 ) .

v s^k ( D ) = T ¹ ( D ) V ^aa2 ^k|| F aa ₂1) +

+ T s ^{1 k} ( D ) V

a] a₂ k

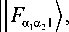
При стремлении длины волны освещающего пучка к нулю выражение для поля внутри слоя имеет вид:

v “'“ 2 l ( x ₃ ) =

= E ^vs ¹ l ( ^x 3 ) 3 ( a ^- s 1 Y 1 -^ , ° 2 ^- s ^2 Л ) .

s ₁

где a, = s ₁ y + § ₁, a 2 = s ! Y + ^ 2 -

Нетрудно показать, что преобразование поворота не изменяет скалярное произведение a1a2 k

II f \ = V a1a 2 k\U \ a1a2 s /     \                a 1OL2 s / где a 1 = s1Y + ^1, a2 = sfy + ^2-

Следует отметить, что полученная система линейных уравнений совпадает с системой уравнений для определения коэффициентов дифракционной решетки в случае конической дифракции [2, 19].

3.4. Поле на выходе оптического элемента в случае ^ ₂ = 0

В случае, когда плоская волна падает перпендикулярно к плоскости дифракционного оптического элемента, или радиально-симметричная волна падает на радиально-симметричный оптический элемент, имеем частный случай j|₂ = 0. Учитывая формулы (28a), поле на выходе ДОЭ в пространственном представлении в переменных y ₁, y ₂ имеет вид:

W =

= ( f f r '"2 ' ( x )| F A + Г h ( x )| 1= ,)(x    (64)

111         \ 3 / aj 02 1 /             у 3 / ULj 02 2/1        x /

—x> —x> xexp( ik (a1 y1 + a2 y 2) x3) d a1 d a2, где F a2 m) — базисные вектора F-представления.

Коэффициенты T ^{s 1 e} , T ^{s 1 h} , входящие в выражения (62), для случая . 2 = 0 имеют вид:

Г ¹ e = а ( 0,0 ) T h ¹ ( 0,0 ) ; Г ¹ = b ( 0,0 ) T ¹ ( 0,0 ) .

Коэффициент а ( 0,0 ) описывает вклад падающей волны в случае, когда направление электрического поля совпадает с направлением штрихов локальной дифракционной решетки.

Коэффициент b ( 0,0 ) описывает вклад падающей волны в случае, когда направление магнитного поля совпадает с направлением штрихов локальной дифракционной решетки. T h ¹ ( 0,0 ) , Г ¹ ( 0,0 ) - коэффициенты дифракции в s ₁ порядке для случая, когда направление магнитного и электрического (соответственно) поля параллельно штрихам дифракционной решетки.

Вычисляем интеграл в выражении (64), получаем поле в пространственном представлении в переменных y ₁, y ₂

| W ( у )) = £ а ( ^0, О ) Г;( 0,0 )| F^^ „ 1 ₊ , ₂1 n ₁

x exp ( ikn g ( 0,0 ) ) exp ( ik Y у n 1 ) +

+Z b (0,0) Г (0.0)1 F+„„+U x n1

x exp ( ikn g ( 0,0 ) ) exp ( ik Y у n 1 ) .

Теперь необходимо перейти от координат y ₁, y ₂ к координатам x ₁, x ₂. Этот переход осуществляется с помощью преобразования вращения. Поле в точке x ₀

I W ( X 0 )) =

= 2 а ( ^0, 0 ) ^Th' ( ^0, 0 ) Zz| ^F .+„1„+_t,) x n ₁

x exp ( ikn g ( 0,0 ) ) +                             (66)

+ 2 b ( ⁰ , ⁰ ) ^T,' ( ⁰ , ⁰ ) ZZ|F .+,, , „+. ,,) x n ₁

x exp ( ikn 1 g ( 0,0 ) ) .

Матрица ZZ имеет вид

ZZ =

Z

Z

Напомним, что матрица Z имеет вид (23).

Для получения окончательного результата определим a и b , которые описывают падающую волну.

Бивектор электромагнитного поля падающей волны в плоскости x₃ = 0 в координатах ( у 1 , у ₂ ) , когда исходная электромагнитная волна падает перпендикулярно модулированной дифракционной решетке и вектор поляризации направлен вдоль оси x 2 , имеет вид:

W ( 0,0 ) = ( а ( X )| F ) + b ( Х 0 )| F 2 )) ,              (67)

где a3 cosф|I We||—1

| F\ = ^a3^sin ф| | We i Г¹

¹       - Sin фд/Ё|| W_e |I"’

_Ч cos ф-x/s 11 W e ll ¹ _?

sin ф(| | W_h || Vs)

। F^ = ^- cos ф (| W h U Vs ) Оз cos ф|| Wh||^-1

_ч Оз sin ф|| Wh||^-1

Y, ф = arctg—.

Y ₁

Базисные вектора выбраны таким образом, чтобы электрическое поле в первом базисном бивекторе и магнитное поле во втором базисном бивекторе были направлены вдоль штрихов локальной дифракционной решетки.

Поле (67) в координатах ( x ₁ , x ₂ ) описывается выражением

W ( X 0 ) = ZZ ( а ( X 0 )| Fh) + b ( X 0 )| F 2) ) ,            (69)

ZZ F 1

ZZ F 2

a ₃ cos to || W_e || ^{1 a} 3 ^{sin to}|| W e IГ' - sin toVs 11 We || * cos toVs| I W_e || ¹ ^

^{sin to} (| I W h ll Vs) - cos to ( I W h ll Vs ) a ₃cos to|| W_h || ¹

^ a ₃ sin to| I W_h||'

to = ф + 0 .

Бивектор, описывающий подающую волну в случае, когда она нормально падает на элемент, имеет вид:

W =

Vs

Для определения a и b необходимо решить систему линейных алгебраических уравнений

o "		- cos to		- sin to
1	= a	- sin to	+ b	cos to
vs		sin to Vs		- cos to Vs
o _		- cos toVs		- sin to Vs

В этом случае a = -V2sin(ф + 9), b = V2cos(ф + 9)

и окончательное выражение для электромагнитного поля на выходе модулированной дифракционной решетки имеет вид:

I W ( X o )) =

= 2 S ZZ ( - sin ( ф + 9 ) T n ( X o )| F . _hnv;h „ 1 ,1) +     (73)

n ₁

+ cos (ф + 9)Tn (xo )| FY1 „1Л2„1.2)) exp (i4 g (xo )) , где Ten1 = Ten1 (Xo) - Th' = T„ (Xo) - - коэффициенты дифракции на локальной решетке для Е- и Н-поля-ризации, соответственно. В случае, когда вектор поляризации направлен вдоль оси x1:

_ 1 " - cos to - sin to o - sin to cos to o = a sin to Vs +b - cos to Vs ,          (74) _Ve_ - cos toVs - sin to Vs a = -V2cos(ф + 9), b = -V2sin(ф + 9) -      (75)

и выражение для поля принимает вид:

I W ( X o )> =

= -V2 £ ZZ ( cos ( ф + 9 ) T „ ( X o )| F^ „ 1 -1) +    (76)

n ₁

+ sin ( ф + ⁹ ) T n ¹ ( ^X o ) | F Y 1 „ 1 , _{Y 2} „ 1 ,2 )) exp ( ^ik „_x g ( ^X o ) ) .

• 4.    Асимптотики

• 5.    Расчет поля фокусатора в кольцо

для псевдопериодических структур в рамках электромагнитной теории

В данном пункте рассмотрим применение вышеизложенных методов для расчета поля в случае дифракции волны на ДОЭ, которые обладают зонной структурой. В предыдущем разделе мы рассматривали дифракцию на модельном ДОЭ. Рас- смотрим теперь диэлектрический слой с диэлектрической проницаемостью, которая описывается выражением (19). Случай, когда функция g (x1, x2) является линейной, будет соответствовать чисто периодической структуре (дифракционной решетке). В случае, когда функция g (x,, x2) не является линейной, получаем дифракционную структуру с изменяющимся периодом.

Для того чтобы воспользоваться результатами предыдущего раздела, сделаем предположение о том, что поле в данной точке зависит от распределения диэлектрической проницаемости только в окрестности данной точки. Это предположение основано на принципе локализации, который рассмотрен выше. Далее разложим функцию g ( x , , x ₂ ) в окрестности точки X _o в ряд Тейлора с точностью до членов второго порядка.

Полученное выражение по форме совпадает с выражением для поля на выходе дифракционного оптического элемента, полученного в рамках метода нелинейного предыскажения фазы, рассмотренного в работах [16, 17]. Оно также объясняет возможность использования приближения тонкого оптического элемента. Отличие состоит в том, что коэффициенты T „ = T „ ( X _o ) и T „ = T „ ( X _o ) имеют другой физический смысл. Напомним, что в методе предыскажения коэффициент T_e „ ' = T_e „ ' ( X _o ) = T „ = T „ ( X _o ) совпадал с коэффициентом разложения в ряд Фурье функции предыскажения. В нашем случае он определяется согласно методу, изложенному в предыдущем разделе настоящей работы.

Рассмотрим поле от фокусатора в кольцо. В этом случае функция g ( r ) имеет вид:

g ( r ) =V ( ^{r - r}o ) ^{2 +} f ^{2, r} = V x ^{2 + x 2 ,          (77)}

r _o - радиус кольца фокусировки.

По аналогии с (76) следует, что электромагнитное поле на выходе дифракционного оптического элемента, фокусирующего в кольцо, имеет вид:

| W ( ^X 1^{- x} 2 )) =

Г r²

= V2exp l-| S ZZ ( T h„ F-„ o' +            (78)

X ) „

^{+ T}e„|^F Y „ o2) ) exP ( ^ik „g ( r ) ) ^,

dg (r)

Y =         "

d r

Были проведены расчеты распределения интенсивности электромагнитного излучения в фокальной плоскости фокусатора в кольцо для различных сочетаний параметров системы.

Вычисление поля проводилось на основе распределения поля на выходе ДОЭ (78) с помощью пропагатора, описанного в работе [13].

На рис. 2 приведены примеры расчета полей от фокусатора в кольцо для значений, указанных в табл. 1 (все размеры в мкм). При малых отношениях σ / f , где σ – параметр освещающего гауссова пучка, распределение интенсивности в фокальной плоскости фокусатора в кольцо близко к распределениям интенсивности, полученным в работах [18,20,21] в рамках скалярного приближения. В этом случае распределение энергии практически радиальносимметрично. При увеличении фокусного расстояния степень симметричности увеличивается. При увеличении отношения σ / f в распределении энергии вдоль кольца появляется асимметричность. Наличие асимметричности связано со следующими факторами:

• •    наличие линейной поляризации у падающей волны нарушает радиальную симметрию задачи, так как в разных точках фокальной плоскости электрические поля от различных точек на фоку-саторе приходят под разными углами;

• •    при увеличении отношения σ/ f появляется зависимость коэффициентов дифракции от направления локальной дифракционной решетки в случае линейной поляризации падающей волны.

Неравномерность интенсивности излучения в плоскости наблюдения на выходе из фокусатора в кольцо обусловлена неравномерностью значений коэффициентов пропускания (отражения) Е - и Н -поля-ризации в зависимости от текущего значения периода зонной структуры (дифракционной решетки).

Заключение

В данной статье представлен асимптотический метод решения задач дифракции на ДОЭ, который сочетает в себе решение задачи дифракции на периодической структуре с периодом сравнимым с длиной волны и геометрооптический подход. Решена задача дифракции на эталонной квазипериодиче-ской структуре, сочетающей в себе функции расщепителя пучка и дифракционной линзы. На основе решения эталонной задачи получено простое выражение для поля в плоскости, непосредственно прилегающей к ДОЭ. Полученное выражение позволяет оценить распределение поля на выходе ДОЭ, не прибегая к сложным вычислительным методам.

Работа выполнена при поддержке грантов РФФИ 07-07-97601, 07-07-96602, 08-07-99005, 07-07-91580-АСП, а также российско-американской программы «Фундаментальные исследования и высшее образование» (“BRHE”).

Таблица 1

Параметр	Значение (вариант 1), мкм	Значение (вариант 2), мкм
Длина волны λ	1	0,1
Параметр гауссова пучка σ	50	50
Расстояние от оптического элемента до плоскости наблюдения	1000	100
Фокусное расстояние	1000	100
Габаритные размеры оптического элемента	500×500	500×500

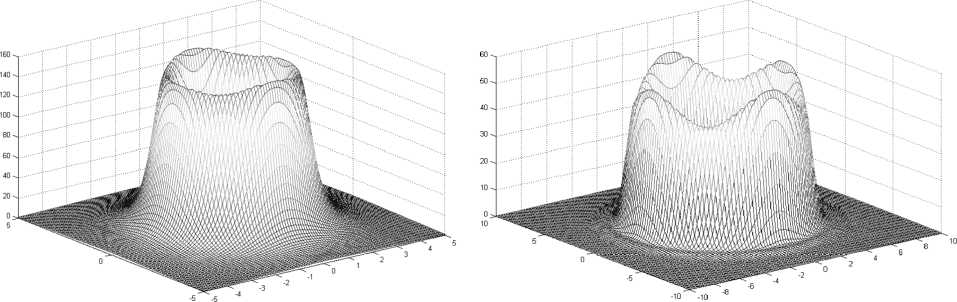
Рис. 2. Рассчитанные распределения интенсивности поля в фокальных плоскостях фокусаторов в кольцо с параметрами, приведенными в Табл. 1 (вариант 1 – слева; вариант 2 – справа).