Асимптотический метод решения контактных задач о действии полуполосового штампа на анизотропный композит

ВЕСТНИК ПНИПУ. МЕХАНИКА № 2, 2025PNRPU MECHANICS BULLETIN

Контактные и смешанные задачи о действии полупо-лосовых штампов на анизотропные композиты актуальны во многих областях. Это проблемы инженерной практики при конструировании сложного оборудования и узлов с контактами на основе конструкционных композитов [1–14], в строительстве – фундаментостроение, фрикционное взаимодействие, при конструировании ленточных фундаментов [15; 16], в электронике – в преобразователях на поверхностных акустических волнах и в полосковых линиях передач [17]. Эти проблемы возникли в науках о Земле, в сейсмологии, для исследования сейсмичности зон перехода горной гряды в равнину [18]. Разработан ряд аналитических и численных приближенных методов решения этой задачи, в основном базирующихся на решении задач для бесконечной полосы, с последующим делением носителя решения на две половины [19]. Для численного решения методом граничного элемента задача является сложной в связи с наличием на всей границе штампа концентрации контактных напряжений. Заметим, что в работах [20–26] применялись в основном численные методы для решения различных граничных задач для анизотропных композитов.

Особое место в контактных задачах с негладкой границей у штампов занимают угловые точки границы с повышенной концентрацией контактных напряжений, где только в последнее время достигнут значительный прогресс [27]. Аналитическое построение точного или высокоточного приближенного решения этой задачи сдерживалось в связи с отсутствием аналогов формул Сохоцкого – Племеля для функций нескольких комплексных переменных, что пока не удалось построить. Однако определенное продвижение в этих задачах наметилось в связи с разработкой метода блочного элемента, позволившего точно решать контактные задачи в четверти плоскости [28].

Именно построение решений этих контактных задач, как показано в настоящем исследовании, позволило построить асимптотическое решение контактной задачи для полуполосы, приближающееся к точному при увеличении ширины полосы.

Далее показано, насколько значительно отличие решения для полуполосы, получаемое простым делением носителя решения для полосы на две части, от асимптотически верного решения.

Постановка задачи

Интегральные уравнения о действии в статическом режиме полосового и полуполосового штампов на анизотропную среду (рис. 1) имеют соответственно вид [19, 29–31]:

∞ ^c 1

К q = j I k ( x -^ , y -n ) q ( ^ , П ) d ^ d П =

-∞ - c ₁

= f ( x , y ), -∞≤ x ≤∞ , - c ₁ ≤ y ≤ c ₁;

k ( x , y ) =

4 π ²

∞∞

J J K ( а , в ) e " ^{+e y}) d a d в ;

-∞ -∞

∞ c

К q = J J k ( x -^ , y -n ) q & П ) d ^ d n = f ( x • У )•

0 - c

0 ≤ x ≤∞ , - c ≤ y ≤ c ;

k ( x , y )

∞∞

= ¹          K ( α , β ) e ^{- i ( α x +β y )} d α d β .

4 π ²

-∞ -∞

Рис. 1 Полосовой штамп имеет протяженность до бесконечности в обе стороны

Fig. 1. The half-strip stamp has an infinite extension in both directions

c

- c

Рис. 2. Полуполосовой штамп имеет протяженность до бесконечности только справа

Fig. 2. The half-strip stamp has an infinite extension only on the right

В общем случае функция K (α, β) является комплекснозначной двух комплексных переменных, может иметь особенности в виде полюсов и точек ветвления, не лежащих на контурах интегрирования. Она порождается решением анизотропной граничной задачи в многослойной среде. Способ построения интегрального уравнения для многослойной изотропной и анизотропной сред детально описан в работах [19; 29–31]. Он сводится к построению функции Грина применением преобразования Фурье по горизонтальным координатам граничной задачи в слое с последующим решением одномерных задач, которые решаются рекуррентными формулами в случае постоянных физикомеханических параметров среды [30], либо решением одномерных обыкновенных дифференциальных уравнений с переменными коэффициентами в случаях переменных физико-механических параметров [31].

В контактных задачах для многослойной среды внешнее воздействие определяется путем решения соответствующего интегрального уравнения [19; 29–31]. Если отказываться от решения интегрального уравнения и принимать контактные напряжения исходя из «здравого смысла», то проблема решается, но как сильно она отличается от точного – неизвестно. Решения контактных задач характеризуются наличием особенностей по границам штампа, даже если они закруглены в угловых точках. Однако инженерная практика показала необходимость их учета [27; 31], так как не все технологически допустимо закруглять. Ряд примеров интегральных уравнений для анизотропных композитов приводится в работах [29; 30].

Функция K (α, β) является непрерывной, суммируемой на осях по обоим аргументам, с поведением на бесконечности вида

K ( α , β ) = O ( α ^{- 1} ), β = const;

K ( α , β ) = O ( β ^{- 1} ), α = const, α , β→∞ .

Контактная задача для полосового штампа

Решению задачи для уравнения (2) предшествует построение решения контактной задачи для полосового штампа, уравнение (1), которая была рассмотрена в [19].

Его асимптотическое решение для c ₁ >>  1 было построено путем суперпозиции решений трех интегральных уравнений, в которые вырождается исходное интегральное уравнение в предположении роста относительной ширины 2 c ₁ полосы. Эти уравнения получались путем попеременного устремления верхней и нижней границ полосы к бесконечности, а третьим оказалось уравнение свертки во всей плоскости. Построенные интегральные уравнения, допускающие обращение, позволили сконструировать асимптотическое решение. Оно оказалось эффективным, поскольку с высокой точностью привело к сопряжению со встречным асимптотическим решением, полученным другим методом для c ₁ <<  1 [19].

В связи с важностью этого подхода для решения интегрального уравнения (2) ниже дается более детальное рассмотрение способа асимптотического решения уравнения (1) для c ₁ >>  1 . Описанный выше подход привел к решению двух интегральных уравнений Винера – Хопфа и уравнения свертки, имеющих вид

∞∞

К 9 11 = J J k ( x -^ , У -n ) M^n ) d ^ d n = f ( x • У )•

-∞ - c ₁

f ^{1 (} x • ^y ) = { 0

∞ ^c 1

^К q 21 = J J

-∞ -∞

^f ■ x • ^y) =^{ 0

f ( x , y ),   -∞ ≤ x ≤ ∞ ,   - c ₁ ≤ y ≤ ∞

-∞≤ x ≤∞ , -∞≤ y ≤- c ₁, c ₁ ≤ y ≤∞ ,

k ( x -ξ , y -η ) q ₂₁( ξ , η ) d ξ d η= f ₂( x , y ),

f ( x , y ), -∞ ≤ x ≤ ∞ , -∞ ≤ y ≤ c ₁

-∞≤ x ≤∞ , -∞≤ y ≤- c ₁, c ₁ ≤ y ≤∞ ,

∞∞

К q 31 = J J k ( x -^ , У -n ) q 31& n ) d ^ d n = f , ( x• y )•

-∞ -∞ f3(x, y)

f ( x , y ),   -∞≤ x ≤∞ ,   y ≤ c ₁

0 -∞≤ x ≤∞ , y ≥ c ₁.

Руководствуясь требованием перехода асимптотического решения к вырожденной составляющей, при стремлении обеих границ полосы к бесконечности асимптотическое решение уравнения (1) на основании решений уравнений (4) приняло вид

q ⁽ x , y ) = q _n ⁽ x , y ) + q 21 ⁽ x , y ) - q 31 ⁽ x , y )■ (5)

Позже, когда методом блочного элемента была выведена точная система интегральных уравнений для полосы, эквивалентная уравнению (1) [19], ее первое приближение при решении для q >>  1 совпало с (5). Таким образом, установлено, что асимптотическое решение интегральных уравнений, получаемых расширением границ полосы, действительно приводит к построению асимптотического решения.

Решение интегральных уравнений (4) получается применением метода Винера - Хопфа, при этом используются следующие операторы преобразования, что детально описано в [29; 31]. Они применимы для анизотропных композитов и имеют вид

{ G ( а , в )}_+а = -17 J G^ d S , аеп ; , 2 п i г ;-а

{ G ( а , Р )Ц =- -1т J G^ d ^ , ае П ; , ^а 2 п i Г 1 s — а

{ G < “ - в ) } +_е = i f G ot d 'Реп; , ^{2 П} i Г 2 П^_в

^{{ G (} ° ,^р» -р =- i^ d n, ^веП ',

1 fln K (S Р)^      ТГ+

^K ;а ⁽«- ^{Р )} = exP^   /   ^{d S аеП}« ,

2 n i Г 1 S — а

K —а ( а , в ) = exp ^f - -Lpn K O d S1 , аеП ^- , 2 n i’ с-а

\                 1 1/

1 f^ln K (а, n) , д _n+

K+p(а,Р) = exP— -----— dП- 3е ПР, в             2п irJ   n-Р г t                 1 !1пК (а, П) ,

K-р(а,Р) = exP - — I

3              2п t>   n-Р , ве Пр.

Здесь п ; , П _а - комплексные области выше, плюс, и ниже, минус, вещественной оси o а , комплексной плоскости а , а П ; , П - - области верхняя, плюс, и нижняя, минус, вещественной оси о Р комплексной плоскости Р ■

При помощи этих операторов удается компактно записать решения уравнений (3) с учетом геометрического расположения вспомогательных уравнений (4) в координатной системе на плоскости. Чтобы записать решения интегральных уравнений (4) в исходной системе координат xoy , надо воспользоваться решением q_n ( x , y ) эталонного уравнения Винера - Хопфа, имеющего вид

∞∞

^К q n = j j ^{k (} x "  ^S "  ’ У " ^- П n ) q n ^{( C} n , П n ) ^{d с} _n ^d П n =

-w 0

= fn ⁽ x n , У п ), ^-j < x n ⁰ <  У п

∞∞ qn (xn , Уп ) = .J I" Qn («- P)e~i(ax■ +Py" ’dаdP,     (7)

4 n

-∞-∞

∞∞

k ( X " , У " ) = —И J K " ( а , P ) e -^{i( a x} " ^{;P y} " ) d a d p ,

4n J J

-∞-∞

∞∞

F n ( a , p ) = f f f " ( S " , n n ) e ^{i ( a x} " ^{+p y} " ) d S " d n n , "  = 1,2.

0 0

Его решение в преобразованиях Фурье, строящееся традиционным методом Винера - Хопфа, представимо в форме

Q n ( a , Р ) = K " +p ( а , Р ) { K ; -p ( а , Р ) F " ( а , Р ) } +_р =

= K " ( а , Р ) F " ( а , Р ) -                  (8)

- К^ ( а , Р ) { K " --p ( а , Р ) F " ( а , Р ) } -_Р , п = 1,2.

Чтобы воспользоваться этим решением для обращения интегральных уравнений (4), достаточно выполнить некоторые преобразования координат. Так, для получения решения qN(x, y) первого уравнения в (4) необходимо воспользоваться формулами (7), (8), внеся следующие замены f (a,Ух) ^ Л(а,-С1 + УЛ             (9)

K 1 ( а , Р ) ^ K ( а , Р ), q _n( x , y ) ^ q i ( x , y + C i ).

Чтобы получить решение q21(x, y) второго уравнения, необходимо в формулах (7), (8) принять f г(а, У2) ^ f Л0, Ci - У2), K2(a,Р) ^ K(a,-Р), (10) q 2i( x, y) ^ q 2(x, ci - У )).

Третье уравнение свертки решается применением преобразования Фурье по обеим координатам, и решение имеет вид ∞∞ q31(x, y) =      f f k~'(a, Р)F3(a, Р)e "^+Рy)dadР.

4n2 J J

-∞-∞

В результате после сокращений асимптотическое решение для полосового штампа при c >>  1 можно выписать в следующем виде:

q ( x , y ) =       J j [ Q i ( a , Р ) e -i^{( a x +Р y} ) -

4 п J ^J

-∞-∞

- Q ₂( a , Р ) e "^ ^{+Р ( y ; 4))} -

- Q ₃ ( a , Р ) e ^{- i( a x +Р ( c - y} )) ] d a d Р + O ( c ^{- 1} ) Q i ( a , Р ) = K ^{- 1} ( a , Р ) F ( a , Р ), Q 2 ( 0 , Р ) =

= K ;Р ( а , Р ) { K - ^- Р ( а , Р ) F ( a , Р ) } _-р , Q 3 ( а , Р ) = K ;Р ( а , -Р ) { K - ^- Р ( а , -Р ) F 2 ( а , Р ) } _ _Р

Здесь первый справа член представляет вырожденную составляющую решения, соответствующую случаю, когда у полосы удалены обе границы. Второй и третий члены описывают поведение контактных напряжений при приближении к границам у = —c1 и y = c1 соответ ственно. Концентрации контактных напряжений в обла сти |у| < c1 описываются функциями (^у + c1 )   и

( ^c ₁ — у ) соответственно [19].

Контактная задача для полуполосового штампа

Используем описанный выше подход к построению асимптотического решения интегрального уравнения (3) для полуполосового штампа большой относительной ширины, c >>  1. Введем в рассмотрение следующие три интегральных уравнения Винера - Хопфа:

Q n ( a , в ) = K"F n — 2 [ K —« { K —a F n } —„ +

+ K n —в { K n —в F n } —₽ +

+ K n —L₽ { K n —U I K n —a F n L } —в +

+ K n — M K n —в—_а { K n —в ^F } +в L ] .

По аналогии с (9), (10) для случая полуполосы имеют место следующие соотношения для первого уравнения (12):

^f .^{( x} 1 , y j = ^{f ( x} 1 , ^{— c +} y 1 )> ^K 1^{( a} , ^{в )} = ^{K ( a} , ^{в )} , q 12^{( x} , у ) = q 1^{( x} , у ^{+ c} ).

Для второго уравнения (12)

f2( x 2, у 2) = f(x 2, c — у 2)  K 2(a, в) = K(a, —в), q 22(x, у) = q 2(x,c—у).

те те

K q 1 = J J k ( x — ^ у — n ) 9 1Й, n ) d ^ d n = ft ( x , У ), 0 — c

^f i ⁽ x , У ) =

^{f (} x , У ),  ⁰ <  x <^те,  | y | <  ^c

— те <  x <  0, — те <  у < — c , C <  у < те ,

те

K q ₂ = J

c

J k ( x — ^ , у — n ) q ₂( ^ , П ) d ^ d П = f > ( x , у ), 0 <  x < те ,

—те

Для третьего интегрального уравнения в (12) решение строится непосредственным обращением уравнения методом Винера - Хопфа и имеет в преобразованиях Фурье вид

^f 2 ⁽ x , у ) =

^{f (} x , у ),

0 <  x < те, | у | <  c

— те< у < — c , c < у <те ,

тете

K q 3 = J f k ( x — ^ , у — n ) q 3& n ) d ^ d П = f ₍( x , у ),

0 —те

^f з ⁽ x , у ) = •

^{f ( x} , у ).  ⁰ <  ^x <“ , | у | <  ^c

0, 0 <  x <те , | у | >  c

0, — те <  x <  0, — те <  у < те .

q 32 (x , у ) = 4 - 2 J J Q ( a , в ) e ^{+в y} ’ d a d в

Q ( a , в ) = K^ ( a , в ) { K — ^— a ( a , в ) F ( a , в ) } _+a -- K iy, в ) F ( a , в ) —

— K ++a ( a , в ) { K — ^— a ( a , в ) F ( a , в ) } _—a ,

F ( a , в ) = J J f ,& n ) • ^{+в y} ) d ^ d n . 0 0

По аналогии с изложенным выше подходом асимптотическое решение рассматриваемой контактной задачи для полуполосы берется в виде

q ^{( x} , у ) = q ,2 ^{( x} , у ) ⁺ q 22 ^{( x} , у ) — q 32 ^{( x} , у )■ ⁽¹³⁾

Внося в соотношение (13) выражения для решений уравнений (12) и произведя сокращения, в результате получим асимптотическое решение контактной задачи для полуполосы в виде

Для построения асимптотического решения о действии полуполосового штампа ширины 2 c при c >>  1 на анизотропную композитную слоистую среду, как и в случае полосового штампа, введем эталонное двумерное интегральное уравнение Винера - Хопфа, имеющее вид [28]

. те те

q ( x , у ) =       J J [ K -¹ Fe - ^{( a} x ^{+в y} ) —

—те —те

те те

^K q n = J J ^{k (} x n   ^y n , у п -n n ) q n ftn , n n ) ^d ^ n d n n = ^f„ ^{( x} n , у п )>

0 0

0 <  x n < те ,  0 <  у п < те ,

. тете qn (xn, уп) = -M f Qn (a, p)enу-)dadp, 4n —те —те

— 2 ^K 1 +в { ^K

— 2 k 2 —в { k 2^

— K J { к -; F} e - - ^{(a x 11 y} >  +¹

+a [ a j —a              2

+ ¹ K ₂— 1 { K₂

2    2 +a l 2 a

e —i ( a x +в ( у + c )) +

— i ( a x +p ( c—у )) _ - в ^e

—

_e-itm ⁺« у ^{+ c} »₊     (15)

e —- ( a x +в ( c — у ))

—a

. тете

k ( x n , у п ) = лМ   J K ( a , P ) e x ^{n уп} ’ d a d p ,

4n —те —те те те

F n ( a , p ) = J J f„ g n , n n ) e ^{- a n уп} ’ d ^ n d n n ,   n = 1,2,

0 0

+ 2< K 1 +u K 1 +u K 1 —a f } +a ! . ■

+ K 1 -в+a { K 1 -в-a { K 1 —в F } +в } —a ) e — ^{( a} x ^{+в ( y + c} » +

+ 2< K 2 —au K 2 -a-_P { K 2 —a F 2 } +a ь+

+ K 4+a { K 2 -в-a { K 2 —в F ! .. } —a ) e ^{+ c}—^y » ] d a d в + O ( c Л

Исследование решения контактной задачи для полуполосового штампа

Изучим роль каждого члена в представлении решения (15). Первый член в правой части решения (15), как и в (11), является вырожденной составляющей решения, к которой оно стремится при удалении от границ. Вторые члены функций под интегралом дают известную концентрацию контактных напряжений под прямолинейными боковыми границами штампа, как и в (11), опи- сываемую функциями (Jy + c) , (у]c - у) соответ- ственно. Новыми, по сравнению с (11), являются четвертый, пятый и шестой члены, описывающие концентрацию контактных напряжений q(x, y) функ- цией (4х)

под прямолинейной торцевой границей по- луполосового штампа. Показатели концентрации напряжений на прямолинейных участках одинаковые. Особый интерес представляют члены седьмой и восьмой, описывающие концентрацию контактных напряжений в нижней угловой точке границы штампа, а также девятый и десятый, дающие ее в верхней угловой точке. Ранее, в публикации [31], приближенным методом исследовалась концентрация контактных напряжений под клиновидным штампом при наличии его движения с кулоновским коэффициентом трения p << 1. Этот случай при от- сутствии трения отвечает варианту изотропного основания, а при наличии трения –анизотропному. Результат расчета концентрации контактных напряжений под клиновидным штампом на дается рис. 3, где е = (1 - 2v)(2 - 2v)-1 p , v - коэффициент Пуассона.

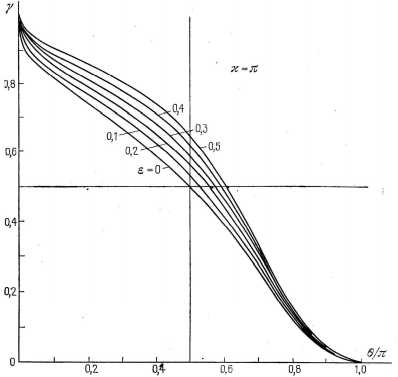
Рис. 3. Поведение параметра особенности Y в угловой точке штампа для разных коэффициентов Е , зависящих от коэффициента трения. Для сравнения с результатом статьи необходимо брать соответствующие значения е при 0/п = 0,25

Fig. 3. Behavior of feature parameter Y at the stamp corner point for different coefficients, depending on the friction coefficient. For comparison with the paper result, it is necessary to take the corresponding values of е when 0/п = 0,25

На рис. 3 приводятся графики особенностей в вершине клина для разных его растворов 2 0 , 0 < 0 < п , приближенно вычисленных в [31]. Чтобы сравнивать с прямым углом клина настоящей статьи, необходимо рассматривать случай 0/п = 0,25. При Е = 0 трение штампа с основанием отсутствует и задача становится изотропной. Для этого, более простого случая, ниже детально демонстрируется выявление особенности в угловой точке штампа. Оно потребовало выполнения впервые возникший в контактных задачах двойной факторизации функции двух переменных. Именно двойная факторизация функций позволяет выявлять концентрацию контактных напряжений в угловых точках штампа. В качестве примера для случая Е = 0 покажем правило формирования седьмого члена подынтегральной функции для q ( x , у ), когда функция K ( а , в ) обладает свойством (2) и имеет при больших а , в вид

K ( а , в ) = ( а ² + в ² + A ²) ^- 2 , A >  0.

Более сложные случаи функций K ( а , в ) факторизуются с помощью операторов (6).

При осуществлении факторизации по одному из параметров остальные находятся на вещественной оси. Факторизовав функцию K ( а , в ) по параметру а на верхнюю полуплоскость, получаем

1 _1         - 1

K _+а ( а , в ) = [ а + i ( в ² + A ²)² ]’ 2 = O ( а ²), A >  0.

Факторизацию функции K _+а ( а , в ) по параметру в на верхнюю комплексную полуплоскость можно выполнить точно, в интегральном виде, нормализовав K +а ( а , в ) по в на бесконечности. Для этого рассмотрим функцию, стремящуюся к единице при |в|^^ . Имеем

G ( а , в ) = 4i ( в ² + c ²) 4 K _+а ( а , в ) ^ 1, |вН~, c = const, отсюда

K +а+_р ( а , в ) = ( в + ic ) - ⁴ exp^ J ^G ( О , ~ d П , в^ П + .

2 п i Г 2 П-в

Тогда получаем оценку

• - 1         - 1

K +„+р ( а , в ) ^ C ( в + ic )“ = O (в’⁴), вь ~ .

Внося эти оценки в (15), асимптотически оценив интеграл, получим в результате несложного анализа для этого члена поведение вида

• - 3

q 0 ( x , у ) = O ( r ⁴ ), r = xx ² + у ².

Показатель степени близок к значению на рис. 3 при 0/п = 0,25 и Е = 0.

В анизотропном случае, е> 0, функция K ( а , в ) имеет вид

K ( а , в ) = ( а ² + в ² + A 2 ) ² [ 1 ± e sign a ] .

Двойная факторизация более сложная [29]. Она приводит к результату для разных e >  0 вида

- ³ - ¹³ °                      2           - 1

q ₀( x , y ) = O ( r 4 2 ), r = xx + у 0 = n arctg e .

Показатель близок к значениям на рис. 3 при 0/п = 0,25.

Таким образом, численный расчет подтверждает высокую точность асимптотического решения. В некоторых отраслях, где наличие угловой точки не принципиально, можно принимать штамп с закруглением. На закругленной границе по-прежнему будет оставаться концентрация контактных напряжений вида

( Jx ) . Од-

нако имеются отрасли, особенно связанные с созданием элементной базы электроники, при использовании сверхминиатюрных полосковых линии передач и в других областях, где пренебрегать угловыми точками нельзя, их необходимо исследовать [27; 31].

Несмотря на кажущуюся близость по формулировке интегральных уравнений (1) и (2), их решения качественно и количественно отличаются. Более того, они описываются разными формулами. Отсюда следует, что решением, полученным разделением пополам носителя решения для полосы, можно пользоваться для полуполосы только в дальней от торца зоне.

Заключение

Впервые полученное в статье асимптотическое решение контактной задачи для полуполосового штампа на анизотропном композите доступно для численного анализа, как один из подходов вычислительной механики. Для этого достаточно вычислять только интегралы (15), применяя стандартные пакеты программ вычисления интегралов, не прибегая к необходимости обращения систем уравнений. Вычисление контактных напряжений может быть выполнено для перечисленных во введении областей, в том числе при оценке сейсмичности в зоне перехода горной гряды в равнину.

Для исследования был обобщен асимптотический метод, развитый ранее для аналогичной контактной задачи для полосового в плане штампа большой относительной ширины. В работе впервые получено в аналитическом виде асимптотическое представление контактных напряжений под штампом, имеющим форму полуполосы. Впервые установлено важное свойство аддитивного присутствия в решении членов, описывающих концентрации контактных напряжений в разных зонах границы штампа. Это открывает возможность управления типами концентраций контактных напряжений в разных частях границы штампа, варьируя воздействиями на штамп. Оно позволило произвести сопоставление решений, полученных для полосового и полуполосового штампов. В результате показана ошибочность замены решения для полуполосового штампа частью решения для полосового штампа, получаемого делением носителя полосового штампа.