Асимптотическое решение гиперсингулярного граничного интегрального уравнения, моделирующего рассеяние плоских волн на интерфейсной полосовой трещине

ВЕСТНИК ПНИПУ. МЕХАНИКА № 2, 2019PNRPU MECHANICS BULLETIN

Материалы, используемые в промышленности или строительстве, могут содержать дефекты в виде микротрещин или микропустот, которые возникли либо на стадии производства, либо в процессе их эксплуатации. Наличие таких дефектов оказывает влияние на прочность или даже на целостность изготовленных из этих материалов конструкций. Для обнаружения внутренних дефектов достаточно эффективно используются методы ультразвукового неразрушающего контроля [1–7], реализация которых основывается на математических моделях, описывающих дифракцию и рассеяние волн на дефектах в упругом волноводе [3–5, 8–11]. Существуют различные подходы к построению решения задачи рассеяния упругих волн на трещинах, среди которых одним из наиболее широко применимых является метод граничных интегральных уравнений (МГИУ) [12–22]. Эффективность этого метода заключается в уменьшении размерности задачи, в возможности получения по-луаналитического решения, а в некоторых случаях и асимптотического решения [11, 20–27], а также в его высокой точности.

Контакт между материалами с разными упругими свойствами увеличивает вероятность формирования микротрещин [28]. При прохождении через волновод упругих волн свойства зондирующего сигнала различны для сплошной и трещиноватой среды [29–31], кроме того, упругие волны рассеиваются на границе раздела сред, представляющей собой, как правило, клеевые соединения [32, 33], что дополнительно усложняет идентификацию дефектов. При наличии зон концентрации микродефектов на границе раздела двух разнородных сред применяются граничные условия пружинного типа, которые моделируют поврежденный интерфейс [18– 23, 32–37]. Другой подход рассматривает поврежденный интерфейс как стохастически распределенный набор микродефектов, при использовании которого необходимо на первом этапе построить решение на одиночной трещине [10, 20, 21, 23].

При моделировании упругих тел с трещинами предполагается известным падающее поле и необходимо определить рассеянное на трещине поле. В рамках линейной теории упругости на концах трещин имеется сингулярность напряжений [16, 38]. В работах [3, 15, 16, 38, 39] получены граничные интегральные уравнения, которые в силу наличия особенности деформаций на концах трещины являются гиперсингулярными. Для получения решения ГИУ необходимо провести регуляризацию, одним из вариантов которой является выделение главной части ядра и далее применение численной схемы интегрирования [17, 40]. В методе Галеркина регуляризация гиперсингулярных ГИУ происходит автоматически в результате повторного интегрирования по берегам трещины [15, 18, 41]. При решении ГИУ методом Бубнова-Галеркина неизвестная функция раскрытия берегов трещины раскладывается в бесконечный ряд по ортогональным многочленам, выбор которых зависит от формы трещины. Например, полиномы Чебышева и Лежандра учитывают поведение решения в окрестности краев прямоугольной и круговой трещин соответственно. В том случае, если для ядра интегрального уравнения можно построить асимптотику, в результате чего интегральные уравнения решаются аналитически, то можно найти асимптотическое представление для скачка перемещений на трещине в частотном диапазоне, при котором характерный размер дефекта соизмерим с длиной падающей волны [20–23].

В настоящей работе рассматривается задача о рассеянии упругих волн полосовой трещиной, расположенной на границе раздела двух изотропных сред, обладающих разными упругими свойствами. В работе [8] решалась задача дифракции плоских волн на полосовой трещине в изотропном волноводе, а в работе [25] – в анизотропном волноводе, причем в обеих работах рассматривались волноводы, состоящие из одного материала. При нормальном угле падения задача распадается на антиплоскую [20] и плоскую [21], и при условии малых размеров трещины по сравнению с длиной падающих волн строится асимптотика функций раскрытия берегов одиночной полосовой трещины. Аналогичное квазистатическое, а также частотно-зависимое решение для круговой трещины, при построении которого также используется асимптотики ядра ГИУ, можно найти в работе [23]. В работах [21, 36] рассматриваются периодические массивы полосовых трещин, в работах [20, 21] – стохастически распределенные массивы полосовых трещин, с последующим определением коэффициентов пружинной жесткости, а в работе [42] – резонансные эффекты в слоистом периодическом композите с полосовой трещиной. В данной статье приводится зависящее от частоты асимптотическое решение для скачка перемещений на интерфейсной трещине, сходимость которого исследуется для случаев однородных и разнородных сред.

1.    Постановка задачи

Рассматривается рассеяние упругих волн на плоской полосовой трещине полуширины l , расположенной между двумя изотропными разнородными полупространствами V 1 и V 2 в плоскости z = 0. Ось Oz проходит через центр отслоения Q = { х | < l , | у| = 0} . Свойства сред, между которыми расположена трещина, определяются плотностью pj и константами Ляме

X j , ц j . Индекс j = 1 соответствует нижнему V 1 ( z <  0) и j = 2 верхнему V 2 ( z >  0) полупространствам.

Предполагается, что источник колебаний в безграничной среде достаточно удален от интерфейса и волновое поле, генерируемое этим источником, можно приближенно описать плоской волной, падающей под нормальным углом к интерфейсу. Рассматривается прохождение плоских продольной P и сдвиговых SV упругих волн из нижнего полупространства в верхнее с трещиной на границе раздела двух сред. Плоская волна частично проходит, а частично отражается интерфейсом и трещиной. Следовательно, волновое поле представляется суперпозицией поля в отсутствие трещины (в дальнейшем обозначается верхним индексом in ) и поля, рассеянного полосовой трещиной Ω (верхний индекс sc ). В рассматриваемом случае волновое поле без дефекта имеет вид

Р m ( e i k¹ m z + R m e - i k ¹ m z ) , z < 0,

P m T m e i k ² m z ,             z > 0,

τ ⁱⁿ

iclmk 1 mP m (eik1 mz - Rme-i ^ mz ), z < 0, .iC2mk 2mPmTmeik2mz,            z > 0, где Rm и Tm – коэффициенты отражения и прохождения; p – единичный вектор, определяющий направление распространения волны, а индекс m = {P, S} задает тип падающей волны: pP = (1, 0) при падении Р-волны и Ps =(0,1) для случая падающей SV-волны. Здесь параметрами cjр = Xj- + 2цj- и cjs = цj- обозначаются модули упругости, и соответствующие волновые числа связаны соотношениями

,  _ ® _ kj P =    = ®, vjP

p J

X J + 2ц J

1      ®       P j

и kj S = — = ®A — , vjS v цj где to - круговая частота; а VjP и VjS - скорости Ри SV-волн в полупространствах.

Отраженное и прошедшее волновое поле представляет собой суперпозицию продольных и поперечных волн и описывается двумерным вектором u = ( ux, uz). Заметим, что рассматриваются только гармонически установившиеся колебания и фактор e-itot, описывающий зависимость от времени, опускается из рассмотрения. На бесконечности перемещения и напряжения стремятся к нулю и выполняется условие излучения [13, 38]. В изотропном твердом теле уравнение движения при отсутствии объемных сил описывается уравнением Ламе k-2W-u - k-S2V(Vx u) + u = 0.         (1)

Граничное условие на интерфейсе при условии, что компоненты вектора напряжений т = { ст _xz , ст _zz } и вектора перемещений связаны законом Гука

( дu_y   дu_ ]           „ fд u_x   д u₇ )       дu₇

°xz = ц —- + —- , °ZZ=X\ —- + —- + 2ц —-, xz                               zz

V дz    дx J           V дx    дz J      дz имеет вид т=<°xz, ° zz )| z=0=( q\, q 2)■                (2)

Граничное условие на трещине чаще всего состоит в том, что трещина открытая, т.е. свободна от напряжений:

т 1 ( x ) = т ₂( x ) = 0,   z = 0, x g Q .         (3)

Иногда используются другие граничные условия, например, более общими граничными условиями являются граничные условия пружинного типа [19-23, 35], при которых все компоненты непрерывны и связаны соотношением т1 (x) = т2 (x) = к (u1 (x)-u2 (x)) ■

Здесь к - квадратная диагональная матрица в изотропном случае, вид элементов которой определяется типом и характером повреждения. При к = 0 условия вырождаются в граничные условия (3).

В работе используется условие (3) для описания рассеянного поля, которое характеризуется непрерывным напряжением и неизвестным скачком перемещений на трещине:

V = u ^c ,  | x | >  l ,

^c = т 2^c ,  | x | >  l ,                      (4)

^ < = т 2^c =- <, | x | <  l ■

• 2.    Построение граничного интегрального уравнения

Задача о плоских гармонических колебаниях u ( x , z , го ) в плоскости xOz упругого тела, неограниченного вдоль оси Ox , в рамках интегрального подхода [13] решается с помощью преобразования Фурье

U ( a, z , го ) = F_x [ u ( x , z ,

to го)] = J u(x, z, го) • eiaxdx ,

-to которое применяется к уравнению (1) и граничному условию (2). Тогда рассеянное поле может быть представлено в виде обратного преобразования Фурье

Fx" ( ^U )

u ^sc ( x , z ) =

to

J K 1 ( a, z ) Q ( a ) e ^{- i a x} da,   z < 0,

< ^- ”                                          (5)

to

J K ₂ ( a, z ) Q ( a ) e -^{a x} da,   z > 0,

^-to где Q (a) = Fx (тsc (x,0)) является Фурье-преобразованием напряжения на границе раздела сред. Построение Фурье-образа трехмерной матрицы Грина можно найти в [4], в двумерной постановке матрица имеет вид

K j ( a, z ) =

^Л M j ( a, z ) i P j ( a, z )^Л i S j ( a, z )    R j ( a, z )

где

M j ( a, ⁰ ) = ( - ¹ ) j ^{Yj j} , R j ( a, ⁰ ) = ( -1 ) ^j jj ,

P j ( ^a, ⁰ ) = £”( 2Y j ^{P 7} j ^s - ^{2 a 2 +} k 2^s ) ’

^Sj ( ^a , ⁰ ) = - ^Pj ( ^a , ⁰ ) ’ Y jm = 7^{a 2 - k}2j.

^A j =ц j

( ^{2 a 2 - k} 2s ) ^{- 4 a 2} Y j p у j s ■

Используя непрерывность перемещений между двумя полупространствами, можно выразить Фурье-преобразование напряжения на интерфейсе Q ( a ) через Фурье-преобразование A U ( a ) неизвестного скачка смещений A u ( x ) = u 1 ( x ) - u ₂ ( x ) на трещине:

Q ( a ) = L ( a ) A U ( a ),

L (a) = [ K i (a,0) - K ₂(a,0) ] ^{- 1} =f M ^{( a} )  i p ^{( a )} 1,  (7)

V iS (a)  R (a) J где M (a) =--R--, R(a) = —M—, P(a) = -S(a) = MR + PS      MR + PS

P

= - "MR—"PS , при пересчете M = M 1 ( a , 0) - M ₂ ( a , 0), P = P ( a ,0) - P 2 ( a ,0) и т.д. для всех остальных элементов матрицы.

Подстановка интегрального представления (5) для T ^sc в (4) с учетом формулы (7) дает следующее граничное интегральное уравнение :

—J L (a)A U (a)e^{- i a x} da = - т 1^п .

Г

Контур интегрирования Г почти всюду совпадает с вещественной осью, кроме полюсов функций ядра (7), где он отклоняется в комплексную плоскость в соответствии с принципом предельного поглощения [13]. Решение гиперсингулярного интегрального уравнения (8) ищется методом Бубнова-Галеркина, для чего компоненты вектора скачка перемещений A u = ( a u ^{( 1 )} , A u ^{( 2 )} ) раскладываются в ряд по базисным функциям с неизвестными коэффициентами разложения:

to

^{A u} m ^{( x} ) = X c mt P t ^{( x} )■               ⁽⁹⁾

t = 0

В качестве базисных функций выбираются полиномы Чебышева второго рода с весом, учитывающие геометрию трещины

P t ( x )= U t ( xl ) _; 1 - ( xl ) 2 •

( x + x ) t ^{+ 1} - ( x - v x ) t ^{+ 1}

U t ( x ) = "----------------—

2 V x ² -1

24 jm ^jm-4х

Y =a----— + O(a jm

2a

Используя эти аппроксимации, выводим асимптотические представления элементов Фурье-образа матрицы Грина (6)

.

Интегральные уравнения (8) проектируются на ту же систему ортогональных полиномов, а в результате дискретизации получается система

M(a) « m1 + -s^ю2,  R(a) « m1 + -sU to2, a  a3            a  a3

P (a) = - 5 (a) « m 3 + - s - ю ² , a a ³

где

где

N

S A tt ' ■ c t = g f                (^W)

t = 0

X 1 + 2ц     X 2 + 2ц

m1 = ^_ —7 ------у + — 7 ------у I,

² i ^ц 1 ^(X 1 ^{+ ц} 1 ) ^ц 2 ^(X 2 ^{+ ц} 2 ) J

^A tt' = ^ I ^{L ( a )} P ^{( a l} ) P * ^{( a} * ^{l )d a} ,   g t ' m

г

l

^- J ^T i m P t ' ( ^{x )d x} .

- 1

11        1                  1 I m 3 = -1---I,

2 ^X 1 + Ц 1 X 2 + Ц 2 J

1   ( ^Х 1 ^{+ 4 Х} 1 ^ц 1 ^{+ 5 ц} 1 ) ^р 1    ( ^X 2 ^{+ 4 Х} 2 ^ц 2 ^{+ 5 ц} 2 ) ^p 2

¹   8       ( X. +ш ) ² ц 2             ( Х.+ш, ) ² u. 2

P_t( a l ) = i t n ( k +1)

J_t + 1 ( a l ) a

• 3.    Асимптотика ядра интегрального уравнения

• 3.1.    Построение асимптотики ядра интегрального уравнения в бесконечно удаленных точках

Интегралы уравнения (7) имеют плохую сходимость на бесконечности [3], поскольку элементы L ( a ) растут как O ( a ) при a ^ да . Поэтому растущие как a и убывающие как a ^{- 1} на бесконечности элементы ядра выделяются в явном виде. Однако выделенные убывающие на бесконечности асимптотические слагаемые дают интегралы в системе (10), плохо сходящиеся в нуле. Поэтому для вычисления коэффициентов системы (10) область интегрирования разбивается на три области: ( -да , a ] , [ - a , a ] и ^ a , да ) . Соответственно, для ядра интегрального уравнения (7) строится асимптотика в окрестности нуля при a ^ 0 и в бесконечно удаленных точках при a ^ да .

При a ^ да для ядра интегрального уравнения L ( a ) справедливо следующее асимптотическое представление:

L ( a ) = L as + L ( a ),   I L ( a ) = O ( a^{- 5} ).       (11)

Для нахождения асимптотической матрицы L функции, входящие в элементы матрицы (6), выражаются через арифметические квадратные корни у j _m , которые раскладываются в ряд по а на бесконечности:

( ^X 1 ^{+ ц} 1 ) ^ц 1

^{( X} 2 ^{+ ц} 2 ) ^ц 2

1   ( 3^ 1 + 8Х 1 Ц 1 + 7ц² ) p 1    ( 3X 2 + 8^ 2 ^p 2 + 7^ 2 ) p 2

²   8       ( X.+ш ) ² Ц 2             ( Х.+ш. ) ²

( ^X 1 ^{+ ц} 1 ) ^ц 1

^{( X} 2 ^{+ ц} 2 ) ^ц 2

1   ( ^X 2 ^{+ 4 Х} 1 ^ц 1 ^{+ 5 ц} 2 ) ^p 1    ( ^X 2 ^{+ 4 Х} 2 ^ц 2 ^{+ 5 ц} 2 ) ^p 2

s. =                         -

^{( Х} 1 ⁺ Ц 1 ) Ц 1             ^{( X} 2 ⁺ Ц 2 ) Ц 2

,

,

.

Таким образом, для ядра (11) граничного интегрального уравнения (8) получается следующее асимптотическое представление в бесконечно удаленных точках (при а^да):

^L as

1г|.  +^ L =a asas

a ю2 (sgn(a) C1

a (

sgn(a) B 1     i B ₂   I

-iB2    sgn(a) B1 J i C2   | sgn(a) C3 J,

где

m ₁

B1      2     2, m1 - m 3

m ₃

B2 =   2     2, m 3 - m1

2 m 1 m 3 s 3 - m 2 s 1 - m 3 s ₂ 22²    ,

( ^m 3 ^{- m} 1 )

m 1 m 3 ( s 1 + s ₂) - s 3 ( m 2 + m 2 )

( m 2 ^- m 2 ) 2

C 3 =

2 m 1 m ₃ s ₃ - m 2 s ₂ - m 2 s 1

( m 2 ^- m 2 ) 2

.

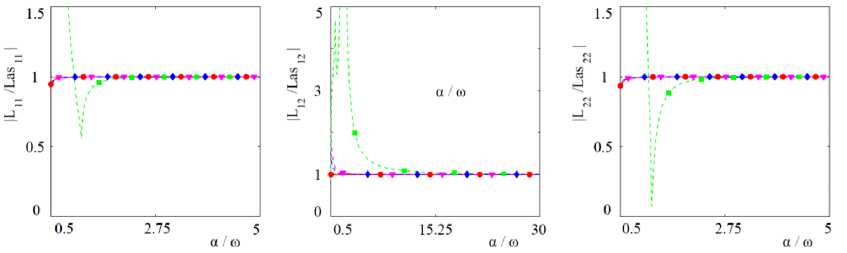
На рис. 1 изображен модуль отношений элементов асимптотического представления ядра, найденных по формуле (12), к элементам ядра (7) для разных пар ма-

териалов, значения параметров которых приведены в таблице. В качестве материала первого полупространства ( j = 1 ) выбран алюминий. Материалами второго полупространства ( j = 2 ) являются алюминий, сталь, свинец и оксид алюминия.

При нормировании параметра преобразования Фурье а на частоту to отношения элементов ядра интегрального уравнения (8) к элементам асимптотического ядра не зависят от частоты. Для пары алюминий

– алюминий демонстрируется наилучшая сходимость асимптотического представления ядра к исходному ядру интегрального уравнения. Можно заметить, что для любой пары материалов, начиная с некоторого нормированного значения параметра интегрирования а , все отношения стремятся к 1, что означает сходимость элементов асимптотического представления ядра (12) в бесконечно удаленных точках. Наиболее медленная сходимость наблюдается у пары алюминий – свинец .

а                                   б                                   в

Рис. 1. Модули отношений элементов матриц ядра L ( a ) и асимптотического представления ядра L^ в бесконечно

удаленных точках:     – алюминий;     – сталь;     – свинец;     – оксид алюминия

Fig. 1. The modules of the ratios between elements of the kernel L ( a ) and the asymptotic kernel L_m by points at infinity:

– aluminum;      – steel;      – lead;      – alumina

• 3.2.    Построение асимптотики ядра интегрального уравнения в окрестности нуля

При a ^ 0 матрица ядра имеет следующее асимптотическое представление:

L (a) = L 0 as + L 0(a, to),   ||L 0(a, to)||  = O (a⁵).  (13)

В этом случае арифметические корни у mj , входящие во все элементы матрицы (6), раскладываются в ряд по а в окрестности точки а = 0:

а ²        з

Y jm =^-i k jm ⁺ iT^— ⁺ O ^(a )

2 k_mj

Соответственно, элементы Фурье-образа матрицы Грина (6) имеют следующие представления при а ^ 0 :

M(а) » m01 + s0!^, R(а) » m02 + s02^, to      to3                  to      to3

P ( а ) = - 5 ( а ) « « + s ⁰³^, to ²        to ⁴

где

2 V1S  V1P   2 v 2S v 2 P m 03 =--- p1 v1P        p2 v 2P

1S ! v2S  7v2P  8v2S p2     2 v2P

„     ■ I ^V 1S ^{7 V} 1P ^{- 8 V} 1

^s 01 = ¹ I            z

( P 1      2 V 1P

• ⁸ v 25  ^V 1P _ ⁴ v ³ 5 ₊ ^{8 v} 2 5  ^v 2P _ ^{4 v 3} 5

_v    ^{2 V} 1P       ^V 2P ^p 1      ² v 2P       ^v 2P ^p 1

• ^V 2S  ² v p ^{+ 8 v} 1S    ^V 1S   ^v 12P ^- 11 ^v 12s

  ---⁺----

• v2P      p1       v1P      p1

• ^v 2S . ^{2 v} 2P ^{+ 8 v} 2S _ ^v 2S . ^v 2P ^{- 11 v} 2S

• V 2P       p 2        ^v 2P       p 2

В результате получается асимптотическое представление ядра (13) граничного интегрального уравнения (8) в окрестности нуля по α:

L0m = toL04) +aL0(2) + — L0(3) +^7 L0(4) = as          as          as             asas toto

B01   0 V  1  0

I + а I

• 0   B03 J    V-1B02

₊а2 1 c 01    0 lot I   0   1 c 02 )

+ to( 0   C03 J+to2 1-1C02

где

_  1         _   m 03a    R

B 01 =     ,  B02 =          ,  B03 = m 01          m 01 m 02

_ m 03   ^m 02 ⁵ 01

c01 =      2, m 01m 02

,       ^m 03 ^{( m} 023 - ^m 02 ⁵ 01 - ^m 01 ⁵ 02 ) + ^m 01 ^m 02 ⁵ 03

'02                                  22

^m 01 ^m 02

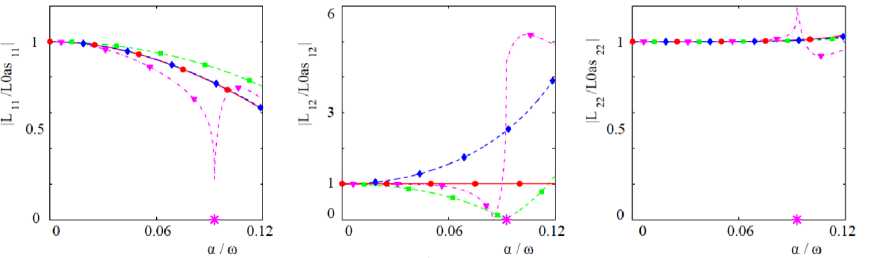
Для иллюстрации хорошего приближения к значениям ядра интегрального уравнения (7), полученным асимптотическим представлением (14), найдены модули отношений соответствующих элементов матриц (рис. 2). В окрестности нуля можно видеть равенство этих отношений 1 для всех пар материалов из таблицы. На горизонтальной оси a/ю звездочкой отмечены нормированное на частоту значение волнового числа Р- волны для оксида алюминия , которое является наименьшим из волновых чисел k _jm . В этих точках происходит резкое ухудшение сходимости асимптотики для пары алюминий – оксид алюминия .

_ m 03 - m 01 ⁵ 02

c 03 =          2    ■ m 01m 02

а                                 б                                 в

Рис. 2. Модули отношений элементов матриц ядра L ( a ) и асимптотического представления ядра L0_ai

в окрестности нуля:     – алюминий;     – сталь;     – свинец;     – оксид алюминия

Fig. 2. The modules ratio between elements of the kernel L(a) and the asymptotic kernel L01Z$ around zero point:      – aluminum;      – steel;      – lead;      – alumina

Упругие постоянные материалов

Material elastic constants

Материал	Постоянная Ляме, X 109 ГПа	Постоянная Ляме, p 109 ГПа	Плотность ρ, 103 кг/м3
Алюминий	51	26,3	2,70
Оксид алюминия	139,5	162,5	4,00
Свинец	36,32	8,4	1,61
Сталь	110,7	80,99	2,20

4.    Построение асимптотического решения гиперсингулярного уравнения

Матрица системы (10) раскладывается на сумму матриц, каждая из которых соответствует области интегрирования согласно введенному разбиению:

A „.= A t n^f + A t’ . ,                (15)

тотика ядра на бесконечности (12), а для вычисления A 0 асимптотика ядра в окрестности нуля (14). Рассматривается построение решения граничного интегрального уравнения (8) при условии t = t ' = 0, т.е. с использованием одной функции разложения p ₀ ( x ) ■ Фурье-преобразование полинома Чебышева нулевого порядка выражаются через функцию Бесселя первого порядка J_x ( x ) следующим образом:

Р0(аl) = l p0(x)elaxdx = nJl(al2. —i                    а

Матрицы системы (15) имеют следующие интегральные представления:

lnf

^A 00

2 L a ⁵  J

\_-да

J ² (a l ) a

да

fJ^a +J aа             z где элементы матрицы Aif выражаются через интегралы с областями интегрирования (-да; - a] и [а; да), а элементы матрицы A0t. - через интегралы по интервалу [—а; а]. При вычислении Atf используется асимп-

+™² L 2 J

J ² (a l ) /да J 1² (a l )

\ -да

a ³

a ³

a

da

A «, =П ™ L 0_S f J ^a+ L G ^;) ? J T <5 l lda + s                            s

2        J   a2            J a

L 0 (3) a               L 0 (4) a

+ — as- [ J 12 (a l )da +-- O- f aJ 12 (a l )da .

to J                m2  J

Для to^ 0 можно получить квазистатическое решение рассматриваемых ГИУ, которое совпадает с решением, найденным в [21]:

С учетом того, что матрица ядра L as четная по a

в элементах главной диагонали и нечетная по a в эле-

inf

A 00

^ A

КСт 00

- diag

ментах побочной диагонали, матрица A ⁱ ₀ ⁿ ₀ ^f после ана-

m1n

2       2,        22

2 1 m1    m3  I 21 m1    m3

литического вычисления интегралов в формуле получается диагональной:

A ⁱⁿf - I A 1

A 00 -I 0

A 1 -=B HG ( - a²1 ²) + ■ ^{n l} C ^f 2 - 8y + a²1 ² HG, (- a²1 ²1 - 8 in — Ito , 32 I                   ²V /       2 J

A 22 ^{-     HG} 1 ( ^{- a 2 1} 2 ) ⁺

+ kI C 3 ^f 2 -   + — ² 1 ² hg / — ² 1 ² j - 8 in — ^w ² ,

32 I                      2 ’         '        2 J

Матрица A ⁰ ₀₀ в квазистатическом случае при условии ak_jm бесконечно мала и не вносит существенного вклада в решение.

Подставив квазистатическое решение c ⁰ _{0 m} системы (10) в разложение (9) при условии t - 0, можно определить скачки перемещений, причем решения являются чисто мнимыми и для падающей Р -волны:

A u р^{С -} { 0, c 0p^p 0⁽ x ) } ^-

^{2i k} 1p k 2p ( m 3 ^{- m} 1 ) ^{( X} 1 ⁺ 2 ^ц 1 ⁾⁽X 2 ⁺ 2Ц 2 )^2---Г

,    m1 (k1P (X1 + 2Ц1 ) + k2P (X2 + 2ц2 ))               | , где у-0,577216 - постоянная Эйлера, а HG(z)- и для падающей SV-волны:

p ^F q ( ^{{ a} 1,'", ^a p ^} , ^{{ b} 1,"-, b q ^} , z )

– гипергеометрические

^А и К^{Ст -} { C 0S p 0⁽ x ), 0 } ^-

функции,

HG 1 ( z ) - i F 2 ( { 0.5 } , { 1,2 } , z ) , HG 2 ( z ) - 3 F . ( { 1,1, 2.5 } , { 2, 2, 3,4 } , z ) .

2ik1Sk2S (m32 - m12) Ц1Ц2 ^2  ^2  o m1 (k1sH1 + k2SЦ2 )              ’    .

При вычислении матрицы A ⁰ ₀₀ второе и четвертое слагаемые в формуле (16) обращаются в ноль и элемен-

ты матрицы также выражаются через гипергеометриче-

ские функции:

A 00 ^-

f A 01

I 0

⁰ J

A 02 J

При определении зависимых от частоты решений A u _m используется полное представление матрицы системы (15), учитывающее и асимптотику в окрестности нуля, и асимптотику в бесконечно удаленных точках; в результате решения c _{0 m} получаются комплекснозначными. В случае падающей Р -волны скачок перемещений имеет вид

2                     32

A 0    g ^—1 B .. hg / — 2 1 2 to + ^{n a} I C 01 hg  - — ² l ² ,

¹¹        4        ^Л       )       12to        4 V      /

^{A u} ЧЗ ^- { 0, ^C 0P Р 0⁽ x ) } ^-

2                      32

A ₂'₂ -       B ³ HG₃ - a ² 1 ² to + ™ ^l C ⁰³ HG. - a ² 1 ² ,

²²        4         ³                   12to        ⁴

где       HG 3 ( z ) - 1 F 2 ( { 0.5 } , { 2,3 } , z ) ,        HG . ( z ) -

- 2 F 3 ( { 1.5,1.5 } , { 2,2.5,3 } , z ) .

Правая часть системы (10) зависит от типа падающей волны. В случае падения Р-волны

in k _1P k _2P ( m ₃ ² - m 1² ) ( X 1 + 2ц 1 )( X₂ + 2ц₂ )

,   ( k 1P ( X 1 + 2Ц 1 ) + k 2P ( X 2 + 2Ц 2 ) ) ( A n + A 01 )

x 41 ² - x ² } ,

а в случае падающей SV -волны

^{А и} Ч^{З -} { ^C <0S ^p 0⁽ x ), 0 } ^-

_ _ i ⁽Х 1 ⁺ 2Ц 1 ) ⁽X 2 ⁺ 2 ^ц 2 ) k 1p k 2P ( X 1 + 2ц ) k 1p + ( X 2 + 2ц 2 ) k 2p

l n p P ,

-------^{in k 1S k 2sЦ1Ц 2} -------- 41 ² - X ² , 0 ^{( k} 1S ^ц 1 ^{+ k} 2S H ² ) ( A 22 ⁺ A 22 )

и в случае падения SV-волны

_   1 ц1 ц 2 k1S k2S I- g0S -      z ,     T lnps.

^ц 1 ^k 1s ^+ц 2 ^k 2S

На рис. 3 приведены отношения действительных и мнимых частей квазистатического решения, найденного в работе [21] и зависящего от частоты решения для пар материалов алюминий – алюминий и алюминий – оксид алюминия . Здесь и далее на рисунках за единицу

круговой частоты принимается значение 2π МГц. На низких частотах ( ш <  5) наблюдается очень хорошее совпадение решений, тогда как с ростом частоты погрешность квазистатического решения становится существенной.

5.    Сравнение численногои асимптотического решений

Частотно-зависимые решения (17) и (18) зависят от выбранного значения точки а , которая разделяет области интегрирования при вычислении элементов системы уравнений (10). Каждой области интегрирования соответствуют различные асимптотические представления интегрируемых функций. Поэтому выбор значения а может существенно повлиять на вычисление элементов матрицы системы.

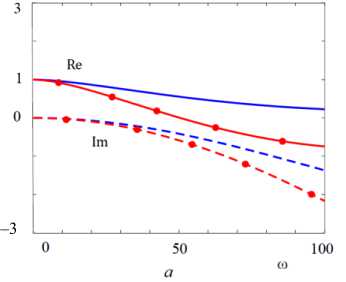
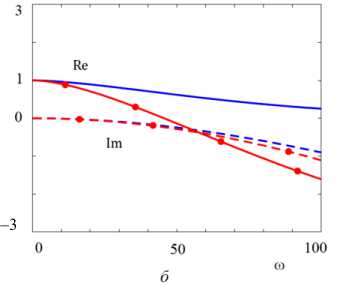
Рис. 3. Отношение действительных и мнимых частей квазистатического решения c ⁰ _{0 m} и частотно-зависимого решения c _{0 m} для пар материалов: а – алюминий – алюминий; б - алюминий - оксид алюминия: -- - Re ( c p c_P ) ;

-е- - Re ( с 0 /^c_s ) ;     - Im ( c p c p ) ; -• - - Im ( c ⁰/ c_s )

• Fig. 3.    The real and imaginary parts of the ratio between the quasistatic solution c ⁰ _{0 m} and the frequency-depended solution c _{0 m} for pair of materials: а – aluminum – aluminum;

  b – aluminum – alumina:

  
  

^Re ( c P / c p ) ; -•- ^{- Re} ( ^{c 0/} c s ) ;

- - Im ( c p c_P ) ;     - Im ( c p c s )

При определении значения а естественным оказывается стремление уменьшить расхождение между численным и асимптотическим решениями. Следует заметить, что численное решение включает в себя более одного члена разложения (9) и, соответственно, векторы численного и асимптотического решений системы (10) имеют разные размерности. Поэтому в качестве сравнения решений используется средний скачок перемещений, вычисляемый по формуле

1 ^l

A U m =     A u ( x )d x .

2 l     ^m

- 1

Поскольку J pt (x)dx = 0 при t > 1, вклад в средний скачок перемещений дает только коэффициент c при p(x). Соответственно, сравниваются асимптотическое решение c0 и численное решение c0 системы (10).

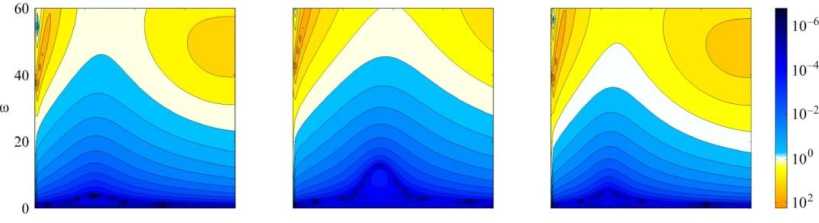
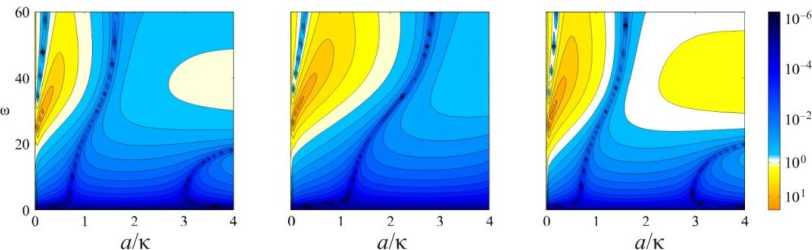
На рис. 4 построены для разных пар материалов поверхности абсолютной погрешности асимптотического решения, вычисляемой как модуль разности c и c . Анализ полученных результатов позволяет заключить, что для получения хорошо согласованного асимптотического решения необходимо правильно подобрать параметр а, оптимальное значение которого зависит от частоты. Параметр а может быть представлен в виде a = n к, где к - наименьшее из волновых чисел рас сматриваемой пары материалов. Значение п отложено по вертикальной оси. Выбор точки деления зависит от частоты, типа падающей волны и сочетания свойств материалов. Соответственно, для каждой пары материалов выбирается свой параметр п. Только в случае Р-волны для однородных материалов (алюминий – алюминий) и разнородных материалов (алюминий – оксид алюминия, алюминий – сталь) оптимальное значение точки а = пpk подбирается однозначно, поскольку наблюдаются практически вертикальные зоны минимумов. В случае S-волны выбор точки а = п к меняется с изменением частоты как для однородных, так и для разнородных материалов.

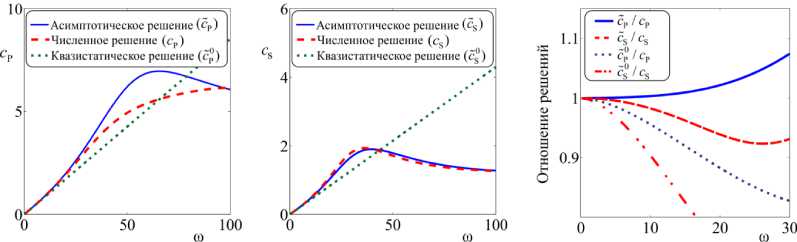
На рис. 5 показаны зависящее от частоты асимптотическое решение (сплошная линия), квазистатическое асимптотическое (точечная линия), а также численное решение (пунктирная линия) для пар материалов алюминий – алюминий и алюминий – оксид алюминия, причем лучшая согласованность наблюдается для S-волны, если выбрать параметр асимптотической модели Пs = 1,5 . В пределах 30 МГц расхождение численного c0  и асимптотического c0 решений для Р-волны и S-волны менее 10 %.

Аналогичные графики только для пары алюминий – оксид алюминий , полученные для параметров

Пp = 2, n5 = 1,7, изображены на рис. 6. Можно видеть, что погрешность, полученных асимптотических формул в частотном диапазоне до 30 МГц не превышает 5 %. На графики также нанесены линии, соответствующие квазистатическему решению С0m , иллюстрирующие хорошее качество аппроксимации на низких частотах. Графики отношения модулей решений асимптотических к численному наглядно демонстри- руют расширение диапазона применимости частотнозависимой асимптотики по сравнению с квазистатиче-ским приближением.

Построенные частотно-зависимые решения для скачков перемещений в дальнейшем могут быть использованы для получения частотно-зависимых коэффициентов пружинной жесткости (4) аналогично тому, как были найдены квазистатические коэффициенты пружинной жесткости в работах [21, 23].

а                               б                               в

г

д

Рис. 4. Абсолютная погрешность асимптотических формул в зависимости от частоты колебаний и параметра a для падающей P -волны ( а , б , в ) и S -волны ( г , д , е ), а также разных пар мaтериалов: алюминий–алюминий ( а , г ); алюминий–оксид алюминий ( б , д ) и алюминий–сталь ( в , е )

• Fig. 4.    The absolute accuracy of asymptotic formula depending on the frequency range to and the parameter a for the incident P -wave ( а , b , c ) and S -wave ( d , e , f ) for the various pairs of materials: aluminum–aluminum ( а , d ), aluminum–alumina ( b , e ) and aluminum–steel ( c , f )

  

  б

  а

  Рис. 5. Сравнение модулей решений численного и асимптотических: квазистатического и частотно-зависимого для пары алюминий-алюминий при n _P =n S = 1,5 : а - для P- волны; б - для 5- волны:   - асимптотическое решение; - - - численное решение;

  
  

... - квазистатическое решение, и в - отношение модулей решений: __ - | c _P |/| c _P | ; __ - | c _S |/| с ₅ |;  ... - c P /| c_P | ; _.. - c S /| cs|

• Fig. 5.    Comparison of modules of the numerical solution, the quasistatic asymptotic solution and frequency dependent asymptotic solution for pair aluminum-aluminum and p_P =n = 1,5 : a - for P- wave; b - for 5- wave:  - asymptotic solution; - - - numerical solution;

... - quasistatic solution, and c - relations of modules solutions: __ - | c _P | / | c _P | ; -- - | c _S | / | c _S |; ... - cP / | c_P | ; -.. - cS / | c_S|

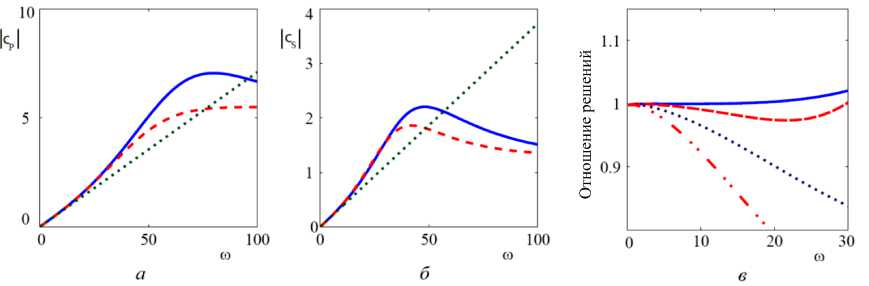
Рис. 6. Сравнение модулей решений численного и асимптотических: квазистатического и частотно-зависимого для пары алюминий-оксид алюминия при Цр = 2, П = 1,7 ^: а — Для P- волны; б — Для S - волны:   - асимптотическое решение; - - - численное решение; - квазистатическое решение; в - отношение модулей решений: __ - | с _Р |/| с _Р | ;  --  - | c _s |/| c _s |;

^- c P p| с_р | ^{;     -} c S p cs|

• Fig. 6.    Comparison of modules of the numerical solution, the quasistatic asymptotic solution and frequency dependent asymptotic solution for pair aluminum-alumina and n _p = 2, n _s = 1,7 : a - for P- wave; b - for S- wave: __- asymptotic solution; - - - numerical solution;

  I c S p c s I

  
  

... - quasistatic solution; c - relations of modules solutions:__ - | c _P | / | c _P | ;      - | c _S | / | c _S |;     - c p / | c_P | ;     -

Заключение

В настоящей работе рассматривалась задача рассеяния упругих волн полосовой трещиной, расположенной на границе раздела двух сред c разными упругими свойствами. Дифракция волн на одиночном дефекте описывается граничным интегральным уравнением. Построенная частотно-зависимая асимптотика ядра ГИУ для бесконечно удаленных точек параметра преобразования Фурье совпадает с решением, приведенным в [21] для квазистатического случая, что дает полное соответствие между решениями на низких частотах. При больших значениях угловой частоты существенный вклад в решение дает также асимптотика ядра ГИУ в нуле. Сравнение построенного в этой работе асимптотического решения с численным показало хорошую согласованность для более широкого диапазона частот, чем в случае ранее полученного квазистатического решения. Найденные частотно-зависимые средние скачки перемещений на полосовой трещине могут быть использованы для определения частотно-зависящих пружинных