Асимптотика распределения числа восстановлении в процессе восстановления порядка (k 1, k 2)

В теории надежности процессом восстановления называется последовательность взаимно независимых неотрицательных случайных величин X i с функциями распределения F i (t ), i = 1,2, — [1,2]. Для восстанавливаемых элементов процесс восстановления моделирует ситуацию, когда после первого отказа ( X 1 – наработка элемента от начала работы ( t = 0) до первого отказа) элемент восстанавливается или заменяется и работает до следующего отказа ( X 2 – наработка элемента от первого до второго отказа), затем он восстанавливается или заменяется и работает до следующего отказа и т. д. Время восстановления не учитывается. Считается, что оно пренебрежимо мало по сравнению со временем наработки элемента между отказами.

Существуют различные модели процессов восстановления, отличающиеся разными предположениями относительно функций распределения F i ( t ) случайных величин X i . Основной моделью, которая рассматривается в математической теории надежности, является простой процесс восстановления, для которого

F( t ) = f ( t ), i = 2,3, — .

Процесс восстановления называется общим ( запаздывающим ), если F ( t ) = F ₂ ( t ), i = 3,4, — .

В данной статье мы будем рассматривать процесс восстановления порядка ( k 1 , k 2 ). В этом процессе функции распределения удовлетворяют условию [3; 4]:

F i (t ) = F j ( t ) при i = j (mod k 2 ), i , j >  k -

Последовательность функций распределения для данного процесса имеет вид

^F i , ^F 2 , ^— , FM,

Fk i , F k 2 +1 , ^— , F k i + k 2 -1 , F k i , F k 2 +1 , ^— , F k i + k 2 -1 , ^— , 'V' 'V '

где функции распределения F k _i , F k 2 _+b — , F + _k 2 - образуют повторяющуюся (периодическую) часть рассматриваемого процесса восстановления.

Процессы восстановления порядка (1, 1), (2, 1) (в первом случае F (t) = Fi (t), во втором -F (t) = F2 (t), i = 2, 3, —) соответствуют простому и общему (запаздывающему) процессам восстановления. Эти случаи хорошо изучены, особенно в том, что касается асимптотического поведения их различных характеристик [1; 2].

Пусть N(t) – случайное число отказов (восстанов- k лений) за время от нуля до t и Tk = Z Xi, k > 1 -i=i моменты отказов (восстановлений). Тогда

P ( N ( t ) >  k ) = P(T k <  t ).              (1)

Для асимптотического распределения N(t) про- цесса восстановления порядка (2, 1) (общего процесса) имеет место теорема [2]: пусть случайные величи- ны X1 , X2 имеют конечные дисперсии

22 σ 12 и σ 22 .

Тогда limP t ^л

( t

N (t) - — g2 TtP?

= Ф ( X ), Ф ( X ) = ^

2π

x - tl j e ² dt ,

-Л

< X

где ц2 = M(X2), здесь M(Xi) - математическое ожи- дание случайной величины Xi.

Рассмотрим аналог этой теоремы для процесса восстановления порядка ( k 1 , k 2 ).

Введем следующие обозначения: Yi = Xki + i-i, k2

i = 1,2, -, M(Yi) = Mi, D(Yi) = Di= g2, D = £Di, i=1

k ₂

A = Z M i - i =i

Для последовательности одинаково распределенных случайных величин имеет место центральная предельная теорема [5]: если независимые случайные величины ^i, ^2, _, ^n, — одинаково распределены и имеют конечную отличную от нуля дисперсию, то при n ^л равномерно по x

[                            1 X - t 2

P 1Z (^ k - M k )) <  X ' V J e ² dt ,

B-                        2n l_ n k =1                          J -Л

n где Bn = ZD(Zk)-

V k =1

Докажем аналог этой теоремы для процесса восстановления порядка (1, k 2 ).

Теорема 1. Пусть случайные величины Y i , задающие процесс восстановления порядка (1, k 2 ), имеют конечные дисперсии d , = о², i = 1, 2, ..., k 2 , хотя бы одна из которых отлична от нуля. Тогда равномерно по x

Z ( Y - M (Y ))

lim P k ^да

k

Z Di i=1

< x

= Ф ( x ).

Учитывая, что интегралы в правой части последнего равенства стремятся к нулю при n ^ да (в силу предположения о конечности дисперсий D i ) и lim p_n = да , получим равенство (2). n ^да

Теорема 2. Пусть случайные величины X i имеют конечные дисперсии, хотя бы одна из которых при k 1 <  i <  k 1 + k ₂ отлична от нуля. Тогда в процессе восстановления порядка ( k 1 , k 2 )

Д о к а з а т е л ь с т в о. При сделанных предположениях достаточно проверить, что выполняется условие Линдеберга: при любом т >  0

n lim^"Z L м    (x-Mk)2dFk(x) = 0. (2)

n^x В 1Л Jx-Mk|>тBn n k=1

lim P t ^»

N ( t ) - kA t

k ₂ V DtA - 3

< x = Ф ( x ).

n

Действительно, пусть B n = I D Z Y i , n = P n k ₂ + q_n ,

V i =1

где q n - остаток от деления n на k ₂ ( q n <  k ₂). Тогда

Д о к а з а т е л ь с т в о. Очевидно, что функции распределения F ( t ), i = 1, ^ , k 1 - 1 не влияют на асимптотическое распределение случайной величины N ( t ). Запишем k в виде k = m_kk ₂ + q_k , где q_k - остаток от деления k на k 2 . Тогда

k

k

qk

M\ Z Y i l = Z M(Y i ) = mA + Z M i

k

k

i =1

qk

n

qn

B n = a D Z Y =A P n D ⁺ Z D i . При ⁿ >  ^k 2

D I Z Y i l = Z D ( Y ) = m k D + Z D i V i =1 7 i =1                           i =1

= ^{k -} q k k ₂

_ ^{k -} q k

qk

A + Z M i , i =1

qk

D +

k

k

n

Z J   (x - Mk )2 dFk (x) = k =1 Bn Ix-MkI>TBn

Z ( Y - m ( Y i ))   Z Y i

-

^{k -} q k

k ₂

qn

p_nD + Z D i L ^{I x - M} 1 > ^т B n

J     ( x - M 1 ) 2 dF₁( x ) + ... +

k

Z Di i=1

Обозначим

^{k -} q k

k 2

i =1

⁺ J     ^{( x -} M k ₂ ^{) 2 dF} k ₂ ^{( x} ) ⁺ ... ⁺

I x - M k ₂I >t B n

Z k =

k

Z Y i

^{k -} q k k ₂

+ J    ( x - M n )² dF n ( x ) =

| x - M n I>T B n                        _

qn

P ⁺ Z d ,

i =1

⁺ P n

P n    J ⁽ x ^{- M} 1 ) 2 d^F 1⁽ x ) ⁺ ... ⁺

I x - M 1I > t B n

J     ( x - M k 2 )² dF k 2 ( x ) +

I x - M k ₂I>T B n

+ Z J   (x - Mk )2 dFk (x) = k=1 Ix - MkI>TBn                        _

q n

___Z D L l x - M 1 I>T B , P n i =1 ⁱ

J     ( x - M ₁)² dF₁( x ) + ... +

n

+ J     ( x - M k 2 )² dF k ₂ ( x ) +

I x - M k ₂ I > t B n

1 J qn,

+— Z J ^{( x - M} k ) ^dF k ⁽ x ). ^{Pn k} =1 I x - M k I>T B n                      _

k ₂

qk

A -Z Mi i=1

qk

D +Z Di i=1

qk

A - Z M i

qk k-q k D + Z D , ^k 2           i =1

.

Z D i , i =1

.

По теореме 1 имеем lim P(Zk < t) = Ф(t).

k ^да

Рассмотрим P ( N ( t ) >  k ):

N ( t )

P ( N ( t ) >  k ) = P

t

tk 2 _k A

^tk 2 '

t

.

Учитывая (1), получим f J^     ^

P ( N ( t ) >  k ) = p \Z Y i <  t l =

V i =1         7

f k

Z Y i

= P

k - qk _л qk?

-^k A -Z Mi k2         i=1

k - qk ^k

V v k 2

qk

D + Z Di i=1

<

k - q,    qL tkkAA -Z M, i k 2 i=1

qk k-qk D + yD, i k 2           i=1

A

= P

Z k <

kA qA k t--+ —--> M, i k 2 k 2 i=1

k qk k - qk+ d !Zi d,

.

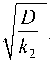
Следуя доказательству теоремы об асимптотическом поведении распределения N ( t ) для общего процесса восстановления [2; 6], рассмотрим при фиксированном t последовательность { z k }, определяемую

равенством

k = ^2₊ tz_z .

A ^k

Из (5) и (6) получим

-A - q k A + vM,

i

= P Zk s

^k 2        ^k 2 i =1

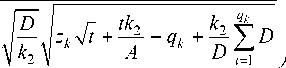
Предполагая, что lim z_k = z , из (4) имеем k ^x

lim P t ^«1

N ( t ) - A

t

= 1 -Ф

zA

= 1 -Ф

k ₂

z A ³ k ₂ D

.

Обозначив x =---,= к окончательно получим k2 D

tk

N ( t ) 2 lim P ---; ---A t ^” k 2 ^tD.A ^- 3

> x = 1 -Ф ( x ).

Отсюда следует равенство (3).

Таким образом, для процесса восстановления порядка ( k 1 , k 2 ), обобщающего известные в теории надежности простой и общий процессы восстановления, имеет место сходимость распределения числа восстановлений в момент времени t к нормальному распределению M ( N ( t ) ) = -^2 1 и о ( N ( t ) ) = k2 ^tDA ^{- 3} . Этот результат можно использовать, например, для расчета необходимого на данный период времени числа запасных элементов при эксплуатации технических систем.