Асимптотика затопленной струи и процессы переноса в ней

Затопленная (в том числе закрученная) струя несжимаемой жидкости благодаря малому числу определяющих параметров является, с одной стороны, классическим объектом теоретического исследования автомодельных асимптотических решений [1-5]. С другой стороны, она. представляет интерес для проведения теоретических исследований и модельных экспериментов, будучи «исходным фоном», на котором происходят различные физические явления [например, 6]. Практические применения многочисленны — форсунки двигателей, струйно-вихревые следы летательных аппаратов, нанесение покрытий, тестирование программ численного исследования сложных газодинамических потоков [например, 7-9]. Струйные потоки в затопленном пространстве изучены многими исследователями, но, поскольку подобные течения используются во многих отраслях техники и технологии, значимость их исследования не утратила, силу и по сей день.

Динамика, свободной струи, истекающей в затопленное пространство, математически строго впервые рассмотрена в работе [1], где найдены параметры потока в первом приближении. Следующее приближение получено в [2]. В настоящей статье исследована, газодинамика. струи в третьем приближении, а. также рассмотрен перенос тепла, и взвешенных частиц. Кроме того, исследована, турбулентная струя и проведено сравнение полученных аналитических результатов с классическими работами.

Следуя работам [1], используем сферическую систему координат г, Ө, ф. Решение системы уравнений Навье-Стокса. ищем в виде разложения по отрицательным степеням радиуса. г. Первые два приближения для компонент скорости и давления имеют вид

Vr = 1 Ғ (Ө) + 4 Ғо(Ө), Ve = 1 / (Ө), p =4 тт(Ө) + 4 ^о(Ө),(1)

г г^            г          гг где

I (Ө) = - '

A — cos Ө

Ғ (Ө) = 2ю [ ^A 2 - ¹₂ — 11 ,

(A — cos Ө)2

Ғо (Ө) = vp 1

-

3 (А2 — 1)      2(А2 — 1)2

(А — cos Ө)2   А(А — cos Ө)3

,

А cos Ө — 1 л (Ө) = 4 pv ²------------₅,

V ’         (А — cos Ө)2

ло (Ө) = 2vFo (Ө).

Здесь v — кинематическая вязкость, А — безразмерная постоянная интегрирования, которая находится из интегрального соотношения для полного потока, импульса:

T

I = 2 л J П_гг г² cos Ө sin Ө dӨ.

Величина Пгг равна

П..

4pv2 г2

J (А2 - 1)

( (А — cos Ө ) 4

-

А

А — cos Ө

} ■

Интегрируя, получим известное выражение [1]

i- -Д

-А ln -А+  .

А — 1

Третве приближение будем искать в виде

V = 1F (Ө) ₊ 1Ғо(Ө) + 4ғі(Ө), г г^         г

V g = 1/ (Ө) + 4/і(Ө), г г р = г2^{л(Ө) +} г3^о^{(Ө) +} г4лі^(Ө).

Уравнения Навье-Стокса в сферических координатах имеют вид

	VдV: + Vg дқ. — V2+ 1 др = т дг г дӨ    г р дг
v^	^ / 2 д% \ +   1  2 Ln Өдқ. \ — ж —   2 дг     дг     г2 sin Ө дӨ       дӨ /    г2    г2 sin	- — (И? ӨдӨ ( g	sin Ө)j ,
	VM , Vg М, VVg , £ др =			(3)
	дг    г дӨ     г    гр дӨ
= v	11 £ ( 2 д^ \ +   1  £ / . ӨдV9\ + £ дК _ [ г2 дг \ дг     г2 sin Ө дӨ \     дӨ     г2 дӨ	Vg	1
		г2 sin2	Ө ’

д

(sin ӨV_g ) = 0.

г sin Ө дӨ

1 д(г² V) г²    дг

Для удобства введем переменную t = А — cos Ө и вспомогательную функцию

^1 sin Ө"

В новой переменной известные функции имеют вид sin2Ө = 1 — А2 + 2А€ — t2, /(Ө) sin Ө = 2 v

А2

-

€2

--2А +t^ ,

Ғ (t) = 2 v (

А2

-

t2

1  3 ™-.І1 ";"."; — "21.

После подстановки выражений (1) и (2) в (3) будем иметь систему обыкновенных дифференциальных уравнений.

Из уравнения неразрывности системы (3) получим следующую связь между неизвестными функциями:

Fi(t) = (sin2Ө01(t))‘, где штрих обозначает производную по новой переменной t. Подставляя все эти выражения в уравнения движения системы (3), получим систему обыкновенных дифференциальных уравнений:

4TTi(t) = -2Fi(t) (2F(t) + 1) + /(Ө) sinӨ (F(t) - 20i (t)) + +•1 (t) F‘(t) sin2Ө - (F‘(t) sin2Ө)‘ - 2 F02(t),

7T1(t) = j 201 (t(F(t) + 3) dt + 3F1(t) - 01 (t)/(Ө) sin Ө.

Ее решение будем искать в виде

•1^(t) = ^{а +} »2 ⁺ »3 •

Учтем следующие соотношения:

sin²Ө = 1 - cos²Ө = 1 - A² + 2 а» - t²,

.    .      ( А2

/ sin Ө = v (2 —

-

t

F2 _  2,о2 Г4 (А2 - 1)4

F = " 0 Г AV

- 12

(А2 - 1)3

At5

+ 9

- - 4А + 2t), (А² - 1)² ₊₄(А2_12

-

б'’;1!

После подстановки этих выражений уравнений:

В

систему (5) получим алгебраическую систему

18 (А2

-

1) а + 6 b = 0,

-12 А (А2 - 1)2 а + 4ab = -6v02 (А2

-

1) ,

3.    Перенос циркуляции в струйном потоке

Большой практический интерес представляет закрученная струя, которая используется, например, в камерах смешения и сгорания топлив [7]. В данном параграфе рассматривается распространение циркуляции закрученного потока, в затопленном пространстве. Для этого рассмотрим уравнение Навье-Стокса для осесимметричного случая:

_VdV p + Vo dV_v + ^г dr r дӨ

V v.  Vo v.   ~_v \ d ( 2 dvA I d / sv.\ r + r cg r2 dr V dr J + sin Ө дӨ Vin6 ЭӨ )

-

V.

sin2 Ө .

8(А² - 1)² с = 4v0²

(А2 - 1)4

А2

•

Решение, удовлетворяющее данным уравнениям,

имеет вид

02    ,      302(А2 - 1)

а = 4А,   = -    4А ,

02(А2 - 1)2

^С =     2 А²

•

Таким образом, искомая функция равна.

0 ²

• ' = 4А

-

302(А2 - 1)

4At2    +

02(А2 - 1)2

2A2t3

•

Через данную функцию найдем искомые неизвестные в

исходных параметрах:

F1 = v02

2 [     (^А2 - 1)²

^{31 V0} 2А²(А - cos Ө)³

■ 3   (А2 - 1)3

2 А2(А - cos Ө)4

-

3   А2

-

-

4 А(А - cos Ө)2

7  (А2 - 1)2

2 А(А - cos Ө)3

+ 4А

] sin Ө,

(4А2 - 1)(А2 - 1) cosӨ

+ 2А2(А - cos Ө)2 + 2А

•

Введя циркуляцию Г = V . r sin Ө, преобразуем это уравнение к виду

V d ( r²V Г)

r²    dr

+     I" (VГ sin Ө) = v [I2! + 4S r sin Ө dr                 dr2   r2 дӨ2

-

ctg Ө д Г 1 r² дӨ

Решение данного уравнения будем искать в виде

Г = G + G. rr

Подставляя в (6) выражение для компонент скоростей в виде

Ғ (Ө)    Ғо(Ө)f(Ө)

V-г =--1--,,    vg = , r r^

получим уравнения для искомых неизвестных

I- ( fG sin Ө) = v 2 2G sin Ө + sin 6^ дӨ                              дӨ²

—FGo — FoG +    d(f sinӨGo) = v <6Go + sin Ө дӨ

-

й ⁹G\ cos ^Өм) ,

d ²Go дӨ²

dG\

^{— ctg 6} ее).

Записывая правую часть первого уравнения (7) в виде

4 ( fG sin Ө) = v 2 2 G sin Ө + sin6^4 дӨ                              дӨ²

-

cos Ө^ = v (sinӨ^і — 2Gcos ө) , дӨ           дӨ

после интегрирования получим

G = v (G‘ — 2 G ctgӨ) + const.

Постоянная интегрирования равна нулю, т.к. V . ^ 0 пр и Ө ^ 0, следовательно, G G „

= °(Ө)

чего

при Ө ^ 0 и G’ = —. Полученное уравнение интегрируется вторично, в результате Ө получим искомую неизвестную:

_G =     sin² Ө

^ (A — cos Ө)².

Постоянную интегрирования у находим из условия сохранения удельного момента импульса потока Lo на срезе форсунки:

7Т

2л У Ғ (Ө)G(Ө) sin Ө4Ө.

Проведя интегрирование, получим соотношение

^Lo =8 *^vl [зд^⁺²

ДА ^А + ¹! — A ln        .

А — 1

Для решения второго уравнения системы (7), как и в предыдущем параграфе, введем переменную t = А — cos Ө. Тогда уравнение запишется в виде

FGo — Fo G + (f sin Ө Go ) = v (6 Go + sin²Ө G^ ) .

После подстановки сюда известных функций (4), получим

/ А2 — 1 X _   , А2 — 1

^—2 (² 12^{- + 1}) ^{Go + (2}   ■

— 4А + 2t)G0 + (А² — 1 — 2 At +t²) G0

F0G0

v

где

FoGo = v_A^[—2 ^   + А^ — ₂ <^4A 2 ^— W ^— D +2 А2Д +2 ^А — 1] .

Решение последнего уравнения ищем в виде

Go =  +  + 7 + d + et t3 t2 t и находим неизвестные коэффициенты а = —Зу(А2 — 1)2 , b = 5^7 (А2 — 1), с = —Зу3А2 — 1, d = — 37, е = 37.

А            2             ,               2А ,          2 ,2А

В резулвтате

(А2 — 1)2   5 А2 — 1   3А2 — 1   1

^Go = ^Зу AdT" ⁺ 2 "12     2А1" — 2 ⁺ 2А =

_ Зу sin2 Ө [    1            А           А2 — 1

2А     А — cos Ө ⁺ (А — созӨ)^{3   2} (А — cos Ө)^{3 .}

Таким образом, искомая азимутальная скорость равна.

sin Ө Зу sin Ө [    1             А           А² — 1 ]

^ ⁷г²(А — cosӨ)^{2 А} 2г³А |_А — cos Ө (А — созӨ)³    (А — cosӨ)³]

• 4.    Перенос тепла и взвешенного вещества в струе

Рассмотрим теперь по аналогии с предыдущими параграфами перенос тепла, или вещества. в струе. Данная задача, также имеет большое практическое значение в технике и технологии [7-9]. Пренебрежем такими эффектами, как термодиффузия и конвекция, т.е. рассмотрим классическую задачу переноса, тепла, и вещества. Поскольку уравнения переноса тепла и концентрации аналогичны, достаточно исследовать, например, задачу о распространении веществ в затопленной струе. Пусть S — концентрация взвешенного вещества в струе, тогда его распространение описывается уравнением yas ц, as = D ц э(2 дз\     1        ӨдS^l т dr А г ЭӨ |_г2 Эг \ Эг ) А г2 sin Ө ЭӨ у ЭӨ

Будем искать его решение в виде

S = C + C -

v = F + F» г г

V - f Vg = - г

Как и в предыдущих параграфах, введем переменную t. В результате вместо исходного уравнения переноса, получим два. обыкновенных дифференциальных уравнения:

1(1 — а ² + 2 At — t² ) C‘ + [2А(1 + -^) — t(^ + 1) — ^А2-^] С' + (^А2-—^ — 1)с = 0, 2Sc                                  2Sc Sc           t              t² J

(1 — A² + 2 At — t²)Co + ^2A(1 + 2Sc) — (1 + Sc)t — 2Sc ^A 2 ~ ¹ ] Co +

+ 2(1 — 2 Sc) + 4Sc A2_t~ ¹ Co = —ScFoC.

Здесь Sc = — — число Шмидта. Решение первого уравнения системы (8) будем искать в виде

С = Ко t^m.

Подстановка, данного выражения в первое уравнение дает т = —2 Sc.

Следовательно,

Г = ^К

С    t2Sc.

Постоянная интегрирования Ко находится из интегрального соотношения для заданного потока вещества

7Т

J = 2 7Г У V_T С sin 6d6.

Подставляя полученный результат во второе уравнение системы (8), его правую часть получим в виде

-S сҒо С = — ^^ 1

t2be

-

3(A2 — 1)

t2

2 (A² — 1)2 1

⁺ At ] .

Для решения второго уравнения (8) сделаем замену неизвестного:

^С0    t2 ^sс.

После несложных выкладок получим уравнение

(1 — A² + 2At — t²) t² Y‘‘ + 2 [Sc(A² — 1) — A(2Sc — 1) t + (Sc — 1)t²] tY ‘ +

[........ ')'2Д"‘|.

+2 [Sc (A2 — 1) — (Sc — 1) t2] Y = —Sc 3 Ко решение которого находим в виде

Y = at + b + -.

Подстановка, этого выражения в последнее уравнение позволяет найти искомые коэффициенты, так что

„   вК₀ Г2Sс — 11 — 4Sc A² — 1 1

Со =                ■    '        2      '     ’          ■

С учетом (5) выпишем найденные решения в сферических координатах:

S =----- ^К ( 1 + ³ Г ^2S* — ¹ (A — cos0) + 1 — ^4SC +    ^A 2 — ¹ Sell .    (9)

г (A — cos 0)^2Sc I г     2 A ^v         ’      2        A (A — cos 0)

Аналогично можно записать и выражение для температуры, заменив Sc на Pr, а Ко — на Мо — постоянную интегрирования, которая находится из условия сохранения потока тепла (Pr — число Прандтля).

5.    Анализ полученных результатов

Таким образом, получены точные решения уравнений Навье-Стокса до третвего члена, разложения по радиусу г, а также для переноса циркуляции, тепла и концентрации до второго члена. Эти решения верны для ламинарной струи. Однако здесв возникает известный парадокс нулевого расхода:

7Т

7T j Ғo(ө)dө = o.

Qo = lim27rpr² / !ф sin Ө йӨ = 2 ттр r^0

Здесв Qo — секундный расход массы из трубки, р — плотность газа, которую будем считать постоянной. Полученный результат объясняется тем, что в реальности от 0 до некоторого угла Ө* реализуется турбулентное течение, а вне этой области течение можно считать потенциальным. Однако, как показано, например, в [3], для осесимметричной турбулентной струи ее вязкость можно считать постоянной. Следовательно, полученные результаты можно применить и для турбулентной струи, только во всех интегральных соотношениях интегрирование нужно провести от 0 до Ө*, т.е. потенциальным движением вне турбулентной зоны нужно пренебречь. Тогда, из выражения (10) получим

ө *

Qo = 2 ^р [ Ғо(Ө) йӨ = -2 ^v3p sin² Ө* ¹ . ^ ^cos * = ^pUoR2.

(И)

A (A - cos Ө*)²

о

Здесь Uq — скорость истечения потока из трубки, Ro — радиус трубки. Отметим, что для турбулентной струи выполняется условие I/pv² >>  1. В этом предельном случае (так называемой «сильной» струи) имеем

32 ^pv ²

3(A - 1) ’ где A — 1 << 1. Если ввести параметр о = R°^°, то коэффициент интегрирования будет равен

32^pv² _     32v²        1      _ RUo

A — 1 +------ — 1 +       — 1 +    , v —----.

3Io          3 R2Uo2        6о2 ’         4о

A (A — cos Ө*)² (1 — A cos Ө*) sin² Ө*

Из выражения (11) находим 3 = —4 eoRq, где е =

В таком случае можно считать Ө << 1 и можно пользоваться оценкой cos Ө

1 — Ө2/2.

Если перейти к переменным ( р, X), где

^R р '- А,

(X — продольное расстояние от источника струи, R — радиус от оси струи), то первые два приближение для продольной скорости потока, приблизительно будут равны

-

^EoRo ^{(1 — 3}р²⁾ 1

X (1 + р2)    .

U « ^Ғ I ^Ғо -3 Q^R°^Uo [1

^U  ~ X ⁺ X ² =³ X (1+ р²)² I¹

Данное выражение совпадает с выражением для продольной скорости турбулентной струи, которое, таким образом, является приближением полученных выше выражений для «сильной» струи при условии постоянства, коэффициента, турбулентной вязкости. При этом возникают две эмпирических константы о и Ө*.

Для апробации полученных формул проведем сравнение с классическими опытными данными для осевой скорости. Из полученных выражений при A — 1 << 1 и Ө = 0 получим довольно простую формулу:

U _Н = Щ [1 — 2 eo^R + (2Eo^RД X   XX

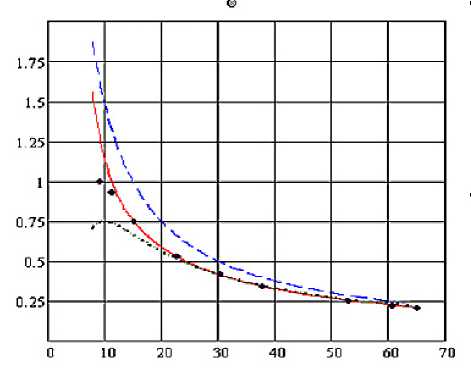
Рис. 1

На рис. 1 дано сравнение результатов расчета, по этой формуле (сплошная линия) с опытными данными [3] (показаны точками). Здесь же показаны (пунктир) первое и второе (штрихпунктир) приближения. По оси абсцисс указано безразмерное расстояние от среза, форсунки, отнесенное к ее радиусу, а по оси ординат - безразмерная скорость струи, отнесенная к скорости на выходе из трубки. Совпадение с опытными данными хорошее, если положить Ө* = 0.5 рад пи = 5.

Рассмотрим выражение (7). Первое приближение

____Ко____ г (А - cos Ө)28с для случая турбулентной («сильной») струи принимает вид

_____Ко_____

X (А - cos Ө)^28с.

Для продольной скорости в первом приближении имеем о     А2 - 1

^U1 ~ ² "х (А - cos Ө)².

Из последних двух выражений получим и аналогично,

Si max

Um UL)

Sc

Т1

т max

=(^ Г

Эти соотношения получены в [4].

Радиальное распределение концентрации вещества, отнесенной к S_max = ——.— ⁰ „ в X(А - 1)^2Ь<-

X функции безразмерного расстояния от оси струи в сечении — = 15 иллюстрирует рис. 2. Ко

По оси абсцисс указан безразмерный радиус, а по оси ординат S/Smax (штрихпунктирная линия — первое приближение, сплошная — второе).

Видно, что при учете второго приближения на. небольших расстояниях распределение концентрации приобретает вид седла, и количественно дает довольно существенную поправку. Заметна поправка и для азимутальной скорости при X/Ко = 20 (см. рис. 3). Здесь по

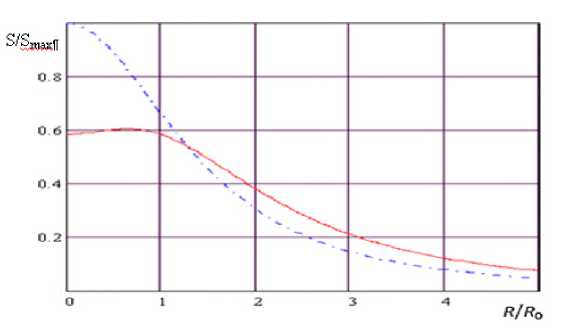
Рис. 2

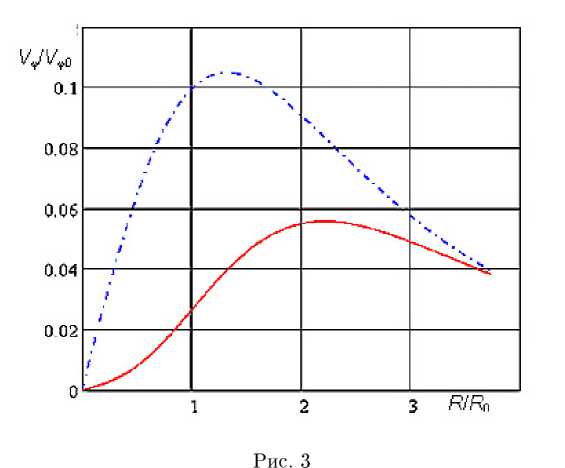
оси ординат дана безразмерная азимутальная скорость, отнесенная к максимальной азимутальной скорости на. выходе из трубки. Штрихпунктирная линия — профиль азимутальной скорости в первом приближении, сплошная — с учетом второго приближения. Видно, что положение максимума, для азимутальной скорости заметно смещается вправо. Отметим, что при построении данного графика, использованы эмпирические параметры для свобод-2^0

нои струи. Данный подход можно применить, если степень закрутки много меньше IoR-0

единицы, где Lo — плотность потока момента импульса.

Работа, выполнена, при поддержке РФФИ, гранты 09-08-00424, 10-08-00820 и в рамках программы «Развитие научного потенциала, высшей школы», проект № 10.11.