Аспекты математического моделирования процесса оперативной обработки информации в АИС морского торгового порта - ключевого звена экономики

Территориальный фактор для морских торговых портов (МТП) является одним из ключевых факторов, определяющих и обеспечивающих их конкурентоспособность. Создание и развитие современных автоматизированных систем управления (АСУ) МТП, направленных на формирование единого интеграционного транспортно-коммуникационного и экономического пространства, становится сегодня одной из приоритетных задач [1, 2, 3]. Так как значительно увеличиваются объемы мировых и российских грузопотоков, как экспортных, так и импортных, возникает необходимость получения оперативной, точной, защищенной информации обо всех объектах транспортного процесса. Например, по порту Новороссийск можно отметить, по оценкам аналитиков, рост на протяжении последних 10 лет, в связи с вышеуказанным фактом, только первичного информационного потока [4] из года в год в среднем около 25 %. Морские торговые порты, являющиеся сложными технико-экономическими и информационно-коммуникационными системами одновременно, можно детерминировать с позиций геоинформационной системы. Известно, что геосистема объединяет объекты и регионы пространства, ориентируясь на принцип содержательно- системной целостности на базе единой территориальной принадлежности. При этом модель геосистемы наряду с входящими в нее геообъектами характеризует взаимосвязи между ними, а также пространственно выражает территориальный носитель собственного системного качества. Модели геообъектов и геоситем – структурная основа для формирования функциональных тематических элементов системы геокибернетического моделирования. Весь информационно-коммуникационный процесс на морском транспорте – сложная система с множеством входных и выходных параметров, требующих четкой увязки, контроля, а самое главное, рационального моделирования и реализации модели на практике, что сегодня является особо актуальной и серьезной задачей.

Таким образом, вопросы моделирования информационного процесса в АСУ на морском транспорте (в МТП) с учетом территориального контекста требуют дополнительного изучения. Тем более это касается математического моделирования процесса оперативной обработки информации в морском порту в указанном аспекте, где есть целое поле с множеством неизвестных для исследования.

Итак, обстановка – центральная категория в системе геоинформационной поддержки управления практически каждой сложной технико-экономической системы (рис. 1). На ее базе выполняются все остальные этапы геоинформационного управления – анализ геоситуации, выработка вариантов решения, планирование, реализация решения. При моделировании обстановки с установленной степенью детализации формализуются три базовых аспекта:

• 1)    данные о территориальном объекте и своих подсистемах поддержки и обеспечения;

• 2)    информация о «негативных» (в том числе – форс-мажорных) факторах в районе;

• 3)    параметры и характеристики района взаимодействий объектов сложной системы.

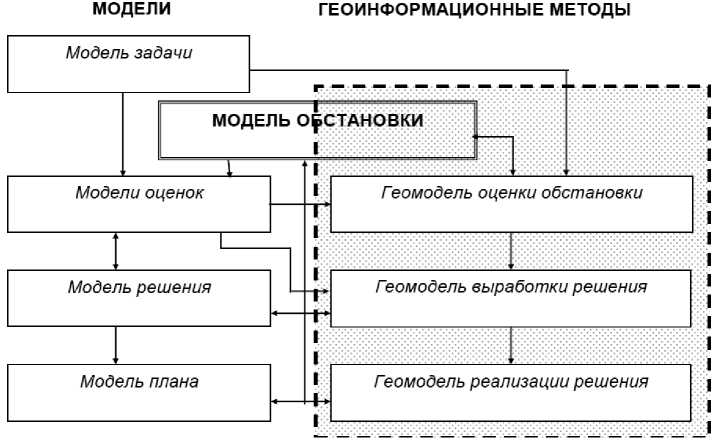
Рис. 1. Концептуальная система процесса геокибернетического моделирования

Она определяет содержание геомодели территориальной обстановки в АСУ МТП, что может быть представлено в следующем виде:

MSit i Maint = { CPFD, EnemD, CADD }, где CPFD – «свои силы»;

EnemD – «противник»;

CADD – район действий функционального территориального объекта (ТО, т. е. – торгового судна, единицы обеспеспечивающего флота, плавсредства, пререгрузочного объекта и т. д.). На рис. 2 показаны объекты ГС морского торгового порта.

Так как отображение обстановки должно в наибольшей степени соответствовать реальной геоситуации, объекты обстановки представляются в геоинформационном пространстве [5, 6, 7]:

Gob sit е GIS .

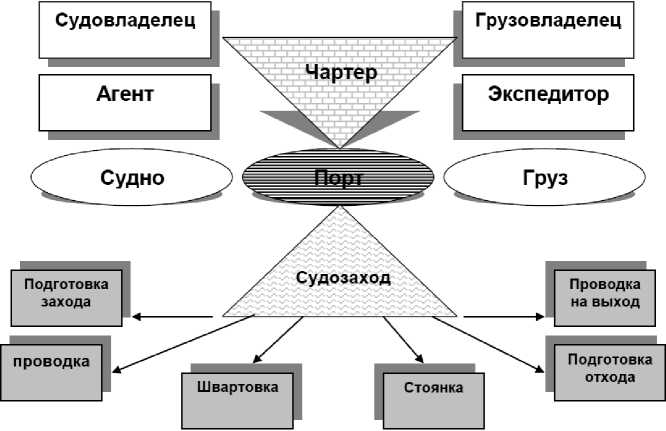
Рис. 2. Система взаимодействия объектов, участвующих в обработке грузопотока в морском торговом порту

Элементы обстановки представляются базовыми структурами геопространства (ГП) GSt (геообъекты, георегионы, геосистемы) и сопровождаются описанием их многомерного пространства признаков ( Descr) :

{ CPFD, EnemD, CADD } с <  GStr, Descr >.

Состав модели обстановки определяют модели геоданных:

MSit। cont = (Mp, Mo ), где Mp - цифровая модель поверхности района;

M o - цифровая модель объектов обстановки.

Модель поверхности территориально-морского района включает модели точек и контуров:

^M p = ^{ (^m t ) k - ^(m k ) k - P pt - P pk ^} где   ( m_t )_k - цифровая модель точки поверхности;

(m k ) k - цифровая модель контура поверхности;

P pt , P pk — предикаты (идентификаторы, правила, обозначения, ключевые параметры в реляционных таблицах пространственной базы данных) распределения точек и контуров на поверхности района.

Модель точки поверхности имеет следующий вид:

(mA = <  ^(x,y), Z ^(h) >  ’ где (x,y) - прямоугольные (плоские) координаты точки;

h - параметр (содержательный атрибут) точки;

Z (h) - символьная конструкция, описывающая значение отметки параметра (h):

Z ^(h) = 0, ⁽ x , y ) с ^{ ( m_t ) _к , P pk }, где   ^{{ (} m k ) k . P pk ^{} -} контур.

Множество точек ( M t ) k поверхности района ( m t ) _k имеет вид:

(M_t) k = { (m_t) k , P_pt }.

Модель контура (m^ )_k формируется на основе модели точки и включает:

(mt) к = < (У = fi(x)\x G [xn,xk])l ,(У = fj(x)\x G [xn,xk]) 2 ,-■• ...>(У = fr(x)\x G [xn,xk])X >, где y = f(x) - аппроксимирующие функции.

В таблице приведены выражения для модели контура в зависимости от формы представления геоданных объектов ГС - МТП.

Таблица – Формализация модели контура

Модель контура
Векторная:	Растровая:
M C = т Г Рк = U{ m h } k tk                  t   i j g N t,	m k = ( Mft , P t i , P t 2 ,..., P tq )
m k P „, = U« m h • m h »j j G N rk	Pti = <	1,   mt G M tk 0, emt e Mtki , i = 1, 2, ..., q
Nvk = {1, 2, ..., nvk } - вектора контура; mtk и mvk - модели начальной и конечной точек; Рк , P-к - системные параметры контура.	q - число контуров; Mtk - модели точек контуров; P , системные предикаты - принадлежности точек контуру.

Цифровая модель поверхности исследуемого района ( M p ) представляет набор контуров и точек района, а именно:

M p = ({Q h_V , O h 2 -■■■,Q hm }-(M t ) k ) , где O hi - кортежи, описывающие отдельные контуры (горизонтали, изобаты).

Ohi =< Z (hgi ),(У = fi (x)l x G [xn,xk])1 ,(У = fj (x)| x G [xn,xk]) 2 >■■■■■■.(У = fr(x)\x G [xn,xk])n > ,

где  Z(hgi) - символьная конструкция, соответствующая значению высоты hgt - контура (горизонтали);

• У = f (x) - функции и области задания функций, описывающих упорядоченные множества отрезков или дуг цифровых моделей контуров;

• ( M_t )_k - множество точек.

Модель объектов обстановки ( M_o ) предствляется как цифровое описание формы и содержательных признаков объекта, а также отношений на множестве объектов перевозочного процесса в МТП:

Mo = (M Fob ,{Ob}, Rob )• где MFob - модель формы объекта;

{ Ob } - множество содержательных признаков (описаний) объектов обстановки - перегрузочно-перевозочного процесса;

R_ob - модель отношений между исследуемыми объектами.

Модель формы объекта ( M_FOb ) подобно цифровой модели поверхности района описывает положение, контур или поверхность объекта.

Содержание объекта передается через групповые и индивидуальные характеристики его класса, вида и т. д. Данный процесс можно представить в следующей форме:

n    ^l i ^m j

{ Ob }- UUU ^Ob i,j,k •

• i = 1 j = 1 k = 1 где n - число классов объектов;

l - число родов i -го класса;

m j - число видов j -го рода.

Класс - множество объектов, имеющих общий существенный признак и отличающихся от всех других объектов других множеств по различному признаку. При этом общий признак для объектов одного класса выступает одновременно как различительный по отношению к объектам другого класса.

Род - подмножество объектов класса, все объекты которого имеют общий признак, существенный для этого подмножества, и отличаются от объектов других подмножеств класса по различительному признаку.

Вид - подмножество объектов рода, имеющих общий константный признак, существенный для решения конкретного вида задач.

Каждый объект обстановки ( Ob) в отдельности (конкретный географический объект, единичный элемент обстановки, его содержание) представляется в следуещей форме:

a d i

Ob - UU Pj • i=1 j=1

где Р - конкретное дискретное значение признака (атрибута) объекта;

а - общее число признаков в содержании объекта;

d_t - число дискретных значений в пределах каждого признака.

Модель признаков ( Р^ ) в этом случае представляется как:

l

Pj-< U рС > • i=1

где Р^С - содержательный признак объекта, Р С е Sⁿ ;

Sⁿ - многомерное пространство признаков.

Модель отношений между объектами ( R_ob ) отображает отношения объектов в

Sn -многомерном пространстве признаков объектов и в Rm -физическом пространстве: Rob = №№}) , где  rc - функция, отображающая содержательные отношения между объектами;

г _т - функция, отображающая пространственные отношения между объектами. Базовая их схема представлена на рис. 3.

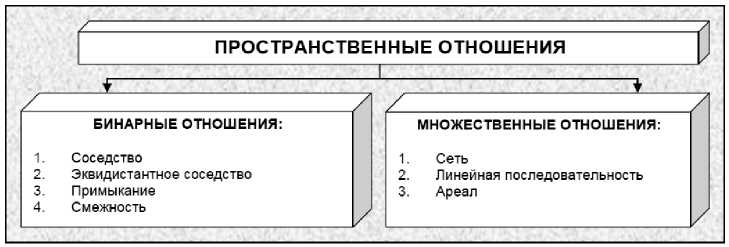
Рис. 3. Пространственные отношения между системными объектами транспортного процесса

Содержательные отношения определяются с помощью методов теории информации, множеств, классификаций и районирования, корреляционного, дисперсионного, факторного, системного и других видов анализа.

Пространственные отношения определяются взаимоотношением контуров или поверхностей объектов транспортного процесса:

Г = f( rt, rcэ, rcГ ) -c    cc c t где  rc - отношения, отображающие место объекта в содержательно-таксономическом ряду;

э rc - отношения между элементами составного объекта; Г r - групповые отношения (группировки).

r _т = f (о, с, <, ^, и, p v 0 = {0, 1}), где о - пересечение;

с - вложение;

• < - упорядочение;

^ - ориентирование;

и - наложение;

p v 0 = 0 - примыкание;

как дизъюнкция двух высказываний.

p v 0 = 1 - соседство,

Структура модели исследуемой обстановки представляет иерархическую систему цифровых моделей природных, социальных и экономических компонентов. Поэтому выражение цифровой модели обстановки ( т ^ ) на i -м иерархическом уровне обобщения принимает вид:

mi= {(Mi-1 Mi-1 ⊂Mi),(Pi-1

e         e      e         e      sc i-1        i sc        sc ,

где M_e – модели элементов обстановки;

P – системные параметры модели (отношения);

i – иерархический уровень модели (обобщения).

Данное выражение – совокупность некоторых множеств с заданными в нем бинарными отношениями; поэтому может рассматриваться как граф. Таким образом, модель обстановки представляется в виде ориентированного графа – дерева целей, где корень – модель обстановки, а вершины – цифровые модели элементов и системные параметры соответствующих уровней обобщения.

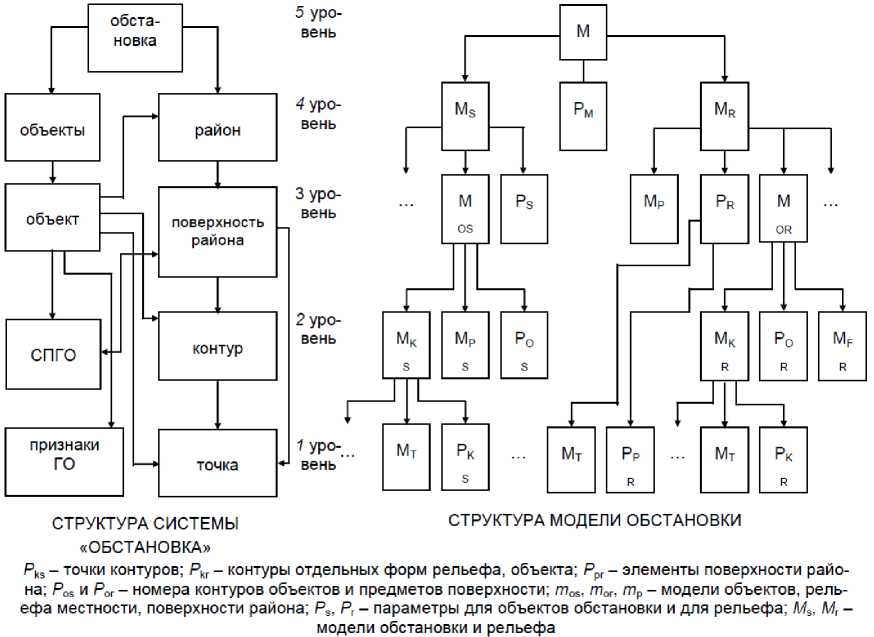
Рис. 4. Структура обстановки

Структура обстановки в сочетании с принимаемой при этом структурой системы «обстановка» включает следующие компоненты и уровни, что показано на рис. 4.

Первый уровень иерархии – элементарные неделимые информационные части моделей сложного пространственного объекта и пространственной поверхности – модели точек ( m_t ) и контуров ( m_k ).

Структурная целостность модели на указанном уровне задается совокупностью системных параметров, указывающих на геометрическую структуру контуров объектов района ( P ks ), контуров отдельных форм рельефа ( P kr ) или поверхности ( P pr ). Эти системные параметры – символьные коды, обозначающие характер связей точек в контуре (последовательность соединения, форму связи, геометрический вид, точность идентификации)

или характер расположения точек на ЗП (в характерных местах, по регулярной сетке, по профилям, по нерегулярной сетке и т. д.).

Второй уровень модели – это совокупность цифровых моделей контуров ( m ) и отдельных форм рельефа ( m_fr ), цифровых моделей контуров ( m _ks ) и поверхностей ( m ) самих объектов, а также системных параметров, определяющих соответствие контуров объектам ( P os ) и формам рельефа ( P or ). В качестве системных параметров P os и P or принимаются номера контуров объектов и предметов поверхности в соответствии с используемой системой идентификации УЗ или картографических элементов (кодификаторы, классификаторы).

Третий уровень модели включает цифровые модели объектов ( m os ) и рельефа местности ( m or ), модели поверхности района ( m p ) и объединяющие их параметры P s (для объектов обстановки) и P r (для рельефа). В качестве этих параметров выступают символьные коды, идентифицирующие объекты обстановки в соответствии с принятой системой обозначений (например, порядковые номера или координаты центра тяжести контуров).

Четвертый уровень иерархии составляют цифровые модели обстановки ( M s ) и рельефа ( M r ). Объединение их в соответствии с системными параметрами P m (единая система координат, одинаковая степень генерализации, временной диапазон и территориальный охват и др.) образует последний пятый уровень – саму модель обстановки.

Таким образом, модель обстановки – инвариант остальным моделям информационного обмена при осуществлении транспортного процесса, так как по своему составу и структуре может быть преобразована в другие формальные представления категорий управления на экономическом, социальном, финансовом и других уровнях. Особенно это касается процесса моделирования автоматизированного документооборота и в целом автоматизированной системы управления на морском транспорте.

Ссылки:

• 1.    Панамарева О.Н. Информационные технологии      1.

• 2.    Иванова С.Е., Панамарева О.Н. Повышение     2.

• 3.  Попов В.В. Развитие и безопасность южных3.

• 4.   Панамарева О.Н. Указ. соч.4.

• 5.   Байсеркеев О.Н., Бургоменко В.Н. Региональ-5.

• 6.    Биденко С.И., Самотонин Д.Н., Яшин А.И.6.

• 7.    Дьяконов К.Н., Касимов Н.С., Тикунов В.С.7.

в управлении морскими портами // Материалы IV Международной   научно-методической конференции   «Современный   российский менеджмент: состояние, проблемы, развитие» : сб. статей. Пенза, 2005.

эффективности работы морского порта путем использования информационных технологий // Известия высших учебных заведений. СевероКавказский регион. Проблемы водного транспорта. Спецвыпуск. Ч. II. Технические науки.

Ростов н/Д, 2006.

портов России : учеб. пособие. М., 2003.

ная предметно-пространственная среда. Алматы, 1993.

Геоинформационные модели и методы поддержки управления. СПб., 2003.

Современные методы географических исследований. М., 1996.