Assessment of Effective Risk in Software Projects based on Wallace’s Classification Using Fuzzy Logic

Published Online October 2013 in MECS

Software development projects face a number of software risks. The most important factors that may cause failure of project are related to poor performance, team pressure, low quality and high cost [1]. So software project risk management plays an important role in completing software projects successfully. It consists of the following four phases: identification, assessment, plan and control. Risk assessment is the base of software project risk management. According to [2] definition, risk exposure is expressed as the relationship RE=P(uo)*L(uo), where RE is the risk exposure, P(uo) is the probability of an unsatisfactory outcome and L(uo) is the loss to the parties affected if the outcome is unsatisfied[3].

The major problem associated with the estimation of risks is that the input data are imprecise by nature and it is difficult to represent them with crisp numbers. Usually the risk analyst prefers to estimate in linguistic terms such as high or low rather than in exact probabilistic terminology. To this end, the application of Fuzzy Set Theory (FST) to risk analysis seems appropriate; as such analysis can handle subjectivity as well as inexact and vague information [1].

The solution that is suggested here to overcome previously mentioned problems is to use fuzzy logic linguistic variables for the complexity metrics and model. Fuzzy logic is a mathematical tool for dealing with uncertainties and also it provides a technique to deal with imprecision and information granularity. Fuzzy logic is seen as a means of approximate reasoning. The fuzzy logic has been successfully applied in many segments such as engineering, psychology, artificial intelligence, medicine and sociology. In this paper we propose a fuzzy logic approach for risk estimation in software projects. We use five factors that are important in risk management. Those factors are Team, Planning, Complexity, Requirements and User.

Our fuzzy model has five input and we use 3 linguistic variables for each input. This membership functions are Low, Medium and High. Fuzzification module maps the non-fuzzy values in fuzzy space and defuzzification module convert the fuzzy numbers into crisp space. In our framework, after fuzzificaition of each input, the Mamdani inference system that includes a rule base can evaluate the risk of software project. This is a fuzzy number, so it should convert to a crisp number by a defuzzificaion algorithm. Number of rules in this rule base that use in this system is 243 and “And Method “ is min also “Or Method” is max, this mean that and operator between two numbers select minimum of numbers and or operator between two number select maximum of this numbers. Fuzzy inference is the actual process of mapping from a given input to an output using fuzzy logic. The process involves all the pieces: membership functions, fuzzy logic operators, and if-then rules. Results of experiments shows that our framework is more efficient than other frameworks and approaches for risk assessment in software projects.

The rest of this paper is organized as follows: Section 2 describes the related works. Section 3 describes the concepts and definitions . Section 4 explains the Wallace’s Work. Section 5 describes proposed approach and finally section 6 concludes the paper with some discussion.

• II.    RELATED WORK

  This section presents works that related to risk and risk management. Boehm [2] proposed a software risk management framework. He identified a list of the top-ten software risks based on his experience at TRW. There were some problems in his survey. The list of top-ten software risks lacked a theoretical foundation. Secondly, these risks are set according to software development environment in 1991 but scale and diversity of software have increased and thus, the list has become inadequate.

Barki et al. [4] conducted a survey in Quebec. They identified a list which included 23 software risks. They classified them into five groups. The list provided a comprehensible instrument but Wallace et al.[13] explained that the assessment scale of each risk was complex.

TABLE 1: summary of related studies on software risks

	Boehm	Barki et al.	Wallace et al.
Project Type	General	General	General
Scope	TRW	Quebec	Across Countries
Participant	Project Manager	Project Leader and User representative	PMI members
Participant numbers	Unknown	120	507
Research Method	Unknown	CFA	SEM
Dimensions	0	5	6
Risks	10	23	27

In our study, five of six risk dimensions of Wallace’s work were adopted. Firstly, her work was conducted in 2004, and thus it was relatively up-to-date and reflected the consensus of 507 PMI members from various countries. Secondly, SEM was used in her work to examine and prove the composite reliability, convergent validity and adequacy of the proposed framework of software risks. Therefore, the six risk dimensions and their associated software risks, as shown in table 2, were considered appropriate for our study.

This table has two columns, factors and sub factors. Factors are: user, requirement, project complexity, planning and control, team and organizational environment. For example sub factors of planning and control are: lack of an effective project management methodology, project progress not monitored closely enough, inadequate estimation of required resources, poor project planning, project milestones not clearly defined, inexperienced project manager and ineffective communication. Also sub factors of user are: Users resistant to change, Conflict between users, Users with negative attitudes toward the project, Users not committed to the project and Lack of cooperation from users.

TABLE 2: Software risks adopted in this study

Risk factor	Sub factors of risk
User	•     Users resistant to change •     Conflict between users •     Users with negative attitudes toward the project •     Users not committed to the project •    Lack of cooperation from users
Requirement	•    Continually changing system requirements •     System requirements not adequately identified •     Unclear system requirements •     Incorrect system requirements
Project complexity	•    Project involved the use of new technology •     High level of technical complexity •     Immature technology •     Project involves the use of technology that has not been used in prior projects
Planning and control	•    Lack of an effective project management methodology •     Project progress not monitored closely enough •     Inadequate estimation of required resources •     Poor project planning •     Project milestones not clearly defined •     Inexperienced project manager •     Ineffective communication
Team	•    Inexperienced team members •    Inadequately trained development team members •    Team members lack specialized skills required by the project
Organizational environment	•     Change in organizational management during the project •     Corporate politics with negative effect on the project •     Unstable organizational environment •     Organization undergoing restructuring during the project

• III.    CONCEPTS AND DEFINITIONS

• 3.1    Risk

• 3.2    Risk Management

In this section we have review on some concepts and definition.

Risk arises when organizations pursue opportunities in the face of uncertainty, constrained by capability and cost. The most common definition of risk in software projects is in terms of exposure to specific factors that present a threat to achieving the expected outcomes of a project [7]. A software risk (an uncertain event or condition with negative consequences on a software project) can increase the failure rate of a project if it is ignored [8]. Thus, the main purpose of software risk management is to identify managerial and technical problems before they occur so that actions can be taken to eliminate or mitigate their impact [6].

Currently, measuring the grade of risk mainly depends on the value of risk exposure. According to Boehm’s definition, risk exposure is expressed as the relationship RE=P(uo)*L(uo),where RE is the risk exposure, P(uo) is the probability of an unsatisfactory outcome and L(uo) is the loss to the parties affected if the outcome is Unsatisfied[3].

Risk in software projects is usually defined as the probability-weighted impact of an event on a project. In classical decision theory, risk was viewed as reflecting variation in the probability distribution of possible outcomes, negative or positive, associated with a particular decision [7].

There are two classes of software project risk: generic risks common to all projects, and project-specific risks. Some of these risks are easy to identify and manage. Others are less obvious or it is more difficult to predict their likelihood and/or impact. This is complicated by multiple project dimensions including size, structure, complexity, composition, context, novelty, long planning and execution horizons, and volatile change. Therefore, risk management in software projects is important to: help avoid disasters; avoid rework; focus and balance effort; and stimulate win–win situations [7].

As foreshadowed above, software project risk management is usually defined as a set of principles and practices aimed at identifying, analyzing and handling risk factors to improve the chances of achieving a successful project outcome and/or avoid project failure. Any variation in approach is usually in the ‘principles and practices’ employed within this conceptual understanding of risk management.

Most commonly, one or more of four inter-related approaches to risk management are found in the literature and practice. These are checklists, analytical frameworks, process models, and risk response strategies [7].

Risk management can lead to a range of project and organizational benefits including:

• •     Identification of favourable alternative courses

of action;

• •    Increased confidence in achieving project

objectives;

• •    improved chances of success;

• •    Reduced surprises;

• •    More precise estimates (through reduced uncertainty);

• •    Reduced duplication of effort (through team awareness of risk control actions) [7].

• IV.    WALLACE’S WORK

  In our study, the six risk dimensions of Wallace’s work were adopted. Firstly, her work was conducted in 2004, and thus it was relatively up-to-date and reflected the consensus of 507 PMI members from various

And also:

Uto f х — 1

m — 1,

1 , I и — х и — m^⁰

I 0

1 < х < m;

х = m;

m < х <  и , others;

V. PROPOSED APPROACH

Before presenting the proposed method, let’s review some basic definitions related to fuzzy logic.

Definition 1 :

If our universe is X, then fuzzy set A would be as follows:

For defuzzification of risk final amount we can use center of gravity technique. This technique developed by Sugeno in 1985. This technique is most commonly used method and is very accurate. Center of gravity technique is described as follows [11-13].

A = {< х, j_A (х) >• х е X}

/ p.t (х) х йх х =“г---д—

J jU t х ах

Membership function ц _а (x) when x is a member and ц_А : X ^ [0,1] : specifies degree of membership x to set A [8, 9]

Definition 2 :

A ={< X, J a (х), V_A (х ) >|хеХ} (2)

Definition 3 :

A triangular fuzzy number can be sorted with a trio (1, m, u) that 1 and u are upper and lower limits, m is middle and x is an element between 1 and 0 as shown in Figure 1.

x * Defuzzy output, x * total membership function and x is output variable.

In this paper we use five factors that described in Wallace’s work. These factors are user, requirements, complexity, planning and Team. Figure 1 shows the model. In this model, the final output of the projects software risks are due to five factors.

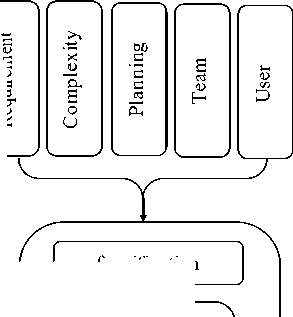
К

E

'5

fuzzification

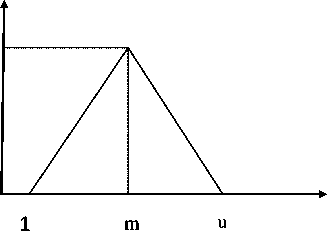
Figure 1: Triangular fuzzy number

Fu zzy Inference System

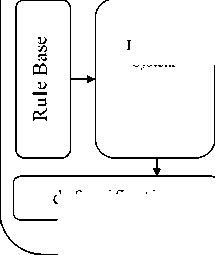
defuzzification

Risk

Figure 2: Software risk assessment model

TABLE 3: Implementation of fuzzy inference system

System	Name='RiskEvaluation', Type='mamdani', Version=2.0, NumInputs=5, NumOutputs=1, NumRules=243, AndMethod='min', OrMethod='max', ImpMethod='min', AggMethod='max', DefuzzMethod='centroid'
Input1	Name='User', Range=[0 1], NumMFs=3, MF1='Low':'trimf',[0 0.16 0.33], MF2='medium':'trimf',[0.30 0.45 0.62], MF3='high':'trimf',[0.57 0.85 1]
Input2	Name=’ Requirement ', Range=[0 1], NumMFs=3, MF1='low':'trimf',[0 0.16 0.34], MF2='medium':'trimf',[0.30 0.45 0.62], MF3='high':'trimf',[0.56 0.85 1]
Input3	Name='Complexity', Range=[0 1], NumMFs=3, MF1='low':'trimf',[0 0.16 0.35], MF2='medium':'trimf',[0.30 0.45 0.62], MF3='high':'trimf',[0.56 0.80 1]
Input4	Name='Planning', Range=[0 1], NumMFs=3, MF1='low':'trimf',[0 0.16 0.34], MF2='medium':'trimf',[0.30 0.40 0.65], MF3='high':'trimf',[0.60 0.85 1.0]
Input5	Name='Team', Range=[0 1], NumMFs=3, MF1='low':'trimf',[0 0.16 0.33], MF2='medium':'trimf',[0.30 0.45 0.62], MF3='high':'trimf',[0.58 0.85 1.0]
Output	Name=' RiskEvaluation ', Range=[0 1], NumMFs=5, MF1='Very_Low':'trimf',[0.0 0.12 0.23], MF2='Low':'trimf',[0.20 0.32 0.42], MF3='Medium':'trimf',[0.40 .51 0.62], MF4='High':'trimf',[0.60 0.75 0.82], MF5='Very_High':'trimf',[0.80 .91 1.0]

Output categorize in five category that are very low risk project ( Very Low ), Low-risk project ( Low ), Medium-risk project ( Medium ), High-risk project ( High ) and very high risk Project ( Very High ). We use 3 linguistic variables for each input. Number of rules generated is equal to 243. We can see some of generated rules below. According to input data for each input, one of the rules is activated.

Number of generated rules is equal to 243. Corresponding Membership functions cut and after defuzzification, final output calculates.

• 5.1    Rules description

We have five input and we use 3 linguistic variables for each input. Therefore numbers of rules are 243. The following block of code shows some rules:

Rule 1: If (User is Low) and (Requirement is Low) and (Complexity is Low) and (Planning is

Low) and (team is Low) then (Risk is Very Low) Rule 2: If (User is Low) and (Requirement is Low) and (Complexity is Low) and (Planning is Low) and (team is Medium) then (Risk is Low)

Rule3: If (User is Low) and (Requirement is Low) and (Complexity is Low) and (Planning is Low) and (team is High) then (Risk is Low)

Rule4: If (User is Low) and (Requirement is Low) and (Complexity is Low) and (Planning is Medium) and (team is High) then (Risk is Low)

Rule5: If (User is Low) and (Requirement is Low) and (Complexity is Low) and (Planning is High) and (team is High) then (Risk is Low)

Rule6: If (User is Low) and (Requirement is Low) and (Complexity is Medium) and (Planning is Low) and (team is High) then (Risk is Low)

Rule7: If (User is Low) and (Requirement is Low) and (Complexity is High) and (Planning is Low) and (team is High) then (Risk is Low)

Rule8: If (User is Low) and (Requirement is Medium) and (Complexity is Low) and (Planning is Low) and (team is High) then (Risk is Low)

Rule9: If (User is Low) and (Requirement is High) and (Complexity is Low) and (Planning is Low) and (team is High) then (Risk is Low)

Rule241: If (User is High) and (Requirement is High) and (Complexity is High) and (Planning is High) and (Team is Low) then (Risk is High)

Rule242: If (User is High) and (Requirement is High) and (Complexity is High) and ( Planning is High) and (Team is Medium) then (Risk is Very High )

Rule243: If (User is High) and (Requirement is High) and (Complexity is High) and (Planning is High) and (Team is High) then (Risk is Very High)

Mamdani inference used to implement the fuzzy inference system. System information is presented in Table 3. According to table 3 this system has 5 inputs and 1 output. Inputs are: User Requirement, Project complexity, Planning and Team. Number of fuzzy rules that use in this system is 243 and “AndMethod “ is min also “OrMethod” is max, this mean that and operator between two numbers select minimum of numbers and or operator between two number select maximum of this numbers. Range of each inputs, output and fuzzy linguistic variable is shown in table 3. For example: input 2 has 3 membership function named: Low, Medium and High. Range of Low is 0.0 - 0.33, Medium is 0.30 – 0.62 and High is 0.57 – 1.0 and type of membership function is trimf. Also for output variable that is value of software project risk, there are five membership function that name and range of them are: VeryLow [0.0 0.12 0.23], Low [0.20 0.32 0.42], Medium [0.40 .51 0.62], High [0.60 0.75 0.82] and Very High [0.80 .91 1.0], type of those membership functions are trimf and name of this output variable is risk evaluation in Mamdani inference.

• 5.2    Membership Function Assignment

The following example illustrates how the membership grade is assigned to output. The inputs are fed to the fuzzification module and after fuzzification of given values we find that user=0.90 belongs to High membership function, requirement = 0.87 belongs to

High membership function, complexity=0.64 belongs to High membership function, planning=0.76 belongs to High membership function and team=0.18 belongs to Low membership function, so:

Rule# : if (user=0.90) and (requirement = 0.87) and (complexity=0.64) and (planning=0.76) and (team=0.18) then (?)

With these input values the following rule gets fired:

Rule241 : If (User is High) and (Requirement is High) and (Complexity is High) and (Planning is High) and (Team is Low) then (Risk is High)

The rule gives the output value as High which indicates the high risk for software project.

Another example of how the membership grade is assigned to output:

User =0.11 belongs to Low membership function, requirement = 0.18 belongs to Low membership function, complexity=0.31 belongs to Low membership function, planning=0.06 belongs to Low membership function and team=0.25 belongs to Low membership function, so:

Rule# : if (user=0.11) and (requirement = 0.18) and (complexity=0.31) and (planning=0.06) and (team=0.25) then (?)

With these input values the following rule gets fired.

Rule1 : If (User is Low) and (Requirement is Low) and (Complexity is Low) and (Planning is Low) and (Team is Low) then (Risk is VeryLow)

The rule gives the output value as VeryLow which indicates the VeryLow risk for software project.

• 5.3    Assessment

The proposed model was implemented for four projects. Details of these projects are described in table 4.

Table 4: System results for some projects

	Project 1	Project 2	Project 3	Project 4
Team	0.198	0.752	0.988	0.380
Planning	0.134	0.907	0.875	0.537
Complexity	0.089	0.085	0.798	0.434
Requirement	0.165	0.077	0.909	0.614
User	0.251	0.124	0.034	0.555
Risk Evaluation	0.182	0.798	0.819	0.592

For example in project p1, after fuzzification of inputs, user factor equals 0.251, requirement factor equal to 0.165, the complexity factor equals 0.089, the planning factor is equal to 0.134 and team factor is equal to 0.198. According to these characteristics, rule 1 gets fired and by defuzzification of fuzzy value with center of gravity method, output was equaled to 0.182. Another example of this table is p3, after fuzzification of inputs, user factor equals 0.034, requirement factor equal to 0.909, the complexity factor equals 0.798, the planning factor is equal to 0.875, and team factor is equal to 0.988.

After firing the rule and defuzzification of fuzzy value with center of gravity method, output was equaled to 0.819

• VI. CONCLUSION

In this paper we made short review of risk management, classification of it and factors that affecting it and presented an efficient method to measure software risk using fuzzy logic. This fuzzy system has 5 inputs and one output. Number of fuzzy rules in this system is 243 and each input has 3 membership functions. The presented system is based on 5 factors: Team, Planning, Complexity, Requirements and User. Those factors are very important for managers of software projects. Very important decisions in software projects are made on these factors. The presented system was tested on four projects and risk of the projects was calculated. Software project team can use this information to make appropriate decisions in order to deal with the project.

ACKNOWLEDGMENTS

This research was partially supported by the Agricultural Sciences and Natural Resources University of Gorgan and Mazandaran University of Sciences and Technology.