Астрономические источники первичной навигационной информации для автономного определения движения объектов

Астрономические источники ПНП, а также методы и ные на использовании этой информации, в значительной средства решения задачи навигации в космосе, основан- степени определяют успех выполнения всех задач, кото- рые ставятся перед космическими системами самого различного назначения. В настоящее время практически нет таких космических аппаратов и кораблей, в составе бортовых систем которых не были бы представлены устройства навигации и ориентации, основывающиеся на использовании информации, получаемой отастрономи-ческих источников.

Для целей навигации и ориентации в космическом пространстве могут использоваться все поля, возбуждаемые астрономическими объектами: электромагнитное (во всем возможном диапазоне длин волн отультрафио-лета до радиодиапазона), магнитное, гравитационное. При этом первичной навигационной информацией могут являться результаты измерений любых физических величин, обусловленных полями, характеристики которых зависят откоординати скорости КА. К числу таких величин можно отнести величину и градиенты полей, интенсивность излучения, углы положения астрономических ориентиров относительно некоторых направлений, удаленность отповерхности близких небесных тел, измеряемую дальномерами [1].

Измерение положения звезды относительно направления текущего радиус-вектора.

Пусть r – радиус-вектор, определяющий положение КА в некоторой системе координат OXYZ (риc. 1), a s0 – единичный вектор, направленный из начала координат в точку расположения неподвижной звезды. Обозначим буквой β угол между r и s0. Величина этого угла определяется простым выражением rs0xa0+yb0+zc0 β = arccos=, r    (x2+y2+z2)1/2

где x , y , z – составляющие радиус-вектора r в системе OXYZ , a ⁰, b ⁰, c ⁰– составляющие единичного вектора s ⁰ в системе OXYZ .

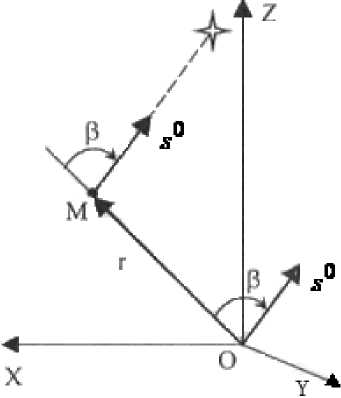
Рис. 1. Схема измерения зенитного расстояния

Зная положение звезды и измерив угол β , который называют зенитным расстоянием, можно лишь указать, что КА находится на конической поверхности с вершиной в точке О , образованной вращением луча вокруг вектора s ⁰ лучом под углом β . На одной из образующих этой поверхности лежит вектор r .

Измеряя зенитное расстояние второй звезды, построим вторую коническую поверхность. Две линии пересечения (в общем случае) полученных поверхностей по-зволяютопределить два направления возможного положения радиус-вектора r . С одним из этих направлений совпадаетистинное положение r .

Уравнения прямых, соответствующих двум направлениям r , определяются в результате совместного решения двух уравнений, отличающихся только коэффициентами a ⁰, b ⁰, c ⁰. Для нахождения положения КА необходимо измерить третье зенитное расстояние и построить третью коническую поверхность, однако выбор из двух направлений того, которое соответствует положению КА, обычно не представляет затруднений.

При r << ∞ для реализации этого состава измерений необходимо располагать бортовыми устройствами, воспроизводящими направление радиус-вектора r и осуществляющими пеленгацию звезд. При полетах вблизи небесных тел такими устройствами могут являться приборная вертикаль и автоматический секстант. При этом все измерительное устройство целесообразно осуществлять в виде единого блока, позволяющего избежать промежу- 0 точных вычислений по приведению составляющих r и s к единой системе отсчета.

Чувствительность измеряемого угла β к изменению координат x , y , z определяется производными, полученными дифференцированием уравнения (1):

∂β = ∂ x ⎜	⎛ x cos β ⎝ r	- a 0 ⎟⎠	r sin β ,
∂β = ∂ y ⎜	y cos β ⎝ r	- b 0 ⎞⎟⎠	r sin β ,
∂β = ∂ z ⎜	⎛ z cos β ⎝ r	0 ⎞ - c ⎟	r sin β ,	(2)

Связь между приращением ∂β угла β и малым отклонением ∂ r радиус-вектора r определяется формулой [1]

nδr ∂β =    ,

r

где n – единичный вектор, лежащий в плоскости измерений и перпендикулярный вектору r . Плоскость измерений образуется векторами s ⁰ и r , проходящими через начало координат.

Измерение видимого углового диаметра Земли. Если геометрический центр сферической Земли расположен в точке, определяемойрадиус-вектором rп (рис. 2), то ее видимый угловой диаметр d находится с помощью выражения d = 2γ =2arcsin п =

ρ

= 2arcsin      ₂^п_221/2 , (4)

⎡⎣(xп-x)+(yп-y)+(zп-z)⎤⎦ где Rп – радиус Земли; xп,yп,zп–его составляющие по осям X ,Y,Z; ρ =rп -r– радиус-вектор, определяющий взаимное положение центров КА и Земли; ρ –мо-дуль радиус-вектора.

Если начало системы координат OXYZ совмещено с геометрическим центром O Земли, то rп = 0 и выражение (4) принимаетвид d = 2 arcsin

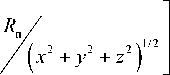
mδr δγ =-    tgγ ,

r

При измерениях видимого углового диаметра реаль-

ных планет вследствие сжатия и отклонения рельефа от правильной сферической поверхности появляются мето-

дические погрешности, детерминированный учет кото-

рых представляет практически неразрешимую задачу.

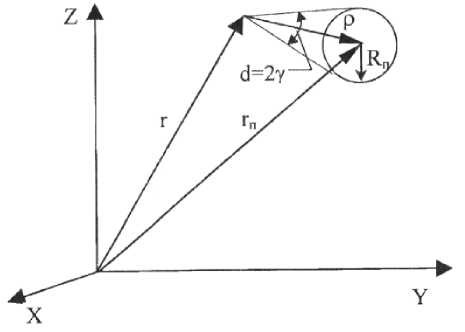
Рис. 2. Схема измерения видимого углового диаметра Земли

где m – единичный вектор, направленный из центра Земли в точку наблюдения (вдоль вектора r ).

Измерение положения звезды относительно линии видимого горизонта. Пусть начало системы координат OXYZ совмещено с центром сферической Земли O , имеющим радиус R _п (рис. 3). Обозначим: r – радиус-вектор положения КА; s ⁰ – единичный вектор направления на бесконечно удаленную звезду; β –уголмежду r и s ⁰ в точке наблюдения.

Тогда угол Ф между направлением на звезду и линией видимого горизонта определится выражением

Ф = π-β-γ , (8) где β – определяется равенством (1), а γ выглядитследую-щим образом:

R п

γ = arcsin = arcsin R r               ^⎢⎣

.

Однако при наличии некоторых усредненных характеристик распределения рельефа такой учет может быть произведен в статистическом плане. Так, например, в результате обработки данных об истинных фигурах Зем-лииЛуны могут быть получены статистические оценки погрешностей измерения видимых угловых радиусов δγ этих небесных тел, определяемых расстоянием до их центров δ r [1]. С вероятностью 90 % эти погрешности имеют следующие значения: погрешности от отклонений рельефа поверхности Земли относительно уровня сфероида (без учета рефракции)

0,95          0,95

δγ=            _1/2 ; δ r =      ;

(r2-Rп2)1/2          Rп погрешности от сжатия земного сфероида

п   ( x ² + y ² + z ² ) ^1/2

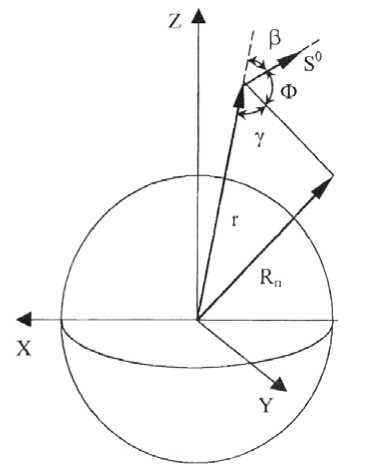
Рис. 3. Измерение положения звезды относительно видимого горизонта

δγ =

0, 243 R _э ² ε ²

r ²

1/2

; δr =

0,243 R _э ² ε ²

r

Следуетиметь в виду, что ошибки измерения угла γ вблизи Земли в реальных условиях будут значительно выше приведенных за счетразмытости самого горизонта светящейся атмосферой.

Производные, характеризующие чувствительность угла d к изменению координат, имеют вид x-xd

∂d∂x=-22 п tg, ρ2

∂d∂y=-2y-yп tgd , ρ2

∂d∂z=-2z-2zп tgd .(6)

ρ2

Если центр Земли совмещен с началом системы координат, то в формулах (6) необходимо учесть, что ρ = r , x _п = y _п = z _п = 0.В общем случае для сферической Земли радиусам R _п , связь между приращениями δ r вектора r и угла δγ = δ ( dI 2 ) определяется формулой

В большинстве случаев звезды Земли не являются сферическими, и для точных измерений необходимо было бы учитывать истинное значение R _п в точке горизонта под звездой. Однако такой учет ведет к значительному усложнению всех вычислений. Поэтому расчет по формуле (9) допустим только для измерений, производимых на значительных удалениях от планет с относительно небольшим сжатием. На очень малых удалениях от поверхности Земли некоторое повышение точности может быть достигнуто в результате учета радиуса Земли в точке пересечения радиус-вектора ^r с ее поверхностью. Так, например, если высота полета КА над поверхностью Земли составляет 150–180 км, то при совмещении оси Z с полюсом мира радиус Земли в горизонте может быть принятравным ее радиусу R _п в подспутниковой точке. Если при этом считать, что фигура Земли соответствует эллипсоиду вращения с экваториальным радиусом R _э и сжатием ε , то радиус подспутниковой точки имеет вид

R п = R э ( 1 -ε z ² r ² )

откуда

γ = arcsin

R э

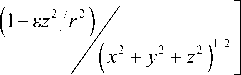
Связь между приращениями радиус-вектора r ииз-меряемого угла Ф можетбыть найдена дифференцированием уравнения (8).

∂Ф   ∂β ∂γ

В результате получим =-  -,

∂x∂

∂ Ф _=- ∂β _- ∂γ ∂ Ф _=- ∂β _- ∂γ где производные ∂ y ∂ y ∂ y , ∂ z ∂ z ∂ z ,

^∂β _, ^∂β _, ^∂β вычисляются по формулам (2).

∂x ,∂y,∂z

Производные γ вычисляются по формулам (6) с ∂q заменой ρ на r . Малые приращения угла Ф связаны с приращениями вектора r уравнениями

1 ∂ Ф = ( n r

- mtgy ) δ r ,

где n – единичный вектор, лежащий в плоскости, образуемой векторами r и s ⁰ , и перпендикулярный вектору r ; m – единичный вектор в точке наблюдения, направленный по вектору r . Таким образом, данный состав измерений по своим информативным свойствам эквивалентен одновременному измерению зенитного расстояния β звезды и углового диаметра d Земли. Методические ошибки, обусловленные сжатием и рельефом Земли, при измерениях угла Ф могутбыть учтены по тем же формулам, что и для измерений видимого углового диаметра d Земли.

Измерение угла между звездой и известным ориентиром на поверхности Земли. Совместим начало системы координат OXYZ с геометрическим центром Земли О (рис. 4). Пусть r – радиус-вектор положения КА; r _оп – радиус-вектор, определяющий положение ориентира на поверхности Земли; s ⁰ – единичный вектор, направленный на бесконечно удаленную звезду.

Тогда угол β между векторами s ⁰ и ρ = r - r _оп определится выражением

_{β= arccos} ( x - x ор ) a 0 + ( y - y ор ) b 0 + ( z - z ор ) ₁ c _/ 0 _{2 .(12)} ^⎡ _⎢⎣ ( x - x ор ) + ( y - y ор ) + ( z - z ор ) ^⎤ _⎥⎦

Производные, определяющие связь между малыми приращениями угла β и координат x , y , z ,имеютсле-дующий вид:

∂β I ∂ x =⎡_⎣ ( x - x _ор ) cos β- a ₀ ρ⎤_⎦ρ ² sin β ,

∂β /∂y=⎡⎣(y-yор)cosβ-b0ρ⎤⎦ρ2sinβ,

∂β /∂ x =⎡_⎣ ( z - z _ор ) cos β- c ₀ ρ⎤_⎦ρ ²sin β , (13) где ρ – радиус-вектор, направленный из точки наблюдения к точке на поверхности Земли. Связь между малыми приращениями ∂β и δ r определяется выражением

∂β = n ₁ δ r /ρ , (14) где n ₁ – единичный вектор, перпендикулярный вектору ρ и лежащий в плоскости, образуемой векторами s ⁰ и ρ .

Возможности использования для навигации некоторых физических полей. Помимо электромагнитного и гравитационного полей астрономические объекты име-ютдругие поля, которые принципиально могутявиться источниками ПНП. К их числу относятся магнитное и электростатическое поля, а также поле атмосферы. Однако к настоящему времени только магнитное поле Земли изучено в такой степени, что оно может быть практически использовано для навигации в космосе.

В первом приближении магнитное поле Земли может быть представлено в виде поля однородного намагниченного шара или поля центрального диполя. Начало вектора магнитного момента М этого поля совмещено с геометрическим центром эллипсоидальной Земли, и он наклонен под углом 11°30'к ее оси вращения. Вектор напряженности T этого поля (как поля диполя) описывается уравнением

T =

rM

M - 3 2 r r ²

r ³

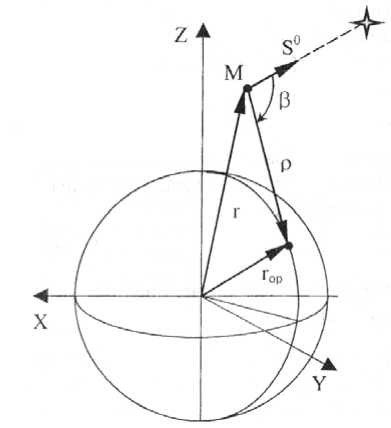
Рис. 4. Измерение положения звезды относительно ориентира на поверхности

где r – радиус-вектор точки наблюдения в геоцентрической системе координат.

Фактическое магнитное поле имеет более сложную структуру, причем меняющуюся во времени. Причинами отклонения реального поля Земли от дипольного и его изменения во времени являются мировые и региональные аномалии, изменение интенсивности и распределения токовых систем внутри тела Земли и токовых систем в атмосфере.

При среднем значении напряженности магнитного поля Земли γ ее поверхности, равном 3 - 10⁴ γ ( γ – гамма-единица, соответствующая 10⁵Э), вековыевариации магнитного момента от изменения внутренних токовых систем достигают 20 γ в год. При этом систематический дрейф момента к западу составляет 0°15'в год.

Атмосферные токовые системы в спокойное время создают магнитное поле интенсивности 20 γ …70 γ на расстоянии трех радиусов Земли ( r ≈ 20000км)и10 γ ...20 γ на ее поверхности. Это поле подвержено наиболее ин-

тенсивным и быстрым изменениям, обусловленным процессами в атмосфере и активностью Солнца. При этом могутнаблюдаться глобальные возмущения, охватывающие всю Землю, с изменениями интенсивности в несколько тысяч гамм при продолжительности в несколько суток; месячные возмущения с изменением интенсивности в сотни гамм при продолжительности в несколько часов; наконец, высокочастотные флюктуации интенсивности в несколько гамм и с периодом до нескольких минут. Статистические характеристики всех возмущений магнитного поля Земли в настоящее время достаточно хорошо изучены. Это позволяет создать математическую модель этого поля, относительно точно описывающую реальное поле.

Математическое ожидание T ₀ вектора напряженности как среднее по множеству многолетних измерений, описывается разложением его составляющих T_x , T_y , T_z в геоцентрической системе по шаровым функциям [1]:

• ^{∞ n} ⎡⎛ _R ⎞ ^{n + 2}                            ⎛ _r ⎞ ^{n - 1} ⎤ d ⎡ P_n^k ( cos θ ) ⎤

T =⎢ I^k cos k λ+ i^k sin k λ ^з + E^k cos k λ+ e^k sin k λ ⎥ ^{⎣ ⎦} , ^{x ∑} n = 1 ^∑ k = 0 ⎢_⎣^{( nn )⎜}⎝ r ^⎟⎠ ^{( nn )⎜}⎝ R з ^⎟⎠⎥_⎦ d θ ^,

∞ n ⎡ _kk ⎛ R ⎞ ^{n + 2} _kk ⎛ r ⎞ ^{n - 1} ⎤ d ⎡_⎣ P n ^k ( cos θ ) ⎤_⎦ T =⎢ I^k sin k λ- i^k cos k λ ^з + E^k sin k λ- e^k cos k λ⎥ , ^{y ∑} n = 1 ^∑ k = 0 ⎢_⎣^{( nn )⎜}⎝ r ^⎟⎠ ^{( nn )⎜}⎝ R з ^⎟⎠⎥_⎦ d θ ^,

Tx=∑∞ ∑n ⎢(Inkcoskλ+inksinkλ)(n+1)⎛⎜Rз⎞⎟+(Enkcoskλ+enksinkλ)n⎛⎜r ⎞⎟⎥d⎣Pn (cosθ)⎦, (16) n=1k=0⎢⎣                                   ⎝r⎠                                     ⎝Rз ⎠⎥⎦dθ где Rз – радиус сферической поверхности Земли; λ – географическая долгота; θ=90o -ϕ ( ϕ – географическая широта); Pnk (cos θ)– присоединенные полиномы Лежандра 1-го рода; kk k k– нормированные n,n,n,n коэффициенты, зависящие от внутренних и атмосферных источников магнитного поля Земли. В настоящее время эти коэффициенты определены с относительно высокой точностью.

Первая гармоника этого разложения ( n = 1 ) соответствует полю диполя. Точность знания входящих в уравнения (16) коэффициентов позволяет вычислять поля с учетом до 10-й гармоники ( n = 10). При этом расчетные значения составляющих Г₀ отличаются от фактически измеренных не более чем на 0,1...1,5 % при r ≤ R _з . С увеличением удаленности более 5 R _з ошибки быстро возрастают.

Помимо математического ожидания при расчете магнитного поля Земли необходимо учитывать случайные составляющие δ T , в большинстве своем носящие нестационарный характер как во времени, таки в пространстве. В настоящее время с помощью магнитометрической аппаратуры уже накоплена значительная информация о статистических характеристиках магнитного поля Земли на различных высотах от ее поверхности и о вариациях этих характеристик во времени. Это создает определенные предпосылки к тому, что в будущем при достаточном уточнении таких характеристик могут быть созданы условия для практической реализации навигационных систем искусственных спутников Земли, основанных на магнитометрических измерениях.

В основу построения таких навигационных систем могутбыть доложены две основные схемы: с измерением полного вектора напряженности T и измерением лишь его модуля.

В первом случае магнитометрический измерительный блок, состоящий из трех магнитометров с ортогонально расположенными осями чувствительности, дол- жен устанавливаться на площадке, стабилизированной в инерциальном пространстве или системе координат, связанной с Землей. Оси магнитометров ориентируются (с точностью до инструментальных и методических ошибок) по осям инерциальной или связанной с Землей системами координат. При этом каждый магнитометр измеряет составляющую вектора T по соответствующей оси. Если бы магнитное поле было детерминированным и описывалось уравнением (13), знание составляющих вектора позволило бы однозначно определять место его измерения, т. е. находить координаты КА. Однако уже из-за регулярных вариаций, учитываемых в уравнении (14), по одному измерению место измерения определяется неоднозначно, поскольку вектор T по величине и направлению может иметь одно ито же значение во многих точках. Случайные вариации приводят к тому, что количество точек становится весьма большим и даже может стремиться к бесконечности. Техническая реализация навигационной системы, базирующейся на измерениях полного вектора T, является весьма сложной проблемой из-за необходимости материализации стабилизированной платформы. Особенно трудно создать на подвижном объекте платформу, связанную с фиксированной относительно Земли системой координат.

Навигационные системы, базирующиеся на измерениях модуля вектора напряженности T , технически реализуются гораздо проще, так как они не требуют наличия стабилизированной платформы. Измерительный блок, состоящий, какив первом случае, из трех магнитометров с ортогонально расположенными осями, может быть установлен на корпусе объекта. В любой момент времени и при любой ориентации измерительного блока модуль вектора T рассчитывается по формуле 1/2

T = ( T x ² + T y ² + T z ² ) ,              (17)

где T_x , T_y , T_z –измеренныесоставляющиевектора Т по осям измерительного блока.

Однако определение места по измеренным значениям модуля вектора становится весьма сложной задачей, так как любому его значению соответствует поверхность весьма сложной конфигурации. Неоднозначность определения места как по измерениям полного вектора напряженности T , так и его модуля делает неизбежным вывод, что навигационные магнитометрические системы могут работать только в режиме уточнения места наблюдения. При этом предварительная оценка места должна быть достаточно точной, точность знания магнитного поля – весьма высокой, а навигационная задача должна решаться статистическими методами, по результатам обработки большого количества измерений.

Исходя из выше сказанного, использование астрономических источников первичной информации для автономного определения движения объектов является весьма актуальной для космической отрасли.

Библиографическая ссылка

Analyzed astronomical sources of primary navigation information for autonomous determination of the motion of objects.

А. В. Кацура, В. А. Лавренов, А. А. Рябин

ПРИМЕНЕНИЕ МЕТОДОВ НЕРАЗРУШАЮЩЕГО КОНТРОЛЯ ДЛЯ ВЫЯВЛЕНИЯ КОРРОЗИОННЫХ ПОРАЖЕНИЙ ЭЛЕМЕНТОВ КОНСТРУКЦИЙ ЛЕТАТЕЛЬНЫХ АППАРАТОВ

Использование этих методов на различных этапах эксплуатации обеспечивает достоверность оценки технического состояния летательных аппаратов (ЛА).

Применение методов неразрушающего контроля для исходного материала, заготовок, полуфабрикатов и готовых деталей на этапах производства авиационной техники способствует выпуску продукции высокого качества. Использование методов неразрушающего контроля на различных этапах эксплуатации при выполнении периодических и целевых технических осмотров обеспечивает предотвращение лётных происшествий, полную выработку назначенных и межремонтных ресурсов и их обоснованное увеличение при сохранении заложенного уровня надёжности, повышение достоверности оценки технического и коррозионного состояния высоконагруженных элементов конструкции.

Контроль технического состояния выполняется для получения информации о фактическом состоянии летательного аппарата.

Внезапный отказ, обусловленный повреждением или усталостным разрушением элемента, обычно легко выявляется при визуальном контроле.

Коррозия считается актуальной проблемой эксплуатации. В связи с этим по требованиям ИКАО – программы по сохранению целостности конструкции ЛА – обязательно включают программы по предупреждению и контролю уровня коррозии. В частности, программа коррозионной защиты содержит описание методов обнаружения, удаления и предупреждения коррозии. Основным средством обнаружения повреждения вследствие коррозии является визуальный осмотр, для недоступных зон применяются методы неразрушающего контроля [1].

Коррозионные поражения элементов, возникающие в процессе эксплуатации, требуют своевременного обнаружения и устранения. Неудаленные очаги коррозии при дальнейшей эксплуатации развиваются, как правило, без торможения во времени.

Своевременное обнаружение коррозионных поражений при визуальных и инструментальных осмотрах зависит от возможности доступа к осматриваемой зоне и величины (относительного размера) поражения.

Схемы и рисунки элементов конструкции, которые необходимо контролировать по коррозионному состоянию при выполнении технического обслуживания, методы удаления очагов коррозии и восстановления защитных покрытий приведены разработчиком ЛА в руководстве по защите от коррозии летательного аппарата в эксплуатации.

Коррозионные поражения элементов, находящихся в легкодоступных местах, также выявляются при визуальных осмотрах.

Для осмотра труднодоступных зон необходимо использовать переносные лампы, поворотные зеркала, перископические дефектоскопы, эндоскопы и другие инструменты.

При осмотре силовых элементов конструкции с целью контроля коррозионного состояния необходимо через определенные периоды времени применять инструментальные методы неразрушающего контроля.

Для обеспечения полного использования возможностей методов неразрушающего контроля должны выполняться следующие условия: