Атмосферная коррекция гиперспектральных изображений с помощью приближённого решения уравнения переноса MODTRAN
Автор: Белов Александр Михайлович, Мясников Владислав Валерьевич
Журнал: Компьютерная оптика @computer-optics
Рубрика: Анализ гиперспектральных данных
Статья в выпуске: 3 т.38, 2014 года.
Бесплатный доступ
В работе представлен метод атмосферной коррекции гиперспектральных изображений полученных с помощью космической съёмки. Метод основан на приближённом решении уравнения переноса модели MODTRAN с использованием совместного анализа гиперспектрального изображения полученного с помощью космической съёмки и идеального гиперспектрального изображения, свободного от атмосферных искажений.
Гиперспектральное изображение, данные дистанционного зондирования земли, авиационная съёмка, космическая съёмка, спектральный профиль, уравнение переноса, метод наименьших квадратов
Короткий адрес: https://sciup.org/14059267
IDR: 14059267
Текст научной статьи Атмосферная коррекция гиперспектральных изображений с помощью приближённого решения уравнения переноса MODTRAN
Атмосферная коррекция данных дистанционного зондирования Земли (ДЗЗ) является одним из важнейших этапов их предварительной обработки. Отличия детектируемой на борту космического аппарата (КА) освещённости поверхности от истинной зависят от множества факторов : угла склонения солнца, положения и угла съёмки КА, состава и влажности атмосферы и т. д. Все эти факторы учитываются в обобщённом уравнении переноса [1]. Однако даже используя столь детальную модель атмосферы, достаточно сложно точно решить задачу атмосферной коррекции ввиду большого количества неизвестных параметров, значения которых требуют значительного числа наземных и метеорологических наблюдений. Кроме того, в общем случае наблюдаемая поверхность не является ламбертовой, и для моделирования отражающей способности такой поверхности требуется построение двунаправленной функции распределения отражения, что также требует лабораторных исследований структурных и оптических свойств материалов [1].
Проблема атмосферной коррекции данных ДЗЗ становится особенно острой, когда анализ изображений существенным образом опирается на спектральные составляющие регистрируемого излучения. Такая ситуация, например, возникает при обработке и анализе гиперспектральных изображений (ГСИ) ДЗЗ, которым в последнее время уделяется особое внимание. Каждый отсчёт гиперспектрального изображения содержит «спектральный профиль» или «спектральную сигнатуру» соответствующего элемента земной поверхности, по которому собственно и производится такая обработка [2, 3].
В данной работе предложен метод проведения атмосферной коррекции гиперспектральных ДЗЗ, основанный на приближённом решении упрощённого уравнения переноса модели MODTRAN. При таком подходе нет необходимости моделировать атмосферу явным образом, задача сводится к определению неизвестных коэффициентов уравнения, а все тонкости прохождения света через атмосферу остаются в рамках модели. Однако для такого решения требуется идеальное (т.е. свободное от атмосферных искажений)
ГСИ той же местности. В качестве такого изображения предлагается использовать ГСИ, полученные с помощью съёмки с низколетящих летательных аппаратов (ЛА) или со стационарных гиперспектрометров. Очевидно, что для таких изображений атмосферные искажения будут весьма незначительными.
Уравнение переноса модели MODTRAN
MODTRAN – акроним из названия модели атмосферного пропускания для среднего спектрального разрешения (MODerate spectral resolution atmospheric TRANsmittance algorithm and computer model). Это вычислительный алгоритм переноса излучения, который используется для моделирования спектральных характеристик поглощения, передачи, излучения и рассеяния в атмосфере. Модель MODTRAN использует предположение о том, что атмосфера является сферически симметричной и состоит из однородных слоёв, которые характеризуются температурой, давлением и газовым составом. Характеристики этих слоев либо берутся из предопределённой модели атмосферы, либо задаются пользователем по данным радиозондирования и наземных наблюдений.
В модели MODTRAN используется следующее упрощение уравнения переноса [4]:
L =
-PL + BP + l 1 - Рср S 1 - Рср S ‘
где p = p(x, y, %) - коэффициент отражения для пик- селя заданного канала, ρcp – средний коэффициент отражения для пикселя и его ближайшей области, La – яркость, рассеянная атмосферой назад, A, B – коэффициенты, которые зависят от атмосферных условий, S – сферическое альбедо атмосферы. Значения A, B, S, La вычисляются посредством модели MODTRAN [5], однако для точного вычисления этих параметров необходимо иметь модель атмосферы, согласованную с местом, временем и погодными условиями съёмки.
При отсутствии всех необходимых параметров модели атмосферы выполнить атмосферную коррекцию можно посредством приближённого решения уравнения (1). Рассмотрим этот метод подробнее.
Приближённое решение уравнения переноса модели MODTRAN
В пространстве изображения уравнение переноса имеет вид:
L ( i , j )
Ap( i, j ) BPcp (i, j )
I I -L , \2/
1 - Рср (i, j) 5 1 - Рср (i, j) 5 ° где i =1...M, j =1...N - координаты в плоскости изображения.
По точкам идеального ГСИ можем определить р( ij ) и pcp( ij ). По точкам космического ГСИ можем определить L ( i , j ).
Таким образом, необходимо определить четыре неизвестных параметра: A , B , 5 , L a . Нетрудно заметить, что уравнение (2) является квадратичным относительно неизвестных параметров. Однако зафиксировав некоторое значение L * = L * , мы переходим к линейному уравнению относительно неизвестных A , B , 5 .
Таким образом, записав уравнение (2) для каждой пары соответствующих точек авиационного и космического ГСИ, мы получим переопределённую систему из MN линейных уравнений с тремя неизвестными A , B , 5 .
A р ( 1,1 ) + B р cp ( 1,1 ) + 5 р cp ( 1,1 ) 1 L ( 1,1 ) - L* |= L ( 1,1 ) - L* v '
. A р ( 1,2 ) + B р cp ( 1,2 ) + 5 р cp ( 1,2 ) 1 L ( 1,2 ) - L* 1= L ( 1,2 ) - L*
A р ( M , N ) + B р cp ( M , N ) + 5 р cp ( M , N ) [ L ( M , N ) - L* ]= L ( M , N ) - L*
Для определения неизвестных параметров целесообразно воспользоваться методом наименьших квадратов (МНК). Представим систему линейных уравнений в виде следующего приближённого матричного равенства:
Rx = b , (4)
где
■ р ( 1,1 ) р cp ( 1,1 ) р cp ( 1,1 ) ( l ( 1,1 ) - L * ) "
R = р ( 1,2 ) р cp ( 1,2 ) р cp ( 1,2 ) ( l ( 1,2 ) - L * )
_р ( M , N ) р cp ( M , N ) р cp ( M , N ) ( L ( M , N ) - L * )_
A
x =
B
S
L ( 1,1 ) - L *
L ( 1,2 ) - L *
. L ( M , N ) - L *
Понятно, что точного решения такая система не имеет, однако, используя МНК, можем получить приближённое решение в смысле минимального расстояния между векторами Rx и b , для чего необходимо решить следующую задачу минимизации:
J(x) = (Rx-bT(Rx-b)^ min .(5)
Решение этой задачи минимизации приводит к решению следующей системы уравнений:
RT Rx = RTb .(6)
Соответственно решение этой системы определяется выражением вида:
x = (RT R j"1 RTb.(7)
Исходя из определённых выше выражений для R и b , можем записать выражения для RTR и RTb :
RT R =
NM
SS р ( . j ) 2
i = 1 j = 1
NM
SS р ( , j ) р cp ( i, j )
i = 1 j = 1
NM
S S р О , j ) р cp ( i , j )( L ( i,j )- L * ) i = 1 j = 1
S S р ( , у ) р cp ( i,j ) Z S р ( - +) р cp ( i , j ) ( L ( i , j ) - L * )
i = 1 j = 1 i = 1 j = 1
NM NM
SS р cp ( i, j ) 2 SS р cp ( i , j ) 2 ( L ( i , j ) - L * )
i = 1 j = 1 i = 1 j = 1
NM NM
SS р cp ( i , j ) 2 ( l ( i , j ) - L * ) SS р cp ( i , j ) 2 ( L ( i , j ) - L * ) 2 i = 1 j = 1 i = 1 j = 1
RTb =
NM
SS р ( - -, У ) ( L ( i,j ) - L * )
i = 1 j = 1
NM
SS р cp ( i,j )( L ( i , j ) - L * )
i = 1 j = 1
NM
SS р cp ( i,j ) ( L ( i,j ) - L * ) 2
i = 1 j = 1
Теперь рассмотрим вопрос определения фиксированного значения параметра L* = L*. Логично пред- положить, что искомое значение должно принадлежать интервалу [0,min L* (i, j)]. Далее при переборе значений интервала с некоторым шагом AL* для каждого значения L* = kAL*, k eN необходимо найти решение x* системы (6) и рассчитать ошибку функционала (5), которая определяется следующим выражением:
е j ( x ) ( L * ) = J ( x*) =( Rx* - b ) T ( Rx* - b ) . (10)
Соответственно выбирается то значение L a = k A L a , k e N, которое обеспечивает минимум ошибки функционала £ J ( x ) ( L a ). Заметим, что при переборном поиске значения L * a объём вычислений незначителен, т.к., исходя из структуры матриц (8, 9), видно, что все суммы могут быть рассчитаны заранее, а те элементы матриц, которые зависят от L a , корректируются при переборе.
Атмосферная коррекция
Атмосферная коррекция космического гиперспектрального снимка производится согласно формуле [4]:
L - L a + B ( L - L cp ) Р A + В + ( L cp - L * ) S
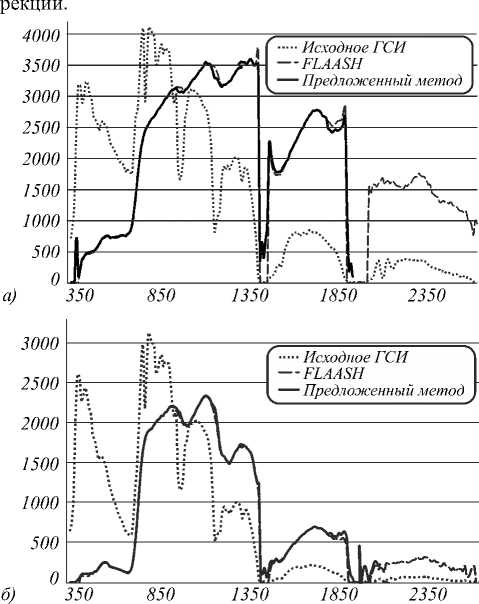
печения ENVI были построены спектральные профили, которые представлены на рис. 2.

где L cp – пространственное усреднение наблюдаемого значения яркости, а смысл остальных параметров аналогичен уравнению (1).
В пространстве изображения уравнение (11) примет вид:
L(i, j)-La + A(L(i, j)-Lcp (i, j))
P =------------- В -----------;-------. (12)
A + B + ( Lcp ( i, j )-La ) S
После нахождения оптимального значения L * a и вектора параметров x =[ A B S ] имеется возможность провести атмосферную коррекцию произвольного гиперспектрального космического снимка, снятого в аналогичных условиях, согласно уравнению (12).
Экспериментальные исследования
Предложенным методом была произведена атмосферная коррекция ГСИ JasperRidge98av.img с ЛА AVIRIS. При проведении атмосферной коррекции для расчёта ρ cp использовалось гауссовское окно размером 51, а для расчёта L cp - гауссовское окно размером 11. В качестве идеального изображения было взято исходное ГСИ, скорректированное с помощью алгоритма FLAASH, который также основан на модели MODTRAN.
На этой паре ГСИ были рассчитаны приближённые значения неизвестных параметров уравнения переноса, по которым впоследствии и проводилась атмосферная коррекция исходного изображения согласно уравнению (12). Также было синтезировано ГСИ поля ошибок, рассчитанного по ГСИ, скорректированному с помощью алгоритма FLAASH, и ГСИ, скорректированному с помощью предложенного алгоритма. Среднее значение относительной среднеквадратичной ошибки, рассчитанной по паре скорректированных ГСИ, по всем спектральным каналам составило 0,022. Результаты проведённой атмосферной коррекции представлены на рис. 1.
По исходному и паре скорректированных ГСИ для некоторых пикселей с помощью программного обес-


Заключение
Экспериментальные исследования показали, что предложенный метод позволяет оценить параметры модели атмосферы и применять их для решения задачи атмосферной коррекции космических ГСИ. Это подтверждается близостью спектральных сигнатур для предложенного метода атмосферной коррекции и алгоритма FLAASH. Ограничение предложенного метода заключается в том, что найденные в результате совместного анализа космического и авиационного ГСИ параметры модели применимы только для атмосферной коррекции космических ГСИ, полученных в схожих условиях съёмки.
В рамках дальнейших исследований данной проблемы целесообразно провести исследования влияния различных типов и размеров окон усреднения для вычисления ρcp и Lcp на качество атмосферной кор-
Работа выполнена при частичной финансовой поддержке:
-
• Министерства образования и науки РФ в рамках реализации мероприятий Программы повышения конкурентоспособности СГАУ среди ведущих мировых научно-образовательных центров на 2013– 2020 годы;
-
• грантов РФФИ, проекты № 13-07-12103-офи-м, 13-01-12080-офи-м, 12-07-00021-а;
-
• программы фундаментальных исследований Президиума РАН «Фундаментальные проблемы информатики и информационных технологий», проект 2.12;
-
• Министерства образования и науки Российской Федерации (в рамках постановления Правительства Российской Федерации от 09.04.2010 г. № 218: договор № 02.Г36.31.0001 от 12.02.2013).


