Атмосферные эффекты мюонной компоненты космических лучей

Автор: Янчуковский В.Л., Кузьменко В.С.

Журнал: Солнечно-земная физика @solnechno-zemnaya-fizika

Статья в выпуске: 3 т.4, 2018 года.

Бесплатный доступ

Вариации интенсивности космических лучей, наблюдаемые в глубине атмосферы, включают атмосферную составляющую вариаций. Мюонные телескопы космических лучей наряду с барометрическим обладают значительным температурным эффектом, обусловленным нестабильностью регистрируемых частиц. Для учета в данных мюонных телескопов атмосферных эффектов по экспериментальным данным с использованием различных методов факторного анализа найдены метеорологические коэффициенты интенсивности регистрируемых в глубине атмосферы мюонов. Полученные по экспериментальным данным результаты сопоставлены с результатами теоретических расчетов.

Космические лучи, мюоны, температура, атмосфера

Короткий адрес: https://sciup.org/142220302

IDR: 142220302 | DOI: 10.12737/szf-43201810

Текст научной статьи Атмосферные эффекты мюонной компоненты космических лучей

Вариации интенсивности космических лучей (КЛ), наблюдаемые в атмосфере с помощью мюонных телескопов, представляют собой суперпозицию эффектов различной природы [Дорман, 1975]. Межпланетная составляющая вариаций интенсивности КЛ обусловлена процессами на Солнце и в межпланетной среде [Дворников и др., 2005], магнитосферная составляющая вызвана возмущениями в магнитосфере [Кичигин и др., 2017], а атмосферные вариации связаны с изменением параметров атмосферы (давления, температуры, влажности, перераспределения масс) [Дорман, 1972]. Атмосферные вариации интенсивности КЛ складываются из барометрического, температурного эффектов и эффекта влажности. Вклад каждого из перечисленных эффектов в атмосферную составляющую вариаций КЛ для разных вторичных компонент неодинаков. Для нуклонной компоненты определяющим является барометрический эффект. Для мезонной компоненты, состоящей из нестабильных частиц, характерен в основном резко выраженный температурный эффект при наличии небольшого барометрического эффекта. Для общей ионизующей компоненты вторичных КЛ наблюдается вклад всех перечисленных эффектов в атмосферные вариации. При использовании результатов наблюдений, проводимых с помощью мюонных телескопов [Янчуковский и др., 2016], следует корректно учитывать в данных вклад атмосферных эффектов. Для этого необходимо оценить воздействие атмосферных параметров на интенсивность мюонов в атмосфере. Интегральный метод, предложенный в [Дорман, 1957], дает возможность учета температурного эффекта интенсивности мюонов от всей атмосферы. Метод предполагает наличие регулярных данных температурного разреза атмосферы и знание распределения плотности температурных коэффициентов для мюонов в атмосфере. Его расчет был выполнен для Новосибирского мюонного телескопа-годоскопа и Якутского подземного комплекса мюонных телескопов [Кузьменко, Янчуковский, 2017]. Однако на практике результаты теоретических расчетов для коррекции данных наблюдений следует использовать с осторожностью, поскольку все расчеты выполняются обычно с теми или иными приближениями [Дорман, Янке, 1971; Berkova et al., 2008; Дмитриева и др., 2009; Кузьменко, Янчуковский,

2017] . Экспериментальная оценка распределения плотности температурных коэффициентов также затруднена, поскольку вариации температуры различных слоев атмосферы коррелированны. Поэтому для экспериментальной оценки температурных коэффициентов интенсивности мюонов по результатам непрерывных наблюдений были использованы различные методы анализа данных.

МЕТОДЫ

Для анализа данных непрерывных наблюдений были использованы методы факторного анализа [Енюков, 1989] : корреляционно-регрессионный анализ [Дрейпер, Смит, 2007; Фёрстер, Рёнц, 1981] и метод главных компонент (ГК) [Айвазян и др., 1989; Айвазян, 2001] .

Вариации интенсивности мюонов y , обусловленные изменениями температуры n слоев атмосферы, представляем в виде линейного уравнения регрессии, в котором температурный эффект интенсивности выражен через переменные x 1 , x 2 , x 3 ,…, xn :

y=a0+a1x1+a2x2+…+anxn+ε или n

Y = A o + ^ A j X j + e.

j = 1

Здесь результативный признак Y = {y1,...,yi,...,ym} — вариации интенсивности мюонов

—

м i

I м

I^м- 100 = 5 1 M i ,

независимые переменные (факторы) Xj={xj1, …, xjm} — изменения температуры j слоя, Ti — Tj = kTi, Aj — коэффициент регрессии, имеющий смысл температурного коэффициента интенсивности мюонов слоя j атмосферы, ε — вектор случайных компонент, который отличает статистические данные от данных, получаемых при аппроксимации. Для опре- деления параметров Aj (j = 0, n) применяют метод наименьших квадратов, который для линейных уравнений регрессии сводится к решению системы нормальных уравнений [Корн, Корн, 1984].

Есть еще один вид уравнения множественной регрессии, которым мы также будем пользоваться — уравнение регрессии в стандартизованном масштабе [Горлач, 2006] . Представим таким образом уравнение (1):

y i = aixu + a2 x 2i + a3 x3i + ... + a „x„i, y — Y xji— Xj в котором yi. = —----; xH =-------

σ Y σ X j

( i = 1, m )

( j = 1, n )

стандартизованные переменные, а стандартизованные коэффициенты регрессии αj находятся из решения системы уравнений:

rYX1 ai + a2 rX 1 X2 + a3 rX1 X 3 + ... + a nrX1 Xn rVY = a.r„ v + a,+arY Y +... + a rY Y YX2 1 X2X1 23X2X3 n X2Xn

< r_YY = a r_Y _r+ a₉ r_{Y Y} + a. + ... + a r_{Y Y} (3)

YX3 1 X3X1 2 X3X2 3n X3Xn rVY = a,rY Y + ar-y у + a.rY Y +... + a„. YXn1XnX12XnX23XnX3n

Здесь r_YXj , r_XjXk — коэффициенты парной линейной корреляции между переменными. Решение системы уравнений (3) проводилось с использованием прямых методов Гаусса, Крамера и Жордана — Гаусса [Ильин, Позняк, 2004; Волков, 1987] . Переход от найденных стандартизованных коэффициентов α j к искомым коэффициентам многофакторной регрессии Aj осуществляется с помощью соотношения

A j = a j ^^-. (4) ^σ X j

Метод главных компонент [Айвазян и др., 1989; Айвазян, 2001] , а также методы проекций на латентные структуры PLS1 и PLS2 [Эсбенсен, 2005; Померанцев, 2014] были рассмотрены нами ранее [Кузьменко, Янчуковский, 2015] для оценки плотности температурных коэффициентов мюонов по экспериментальным данным. Итерационный алгоритм расчета факторов в пространстве ГК для PLS1 и PLS2 был подробно изложен в [Кузьменко, Янчу-ковский, 2015] . Сопоставление результатов, полученных методами МГК, PLS1 и PLS2, показало, что наилучший дает метод PLS2.

Программа The Unscrambler X [ com/rt/Products/Unscrambler/] позволяет считать методом PLS2 с использованием четырех алгоритмов:

NIPALS — нелинейный итеративный алгоритм наименьших квадратов, который обеспечивает обработку в случае отсутствия некоторых значений в данных и подходит для вычисления только первых нескольких факторов из набора данных [Эсбенсен, 2005] ;

ORTHOGONAL SCORES PLS — классический алгоритм PLS с использованием NIPALS, который не обеспечивает обработку при отсутствии некоторых значений в данных [Martens, Naes, 1991] ;

WIDE-KERNEL PLS — алгоритм, который не работает при отсутствии некоторых значений в данных и лучше всего подходит для данных с несколькими образцами и большим количеством переменных [Rannar et al., 1994] ;

KERNEL PLS — алгоритм, который лучше всего подходит для большого количества образцов (тысячи образцов с несколькими переменными) [Lindgren et al., 1993; de Jong, Ter Braak, 1994; Dayal, McGregor, 1997] .

Первые два алгоритма использовались нами ранее [Кузьменко, Янчуковский, 2015] . Третий алгоритм не подходит для данной задачи, поскольку в ней рассматривается набор данных с малым количеством переменных и большим количеством образцов (число образцов означает здесь число значений в рядах данных для каждой переменной). Поэтому в данной работе в расчетах будет использоваться четвертый алгоритм KERNEL PLS.

ИСПОЛЬЗУЕМЫЕ ДАННЫЕ

Созданные программы [Кузьменко, Янчуков-ский, 2015] предназначены для чтения и формирования требуемого формата следующих данных:

• данные аэрологического зондирования (Буг-ринская роща, Новосибирск): температура, скорость и направление ветра на различных изобарических уровнях: 1000, 925, 850, 700, 500, 400, 300, 250, 200, 150, 100, 50 мб [https://ruc.noaa.gov/raobs] ;
• данные наземных измерений интенсивности КЛ: нейтронной компоненты, общей ионизующей компоненты и мюонной компоненты под различными углами к зениту (0°, 30°, 40°, 50°, 60°, 67°, 71°) и азимуту (юго-восток, северо-запад, юго-запад, северо-восток), а также атмосферного давления и температуры приземного слоя (станция КЛ Новосибирск [http://cosm-rays.ipgg.sbras.ru] ). В анализе используются среднесуточные значения данных наблюдений за 2004–2011 гг. Такая дискретизация данных обусловлена периодичностью аэрологического зондирования (12 ч).

МЕТЕОРОЛОГИЧЕСКИЕ КОЭФФИЦИЕНТЫ ИНТЕНСИВНОСТИ МЮОНОВ

Вариации интенсивности мюонов, регистрируемых на уровне h ₀ атмосферы в пункте с порогом геомагнитного обрезания R _c можно представить следующим образом:

- j в м ( h ) dh - 1 1 + ^ м ( T o , h 0 , h ) A T ( h ) dh +

h , J I 0

—м ⁽ ^h 0 Hexp

^J м I

+ J ( R ) W ( R , h 0 ) dR , (5)

Rc D где βм(h) — барометрический коэффициент интенсивности мюонов, wм(T0, h0, h) — функция плотности температурных коэффициентов, отражающая вклад слоев атмосферы в создание интегрального температурного эффекта интенсивности; ΔT(h) — временные вариации температуры атмосферы в зависимости от высоты, (ΔD/D)(R) и W(R, h0) — спектр вариаций первичного потока и коэффициенты связи для мюонной компоненты КЛ соответственно. Здесь R — жесткость первичных частиц, h — атмосферное давление, h0 и T0 — давление и температура атмосферы на уровне наблюдения интенсивности мюонов.

Вариации интенсивности мюонов (5) можно представить также уравнением линейной регрессии, в котором барометрический и температурный эффекты, а также эффект от первичной вариации КЛ выражены через факторы x 1 , x 2 , x 3 , x 4 :

y = a ₀+ a ₁ x ₁+ a ₂ x ₂+ a ₃ x ₃+ a ₄ x ₄+ε. (6)

Результативный фактор y — вариации интенсив-J. - J ности мюонов —м=—-100 = 5J ., фактор Xi — из-Jм м менения атмосферного давления hi–h0=Δhi, фактор x2 — изменения температуры слоя переменной массы (T — Tn)(P, — 950) = Att (p - 950), фактор x3 — изменения среднемассовой температуры атмосферы T - - T = AT фактор X4 — изменения интенсив-cмi cм cмi, 4

N - N ности нейтронной компоненты —i-=—100 = 5ni, обусловленные изменениями спектра первичного потока КЛ.

Уравнение (6) представим в стандартизованном масштабе аналогично выражению (2).

Стандартизованные коэффициенты регрессии находим из решения системы уравнений (3). Затем переходим к искомым коэффициентам многофакторной регрессии, используя соотношение (4). Полученные таким образом коэффициенты представлены в табл. 1.

Полученные результаты позволяют в исходных данных наблюдений выделить непосредственно температурную составляющую вариаций интенсивности мюонов, не прибегая, как это делалось ранее [Кузьменко, Янчуковский, 2015] , к спектрографическому анализу наблюдаемых вариаций [Дворников и др., 1972; Yanchukovsky et al., 2011] .

ПЛОТНОСТЬ ТЕМПЕРАТУРНЫХ КОЭФФИЦИЕНТОВ ИНТЕНСИВНОСТИ МЮОНОВ

Корреляционно-регрессионный анализ . Атмосфера разбивается условно на 11 слоев. Это количество обусловлено аэрологическими данными, которые представлены для 11 изобар: 925, 850, 700, 500, 400, 300, 250, 200, 150, 100 и 50 мб. Поэтому в выражении (2) n =11. Из решения системы уравнений (3) находятся стандартизованные коэффициенты регрессии. С помощью (4) они преобразуются в коэффициенты многофакторной регрессии, имеющие смысл температурных коэффициентов. При переходе к плотности температурных коэффициентов интенсивности мюонов, как и ранее, учитывается весовой коэффициент, обусловленный относительной массой слоя атмосферы A h Kp^ a h i . Здесь A h, = {75, 50, 50, 50, 50, 75, 100,

/ i = 1

150, 175, 125, 50} мб.

Полученные с помощью корреляционно-регрессионного анализа результаты для мюонов, регистрируемых под углами к зениту от 0° до 60°, сведены в табл. 2.

Метод PLS2 с использованием алгоритма KERNEL PLS . Температурные коэффициенты интенсивности мюонов в атмосфере для различных зенитных углов регистрации, найденные методом PLS2 (алгоритм KERNEL PLS), приведены в табл. 3.

При переходе к плотности температурных коэффициентов интенсивности мюонов, как и ранее, учитывается относительная масса Δ h слоя атмосферы.

Полученные методом PLS2 плотности температурных коэффициентов интенсивности мюонов представлены в табл. 4.

Выбор количества главных компонент от 1 до 3 незначительно влияет на полученный результат. При числе главных компонент более трех имеют место потеря информации в исходных данных и нефизическая динамика результирующих кривых.

ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

Полученные результаты представлены для сопоставления на рис. 1 и 2. На рис. 1 показаны распределения плотности температурных коэффициентов интенсивности мюонов, регистрируемых с вертикального

Таблица 1

Коэффициенты многофакторной регрессии

A j	Угол к зениту θ, град
A j	O.I.	0	30	40	50	60	67	71
A 1 , %/мб	–0.185	–0.158	–0.158	–0.158	–0.173	–0.186	–0.245	–0.3
	±0.025	±0.027	±0.029	±0.032	±0.034	±0.056	±0.061	±0.064
A 2 , %/°С,	–0.0283	–0.065	–0.0652	–0.0643	–0.066	–0.065	–0.068	–0.07
10-2	±0.0056	±0.0046	±0.0042	±0.038	±0.0048	±0.0058	±0.0072	±0.009
A 3 , %/°С	–0.227	–0.228	–0.228	–0.242	–0.256	–0.262	–0.308	–0.31
	±0.023	±0.025	±0.024	±0.028	±0.031	±0.035	±0.042	±0.052
A ₄	0.381	0.383	0.356	0.329	0.288	0.260	0.260	0.260
	±0.0302	±0.0306	±0.0275	±0.0268	±0.0246	±0.034	±0.046	±0.052

Здесь A 1 — барометрический коэффициент, A 2 — температурный коэффициент слоя переменной массы (приземного слоя), A 3 — температурный коэффициент от среднемассовой температуры атмосферы и A 4 — коэффициент регрессии с данными нейтронного монитора для интенсивности мюонов, регистрируемых без свинцового экрана (O.I.) и со свинцовым экраном под углами к зениту в 0, 30, 40, 50, 60, 67 и 71°.

Таблица 2

Плотность температурных коэффициентов интенсивности мюонов в атмосфере w ( h ), полученных с помощью корреляционно-регрессионного анализа

Глубина атмосферы h , мб	Угол к зениту θ, град
Глубина атмосферы h , мб	O.I.	0	30	40	50	60
50	–0.152	–0.245	–0.250	–0.190	–0.190	–0.348
50	±0.0605	±0.0975	±0.0985	±0.0703	±0.0804	±0.0909
100	–0.385	–0.501	–0.538	–0.348	–0.649	–0.484
100	±0.0723	±0.0939	±0.0935	±0.0731	±0.0957	±0.0913
150	–0.344	–0.659	–0.626	–0.626	–0.728	–0.637
150	±0.0417	±0.0798	±0.1217	±0.0703	±0.0806	±0.0879
200	–0.399	–0.537	–0.538	–0.503	–0.856	–0.565
200	±0.0589	±0.0794	±0.1184	±0.0982	±0.0987	±0.0949
250	–0.184	–0.193	–0.153	–0.330	–0.237	–0.252
250	±0.0738	±0.0798	±0.0696	±0.0830	±0.0906	±0.0266
300	–0.164	–0.194	–0.238	–0.235	–0.272	–0.325
300	±0.0712	±0.0844	±0.0853	±0.0906	±0.0948	±0.1056
400	–0.235	–0.235	–0.258	–0.310	–0.284	–0.310
400	±0.0820	±0.0820	±0.0920	±0.0932	±0.0953	±0.1092
500	–0.195	–0.283	–0.298	–0.318	–0.325	–0.395
500	±0.0681	±0.0988	±0.117	±0.127	±0.0975	±0.136
700	–0.275	–0.371	–0.325	–0.355	–0.385	–0.260
700	±0.0825	±0.111	±0.0990	±0.136	±0.0979	±0.1054
850	–0.225	–0.315	–0.363	–0.283	–0.450	–0.340
850	±0.0602	±0.0948	±0.113	±0.0909	±0.0938	±0.1077
925	–0.279	–0.381	–0.506	–0.351	–0.630	–0.500
925	±0.0599	±0.0818	±0.150	±0.123	±0.145	±0.147

Таблица 3

Температурные коэффициенты интенсивности мюонов, найденные методом PLS2 (алгоритм KERNEL)

Глубина атм-ры h , мб	Угол к зениту θ, град
Глубина атм-ры h , мб	0	30	40	50	60	67	71	O.I.
50	–0.0470	–0.0471	–0.0475	–0.0567	–0.0503	–0.0570	–0.0388	–0.0384
50	±0.0034	±0.0072	±0.0036	±0.0061	±0.0053	±0.0072	±0.0161	±0.0034
100	–0.0392	–0.0392	–0.0395	–0.0472	–0.0419	–0.0475	–0.0323	–0.0320
100	±0.0023	±0.0054	±0.0043	±0.0048	±0.0044	±0.0046	±0.0125	±0.0023
150	–0.0324	–0.0324	–0.0327	–0.0391	–0.0346	–0.0392	–0.0267	–0,0264
150	±0.0017	±0.0042	±0.0037	±0.0030	±0.0031	±0.0041	±0.0110	±0.0017
200	–0.0299	–0.0300	–0.0302	–0.0361	–0.0320	–0.0363	–0.0247	–0.0244
200	±0.0020	±0.0044	±0.0037	±0.0039	±0.0031	±0.0036	±0.0098	±0.0020
250	–0.0276	–0.0276	–0.0278	–0.0333	–0.0295	–0.0334	–0.0227	–0.0225
250	±0.0018	±0.0042	±0.0035	±0.0035	±0.0031	±0.0041	±0.0090	±0.0018
300	–0.0214	–0.0214	–0.0216	–0.0258	–0.0228	–0.0259	–0.0176	–0,0174
300	±0.0023	±0.0041	±0.0042	±0.0030	±0.0036	±0.0046	±0.0074	±0.0023
400	–0.0160	–0.0160	–0.0162	–0.0193	–0.0171	–0.0194	–0.0132	–0.0131
400	±0.0028	±0.0045	±0.0042	±0.0030	±0.0040	±0.0051	±0.0067	±0.0029
500	–0.0144	–0.0144	–0.0145	–0.0174	–0.0154	–0.0175	–0.0119	–0.0118
500	±0.0034	±0.0057	±0.0058	±0.0052	±0.0053	±0.0072	±0.0067	±0.0034
700	–0.0160	–0.0160	–0.0161	–0.0193	–0.0171	–0.0194	–0.0132	–0.0130
700	±0.0032	±0.0049	±0.0048	±0.0039	±0.0036	±0.0056	±0.0067	±0.0032
850	–0.0155	–0.0156	–0.0157	–0.0187	–0.0166	–0.01883	–0.0128	–0.0127
850	±0.0032	±0.0049	±0.0050	±0.0039	±0.0044	±0.00513	±0.0067	±0.0032

Таблица 4

Плотность температурных коэффициентов по методу PLS 2 (алгоритм KERNEL)

Глубина атм-ры h , мб	Угол к зениту θ, град
Глубина атм-ры h , мб	0	30	40	50	60	67	71	O.I.
50	–0.580	–0.581	–0.585	–0.700	–0.620	–0.703	–0.479	–0.474
50	±0.041	±0.089	±0.044	±0.075	±0.066	±0.088	±0.198	±0.041
100	–0.725	–0.726	–0.731	–0.874	–0.775	–0.879	–0.598	–0.592
100	±0.043	±0.099	±0.080	±0.088	±0.082	±0.085	±0.232	±0.043
150	–0.599	–0.600	–0.604	–0.723	–0.640	–0.726	–0.494	–0.489
150	±0.031	±0.077	±0.068	±0.056	±0.057	±0.076	±0.203	±0.031
200	–0.554	–0.555	–0.559	–0.668	–0.592	–0.671	–0.457	–0.452
200	±0.037	±0.081	±0.068	±0.072	±0.057	±0.066	±0.181	±0.037
250	–0.510	–0.511	–0.515	–0.616	–0.546	–0.619	–0.421	–0.417
250	±0.034	±0.078	±0.065	±0.064	±0.057	±0.076	±0.167	±0.034
300	–0.263	–0.264	–0.266	–0.318	–0.282	–0.319	–0.217	–0.215
300	±0.029	±0.050	±0.051	±0.037	±0.044	±0.057	±0.092	±0.029
400	–0.148	–0.148	–0.150	–0.179	–0.159	–0.180	–0.122	–0.121
400	±0.026	±0.041	±0.039	±0.028	±0.037	±0.047	±0.062	±0.026
500	–0.089	–0.089	–0.090	–0.107	–0.095	–0.108	–0.073	–0.073
500	±0.021	±0.035	±0.036	±0.032	±0.033	±0.047	±0.041	±0.021
700	–0.084	–0.085	–0.085	–0.102	–0.090	–0.102	–0.070	–0.069
700	±0.017	±0.026	±0.025	±0.021	±0.019	±0.030	±0.035	±0.017
850	–0.115	–0.115	–0.116	–0.139	–0.123	–0.139	–0.095	–0.094
850	±0.024	±0.036	±0.037	±0.029	±0.033	±0.038	±0.049	±0.024
925	–0.313	–0.314	–0.316	–0.378	–0.335	–0.380	–0.258	–0.256
925	±0.067	±0.093	±0.111	±0.087	±0.099	±0.133	±0.138	±0.067

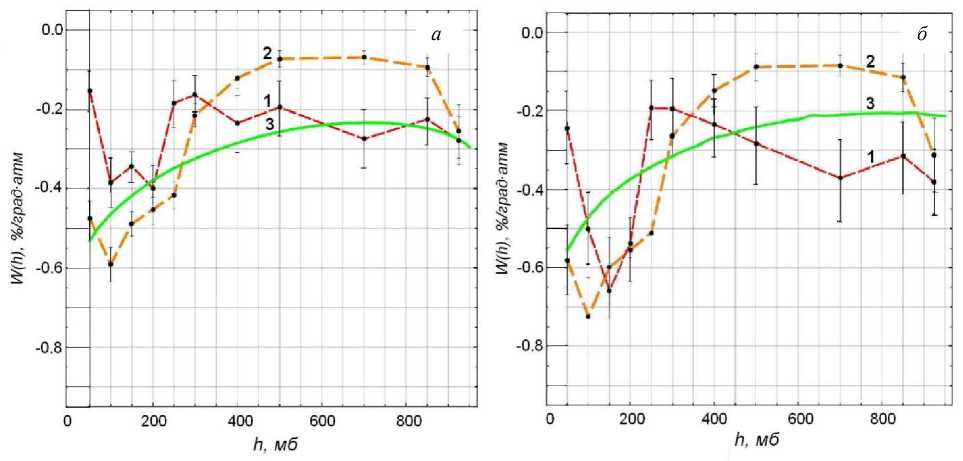
Рис. 1. Распределение плотности температурных коэффициентов интенсивности мюонов, регистрируемых на уровне моря под зенитным углом в 0° без экрана ( а ) и с экраном (Ае=0.56 ГэВ) ( б )

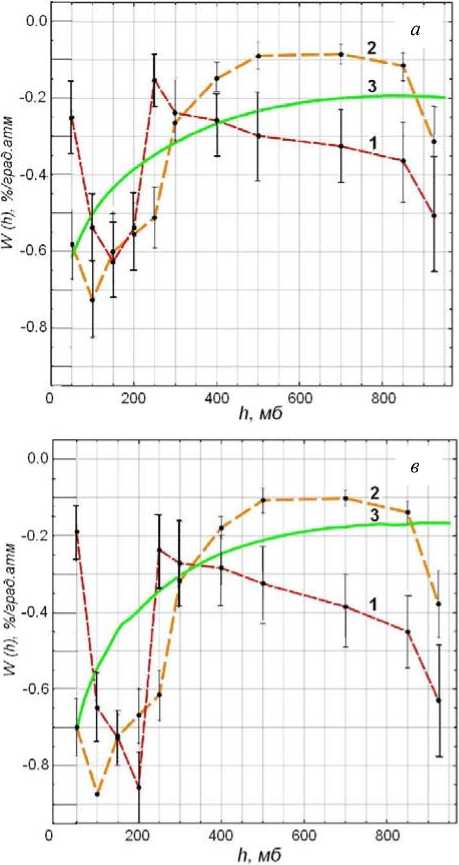
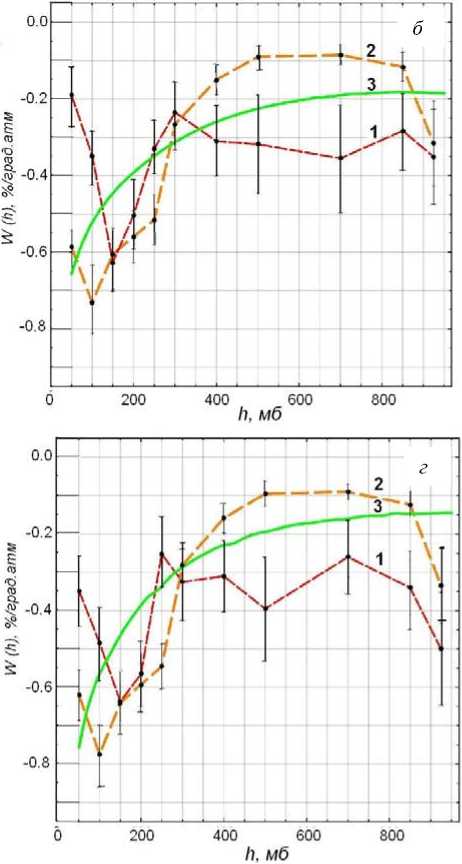
Рис. 2. Распределение плотности температурных коэффициентов интенсивности мюонов, регистрируемых на уровне моря под зенитными углами 30° ( а ), 40° ( б ), 50° ( в ) и 60° ( г )

направления (под углом 0° к зениту) без экрана (рис. 1, а ) и с экраном 0.56 ГэВ (рис. 1, б ).

На рис. 2 приведены распределения плотности температурных коэффициентов для мюонов, регистрируемых под различными углами к зениту: 30° ( а ), 40° ( б ), 50° ( в ) и 60° ( г ).

Представленные распределения получены разными методами: по экспериментальным данным с использованием корреляционно-регрессионного анализа (кривая 1), методом ГК PLS2 (кривая 2), с помощью теоретических расчетов (кривая 3). До глубин <400 мб результаты двух методов в пределах ошибок совпадают. Различия начинаются на глубинах >400 мб. Это можно объяснить тем, что метод PLS2 при выборе оптимального числа главных компонент учитывает статистическую значимость переменных в суммарном эффекте. Метод PLS2 (алгоритм KERNEL) позволяет по экспериментальным данным находить температурные коэффициенты интенсивности мюонов с большей точностью по сравнению с корреляционно-регрессионным анализом. Теоретически рассчитанные распределения имеют лучшее согласие с найденными методом PLS2 (алгоритм KERNEL) при следующих значениях исходных параметров: L p =70 г/см², l π =110 г/см², γ=2.75. Здесь L p — пробег поглощения протонов, l π — пробег поглощения пионов, γ — показатель степенного спектра первичного потока космических лучей.

ЗАКЛЮЧЕНИЕ

Экспериментальная оценка распределения плотности температурных коэффициентов обычно затруднена, поскольку вариации температуры различных слоев атмосферы коррелированны. Показано, что для экспериментальной оценки температурных коэффициентов интенсивности мюонов по результатам непрерывных наблюдений более эффективным и более точным является метод главных компонент PLS2 (алгоритм KERNEL) по сравнению с методами многофакторной регрессии.

В работе использованы экспериментальные данные УНУ «Российская национальная сеть станций космических лучей».

Список литературы Атмосферные эффекты мюонной компоненты космических лучей

Айвазян С.А. Прикладная статистика и основы эконометрики. М.: Юнити, 2001. 403 с.
Айвазян С.А., Бухштабер В.М., Енюков И.С., Мешалкин Л.Д. Прикладная статистика. Классификация и снижение размерности. М.: Финансы и статистика, 1989. 607 с.
Волков Е.А. Численные методы. М.: Физматлит, 1987. 367 с.
Горлач Б.А. Математика. М: Наука, 2006. 911 с.
Дворников В.М., Дорман Л.И., Лузов А.А. и др. Анализ вариаций космических лучей магнитосферного и межпланетного происхождения по данным спектрографа//Изв. АН СССР. Сер. физ. 1972. Т. 36, № 11. С. 2427-2434.
Дворников В.М., Сдобнов В.Е., Кравцова М.В. Модуляция космических лучей регулярными электромагнитными полями гелиосферы в период солнечных протонных событий//Изв. РАН. Сер. физ. 2005. Т. 69, № 6. С. 821-824.
Дмитриева А.Н., Кокоулин Р.П., Петрухин А.А., Тимашов Д.А. Температурные коэффициенты для мюонов под различными зенитными углами//Известия РАН. Серия физическая. 2009. Т. 73, № 3. С. 371-374.
Дорман Л.И. Вариации космических лучей. М.: Гостехиздат, 1957. 285 с.
Дорман Л.И. Метеорологические эффекты космических лучей. М.: Наука, 1972. 211 с.
Дорман Л.И. Экспериментальные и теоретические основы астрофизики космических лучей. М.: Наука, 1975. 462 с.
Дорман Л.И., Янке В.Г. К теории метеорологических эффектов космических лучей//Изв. АН СССР. Сер. физ. 1971. Т. 35, № 12. С. 2556-2570.
Дрейпер Н., Смит Г. Прикладной регрессионный анализ. Множественная регрессия. 3-е изд. М.: Диалектика, 2007. 912 с.
Енюков И.С. Факторный, дискриминантный и кластерный анализ. М.: Финансы и статистика, 1989. 215 с.
Ильин В.А., Позняк Э.Г. Линейная алгебра: Учебник для вузов. 6-е изд. М.: Физматлит, 2004. 280 с.
Кичигин Г.Н., Кравцова М.В., Сдобнов В.Е. Параметры токовых систем в магнитосфере по данным наблюдений космических лучей в период магнитной бури в июне 2015 г.//Солнечно-земная физика. Т. 3, № 3. С. 15-19
DOI: 10.12737/szf-33201702
Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука, 1984. 831 с.
Кузьменко В.С., Янчуковский В.Л. Определение плотности температурных коэффициентов для мюонов в атмосфере//Солнечно-земная физика. 2015. Т. 1, № 2. С. 91-96
DOI: 10.12737/10403
Кузьменко В.С., Янчуковский В.Л. Распределение плотности температурных коэффициентов для мюонов в атмосфере//Солнечно-земная физика. 2017. Т. 3, № 4. С. 104-116
DOI: 10.12737/szf-34201710
Померанцев А.Л. Хемометрика в Excel: учебное пособие. Томск: Из-во ТПУ, 2014. 435 с.
Фёрстер Э., Рёнц Б. Методы корреляционного и регрессионного анализа. М.: Финансы и статистика, 1981. 302 с.
Эсбенсен К. Анализ многомерных данных. Избранные главы. Черноголовка: Изд-во ИПХФ РАН, 2005. 160 с.
Янчуковский В.Л., Григорьев В.Г., Крымский Г.Ф. и др. Приемные векторы мюонного телескопа станции космических лучей «Новосибирск»//Солнечно-земная физика. 2016. Т. 2, № 1. С. 76-87
DOI: 10.12737/16762
Berkova M.D., Belov A.V., Eroshenko E.A., Yanke V.G. Temperature effect of the muon component of cosmic ray and practical possibilities of its accounting//Proc. 21st ECRS. Kosice, Slovakia, 9-12 September 2008. 2008. P. 123-126.
Dayal, B.S., McGregor J.F. Improved PLS Algorithms//J. Chemometrics. 1997. V. 11. P. 73-65.
de Jong S., Ter Braak C. Comments on the PLS kernel algorithm//J. Chemometrics. 1994. V. 8. P. 169-174.
Lindgren F., Geladi P., Wold S. The kernel algorithm for PLS//J. Chemometrics. 1993. V. 7. P. 45-59.
Martens H., Naes T. Multivariate Calibration. Chichester, UK: John Wiley and Sons, 1991.419 р.
Rannar S., Lindgren F., Geladi P., Wold S. A PLS kernel algorithm for data sets with many variables and fewer objects. Pt. 1: Theory and algorithm // J. Chemometrics. 1994. V. 8. P. 111-125.
Yanchukovsky V.L., Kuz’menko V.S., Antsyz E.N. Results of cosmic ray monitoring with a multichannel complex // Geomagnetism and Aeronomy. 2011. V. 51, N 7. P. 893-896.
URL: http://cosm-rays.ipgg.sbras.ru (дата обращения 23 ноября 2017 г.).
URL: https://ruc.noaa.gov/raobs (дата обращения 17 февраля 2017 г.).
URL: http://www.camo.com/rt/Products/Unscrambler/unscrambler.html (дата обращения 17 февраля 2017 г.).

Еще

Статья научная