Atomic displacement energy in amorphous compounds

The development of strict physical theories for disordered structures, based on the first principles of statistical physics and quantum mechanics, encounters serious difficulties [1-3]. Approximate model approaches to liquids and amorphous solids thus remain topical at this stage. Among the developments in recent years for disordered glass-like systems are those with respect to the model of delocalized atoms [4-5] with a certain liquid-glass transition interpretation, an original temperature dependence for the viscosity of glass-forming liquids, and the glass plasticity effect. Further development of the model is associated with the search of different methods for calculating the parameters of this model and ascertaining their physical meaning.

This work is devoted to one way of estimating the atomic displacement energy in amorphous compounds and verifying its constancy in a wide range of temperatures (for examples of sheet and lead-silicate glasses).

Analytical approach

The delocalization of an atom in inorganic glasses and their melts is understood as the critical displacement of a bridging atom (e.g., the oxygen atom in a Si–O–Si bridge) due to the local low-activation viscoelastic strain of a network of valence bonds. The latter promotes the formation of elementary volume Δve required for the delocalization of an atom in its neighborhood. The probability of the delocalization of anactive (excited) atom — its displacement from an equilibrium position — is confined to the probability of an elementary fluctuation volume equal to Δve or exceeding it forming near this atom. Delocalization energy Δεe of an atom is equal to the work needed to displace it from an equilibrium position against internal molecular pressure pi produced by interatomic (intermolecular) attraction forces:

A^ , = p i A V e

The molecular mobility typical of delocalized atoms is determined by the fluctuation volume fraction in an amorphous compound (Δ V e ) as

A V_e V ^,

A Ve = Ne AV e , where Ne is the number of delocalized atoms, and V is the volume of an amorphous compound.

In the model of delocalized atoms, the glass transition of a liquid is explained by a drop in the fluctuation volume fraction to a certain minimum value f g , at which the delocalization of an atom is frozen (stopped) [4, 5]:

„ (A V ^

f = —e    ® const « 0.020 - 0.030.

g I V ) T = T

Here, T g is the glass transition temperature corresponding to ultimate viscosity η g ≈ 10¹² Pas. The relative number of delocalized (bridging) atoms N e / N responsible for the viscous flow of glass-forming melts above T g falls to a negligible value of ~ 3% in the glass transition range, which is equivalent to freezing. The delocalization of an atom gradually speeds up as the glass is heated in the region of its softening, and the number of delocalized atoms grows from few in the frozen state to their concentration corresponding to a liquid.

The delocalization energy of an atom is normally calculated using the formula (where R is the universal gas constant) [4]

^A^ e = ^RTg ln1 f g

For the example of alkali-silicate glasses, for which T g ≈ 700 K and f g ≈ 0.025, we have

A ^, ~ 21 kJ/mol.

At first glance, it appears from Eq. (3) that this value of Δεe corresponds only to glass transition temperature Tg, and it must differ from the values at Tg for a different temperature. However, it follows from definition (1) that the delocalization energy of an atom must remain constant in a rather wide range of temperatures, since elementary volume Δve is determined by the volume of a bridging atom (Δve ≈ const), and internal pressure pi is governed by the short-range order (pi ≈ const).

To reach our objective, let us use the equation for the free activation energy of the viscous flow of a glass-forming liquid Δ F η ( T ) [6]

A. AF ■ RT

—

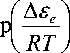
where Δ F ∞ is the potential for the migration of an atom (a kinetic unit) to a new position, and the second summand represents the local structural transformation potential Δ F S ( T )

The idea of dividing the free activation energy Δ F η ( T ) into two components, one of which is constant and the other is a function of the temperature and represents the energy required to change the mutual orientation of groups of atoms, was suggested by Filipovich and Kalinina [3]. This idea has gained further development in the Nemilov valence-configuration theory [3] for the viscous flow of a glass-forming melt. In contrast to Eq. (5), give no explicit form of the temperature dependence of the second summand in the formula for the free flow activation energy. Equation (5) was derived by assuming [6] that the probability of the transition of kinetic unit W from one equilibrium position to another is determined primarily by the probability of a local transformation in the structure of kinetic unit W 1 , and then by probability W 2 that it has sufficient energy Δ F ∞ for migration to a new position; i.e., W = W 1 W 2 . A local structural transformation upon the activation of the viscous flow of a glass-forming melt is described as the delocalization of an atom due to the displacement of neighboring particles and the transformation of their configuration.

Atomic delocalization energy Δε e in Eq. (5) acts as a constant at least in the temperature regions where this relationship describes temperature dependence Δ F η ( T ). To confirm this (and thus validate Eq. (5)), we express Δε e from Eq. (5) as

Age = RT lnl

^{A F} n

—

A F

RT

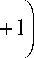
and perform our calculations in a wide range of temperatures. To calculate Δε e by this equation, we must know parameters Δ F η ( T ) and Δ F ∞ . The free activation energy of a viscous flow can be determined from the familiar Eyring equation and viscosity η( T ) as

AF = RT [ln n(T) — ln% ]

Preexponential factor η 0 is found by extrapolating viscosity curve log η –1/T to elevated temperatures T → ∞ using the Lagrangian polynomial in.

Atom migration potential Δ F ∞ represents the hightemperature limit of free flow activation energy Δ F ∞ = Δ F η ( T → ∞) and does not depend on the temperature. It can be calculated from parameters С 1 and С 2 of the Willams-Landel-Ferry (WLF) equation [7] describing the temperature dependence of viscosity η( T ) (and the relaxation time) in the glass transition region, i.e.,

A F   RC i C 2                                (9)

The WLF equation parameters for sheet silicate glass are С 1 = 36.5 and С 2 = 305 K, which yield atom migration potential

\F, = 92.6 kJ/mol.                         (10)

The error in calculating Δ F η and Δ F ∞ is ∼ 3–4% (Table).

Table

Free viscous flow activation energy and atomic delocalization energy Δε e in sheet silicate glass*

Т , К	logη [P]	log(η/η 0 )	Δ F η	Δ ε e
			kJ	/mol
778	15,5	17,47	262	21
787	15	16,97	257	21
805	14	15,97	247	21
816	13,5	15,47	243	21
825	13	14,97	238	21
846	12	13,97	226	21
873	11	12,97	218	21
906	10	11,97	209	21
944	9	10,97	199	21
988	8	9,97	190	21
1039	7	8,97	180	21
1103	6	7,97	169	20
1191	5	6,97	160	20
1313	4	5,97	152	20
1481	3	4,97	142	20
1578	2,5	4,47	136	19

Free viscous flow activation energy and atomic delocalization energy Δε e in sheet silicate glass*

Substituting Δ F η ( T ) and Δ F ∞ from Eqs. (8) and (10), respectively, into Eq. (7), we calculated atomic delocalization energy Δε e ( T ) for this glass in the temperature range of 778–1578 K. As can be seen from the table, energy Δε e required for the delocalization of an atom proves to be constant (Δε e ≈ 21 kJ/mol) in the glass transition region ( T g = 807 K) over a rather wide range of temperatures, in satisfactory agreement with calculations using Eq. (3) (see Eq. (4)). The value of Δε e falls slightly, from 21 to 19 kJ/mol, but at much higher temperatures (1100–1160 K) (Table). It seems that the short-range order starts to change at such elevated temperatures, reducing internal pressure p i in the formula for atomic delocalization energy Δε e (Eq. (1)).

Similar results were obtained for PbO–SiO 2 leadsilicate glass with 49.54 mol % of PbO [13]. The atomic delocalization energy for this glass remains constant (Δε e ≈ 19 kJ/mol) over a wide range of temperatures (682–1276 K) (see figure). The characteristics of this glass are T g = 676 K, log η g [P] = 13.8, ΔF ∞ = 50.2 kJ/mol, log η 0 [P] = –3.2, C 1 = 36.9 and C 2 = 163.4 K.

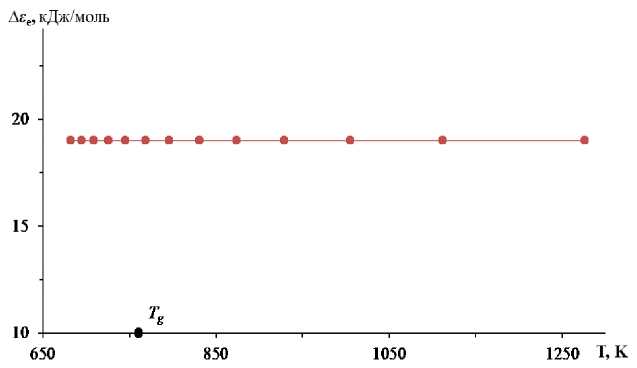
Atomic delocalization energy in lead-silicate glass as a function of temperature [13]

Сonclusions

Atomic delocalization energy Δε e in glasses of silicate and its melts is virtually independent of temperature in a rather wide range in the glass transition region. We believe such constancy in the value of Δε e is also typical of other amorphous compounds. It follows that energy Δε e , calculated using the model of delocalized atoms (Eq. (3)), is valid not only at the glass transition temperature, but at other temperatures of the above region as well.

Acknowledgments

This work was financially supported by the RF Ministry of Education and Science, grant no. 3.5406.2017/8.9.

The authors thank Mashanova A. A. for help in preparing and arranging the work.