Automated Evaluation of Learner’s Solutions Expressed in a Graphical Language: Application to the Relational Databases Domain

Published Online January 2015 in MECS DOI: 10.5815/ijmecs.2015.01.02

The use of graphics in teaching software brings a considerable help. Students learn best by seeing the value and importance of the information presented in the classroom [1]. Hence, for the learners, it is more amusing to handle graphical objects to write texts or formulas. In addition, it is proven that learning is easier with graphs or drawings and is encouraging active processing [2]. The chart brings also a better legibility. Hence, as proposed by

Larkin and Simon in [3], “a diagram is (sometimes) worth ten thousand words”. When one speaks about the use of graphics in teaching, geometry domain is the most important field in which different tools were dedicated. However, this is not the case for the relational data bases domain for which there are fewer tools, generally for physical relational databases languages. Today this domain becomes among the transversal competences or a "life skill" because the use of databases is almost general.

The goal of an automated analysis of learners’ solutions is to have data-processing programs able to evaluate. However, since we can never have the complete valuable evaluation, the interesting thing is to get a formative and helpful one for the learner’s progression. Indeed, when a learner builds his/her solution freely for an open question, he/she can propose a good solution which does not resemble the preregistered ones. This is the main weakness of the diagnosis approach through matching.

In the ODALA framework, the diagnosis is based on the recognition of errors connected to the other components of the semantics discipline represented as domain ontology. More than a simple analysis, ODALA proposes an evaluation process that gives different formative indicators about the learner’s progression that update the learner’s model with new profiles.

• •    There are various languages for the algebraic expressions. Teachers can use different bibliographic references; yet, students, particularly the beginners, don’t always follow these differences.

• •    Among the detected errors by the RDB-E-Learn prototype developed and evaluated in our precedent works, the form errors about the algebraic language must be corrected before starting the semantic analysis. This requires the didactics which imposes the mastery of the language before mastering the logic of building queries.

• •    In some cases, the form errors in the learner’s solution leads to other non committed errors (concerning the form or the semantic) which can cause inconsistencies in the error diagnosis process.

• •    When we studied, along several years, the weaknesses of RDB students, we found that the most popular ones are related to the algebraic operators’ combinations and use. Generally, those who have already understood the “how” to write queries in algebraic languages, found the use and translation to SQL language easy. In addition, when we proposed to students, during the directed working sessions, to write queries with algebraic trees, algebraic expressions or SQL, most of the beginners always chose algebraic trees.

Hence, we see that a self-learning tool for editing and analyzing algebraic trees can be helpful for beginners as support for real class courses, particularly in the case of large number of students. Among the advantages of the graphical representations of queries when learning relational databases (RDB), we have:

• •    A decrease in the complexity of algebraic operators use in queries for novice learners.

• •    A Fast understanding of operators’ combination.

• •    A facility for query optimization notion learning

Writing and translating queries to SQL or another physical level language is not a priority for our tool at this stage. The two principal objectives of the work presented in this article are:

• •    To get algebraic trees construction assisted by a graphic tool adapted for the relational algebraic trees formalism.

• •    To analyze the trees built by learners. This will consist essentially, at this step of our work, of a semantic analysis as recommended in the ODALA approach.

After an overview about self-learning using graphical tools, our proposals relating to the edition and the semantic analysis of algebraic trees are given by the third point. Then, the evaluation of our proposals within a prototype development and use is discussed in the fourth point. We conclude our study with a synthesis about our contribution and our research prospects.

• II.    Self-Learning Using Graphical Tools

A graphic diagram is a visual and semantic representation which illustrates the relations between the facts, the terms and the ideas within a learning process. The graphic diagrams are sometimes called geometrical forms. Teaching using graphs means the representation of some structural or didactical components by graphs.

• •    Geometry Tutor [6] is the first and well referenced system dedicated for self learning of geometry. It is based on proof representation using ideal and buggy rules. After that, different tools for geometry learning were proposed.

• •    Aplusix [7] is a learning environment for algebra in which a pupil develops his own calculations. It is equipped with functions for the representation of the mathematical expressions by trees for a better visualization of the algebraic reasoning carried out by learning.

• •    Diagram [8] is a learning environment for object-oriented modeling (OOM) with UML class diagrams. Its interface includes methodological help, encourages self-correcting and self-monitoring, and provides the learner with specific graphic tools. Diagram includes a diagnosis module that compares the student diagram with a reference diagram. The differences that are noticed in the student diagram give rise to feedbacks.

• •    JRS [9] is a graphical editor of query plans. It is used to define and execute queries on a database represented by two kinds of trees: A logical plan of relational algebra and a physical plan that describes an algorithm to execute a query using the physical operators of the relational DBMS developed in Java as a teaching tool.

• •    RALT [10] allows the creation of relational algebra queries by using a graphical interface following a data flow approach without the need to manually enter the queries into the system.

The works about JRS and RALT are interesting and close to our problematic. However, we find them somehow complicated tools for beginners. In addition, the learner’s solution is, in the end, analyzed by a relational system such as SQL or another relational DBMS’ languages. Also, the graphical constructions used to describe the “logical” plan (seen in JRS) of a query, is different from the algebraic trees commonly taught as the relational queries formalism.

In what follows, we propose a simple editor for a beginner to build a solution to a query generated according to the learner’s profile and the taught concepts in the relational databases discipline. Then, the solution or the tree analysis objective, in this framework, is not to get a concrete manipulation of the database. It is, first, to detect possible errors connected to domain notions and then show them to the learner in a simple and comprehensible way so that he/she can avoid them in the future sessions. If the tree built is correct according to the analyzer, we can then think to translate it to SQL or other relational language and execute it as it is the case in the JRS system. The work presented in this paper is concerned with the edition and the analysis of algebraic trees according to the defined discipline knowledge base (generated from onto-TDM domain ontology) and the ODALA approach for learner’s solutions’ analysis. The following point describes the proposed algebraic trees editor with the semantic analysis option.

• III.    Edition And Semantic Analysis Of Algebraic Trees

• •    the algebraic expressions mode,

• •    the algebraic trees mode

• •    and the SQL mode.

“Fig. 1” shows the learner’s space for an exercise session after an exercise generation and the algebraic trees mode selection for the input of the solution to the query posted in the left window.

• A.    Editing an Algebraic Tree

The algebraic trees editor is used to input a query to the current exercise, displayed in the left side as shown by “Fig. 1”; with the RA trees formalism. This editor (cf. “Fig. 2”) allows to:

• •    Draw an RA tree by using the buttons in the left panel corresponding respectively to the algebraic operators such as: selection, projection, join, union, difference, left join, right join, theta join … The learner clicks on the button corresponding the symbol that he/she wants to draw, then selects, in the drawing window, where to place it. There are also buttons to: draw connections between operators, input a “Text” which can be the operator’s parameters such as the projection attributes names, or an input relation name…

• •    Erase all the drawings so that we can have a cleared page by using the button "Erase all".

• •    Save and restore a drawing using, in the background, the digitalization process. Indeed this starts when the learner clicks on the buttons of the panel and is materialized when he/she clicks on the button “save”. Then, a named instance of a vector is saved in the disk with adequate values corresponding to the tree built in the drawing window. This vector is a data structure defined as a table of records. Each record corresponds to a form defined in the panel with specific parameters in addition to the location attributes. It is on this suggested digitalization that the save/open options and the tree analysis discussed in the next point are based.

• •    Analyze the tree with the “evaluer” option.

• •    Show, under a given pedagogical conditions, fixed by the tutor or teacher, a preregistered solution.

  

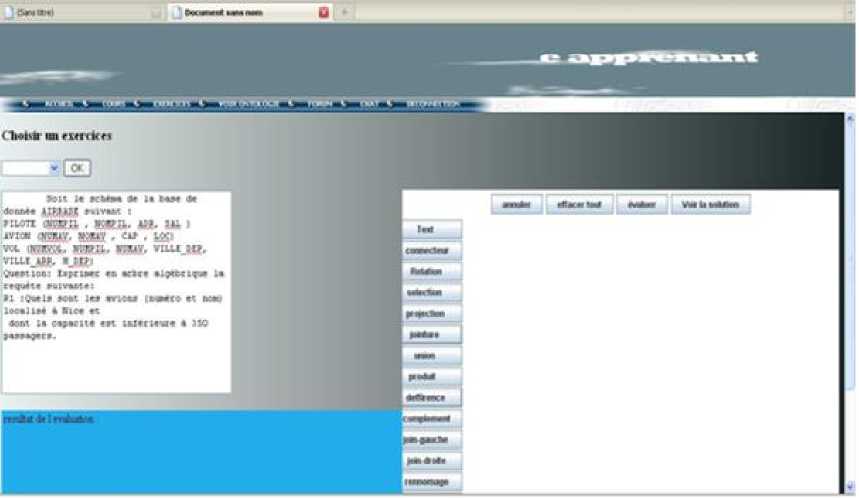
  Fig. 1. The learner’s space for query resolution using an algebraic trees editor

  
  
  

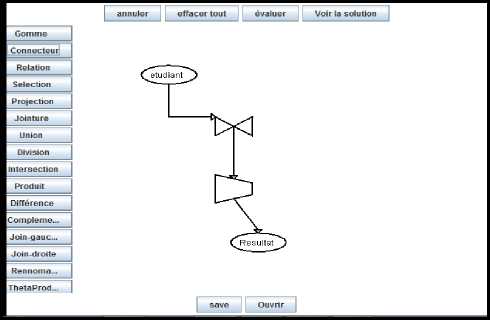
  Fig. 2. The algebraic trees editor.

  
  

• B.    Semantic Analysis of Algebraic Trees

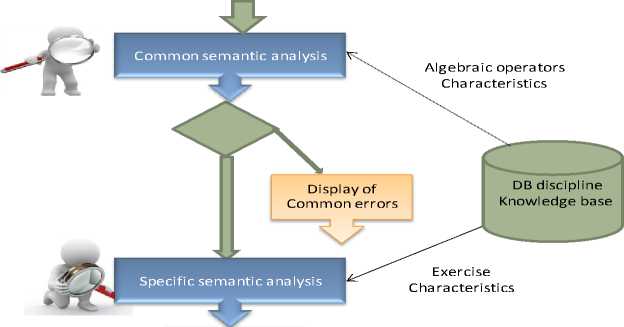
After building an algebraic tree to answer an open question, the learner can click on the button “evaluer” to automatically evaluate his/her solution. The display of the error diagnosis result is also done via the editor in a reserved zone. The semantic analysis process, as it is defined in ODALA approach is divided into two main steps (see “Fig. 3”): the common semantic analysis and the specific semantic one.

The algebraic tree built by a learner

Display of Specific errors

Fig. 3. The semantic analyzer

• 1.    Common semantic analysis

• 2.    Specific semantic analysis

The common semantic analysis is based on the characteristics of the RDB discipline concepts defined in the knowledge base generated from the domain ontology Onto-TDM. A common semantic error is generally independent from the exercise statement and is a logical bad use of an algebraic operator. For example we have: “Unary operator connected to two relations”, “more than two relations for an operator”, “selection operator without condition”, “binary operator with only one input relation” (see “Fig. 4”) …

The specific semantic analysis uses the exercise characteristics. The errors thus detected will be specific to the current exercise statement and are useful to check in general if the response given is correct according to the displayed query in the exercise. Currently, in our tool, we check mainly if the learner has used in his/her tree the adequate combination of algebraic operators on one hand and the relations and attributes names of the current exercise database on the other. For example, we have these specific semantic errors, from the error database of the tool: “the difference operator is unplanned in the exercise solution”, “the relation named ‘Student’ is an incorrect input”, and “At least, one selection operator is requested in the tree” …

“Fig. 5”, for example, shows a specific semantic error: “error about the selection condition LOC=Paris”, where the town name, which is the selection criteria, given in the question is Nice and not Paris. This error is the result of the specific analysis of the tree displayed in the left window (built by a learner of our university) as a solution for the exercise shown in the top window.

The semantic analyzer proceeds in two successive phases: common semantic analysis and if there are no common semantic errors, schedules with a specific semantic analysis that looks for specific semantic errors. The effectiveness of the semantic analyzer is related to the completeness of errors base and the defined rules for exercises’ characteristics management in the discipline knowledge base. In the end, this semantic analysis process remains a heuristic and has to be improved in an incremental way with its use in real classes. The interesting with such tools based on errors diagnosis is the help provided to novice students and their teachers to avoid already known errors.

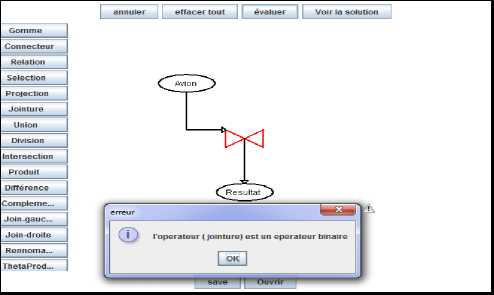
Fig. 4: Display of a common semantic error

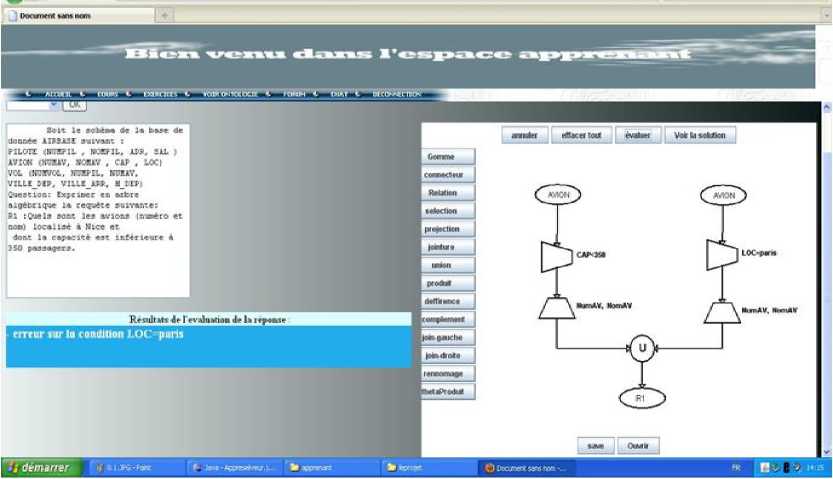
Fig. 5: Display of a specific semantic analysis results

• IV. Evaluation Of Our Proposals

First the editor prototype was tested with a set of data chosen to verify the quality of the application in editing and analyzing algebraic trees. The weaknesses detected for the edition module, that are currently under improvement, concern the possible erase of only one drawn operator and the zoom possibility for the drawn forms. For the analysis, the known errors are well detected. As expected, the unknown errors (not recorded in the errors’ base) are not detected.

On the other hand, the prototype was experimented with real students from the second year license in academic computer science from our university. The tool was successively proposed to hundred and twenty (120) student for the 2011-2012 academic year and for three hundred and eighty (380) for the 2012-2013 academic year. We first gave a presentation to all the students to explain the tool features, after that we proposed for them to try it in practical rooms where the tool is installed. After that we collected their responses to the following question:

“ Do you enjoy the tool and do you think it can help you learn relational databases ?”

We collected for the first academic year hundred (100) responses from hundred and twenty (120) students asked and for the second year, we got two hundred and ninety five (295) responses from three hundred and eighty asked.

Table 1 gives the summary of the students’ responses analysis where we can see that most of them enjoyed the editor and thought that it could help them particularly in the beginning of queries resolution.

Table 1. Students’ responses analysis about the proposed tool

	2011-2012 (100 responses)	2012-2013 (295 responses)
Yes	85%	90%
No	10%	2%
Without opinion	5%	8%

For the “yes” line of table 1, we noticed that there is an increase of interest in the first academic year compared to the second one. We think that this can be explained by the fact that the students number has doubled in the second year.

The two main arguments collected from the students that gave the “no” response” are:

• •    “I have to spend time to learn about the tool. I prefer read documents to learn how to write queries with algebraic trees formalism”.

• •    “I don’t believe in ‘conceptual’ languages. I prefer use directly SQL, so that i will have the query execution”.

In the third and last step of the editor evaluation, we collected the RDB teachers’ opinions about the possible use of the tool for self learning to enhance RDB teaching.

The ten (10) teachers (involved in courses, guided works or practical works) from our department agreed that the tool can be very helpful for them even if the errors base isn’t complete particularly with beginners in large groups, specific need students and those in difficulty.

• V. Conclusion

This tool was tested with a set of data and with real students and teachers of our university. The results of the experiments showed that the tool can be very helpful for novice students and others in specific needs or in difficulty. The teachers also were interested by the tool especially to handle large groups and/or students with obstacles in learning and/or delay. In general, this tool can also enhance blended learning approaches and disciplinarians’ didactics. In addition, the graphic editor helps the students to avoid mixing between form errors and semantic ones.

As perspectives, we have in one hand technical ones to improve some editing options and organize a second prototype as a complete web service. In the other hand we have research perspectives where we plan first to study the impact of the tool on the learning results of students and after that to define a blended pedagogy to integrate the use of the tool in relational databases teaching for beginners.